三重混合范数的L型嵌套阵列二维角度估计

陈 璐， 毕大平,2, 潘继飞(.国防科技大学电子对抗学院,合肥 230037；

2. 安徽省电子制约技术重点实验室，合肥 230037)

0 引 言

角度估计(Direction of arrival，DOA)是阵列信号处理中一个基本问题，广泛应用于雷达、声呐、无线通信等领域。为了克服一维DOA估计在实际应用中的局限性，二维(Two-dimensional，2D)角度估计受到广泛关注和研究[1]。嵌套阵列是近来提出的一种新型阵列结构[2-3]，通过对阵元位置的合理分配，可以达到扩展参数估计自由度的目的[4-5]，而对于嵌套阵列二维角度估计的研究较少[6]，本文主要针对这一问题进行研究。

可用于二维DOA估计的常规阵列有：面阵[7]、平行阵[8]、L型阵[9]。文献[10]证明L型阵的DOA估计性能要优于其它几种阵型，因此关于2-D DOA估计的许多研究均基于L型阵。

二维角度估计算法中，主要分为三类：第一类为基于子空间类空间谱估计算法，例如:MUSIC，ESPRIT，PM等算法；对于L型阵2-D DOA估计问题，文献[11]提出一种有效的传播算子方法(Propagator method, PM)，但这种方法无法实现俯仰角和方向角的自动匹配，造成两个维度角度的配对容易出现错误。为解决L型阵2-D角度的自动配对问题，文献[12]利用互协方差矩阵实现2-D DOA估计和角度自动配对，但在低信噪比和小快拍数条件下，容易出现虚假角度，影响了DOA估计的性能。为减少DOA估计算法受信噪比的影响，文献[13]提出了一种基于互协方差矩阵的联合奇异值分解算法(Joint singular value decomposition，JSVD)，该算法在信噪比较低的条件下，仍然具有较好的测向性能，并且能够实现2-D角度的自动配对，然而，算法需要进行大量的矩阵SVD运算和空间谱搜索运算，计算复杂度较高。文献[14]提出了一种基于PM算法和旋转不变子空间技术(Estimating signal parameters via rotational invariance techniques, ESPRIT)的2-D DOA估计算法，该算法利用L型阵上两个均匀阵的共轭对称性，有效扩展了阵列孔径，避免了繁琐的峰值搜索过程，算法角度估计精度高且计算复杂度低。

第二类是基于参数化的空间谱估计方法，例如最大似然估计算法、加权子空间拟合算法，高阶累积量算法。文献[15]提出了一种基于信号协方差矩阵的2-D角度配对算法，该算法构造了一个基于两个信号协方差矩阵的目标函数，通过引入一个置换矩阵达到2-D角度的最优配对。文献[16]将L型阵的单个维度上的均匀阵列划分成两个重叠子阵，计算两子阵的互协方差矩阵，通过将协方差矩阵和它的转置相加，对得到的矩阵进行分割和线性运算，分别估计出两个维度的角度，算法的缺点是两个维度角度无法自动配对。文献[17]提出了一种基于高阶累积量的2-D L型嵌套阵列DOA估计算法，使用2维平滑方法,恢复其偶数(2q)阶累积量矩阵的秩，采用2维MUSIC算法，进行方位角和俯仰角的估计。算法具有更好的测向精度，但需要信号采样数较多，当采样数不足时，将影响算法的测向数度。

针对2-D DOA估计中的互耦问题，文献[18]提出了一种互耦系数估计的2-D矩形阵DOA估计算法，算法建立了矩形阵互耦测向模型，利用秩缩减方法同时估计互耦系数矩阵和2-D角度，在存在阵元互耦效应的条件下，比传统2-D DOA估计算法精度更高。

第三类为基于压缩感知类空间谱估计算法。近年来，压缩感知理论被用于角度估计，但在二维测向中存在计算复杂度高的问题，特别是嵌套阵列对应的差分共阵虚拟阵元数较多，导致压缩感知理论中的字典矩阵维数较高，计算复杂度大。文献[19]提出一种解决互耦条件下的二维角度估计算法，算法通过连续网格细化技术减小压缩感知求解过程的计算量，算法通过构造两个稀疏字典，顺序估计两个维度角，但是由于二个维度角估计是一个联合估计的耦合问题，因此算法的角度估计为有偏估计[20]。文献[21]提出一种分离稀疏表示DOA算法，该算法构造了两个稀疏字典，通过交替最小化算法求解该凸优化问题，但算法仅适用于单测量矢量情况，当存在多矢量情况时，算法复杂度较高[22]。

为降低L型嵌套阵利用压缩感知算法时的计算复杂度，本文提出了一种三重混合范数稀疏重构算法，首先建立了俯仰角和方位角可分离的2-D测向模型，然后将两个维度的嵌套阵数据分块，建立基于联合协方差矩阵稀疏的二维角度估计模型，为减小计算复杂度，将模型转化为三重混合范数块稀疏模型，利用交叉迭代的方法计算最优解，得到二维角度估计值，并且两个维度可以自动配对。仿真显示，本文算法具有良好的估计精度和角度分辨率。

1 L型嵌套阵二维测向模型

嵌套阵列是由若干个间隔不同的均匀阵列组合而成的非均匀线阵，通过数据处理能够有效地提高阵列自由度。M级嵌套阵列结构如图1所示，M级子阵的阵元数目分别为N1,N2,…,NM，阵元间隔分别为d1,d2,…,dM，满足dm+1=(Nm+1)dm，其阵列自由度为可表示为：

(1)

其中，Ni为第i级嵌套子阵的阵元数。可以看出，嵌套阵列能够估计的辐射源角度数目远远大于其物理阵元数。

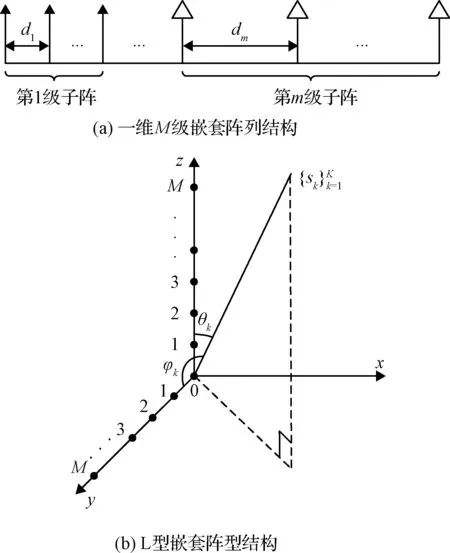
图1 一维和二维嵌套阵列模型Fig.1 One and two dimensional nested array model

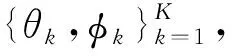
(2)

(3)

Y=AY(φ)S+NY

(4)

Z=AZ(θ)S+NZ

(5)

其中，Y=[y(t1),y(t2),…,y(tT)]，Z=[z(t1),z(t2),…,z(tT)]，AY(φ)=[aY(φ1),aY(φ2),…,aY(φK)]，AZ(θ)=[aZ(θ1),aZ(θ2),…,aZ(θK)]，S=[s(t1),s(t2),…,s(tT)]，NY=[nY(t1),nY(t2),…,nY(tT)]，NZ=[nZ(t1),nZ(t2),…,nZ(tT)]。y轴和z轴方向嵌套阵观测数据互协方差矩阵可表示为

(6)

(7)

(8)

(9)

(10)

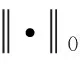
(11)

(12)

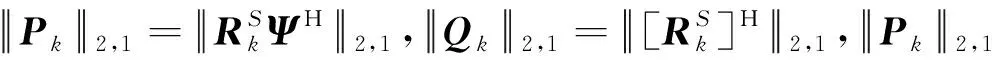
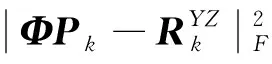
(13)

2 三重范数稀疏重构模型

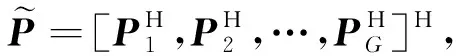
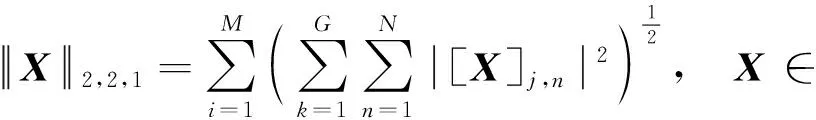
(14)

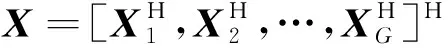
(15)

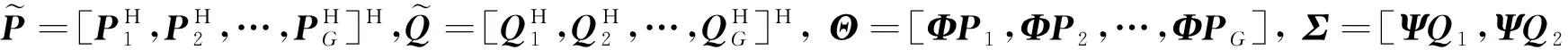
(16)

固定变量P可得

(17)

3 交叉迭代求解

式(16)的梯度可以表示为

(18)

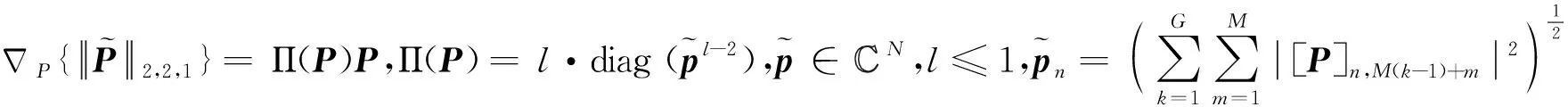
Π(P)P+γ1(ΦHΦP-ΦHRYZ)+

γ2(P-ΣH)=0

(19)

P的解为

P=(Π(P)+γ1ΦHΦ+γ2I)*(ΦHRYZ+γ2ΣH)

(20)

其中,(·)*表示矩阵伪逆。式(17)的梯度可以表示为

(21)

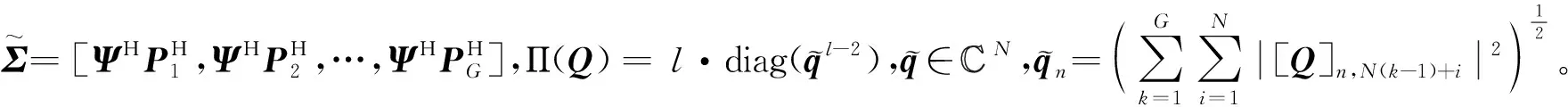
(22)

Q的解为

(23)

式(20)、(23)为式(16)、(17)的闭式解，变量P，Q的迭代如下所示

P(j+1)= (Π(P(j))+γ1ΦHΦ+γ2I)*·

(ΦHRYZ+γ2Σ(j)H)

(24)

(25)

4 仿真校验

假设空间存在12个不相关窄带辐射源角度(如表1)，使用本文提出的三重混合范数估计辐射源角度，稀疏字典的角度间隔为0.5°，L型嵌套

阵列为2级嵌套，每一级阵元数为5。采用均方差的方法(Root mean square error, RMSE)估计角度误差

(26)

表1 辐射源角度Tabel 1 Radiant source angles

图2给出了本文算法的角度估计结果，图2(a)为立体图形，图2(b)为平面图形，从图2可以看出，利用本文提出的2维角度估计算法，可以估计出12个辐射源的2维角度，两个维度角度为自动配对，并且有较高的角度分辨率。由于嵌套阵列的数据具有较大的虚拟孔径，因此，可以估计的辐射源目标数大于阵元个数，并且角度估计精度较高。

图2 本文算法2D角度估计结果Fig.2 2D angle estimation results of the proposed algorithm

图3为12个辐射源50次蒙特卡罗试验得到的2维角度估计值散布图。圆圈代表辐射源2维角度真实位置，圆点代表每次试验的角度估计值，由图3可知，本文提出的算法估计值大部分落于真实值附近，说明算法具有良好的稳定性。(41°,66°) (41°,70°)两角度距离较近，但是本文算法仍然能够将其分离，说明算法具有较好的分辨率。

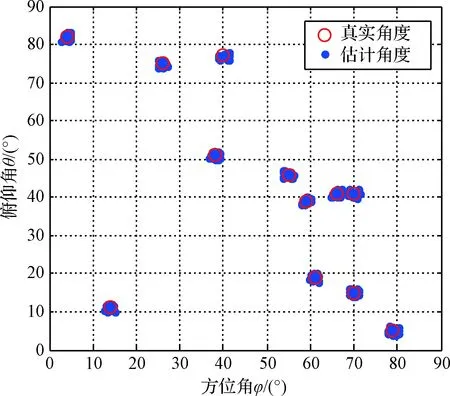
图3 50次蒙特卡罗试验角度估计值散布图Fig.3 Scatter diagram of 50 Monte Carlo experimental angle estimation results

图4不同分集数G条件下，算法运算时间和算法角度估计精度的仿真结果，从图4(a)可以看出，当分集数G增加时，算法的运算时间不断增加，说明算法运算复杂度不断提高。从图4(b)可以看出，当分集数G增加时算法的角度估计精度在不断提高，分集数增加到一定程度时，算法精度提高变慢。因此，分集数G的选择需要兼顾算法复杂度和算法精度。

图4 不同分集数G对算法的影响Fig.4 The influence of different diversity number G on the algorithm

当快拍数为2000时，在不同信噪比条件下，对3个辐射源角度(11°,14°)，(75°,26°)，(51°,38°)进行估计，算法中将数据分为G=10份，构成块稀疏矩阵，500次蒙特卡罗试验得到图5(a)结果。与文献[11,13-14]中的算法进行比较可知，当信噪比SNR<0 dB时，本文算法角度估计精度明显高于其他三种算法。当信噪比0 dB ≤SNR<10 dB时，本文算法角度估计精度略高于其它三种算法。当SNR≥10 dB时，四种算法精度相近。这是因为信号子空间搜索类算法易受噪声影响，信噪比低时，噪声子空间将会污染信号子空间，导致搜索失败。而本文提出的基于压缩感知的混合范数二维角度估计算法不存在这一问题，可以在信噪比较低的条件下，实现高精度角度估计。

当信噪比为20 dB时，在不同快拍数条件下，对3个辐射源角度(11°,14°)，(75°,26°)，(51°,38°)进行估计，算法中将数据分为G=10份，构成块稀疏矩阵，500次蒙特卡罗试验得到图5(b)结果。由图5(b)可知，在低采样点数条件下，本文算法精度要高于其它三种算法，这是因为其它三种算法在计算时，取全局采样点协方差矩阵的均值作为观测值的协方差矩阵，而本文算法将采样点分成若干份，分别进行参数信息提取，因此算法精度要高于其它三种算法。

当信噪比为20 dB，快拍数为500时，对不同个数辐射源进行角度估计，500次蒙特卡罗试验得到图5(c)结果。与三种算法比较可以看出，本文算法角度估计数度较高。这是因为本文算法利用压缩感知理论，只要满足稀疏性，估计目标个数对算法影响较小。而子空间搜索类算法，对多个目标进行搜索的效果较差。

图5(d)为不同快拍数条件下，几种算法的运算时间对比，由图5(d)可知，在相同快拍数条件下，本文提出算法的运算时间要高于文献[11]和文献[13]，低于文献[14]。说明本文算法的算法复杂度高于文献[11]和文献[13]，低于文献[14]。

5 结 论

对于L型嵌套阵列二维测向问题，本文提出了一种基于三重混合范数的二维测向算法，首先构造了y轴和z轴可分离的L型嵌套阵列二维测向模型，将两个方向上的数据采样点均分为G份，计算每一份采样点的互协方差矩阵，将二维角度估计问题转化为基于互协方差矩阵稀疏化的优化问题，建立了三重混合范数的稀疏重构模型，利用交叉迭代的方法进行求解。试验仿真表明，三重混合范数稀疏重构算法能够有效估计出辐射源的二维角度，并且能够实现自动配对，具有较高的分辨率和鲁棒性。与其它算法相比，三重混合范数稀疏重构算法在低信噪比、低快拍数条件下，性能均优于其它算法，并且当辐射源数目较多时，算法仍有较好的角度估计精度。如何将算法应用于宽带角度估计问题中是下一步研究的重点。

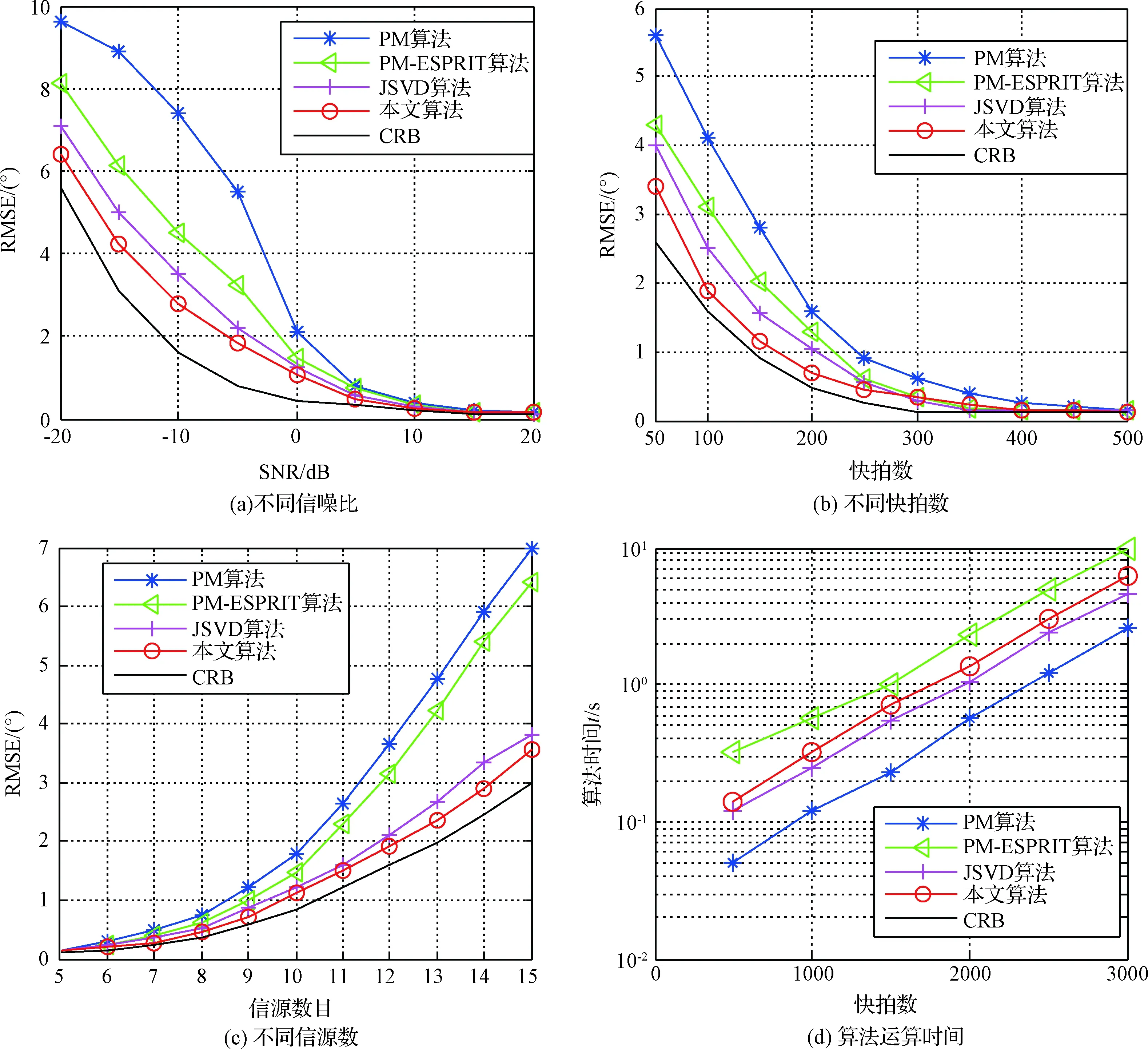
图5 算法性能对比Fig.5 Algorithm performance comparison