空间太阳能电站的准对日定向姿态
2019-02-15李庆军邓子辰王嘉琪
李庆军,邓子辰,王 艳,王嘉琪
(西北工业大学工程力学系,西安 710072)
0 引 言
太阳能是一种丰富的清洁可再生能源,太阳能的合理利用对解决能源与环境问题有着重要的意义[1]。1968年美国学者Glaser首次提出了空间太阳能电站的概念,通过在太空运行的大型太阳能电池阵列产生电能,并通过无线传输的方式将电能传输到地面[2]。空间太阳能电站的概念首先得到了美国国家航空航天局和能源部的重视,他们率先开展了空间太阳能电站的概念设计和评估,并提出了首个5 GW级的空间太阳能电站设计方案:1979空间太阳能电站基准系统[3]。到目前为止世界各国已经提出了二十多个空间太阳能电站的设计方案,包括太阳帆塔[4]、圆柱型空间太阳能电站[5]、绳系空间太阳能电站[6]、Abacus空间太阳能电站[7]和多旋转关节空间太阳能电站[8]等。
与普通的航天器相比,空间太阳能电站具有质量超大、结构尺寸超大、面质比超大、结构超柔等特点,使得空间太阳能电站表现出与普通航天器不同的动力学行为。空间太阳能电站在太空中受到多种轨道和姿态摄动因素的影响,包括地球非球形摄动、万有引力梯度力矩摄动、太阳光压摄动、日月引力摄动、微波反作用等[9-10]。在这些摄动因素的作用下,空间太阳能电站会偏离原轨道和姿态,影响系统的正常工作。由于空间太阳能电站尺寸和质量都超大,轨道和姿态的维持需要消耗大量的控制燃料和能量,从而提高了运行成本。在轨道保持方面,有研究者尝试将空间太阳能电站置于地球同步拉普拉斯轨道,使地球非球形摄动和日月引力摄动造成的影响相互抵消,从而每年节省约36453 kg的控制燃料[9,11]。
在姿态方面,最简单的姿态方案是采用万有引力梯度稳定的姿态,如太阳帆塔、绳系空间太阳能电站等的姿态[12]。这种姿态方案在万有引力梯度的作用下自动保持稳定[13],在不考虑其他摄动力矩的情况下只需很小的控制力矩维持。然而这种姿态方案的太阳能电池阵列无法保持对日定向,因而无法实现持续发电,而且平均发电效率低、需要在两面安装太阳能电池板[14]、太阳能电池板的利用率低,从而限制了这种姿态方式的应用。为了克服万有引力梯度稳定姿态方案的缺点,很多空间太阳能电站采用对日定向姿态方案(如1979空间太阳能电站基准系统、Abacus空间太阳能电站和多旋转关节空间太阳能电站),即对太阳能电池阵列施加姿态控制力矩,从而保持电池阵列对日指向。对日定向姿态方案需要提供随时间呈正弦曲线变化的姿态控制力矩,对于Abacus这种超大的空间太阳能电站而言,需要提供很大的控制力矩(峰值为143000 N·m),如果采用动量交换的方式进行姿态控制,则需要采用十万个控制力矩陀螺,使工程实现成为困难[10]。为了解决这个问题,Wie等[10]提出了采用离子推进器的控制方法,并设计了低带宽的前馈-反馈控制器。为了实现太阳能电池阵列对日定向的高精度姿态控制,Wu等[15]设计了时变鲁棒最优控制器,采用干扰抑制和线性二次型最优控制相结合的办法,实现了对Abacus空间太阳能电站的高精度对日指向。Li等[16]针对姿态摄动因素随时间呈周期性变化的特点,设计了基于双曲正切切换的迭代学习控制方法,在考虑传感器噪声、空间姿态摄动、转动惯量不确定性和目标轨迹慢时变的情况下进行数值仿真,提高了姿态控制精度的同时降低了对噪声的敏感性。虽然上述的姿态控制方法能达到较好的控制精度,但对于大型的太阳能电池阵列仍然需要提供较大的姿态控制力矩。
为了避免对日定向姿态所带来的巨大姿态控制力矩问题,研究者们尝试提出新的空间太阳能电站概念。美国提出了太阳盘空间太阳能电站,通过太阳盘的自转保持太阳能电池阵列对日定向[17-18]。另外美国提出的圆柱型空间太阳能电站[5]和西安电子科技大学提出的具有球形反射镜的SSPS-OMEGA方案[19-21],由于结构具有对称性,降低了万有引力梯度力矩的影响。钱学森空间技术实验室提出了多旋转关节空间太阳能电站,将大型的太阳能电池阵列用多个较小的太阳能电池子阵代替,并将太阳能电池子阵沿南北方向排列,从而大大降低了每一个子阵所需的姿态控制力矩(峰值仅为12 N·m左右)[16]。除了在概念方案设计上改进外,另外一种解决办法是从姿态方案本身提出改进,从而放松对概念方案设计的要求。Elrod[22]提出了一种不需要控制就能使航天器保持在某个方向附近振动的准惯性定向姿态方案。如果空间太阳能电站采用准惯性定向姿态方案,通过选择合适的姿态初始条件,在无控的情况下太阳能电池阵列可以在空间中某个固定的方向(本文称为主方向)附近作小幅度振动,主方向可以是轨道平面内的任一方向。然而文献[22]中提出的概念认为主方向是固定不变的,而实际上太阳的方向在地心惯性坐标系中是缓慢变化的。Sincarsin在准惯性定向姿态的基础上进一步考虑了太阳方向的缓慢变化,并将这种姿态称为准对日定向姿态[23]。
本文在文献[23]的基础上研究准对日定向姿态方案,为空间太阳能电站的太阳能电池阵列提供一种可选的姿态方案。本文第1节和第2节通过一个简化的姿态动力学模型阐述了准对日定向姿态的概念,给出了准对日定向姿态构造的数值方法,并从发电效率和所需姿态控制燃料两方面对比了对日定向姿态和准对日定向姿态。第3节设计了姿态控制器,使太阳能电池阵列在任意姿态初始条件下收敛到准对日定向姿态。第4节进一步考虑了系统的轨道运动、偏航和滚转运动、结构振动对准对日定向姿态的影响。最后一节总结了本文研究得到的结论。
1 简化的姿态动力学模型
空间太阳能电站的姿态动力学与控制主要关注太阳能电池阵列的对日指向和微波发射天线的对地指向。本文旨在提出一种太阳能电池阵列的对日指向俯仰运动姿态方案,因而暂不考虑微波发射天线的对地指向问题。为了简化动力学分析过程,本文只考虑万有引力梯度力矩的影响,而忽略轨道摄动力和其他姿态摄动力矩。
太阳能电池阵列的长度一般比厚度大两个数量级,且在姿态受控的情况下滚转角和偏航角近似为零。基于上述假设,太阳能电池阵列可以简化为质量均匀分布的线型刚体,如图1所示。惯性坐标系的坐标原点位于地球的质心,OXY平面为轨道平面。为了给出准对日定向姿态方案的统一描述,OY轴指向初始时刻的太阳在OXY平面的投影。在此简化模型中,太阳能电池阵列的轨道由轨道半径r和角度θ描述,姿态由俯仰姿态角α描述。

图1 太阳能电池阵列的刚性模型Fig.1 Rigid model of solar arrays
采用Hamilton原理建立系统的动力学方程,取系统的广义坐标为q=[r,θ,α]T,系统的动能可表示为随质心平动的动能和绕质心转动的动能之和:
(1)
其中,m为刚体的质量,l为刚体的长度。根据文献[24],系统的势能为:
(2)
其中,μ=3.986×1014m3·s-2为地球引力常数。为了对系统进行降阶处理,引入系统的广义动量[25]:
(3)

(4)
根据Hamilton原理,系统的Hamilton动力学方程为[25]:
(5)
其中,Q为广义力,可通过虚功原理求得。当系统受到姿态控制力矩M的作用时,将式(1)~式(4)代入方程(5),得到系统的动力学方程为:
(6)
由方程(6)可知,太阳能电池阵列所受的万有引力梯度力矩的表达式为:
(7)

2 准对日定向姿态方案
本节给出准对日定向姿态的概念、数值构造方法以及对日定向姿态和准对日定向姿态的比较。在本节的研究中,空间太阳能电站的初始轨道条件是地球静止轨道,系统的质心位于OX轴的正方向。
2.1 其他俯仰姿态方案

对于万有引力梯度稳定姿态,姿态角按如下规律变化:
α=0,γ=θ=ωGEOt
(8)
其中,ωGEO为地球静止轨道的轨道角速度,由式(7)可知,万有引力梯度力矩Tg恒为零。此时刚体的一端始终指向地心,刚体在万有引力梯度力矩的作用下处于稳定的平衡状态[13]。这种方案稳定性好、易于保持,但太阳能电池阵列没有保持面向太阳,因此无法持续供电,发电效率低,需要在太阳能电池阵列的两面安装太阳能电池板,太阳能电池板也没有得到充分利用。
为了避免上述问题,可以采用对日定向姿态方案,对太阳能电池阵列施加姿态控制力矩,从而使其保持垂直于太阳光方向在轨道平面的投影。由于太阳初始时刻位于Y轴的正方向,从地球指向太阳在轨道平面的投影的单位向量可由下式计算:
vSun=[-sin(ωSunt),cos(ωSunt)]T
(9)
其中,ωSun为地球绕太阳公转的角速度。对日定向姿态方案的姿态角变化规律为:
(10)
由式(7)可知,姿态控制力矩随时间呈正弦规律变化,幅值与系统的转动惯量成正比。因此对于大型的太阳能电池阵列,需要消耗较多的控制燃料。
2.2 准对日定向姿态的概念
为了降低姿态控制燃料的消耗,同时使航天器有一定的指向能力,Elrod提出了准惯性定向的姿态方案[22]。他的方案不考虑太阳方向随时间的变化,即太阳一直位于Y轴正方向,为了节省姿态控制能量,方程(6)中的控制力矩M取为零。为了更清楚地阐述准惯性定向姿态,取初始条件为
(11)
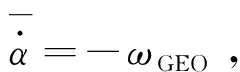

图2 α的相图Fig.2 Phase diagram of α

图3 α随时间的变化Fig.3 Dynamic response of α
图4给出了准惯性定向姿态的相图,由图4可知,γ作周期振动,振幅约为±0.328 rad,γ的平均角度方向称为主方向,图4所示的主方向为γP=0。为了更清晰地表示三种姿态方案的区别,图5给出了这三种姿态方案的示意图。

图4 准惯性定向姿态的相图Fig.4 Phase diagram of quasi-inertial oriented attitude
Elrod提出准惯性定向姿态的概念时,没有考虑主方向需要随时间变化的情形。而太阳在惯性坐标系XOY中的方向是按式(9)缓慢变化的,因此太阳能电池阵列的主方向需要跟随太阳方向的变化,即采用Sincarsin提出的准对日定向姿态。对于运行在地球静止轨道的空间太阳能电站而言,不考虑太阳方向的变化时,主方向应为γP=0,一个准惯性定向姿态的周期应为一个轨道周期,即一个恒星日,且周期末时刻的γ和v值与周期初始时刻均相同,即:
γ(t=23×3600+56×60+4)=γ0=0
(12)
v(t=23×3600+56×60+4)=v0=vQI
(13)
式中:vQI为常数。当考虑太阳方向的改变时,主方向应为γPS=ωSunt,准对日定向姿态的一个周期应为一个太阳日,且周期末时刻的v与周期初始时刻相同,周期末时刻的γ值与γPS的值相同,表示为:
(14)
v(t=24×3600)=v0=vQIS
(15)
式中:vQIS为常数。
2.3 准对日定向姿态的数值构造

定义周期末的姿态误差为
E=γ(t=24×3600)-24×3600×ωSun
(16)
通过选择不同的v0,得到不同的E值,从而形成了从v0到E的映射E=f(v0),其图像如图6所示。图中的不连续点是由于当v0从小到大经过该点时,姿态角α从翻滚的状态变成了摆动的状态[13],从而产生了姿态误差的不连续。从图6可以看出,曲线在较大的v0范围内与横轴只有一个交点,因此可以采用二分法求解映射E=f(v0)的零点,从而得到vQIS的准确数值。为了提高收敛速度,也可以在较小的范围内采用弦割法。本文采用弦割法得到的初值约为vQIS=-0.7871676ωGEO,准对日定向姿态的γ响应如图7所示。同理可求得的准惯性定向姿态初值为vQI=-0.7879522ωGEO。

图6 不同v0下的周期末姿态误差Fig.6 Attitude errors at the end of a period versus v0

图7 准对日定向姿态的γ时间响应曲线Fig.7 Time history of γ for quasi-Sun-pointing attitude
2.4 太阳光的捕捉率与姿态控制燃料比较
万有引力梯度稳定姿态方案、对日定向姿态方案和准对日定向姿态方案的不同之处主要有两方面:第一是太阳光的捕捉率η不同,在本文中定义为垂直于太阳光方向的太阳能电池阵列面积与太阳能电池阵列面积之比;第二是控制力矩不同。在春分或秋分的一天时间内,太阳可认为位于轨道平面内,三种姿态方案的η随时间变化规律如图8所示。从图8可以看出,对日定向姿态方案的太阳光捕捉率恒为1;万有引力梯度稳定姿态的太阳光捕捉率按余弦函数的绝对值变化,在一天内从一两次变为0,再变为1,均值为0.637;而准对日定向姿态的太阳光捕捉率在1附近作小幅度振动,最小值为0.947,均值为0.973。值得注意的是,在万有引力梯度稳定方案中的太阳能电池阵列需要在正反两面都安装太阳能电池板,否则发电效率减半,而对日定向和准对日定向姿态方案中的太阳能电池阵列只需在一面安装太阳能电池板,因而太阳能电池板的利用率较高。如果不是春分或秋分,由于太阳能电池阵列垂直于赤道平面,所以只能捕捉到太阳光在赤道平面的分量,即图8中所有点的数值应乘以太阳赤纬的余弦值。在以下分析中只考虑春分或秋分的情况。

图8 三种姿态方案的太阳光捕捉率(春分或秋分)Fig.8 Ratios of captured area of solar radiation to area of solar arrays (at equinoxes)

(17)
该力矩可采用一对力偶来提供,则每一个力的大小的变化规律应为
F=|Tg/3200|
(18)

(19)
因而一年内消耗的燃料约为36791 kg。
3 准对日定向姿态控制
虽然准对日定向姿态通过自身的运动避免了万有引力梯度力矩的影响,但初始时刻的微小误差会随时间放大,因此需要对太阳能电池阵列的准对日定向姿态进行控制。
3.1 控制器设计
为了使太阳能电池阵列在初始姿态误差条件下收敛到准对日定向姿态,并保持姿态的稳定性,本文设计比例-微分控制器进行姿态控制。控制误差定义为
e=α-α*
(20)
式中:α*是准对日定向姿态的姿态角。虽然α*没有解析表达式,但可以通过数值方法得到α*在每一时刻的值。另外也可以对α*在每一时刻的值进行快速傅里叶变换,从而用截断的傅里叶级数近似地表示α*,这样做的优点是可以对α*进行求导数或积分等理论运算。控制力矩表达式如下:
(21)

(22)
式中:ωc为控制器的带宽,ζ=0.7为控制器的阻尼比。数值仿真中将给出不同的控制器带宽的控制效果。
3.2 控制效果数值仿真


图9 控制误差Fig.9 Control error

图10 控制力矩Fig.10 Control moment

图11 不同初始条件下的γs相图Fig.11 Phase diagram of γs for different initial conditions

4 航天器运动对准对日定向姿态的影响
本节在前文的研究基础上,进一步研究系统的轨道运动、偏航姿态运动、滚转姿态运动和结构振动对准对日定向姿态的影响规律。
4.1 轨道运动的影响


图12 不同控制带宽的控制器收敛区域Fig.12 Convergence domains of the controller for different bandwidths

图13 轨道离心率对准惯性定向姿态初值的影响Fig.13 Effect of orbital eccentricity on initial condition of quasi-inertial oriented attitude

图14 椭圆轨道下准惯性定向姿态的相图Fig.14 Phase diagram of quasi-inertial oriented attitude in elliptic orbits
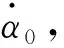

图15 椭圆轨道下的γs相图Fig.15 Phase diagram of γs in an elliptic orbit
接下来研究圆形轨道下轨道半径对准对日定向姿态的影响。在圆形轨道假设条件下,动力学方程(6)可简化为:
(23)
将上述动力学方程的自变量变换为θ=ωt,得:
(24)
式中:上标两撇代表对θ求二阶导数。由方程(24)可知,α随着θ的变化规律跟轨道半径(轨道角速度)无关,从而可以判断在不同轨道半径的圆形轨道,都存在准惯性定向姿态和准对日定向姿态。准惯性定向姿态的初始条件与地球静止轨道上的情况相同。
4.2 偏航和滚转的影响
空间太阳能电站在轨运行时,需要对太阳能电池阵列进行姿态控制,以保持其姿态指向精度。在此情形下,可以认为偏航运动、滚转运动的角度以及相应的角速度与俯仰运动相比都是小量。在地球质心建立惯性坐标系OXYZ,其中OZ轴与轨道平面垂直,OY轴指向初始时刻的太阳在OXY平面的投影。将太阳能电池阵列近似看作长方体,oxyz为惯性主轴坐标系,采用z-y-x顺序的欧拉角对太阳能电池阵列进行姿态动力学建模,分别表示为φ,θ和ψ,如图16所示。

图16 太阳能电池阵列的三维简化模型Fig.16 Three dimensional simplified model for a solar array
姿态运动学方程和动力学方程分别为[26]
(25)
(26)
式中:c和s分别代表cos和sin。式(26)中的Tg=[Tgx,Tgy,Tgz]T为万有引力梯度力矩[26]
Tg=3ω2n×(In)
(27)
式中:I为惯量矩阵,n=[nx,ny,nz]T为从卫星指向地心的单位矢量,可由下式计算
n=A[-cocωt,-sinωt,0]T
(28)
式中:A为姿态矩阵。
当θ,ψ,ωx和ωy均为小量时,可将sinθ和sinψ分别用θ和ψ代替,cosθ和cosψ均用1代替,且忽略小量相乘的项,则俯仰姿态的动力学方程可从上述三维的姿态动力学方程中解耦出来:
(29)
式中:φ即为二维简化模型里的γ,因此φ-ωt可看作是α。通过将三维的姿态动力学方程忽略高阶项,得到解耦的俯仰姿态动力学方程,这说明太阳能电池阵列的偏航和滚转运动对俯仰运动的影响都是高阶小量,在姿态受控的情况下可以忽略。
为了进一步简化方程(29),设δ=(Iy-Ix)/Iz,对于如图16所示长、宽、高分别为l,w,h的太阳能电池阵列,有
(30)
当w/l的值变化时,δ的变化如图17所示。由于太阳能电池阵列的w通常比l小一两个数量级,因此δ约为1。从而方程(29)可进一步化简为方程(23),这说明了本文将太阳能电池阵列看作线型刚体的假设是有效的。由图17可知,对于普通的卫星,三个方向的转动惯量比较接近,因此δ非常小,从而俯仰姿态受到万有引力梯度力矩的影响也比较小。

图17 δ的变化规律Fig.17 Variation of δ
4.3 结构振动的影响

图18给出了柔性梁的控制误差图,由图18可知,对日定向姿态的姿态误差最大约为0.5°,而准对日定向姿态的误差比对日定向姿态小一个数量级。图19给出了梁的控制力矩,对日定向姿态需要的控制力矩最大值约为12 N·m,而准对日定向姿态的最大控制力矩仅为0.08 N·m。对日定向姿态的控制误差和控制力矩均按三角函数的规律变化。在轨运行过程中,梁的端点振动情况如图20所示。由图20可知,对日定向姿态的梁端点振幅约为0.63 m,而准对日定向姿态的梁端点振幅约为0.017 m。
通过以上研究发现,在梁的结构振动影响下,准对日定向姿态出现了较小的姿态误差,从而需要控制力矩来维持,但姿态误差和控制力矩都很小。同时,准对日定向姿态下梁的振动比对日定向姿态下梁的振动幅值减小约40倍。

图18 梁的姿态控制误差Fig.18 Attitude control errors of the beam

图19 梁的姿态控制力矩Fig.19 Attitude control moment of the beam

图20 梁端点的振动Fig.20 Vibration of the tip point of the beam
5 结 论
本文研究了针对大型太阳能电池阵列俯仰姿态的准对日定向姿态方案,并通过弦割法给出了准对日定向姿态的初值。此方案与以往的准惯性定向姿态方案不同的是,此方案能适应太阳方向的长期、缓慢变化。准对日定向姿态在一天内的平均发电效率能达到对日定向姿态的97.3%。对于Abacus空间太阳能电站的离子推进姿态控制方式而言,准对日定向姿态每年能节省约36791 kg控制燃料。为了保证准对日定向姿态的稳定性,设计了比例-微分控制器。通过数值仿真发现,当控制器的带宽大于ωc=5×10-5时,即可保证静止轨道上的太阳能电池阵列几乎在所有初始条件下均收敛到准对日定向姿态。最后,本文还讨论了轨道运动、姿态运动和结构振动对准对日定向姿态的影响。研究发现,在离心率不为零的情况下,存在准惯性定向姿态但不存在准对日定向姿态,而在离心率为零时轨道高度对准惯性定向姿态没有影响。在太阳能电池阵列姿态受控的情况下,偏航运动和滚转运动对俯仰运动的准对日定向姿态的影响都是高阶小量,从而可以忽略以简化分析过程。结构的振动会引起准对日定向姿态出现微小的姿态误差,从而需要姿态控制器维持;准对日定向姿态所需要的姿态控制带宽、姿态误差、姿态控制力矩和结构振动幅值跟对日定向姿态相比都小1~2个数量级。
