陪位中线与陪位重心

汪学思

(安徽省安庆市第二中学东区 246003)

三角形的中线是大家熟知的，但陪位中线却鲜为人知.如图1，AD是△ABC的中线，点D′在BC边上，若满足∠BAD=∠CAD′，则称AD′为△ABC的一条陪位中线(也称为共轭中线).我们知道三角形的三条中线交于一点，该点是三角形的重心.三角形的三条陪位中线也相交于一点，这个点就是三角形的陪位重心(也称为三角形的共轭重心).其证明如下：

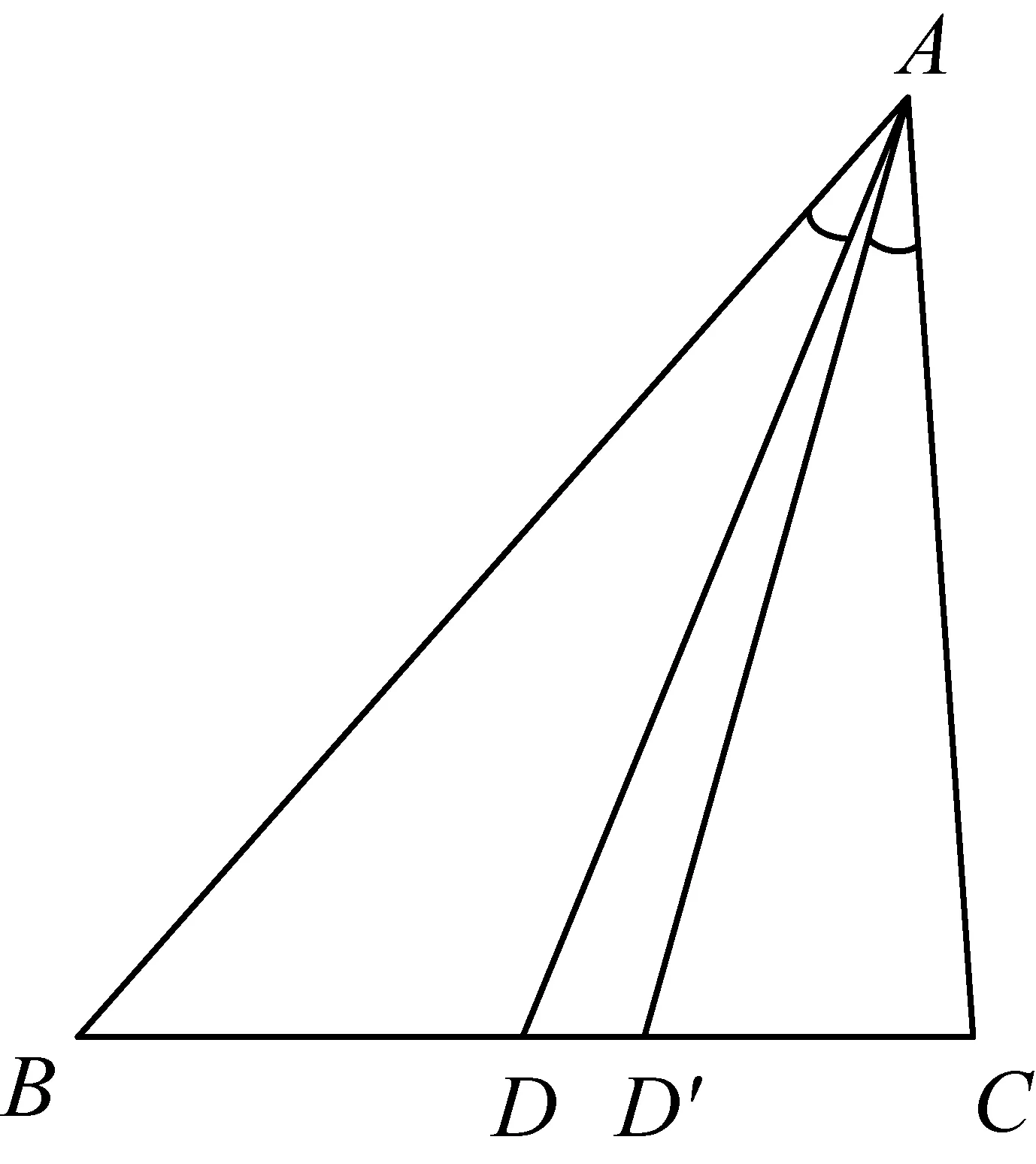
图1

图2

如图2，在△ABC中，AD′是中线，AD、BE、CF分别是其三条陪位中线.

则S△ABD′=S△ACD′

⟺AB·sin∠BAD′=AC·sin∠CAD′

因为AD为陪位中线⟺∠BAD=∠CAD′

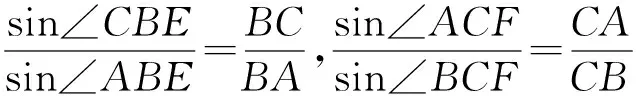
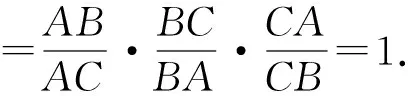
所以由Ceva定理知AD、BE、CF三线共点.

若设其交点为K，则点K为△ABC的陪位重心.

因为AD为陪位中线

所以由以上过程我们可得如下三角形陪位中线性质.

性质1(1)AD是△ABC的陪位中线

下面来讨论三角形陪位中线与陪位重心的另一些有趣的性质.

性质2如图3，AD为△ABC的陪位中线，E、F两点分别在AC、AB上，满足DE∥BA、DF∥CA，则有F、B、C、E四点共圆.

证明因为AD是△ABC的陪位中线，

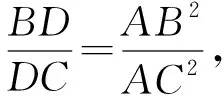
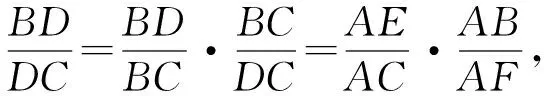
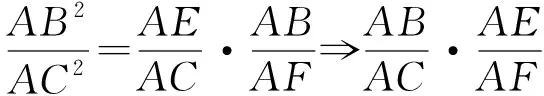
⟹AB·AF=AC·AE，

从而得到F、B、C、E四点共圆.

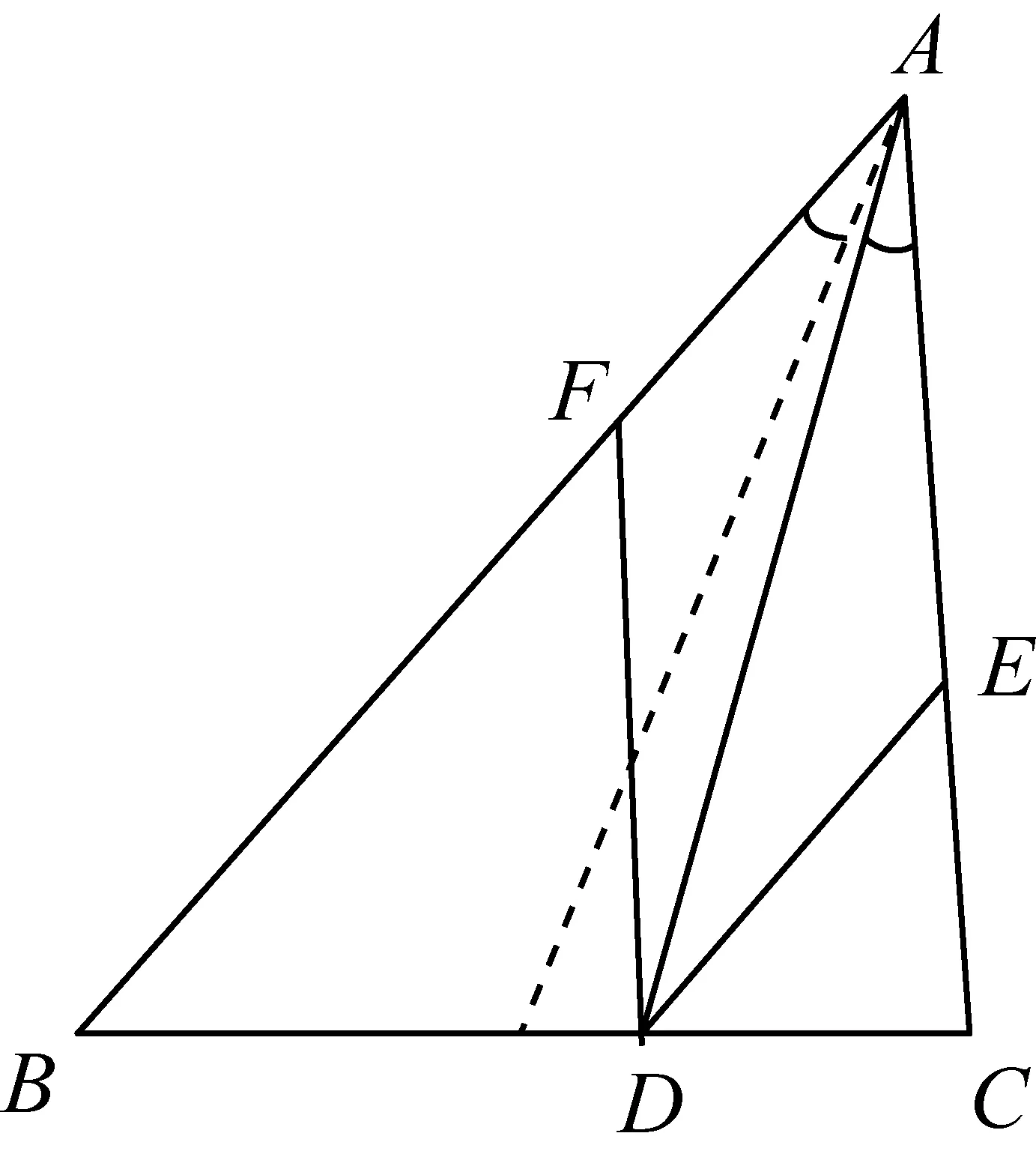
图3

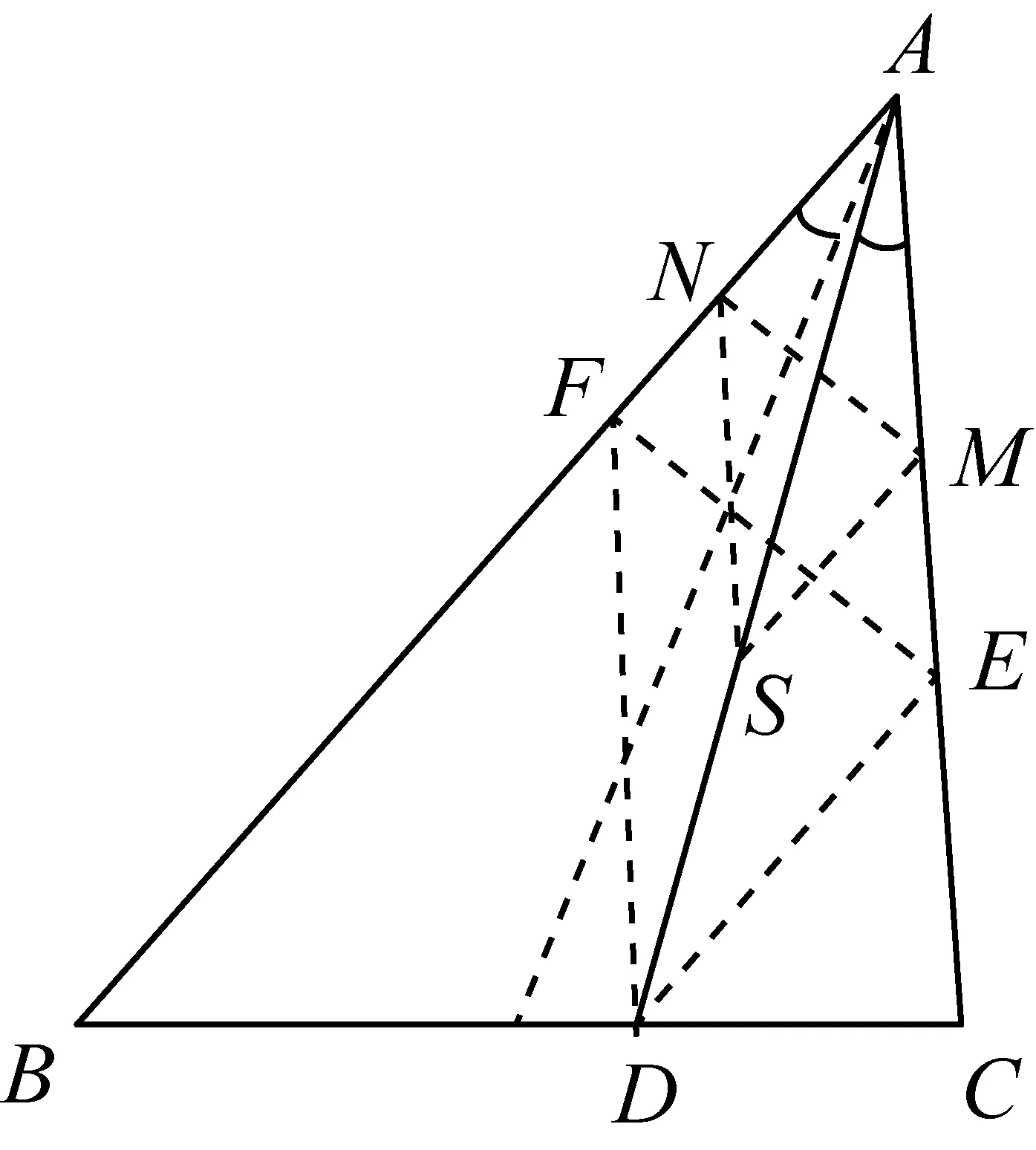
图4

性质3如图4，AD为△ABC的陪位中线，M、N两点分别在AC、AB上，若B、C、M、N四点共圆，则AD平分MN.[1]

证明作DE∥BA，DF∥CA交AC、AB于E、F点，连结EF.由性质2知B、C、E、F四点共圆⟹∠AEF=∠ABC.

作MS∥DE交AD于S，连结NS，

由B、C、M、N四点共圆，有∠AMN=∠ABC；

因为∠AMN=∠AEF，所以MN∥EF.

此时四边形AMSN为平行四边形，

所以AS平分MN，即AD平分MN.

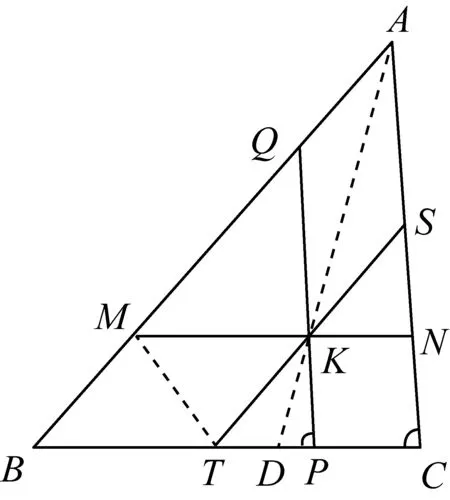
图5

性质4如图5，点K是△ABC的陪位重心，过K点作MN∥BC、PQ∥CA、ST∥AB，M、N、P、Q、S、T都在△ABC的边上，则有上述六点共圆．

证明连结AK并延长交BC于D点.

因为点K是△ABC的陪位重心，

所以AD必是△ABC的陪位中线.

所以AK是△AMN的陪位中线.

由于KS∥AM，KQ∥AN，利用性质2，

可得M、N、S、Q四点共圆 ①

同理P、Q、M、T四点共圆 ②

S、T、P、N四点共圆 ③

连结MT，因为

∠TMN=180°-∠AMN-∠BMT

=180°-∠ABC-∠BPQ(由②得)

=180°-∠STC-∠ACB=∠TSN，

所以M、T、N、S四点共圆 ④

比较③、④可得M、T、P、N、S五点共圆；

再比较②，则得到M、T、P、N、S、Q六点共圆.

性质4是由三角形陪位重心而得到的一组六点共圆(此圆被称为第一勒穆瓦纳(Lemoine)圆[2]).

下面的性质5提示的又一组六点共圆也是由三角形陪位重心得到的.

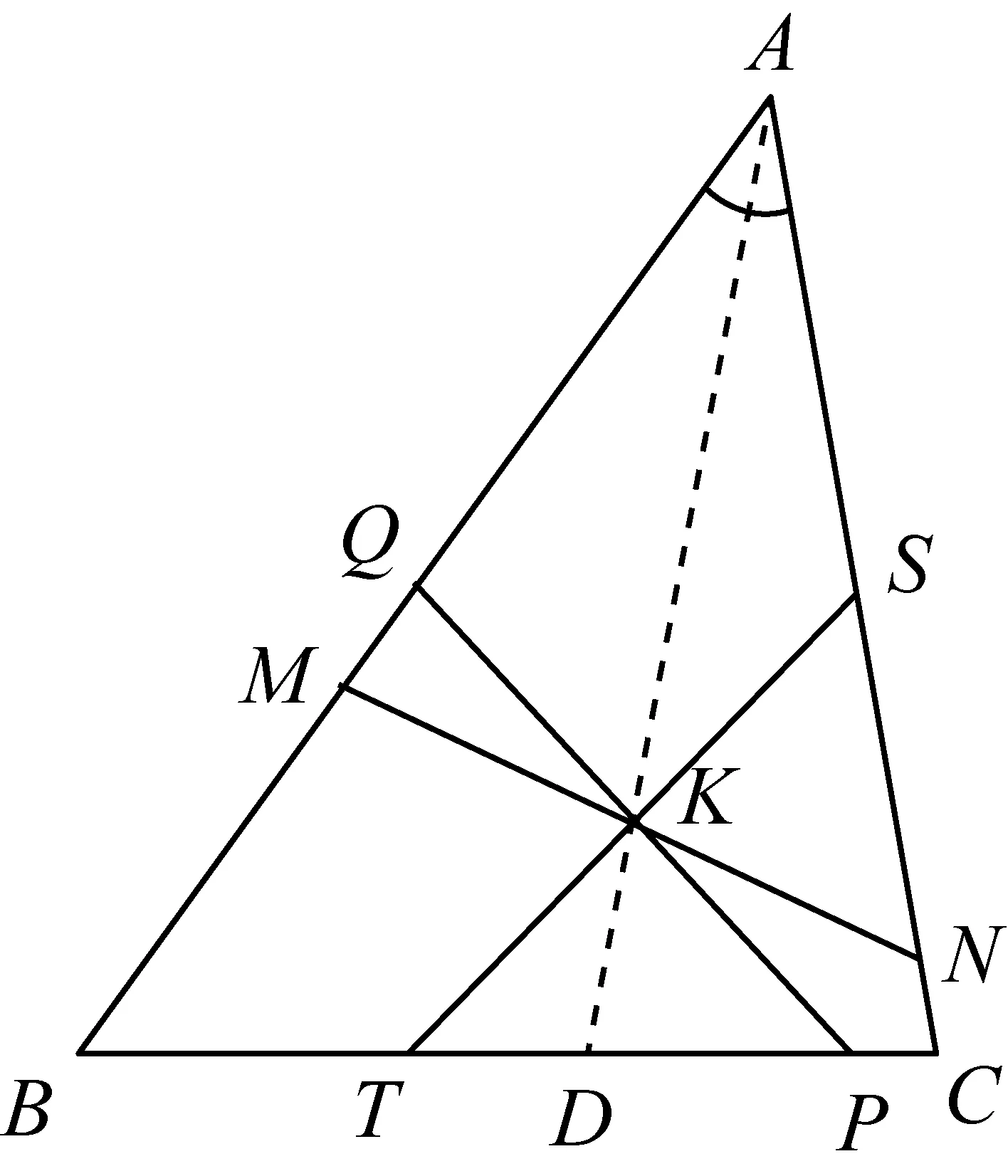
图6

性质5如图6，过△ABC的陪位重心K作三直线交各边于M、N、P、Q、T、S，若B、C、N、M四点共圆，C、A、Q、P四点共圆，A、B、T、S四点共圆，则有M、N、P、Q、T、S六点共圆.

证明由已知的三组四点共圆，易得

∠KTP=∠BAC=∠KPT⟹KT=KP；

同理KN=KS，KQ=KM①

连结AK并延长交BC于D，

则AD为△ABC的陪位中线.

由B、C、N、M四点共圆，

利用性质3可得KM=KN.

同理KP=KQ，KT=KS②

比较①、②得

KM=KT=KP=KN=KS=KQ.

所以M、N、P、Q、T、S六点共圆，并且这个六点圆的圆心就是△ABC的陪位重心K(此圆被称为第二勒穆瓦纳(Lemoine)圆[2]).

观察图6，记△ABC的三内角分别为∠A、∠B、∠C，

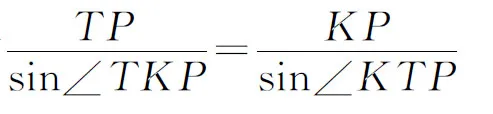
同理NS=2KScos∠B，QM=2KMcos∠C

⟹TP：NS：QM=cos∠A:cos∠B:cos∠C.

故可得如下性质.

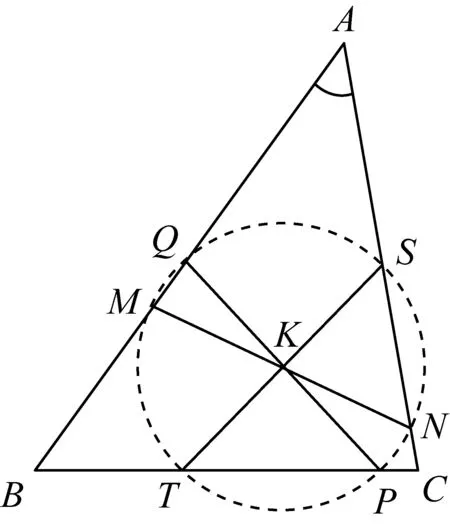
图7

性质6如图7，在性质5的前提下，M、N、P、Q、T、S六点圆在△ABC三边上截得的三条弦长的比是

TP∶NS∶QM= cos∠A∶cos∠B∶cos∠C.

现在我们回顾性质4，参见图5，由陪位重心K得到的六点共圆在△ABC各边上截得的弦长TP：NS：QM又有什么结论呢？请看下面的性质.

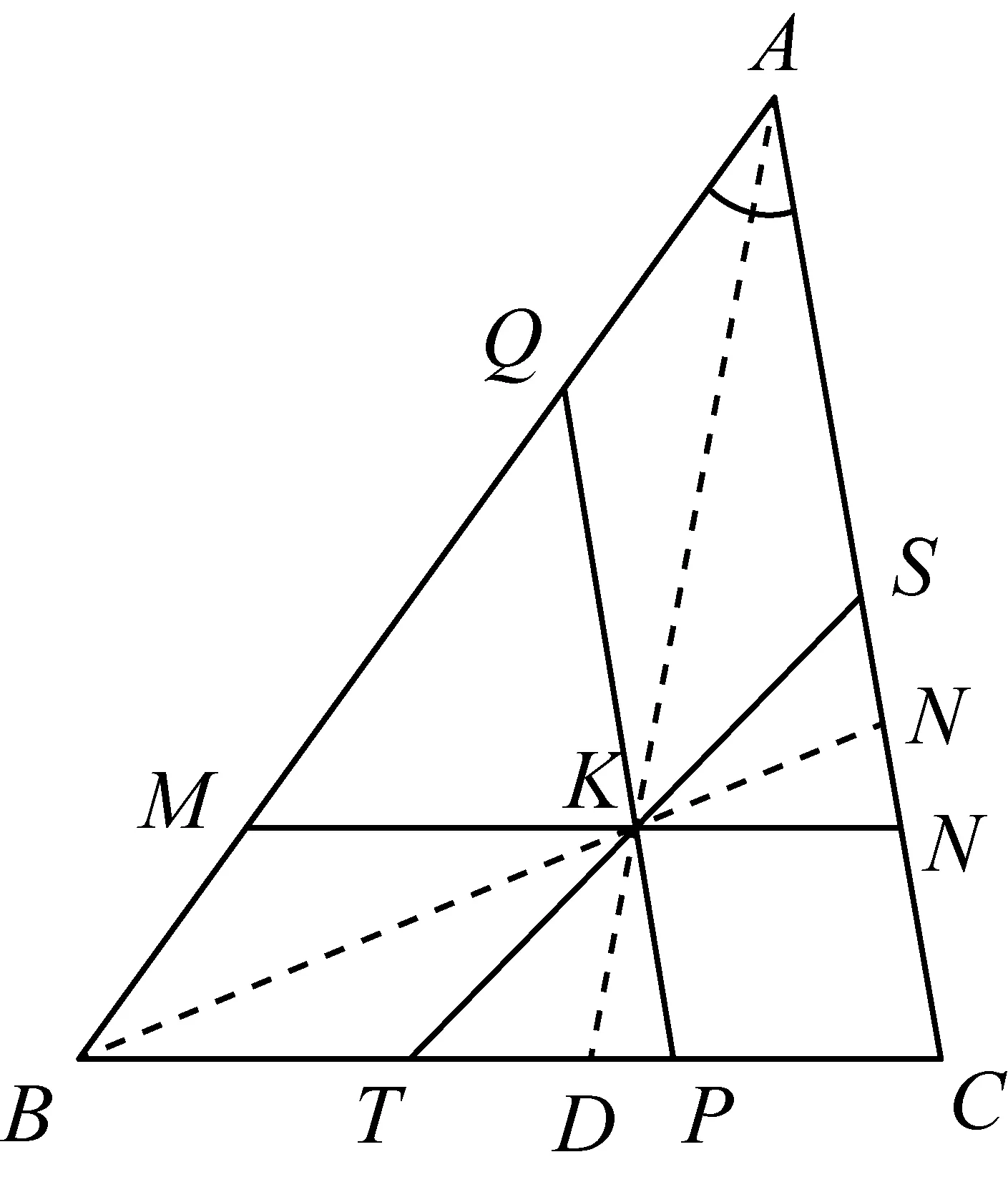
图8

性质7如图8，过△ABC的陪位重心K作MN∥BC、PQ∥CA、ST∥AB.点M、N、P、Q、T、S在三边上，记BC=a、CA=b、AB=c，则有TP∶NS∶QM=a3∶b3∶c3.

证明连结AK、BK并延长分别交BC、CA于D、E点.

因为点K是△ABC的陪位重心，

所以AD、BE都是陪位中线.

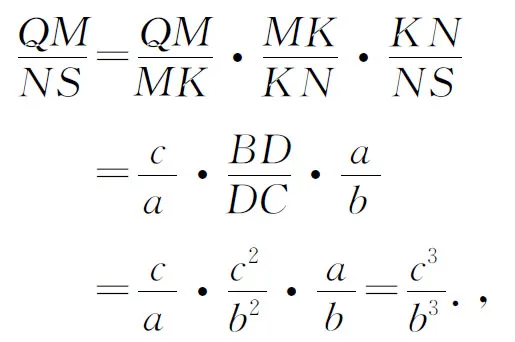
所以TP∶NS∶QM=a3∶b3∶c3.

图9

性质8如图9.在锐角△ABC中，点D在边BC内，△ABC的外接圆O上的过B、C的切线相交于E点，则AD为△ABC的陪位中线的充要条件为A、D、E三点共线.[3]

因为过三角形的一个顶点作对边的平行线，与该顶点的中线及三角形过该顶点的两条边组成调和线束，过此顶点的圆截这调和线束四条射线的交点组成的四边形为调和四边形.

当性质8的A、D、E三点共线时，利用相似三角形进行推导，并由性质1(2)，可得如下性质.

性质9圆内接四边形为调和四边形的充要条件是其一条对角线为另一条对角线分该四边形所成三角形的陪位中线.[3]

有了上述这些知识准备，现在来解决一些问题，就比较容易了.

例1在△ABC中，过点C作其外接圆⊙O1的切线交AB延长线于点D，再过A、C分别作△ACD的外接圆⊙O2的切线，两切线交于P点.

求证：直线DP平分线段BC.

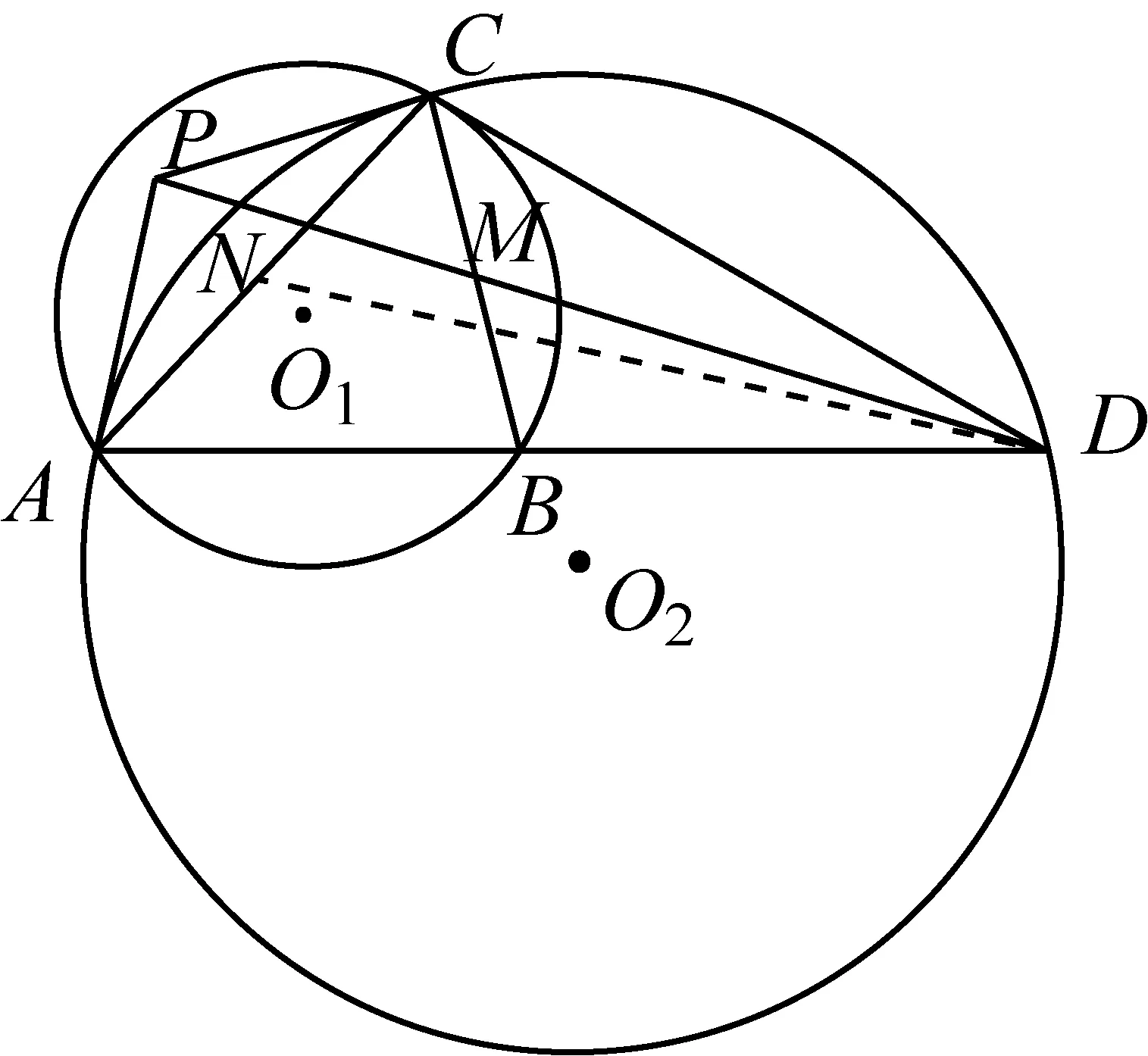
图10

证明如图10，设PD交BC于M点，AC中点为N，连DN.

因为PA、PC为⊙O2在A、C处的切线，

所以由性质8，DP为△ADC的陪位中线所在直线.

因为∠CAD=∠BCD，∠ADC=∠CDB，

所以△ACD∽△CBD.

因为∠ADN=∠CDM，

所以AN与CM为对应线段，

又AN=NC，

所以得CM=MB，即直线DP平分线段BC.

例2设△ABC是非等腰锐角三角形，其高线AD、BE相交于H点. △ABH的重心为G点，若CG平分线段DE，试求∠ACB的度数.

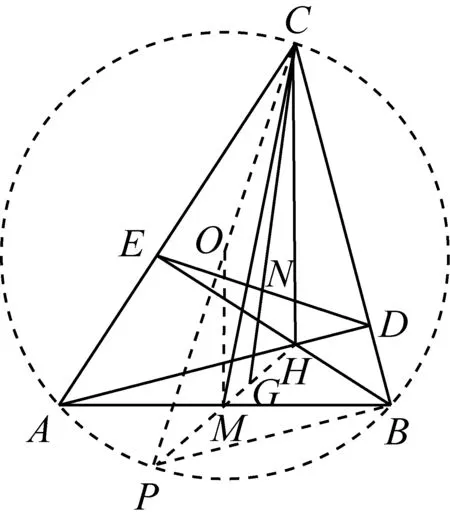
图11

解如图11，设△ABC的外接圆心为O点，连CO延交⊙O于P点，连PA、PB、PH.

由BH⊥AC，PA⊥AC，得PA∥BH.

同理可得PB∥AH.

所以四边形AHBP为平行四边形；

令AB中点为点M.

因为G点为△ABH的重心，

故H、G、M、P四点共线，且有PG∶GH=2.

因为CG平分线段DE，设CG∩DE=N，

则DN=EN.

由A、B、D、E四点共圆，可得△CDE∽△CAB.

又由N、M点为DE、AB中点，

可得∠NCD=∠MCA.

又因为∠BCH=∠ACP，

所以∠HCG=∠PCM.

所以由定义，CG是△CHP的陪位中线.

连OM，可得CH=2·OM=CP·cos∠ACB，

所以所求ACB=45.

例3在△ABC中，K点为其陪位重心，BE垂直于AC，E为垂足，若∠AKE= 180°-2∠BAC，求证：∠CKE= 180°-2∠ACB.

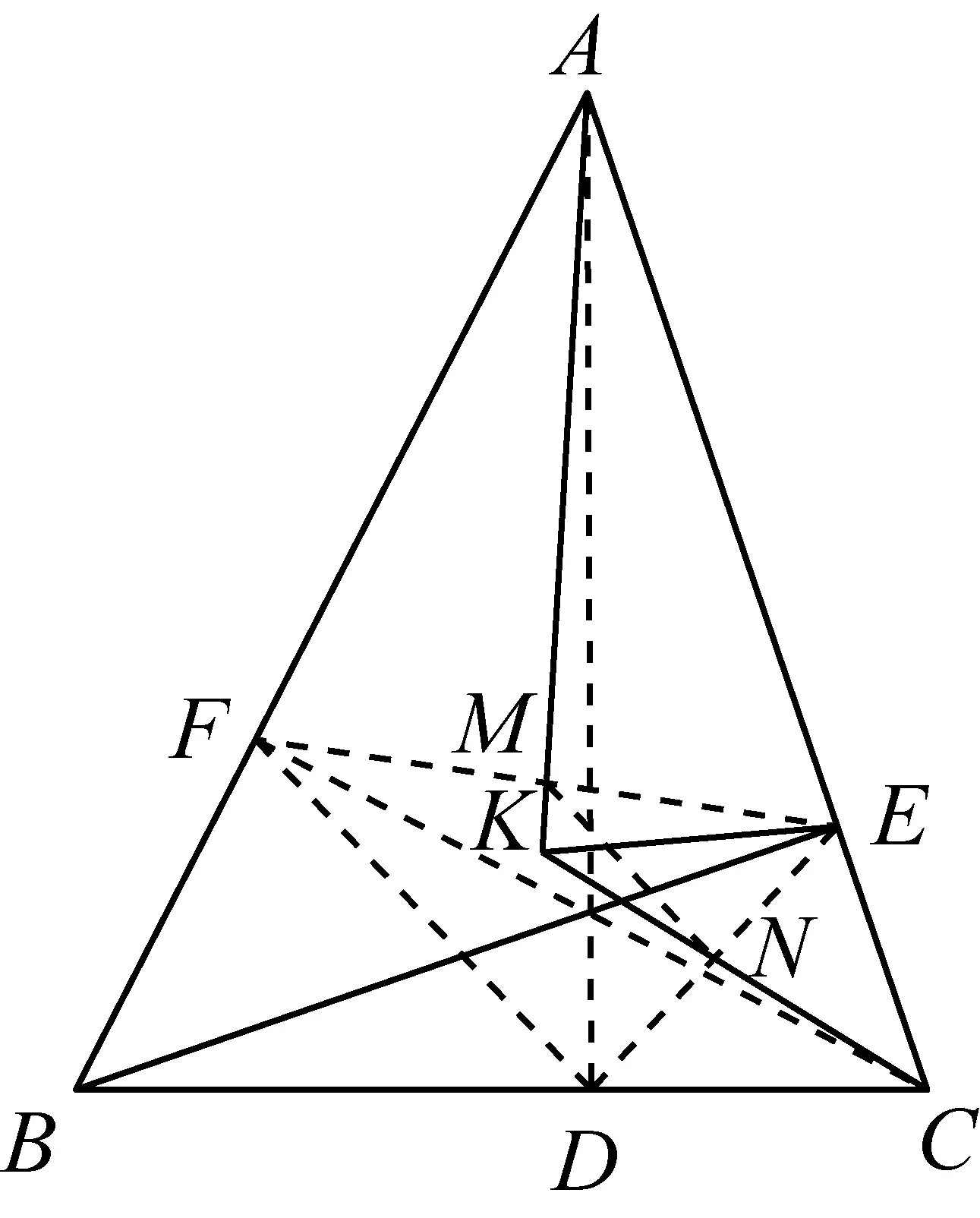
图12

证明如图12，作AD⊥BC交BC于D点，CF⊥AB交AB于F点.设EF、ED的中点分别为M、N.

因为∠BFC=∠BEC=90°，

所以B、C、E、F四点共圆.

故有△AEF∽△ABC.

因为K点为△ABC的陪位重心，

所以AK是△ABC的陪位中线，

所以由性质3，AK是△AEF的中线.

即A、M、K三点共线.

同理可得C、N、K三点共线.

所以MN∥FD，∠MNE=∠FDE.

因为已知∠AKE=180° -2∠BAC，

再由A、B、D、E四点共圆，A、C、D、F四点共圆.

所以∠FDE=180°-(∠BDF+∠CDE)

=180°-2∠BAC=∠AKE=∠MKE.

故∠MNE=∠MKE，M、K、N、E四点共圆；

所以∠CKE=∠NKE=∠NME=∠DFE

=180°-2∠ACB.

例4(2005国家集训队选拨考试题(二)第五题)设锐角△ABC的外接圆为ω.过点B、C作ω的两条切线相交于点P，连结AP交BC于点D，点E、F分别在边AC、AB上，使得DE∥BA、DF∥CA.

(1)求证：F，B，C，E四点共圆；

(2)若记过F、B、C、E的圆的圆心为A1，类似地定义B1、C1，则直线AA1、BB1、CC1共点.

证明(1)由题意，如图13.根据性质8可得AD是陪位中线.

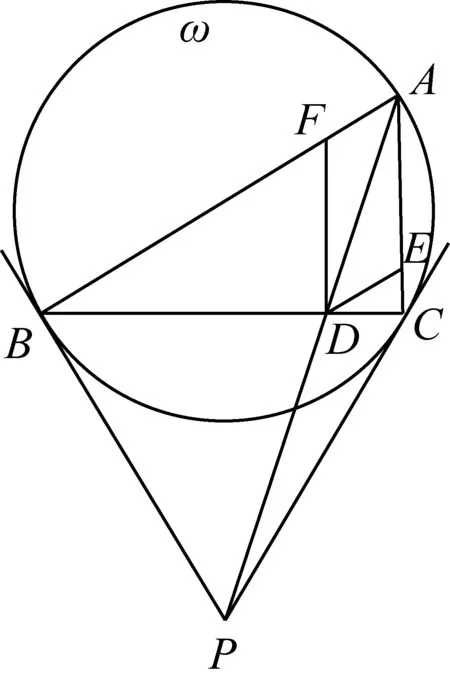
图13

再由性质2得F、B、C、E四点共圆.

(2)设△ABC的陪位重心为K，则K在AD上.

观察图5，令由陪位重心K得到的六点圆的圆心为O(显然O点具有唯一性)，由于四边形MNSQ的顶点共圆，它的圆心就是O点.易证图5中的四边形MNSQ与图13中的四边形BCEF是两个位似形，其位似中心是A点，由位似形性质，可得A、O、A1三点共线，即AA1通过O点；

同理BB1、CC1也通过O点，

所以AA1、BB1、CC1三线共点.

图14

例5在△ABC中，已知顶点A、重心G和其经过A点的陪位中线所在直线与△ABC外接圆的交点为S，然后擦去点B、C及其外接圆，如图14.请从保留的三个已知点A、G、S出发，作图画出原△ABC.

解本题在给出定点A、G、S的情形下，按照以下作法，可作出原△ABC.

作法步骤：

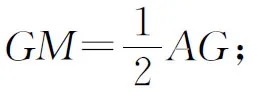
2.以M为圆心，MS为半径作圆c1；

3.设AM的延长线交圆c1于点T；

4.作△AST的外接圆为c2；

5.过M作TS的平行线交圆c2于点B、C；

6.连结A、B、C，则△ABC即为所求，如图15.

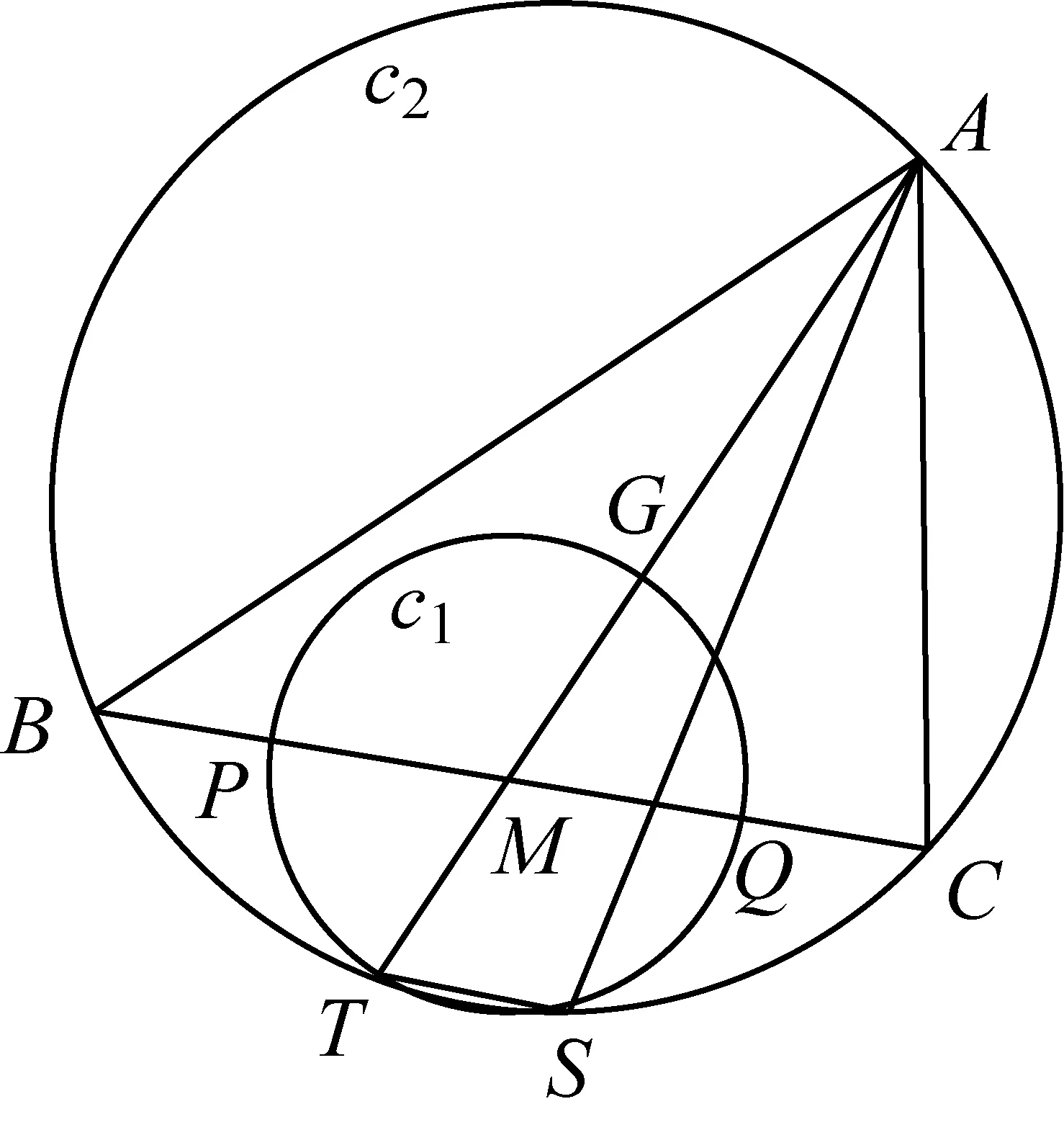
图15

证明因为A、G、S都是定点，

由作法知BC∥TS，

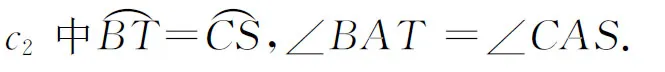
若设圆c1交BC于P、Q点

则△BPT≌△CQS.

所以BP=CQ，故BM=CM，M为BC中点.

再由∠BAM=∠CAS知，

△ABC中过A点的陪位中线在直线AS上.

综上，上述作法作出了原△ABC.

例6△ABC的外接圆为⊙O，过B、C点分别作⊙O的切线相交于D点，边AC、AB的中点分别为E、F点，DC交BE于P点，DB交CF于Q点.

求证：∠BAQ=∠CAP.

证明由题意可知，设BE∩CF=G，

则G为△ABC的重心，如图16.

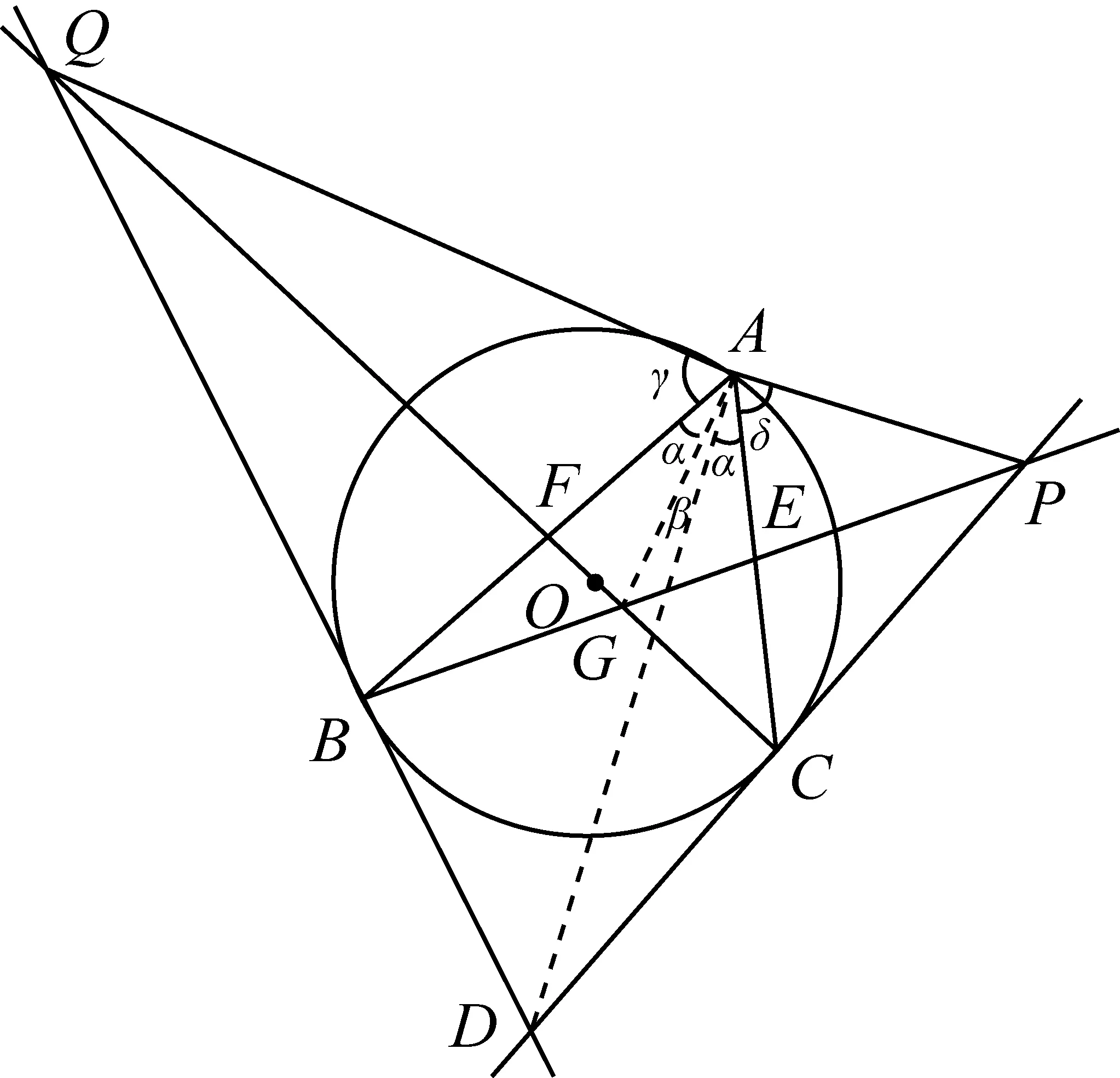
图16

因为DB、DC是△ABC外接圆⊙O的切线，

所以由性质8，直线AD为△ABC的陪伴中线所在直线，∠BAG=∠CAD.

设∠BAG=∠CAD=α，∠DAG=β,

∠BAQ=γ,∠CAP=δ.

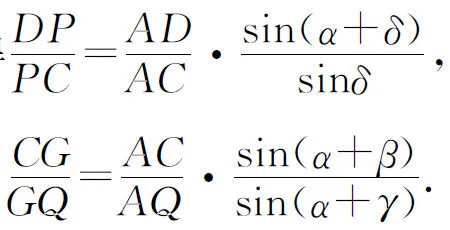
因为△CDQ被直线PGB所截，

所以由Menelaus定理有

即∠BAQ=∠CAP.

例7在△ABC中，AB>AC，过点A作△ABC的外接圆⊙O的切线，与BC的延长线交于点D，E为AD的中点 ，BE与⊙O交于点F．

求证：直线AF是△ACD的陪位中线所在直线.

证法一如图17，因为AE为⊙O切线，E为AD中点，连接DF，

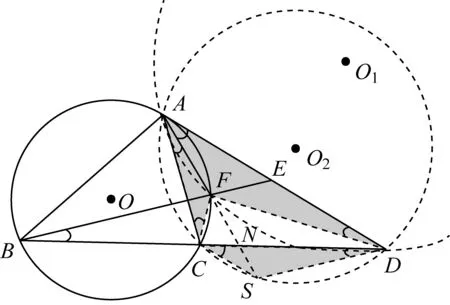
图17

所以ED2=EA2=EF·EB⟹△DEF∽△BED⟹∠FDA=∠DBE=∠FAC=∠SDC.

过点A、F、D作圆⊙O1，过点A、C、D作圆⊙O2，延长AF交CD于点N、交⊙O2于点S，

连接FC、CS、DS，

又因为∠ACF=∠DAF=∠DCS，

所以△ACF∽△DAF∽△DCS

由性质1(2)可得，直线AF是△ACD的陪位中线所在直线．

证法二如图18，连接CF、DF.

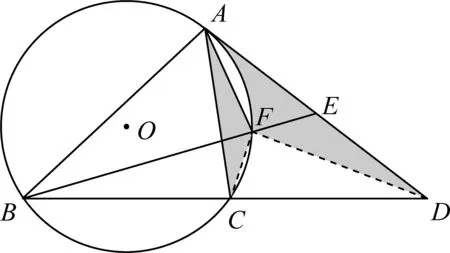
图18

因为AE为⊙O切线，E为AD中点，

所以ED2=EA2=EF·EB

⟹△DEF∽△BED

⟹∠FDA=∠DBE=∠FAC.

又∠DAF=∠ACF，

所以△ACF∽△DAF.

由性质1(1)可得，直线AF是△ACD的陪位中线所在直线．

此两种证法都可谓典型.证法一的证明过程中，通过作辅助线，从中展示了其内在的各点线间的关系，虽繁杂却有序；证法二辅助线很少，体现出一种精巧的细致美，给人以一种“简约而不简单 丰富而不繁复”的感受.