教材分析：从理解走向探究

刘昊懿 徐章韬

(华中师范大学数学与统计学学院 430079)

平面几何的研究对象仍然是解析几何的研究对象.从教材分析中可以知道，直线、圆的方程是解析几何教材花笔墨介绍了的，那么我们不禁要问：平行四边形系列的图形有相应的方程吗？如果有，它们的方程应是什么样的？从平行四边形到正方形是强抽象的过程，是不断丰富概念内涵的过程；从正方形到平行四边形是弱抽象的过程，是不断扩张概念外延的过程.在这个概念外延扩张的过程中，存在着“正方形—菱形—平行四边形”“正方形—矩形—平行四边形”两条路线.因此在常见四边形方程探索的过程中，可以从图形上最简单的正方形着手，利用直角坐标系，来研究正方形上点的坐标所满足的方程；再将菱形或者矩形作为中转站，通过坐标系的变换来回归到已知四边形的方程，最终得到平行四边形的方程.

下面是在教材深度分析中，通过探究来理解教材的一个案例.这个案例的作用不只是为了填补教材中没有平行四边形系列图形方程的空白，而是为了阐明一种一以贯之的思考路径.

1 技术路线

1.1 正方形的方程

利用坐标系得到函数方程的过程中，根据图形的几何性质，有技巧地建立坐标系可以大大简化思维与计算.而由于正方形图形上的特殊性，在不同的直角坐标系中，都能够通过坐标系的变换，做到“以不变应万变”.

(1)设任意正方形的对角线长为2a时，以正方形的中心为原点，两条对角线所在的直线为坐标轴建立直角坐标系，如图1，则由直线的斜截式方程得到：在此种建系方法下，正方形上点的坐标所满足的方程为：

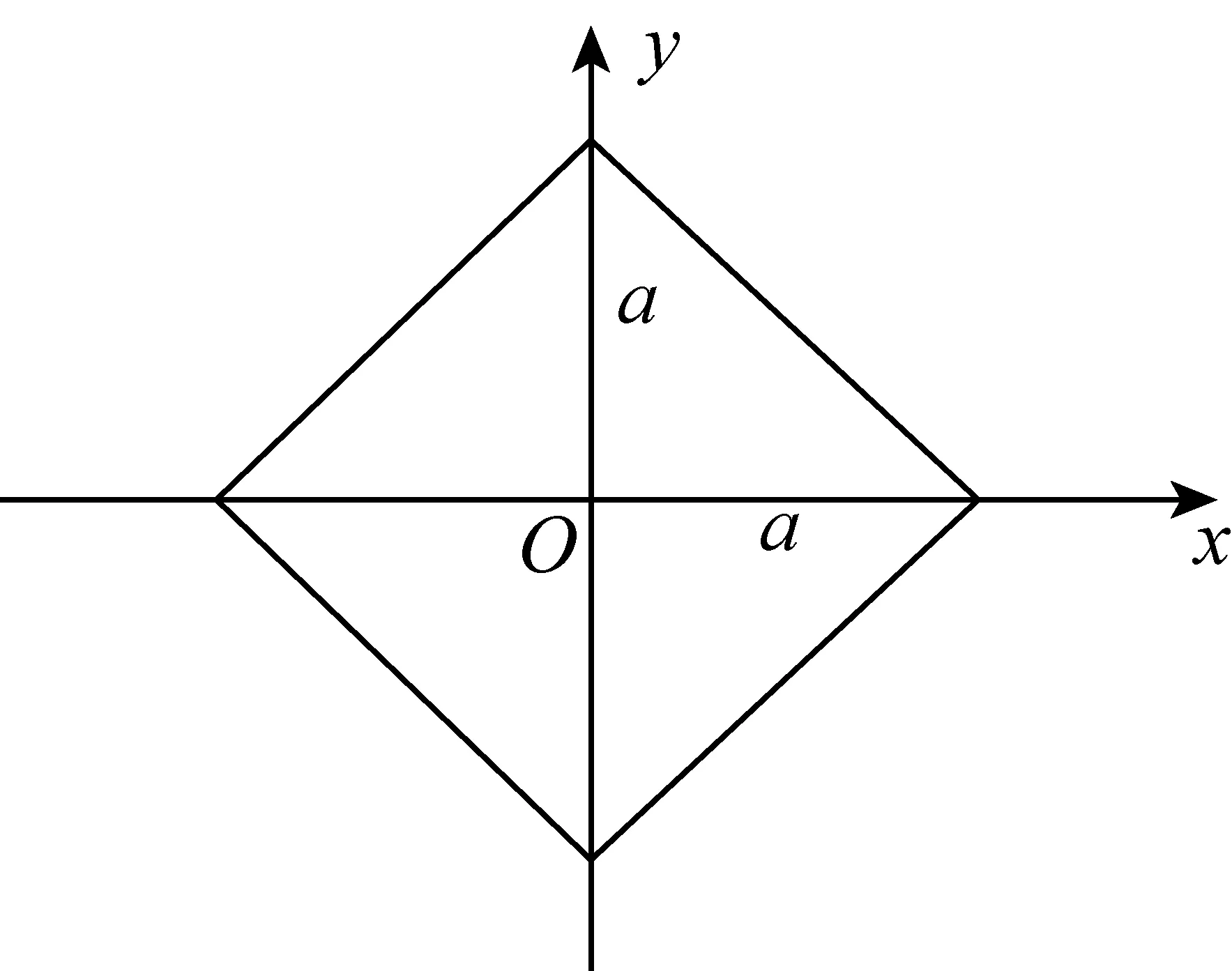
图1

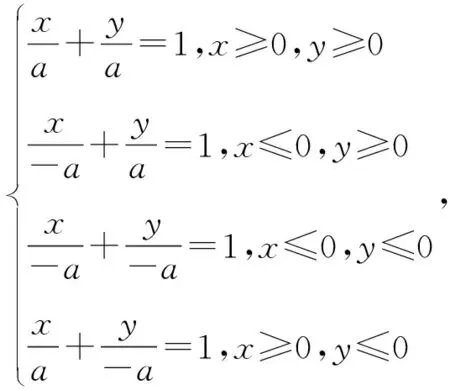
以上分段式方程可合并为：

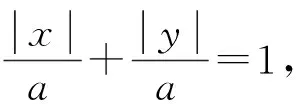
其中a为正方形对角线长的一半.

(2)设任意正方形的对角线长为2a时，以正方形的中心为原点，平行于正方形的两边建立直角坐标系.通过将直角坐标系进行：原点不变，坐标系逆时针旋转45°的变换，得到新的直角坐标系，则将新的建系情形化归到已探讨过的建系情形，如图2，则对原直角坐标系中(x,y)在新的直角坐标系中对应的(x′,y′)，由直角坐标系的坐标旋转公式，有：

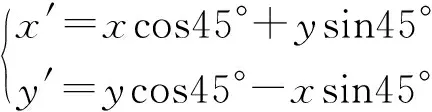
代入方程①得：在此种建系方法下，正方形上点的坐标所满足的方程为：

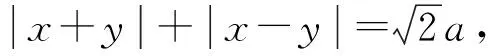
其中a为正方形对角线长的一半.

(3)由于正方形图形上的特殊性，无论以正方形的中心为原点，如何建立直角坐标系，都可以运用上述方法，将直角坐标系进行旋转变换，此时运用的直角坐标系的坐标旋转公式为：

其中θ为直角坐标系逆时针旋转的角度，由于运动的相对性，不旋转坐标系，旋转图形也是可以的.

1.2 从正方形到菱形的方程

正方形是有一个角为直角的菱形，因此通过拓展正方形的概念外延，可以得到菱形.将正方形看成菱形的特殊情形，菱形上点的坐标所满足的方程也就可以考虑通过已知的正方形来探索.

考虑到菱形和正方形对角线都相互垂直的共同性质，为了尽可能地简化思维和计算，在此用上面的第一种建系方法来建立直角坐标系.

设任意菱形的对角线边长分别为2a，2b，以菱形的中心为原点，两条对角线所在的直线为坐标轴建立直角坐标系，如图3，则由直线的截距式方程得：在此种建系方法下，菱形上点的坐标所满足的方程为：

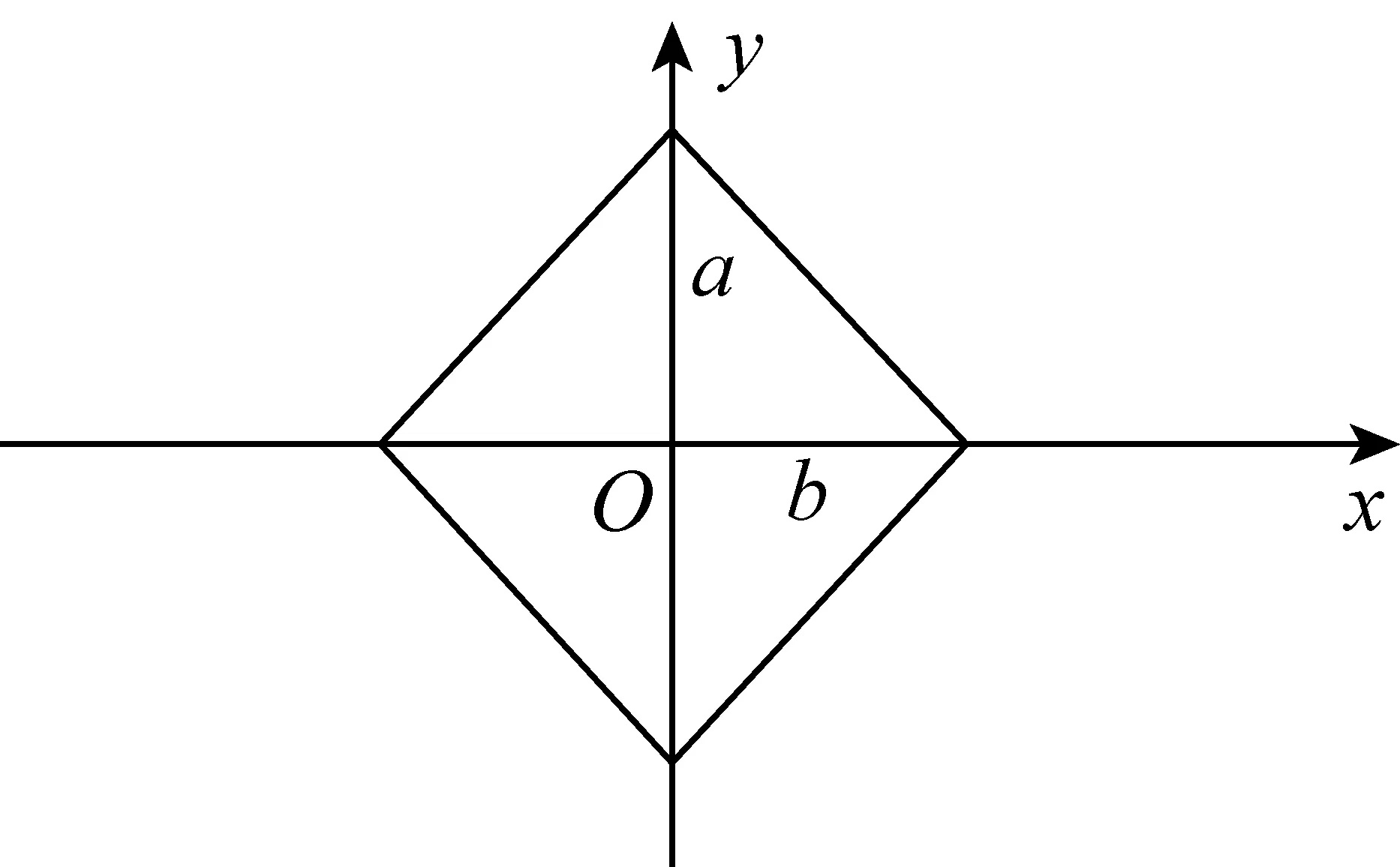
图3

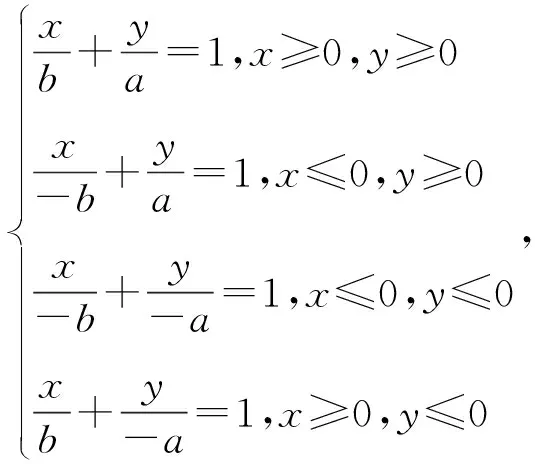
其中a，b分别为菱形两条对角线长的一半.

此外，将方程①与方程③进行类比与对比，也能够从代数的角度看到：正方形与菱形对角线都相互垂直；但正方形两条对角线长相等，菱形两条对角线长不相等的几何性质，让学生从数的层面重新认知了形的知识.

1.3 从正方形到矩形的方程

类似地，正方形是两条邻边相等的矩形，通过拓展正方形的概念外延，可以得到矩形.将正方形看成矩形的特殊情形，矩形上点的坐标所满足的方程也就可以考虑通过坐标系的变换，来将未知的矩形回归到已知的正方形来探索.

考虑到矩形和正方形四个角都是直角的共同性质，为了尽可能地简化思维和计算，在此用上面的第二种建系方法来建立直角坐标系.

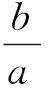
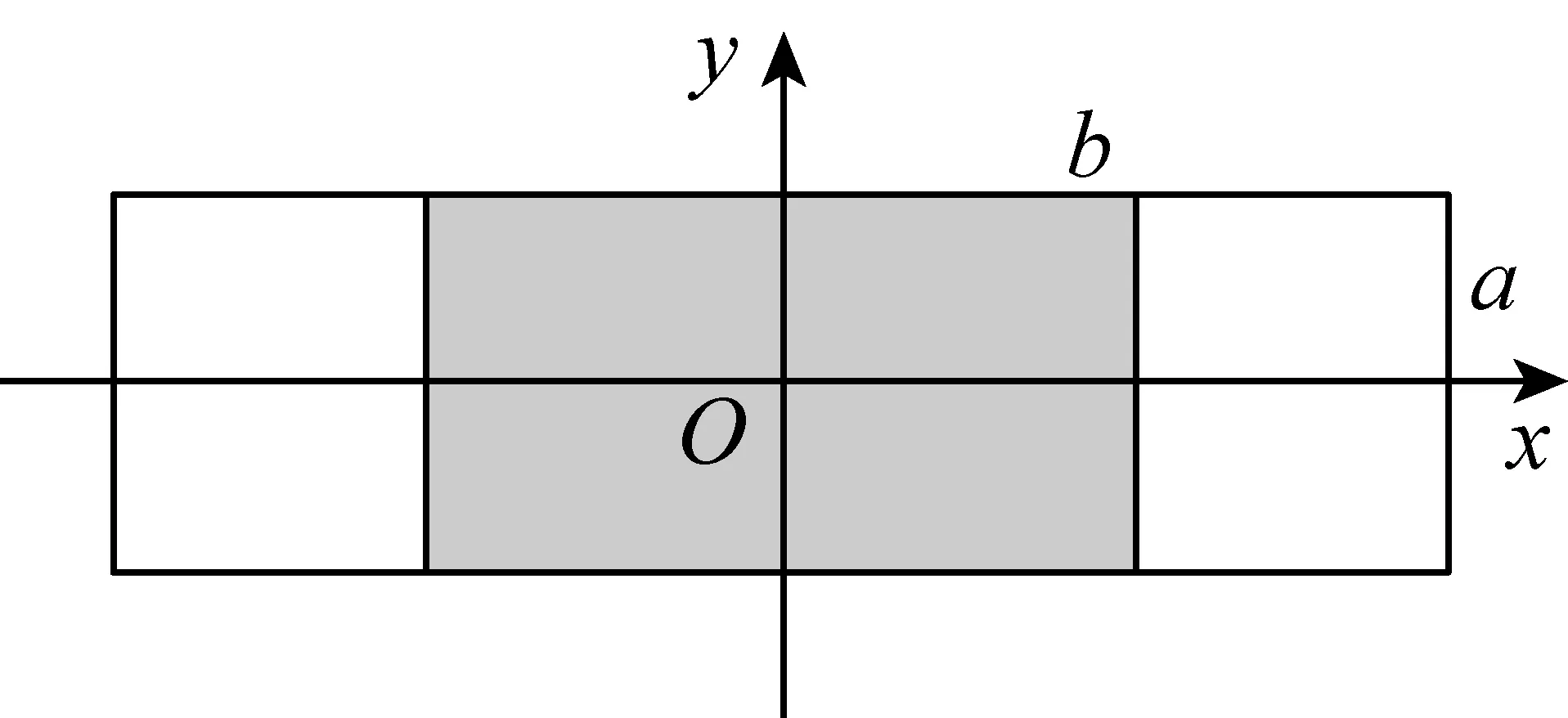
图4

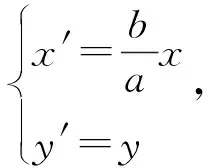
代入方程②得，在此种建系方法下，矩形上点的坐标所满足的方程为：

化简得|bx+ay|+|bx-ay|=2ab， ④

其中a，b分别为矩形两邻边长的一半且a>b.

同样地，将方程②与方程④进行类比与对比，能够从代数的角度看到：正方形与矩形四个角都为直角；但正方形两条邻边长相等，矩形两条邻边长不相等的几何性质，让学生从数的层面重新认知了形的知识.

1.4 从正方形到平行四边形的方程

菱形是两条邻边相等的平行四边形；矩形是一个角为直角的平行四边形.因此，通过拓展菱形或矩形的概念外延，都可以得到平行四边形.将菱形或矩形看成平行四边形的特殊情形，平行四边形上点的坐标所满足的方程也就可以考虑通过坐标系的变换，来将未知的平行四边形回归到已知的菱形或矩形来探索.

(1)正方形—菱形—平行四边形

考虑到菱形和平行四边形对角线都相互平分的共同性质，为了尽可能地简化思维和计算，在此用第一种建系方法来建立直角坐标系.

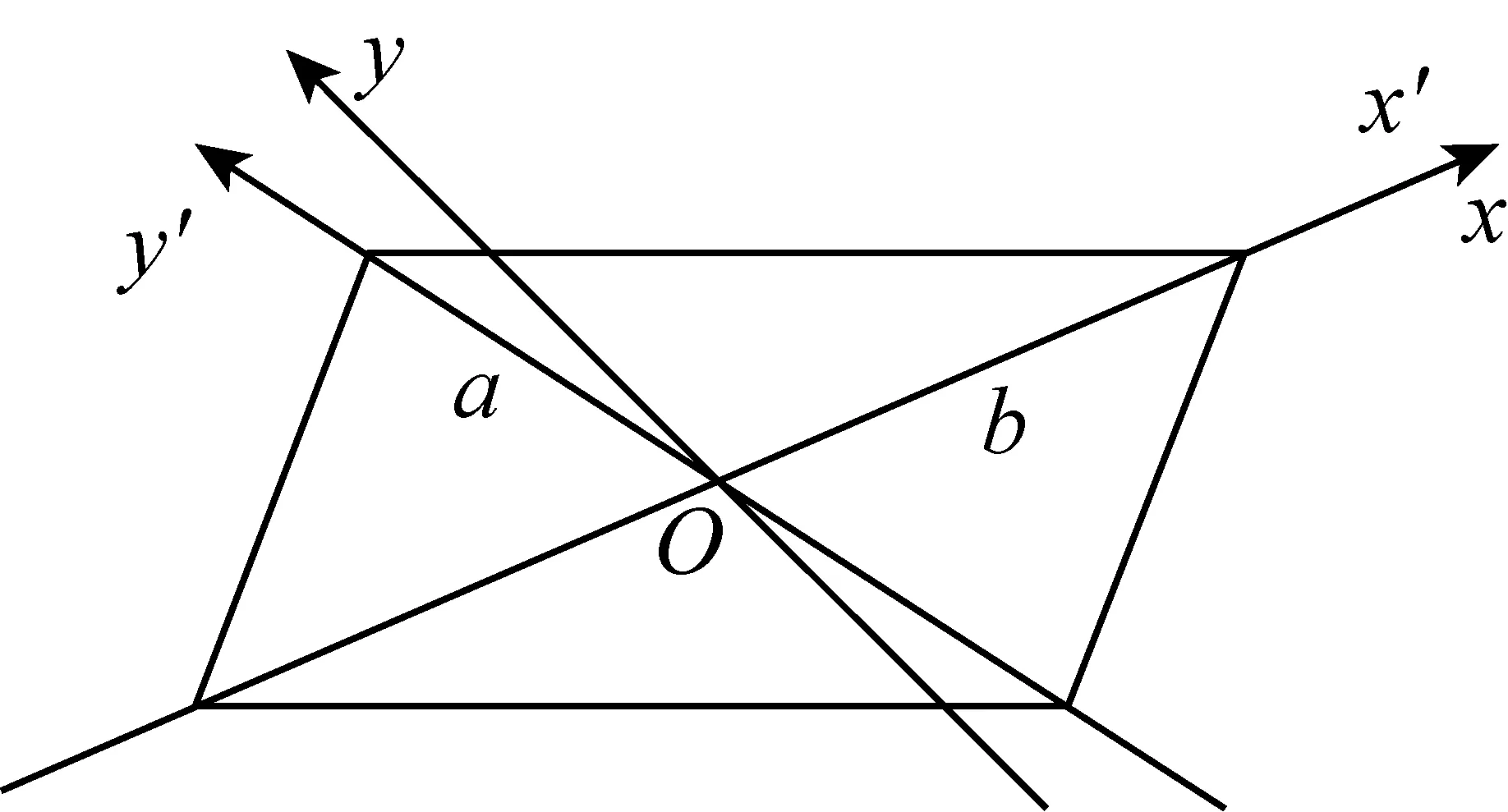
图5

代入方程③得到，在直角坐标系中，平行四边形上点的坐标所满足的方程为：

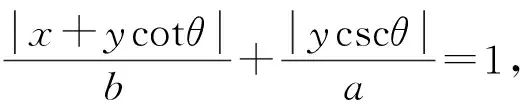
此外，将方程③与方程⑤进行类比与对比，也能够从代数的角度看到：菱形与平行四边形对角线都相互平分；但菱形两条对角线长相互垂直，平行四边形两条对角线长不相互垂直的几何性质，让学生从数的层面重新认知了形的知识.

(2)正方形—矩形—平行四边形

考虑到矩形和平行四边形对角线都相互平分的共同性质，为了尽可能地简化思维和计算，在此用第二种建系方法来建立直角坐标系.

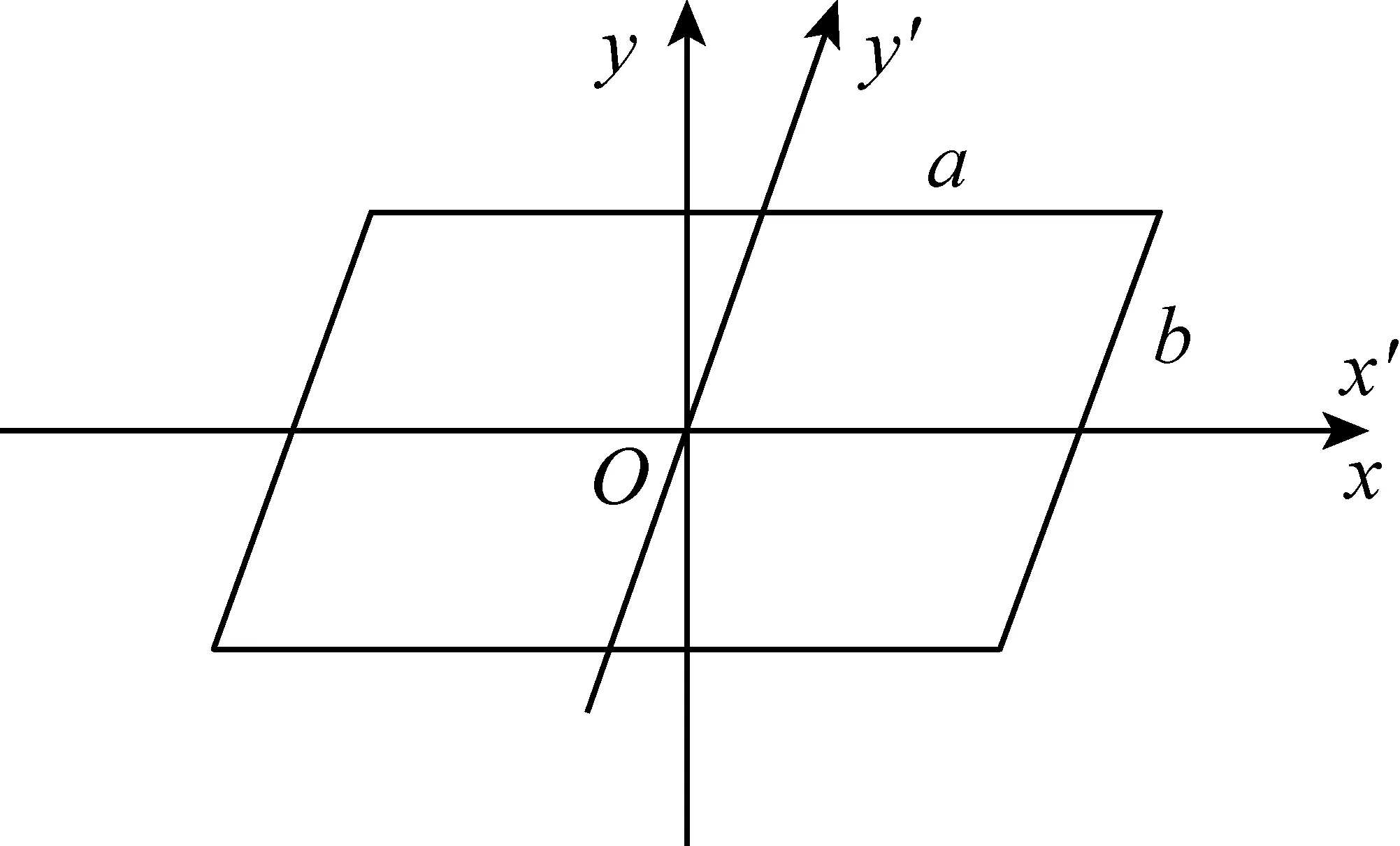
图6

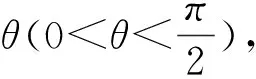
代入方程④得到，在直角坐标系中，平行四边形上点的坐标所满足的方程为：

|b(x-ycotθ)+aycscθ|+

|b(x-ycotθ)-aycscθ|=2ab， ⑥

同样地，将方程④与方程⑥进行类比与对比，也能够从代数的角度看到：矩形与平行四边形邻边都相互平行；但矩形两条邻边相互垂直，平行四边形两条邻边不相互垂直的几何性质，让学生从数的层面重新认知了形的知识.

2 分析与讨论

在上述过程中能够看到，采取的主体思路是：把握常见四边形的几何性质，巧妙地建立坐标系；根据“正方形—菱形—平行四边形”“正方形—矩形—平行四边形”两条路线，利用坐标系的变化，将研究正方形的方程中两个基本的建系方法延伸到其他常见四边形方程的探索中.

在这个过程中，既体现的是从特殊到一般的思想方法与探索过程，又在变换的过程中，带领学生从数与形的角度，深刻把握常见四边形概念之间条件的转化；并重新认识常见四边形之间几何性质的相同点与不同点，从不同层面为课本的主要内容做了补充；同时也建构了几何与代数之间沟通的桥梁，增添了课程的趣味性与深度.

对教材进行深度分析是教师的基本功之一.有两条基本路径.其中一条是对已有的文本进行多角度的理解，或者是从高观点解读、或者是从多角度解读、或者是从横向关联的角度进行解读.其目的在于“理解数学”，把已有文本后面的数学的精神、思想、方法揭示出来，让师范生获得不一样的体会.第二种路径是就通过探究来理解教材.就是进攻是最好的防御一样，做数学探究也是一种理解教材的好方式.数学教学应是数学研究的艺术性再现.在大学课堂教学中更应如此.本课例是在大学课堂教学中，通过教“基本套路”——从特殊到一般，一以贯之地思考问题而产生的一个思考结果.通过研究，不断填补了教材中从直线方程到圆的方程之间的平行四边形方程的断裂，更为重要的是培养了师范生，导引了他们的思考.