双沟水电站面板堆石坝变形反演分析

梁希林，刘 枫

（1.太平湾发电厂，辽宁 丹东 118000；2.中水东北勘测设计研究有限责任公司，吉林 长春 130061；3.水利部寒区工程技术研究中心，吉林 长春 130061）

1 研究背景

近年来，混凝土面板堆石坝应用越来越广泛，在工程实践过程中虽然加强了对堆石体的基本力学特性研究，但目前设计主要停留在工程类比和按经验设计阶段。仅仅依据设计阶段进行的大坝变形等的预测进行大坝结构安全性评价，存在较大的局限性，难以满足实际工程需要。从株树桥、成屏和天生桥等工程所暴露的问题来看［1-5］，在设计阶段进行大坝变形预测的同时，根据原型监测信息，结合大坝实际填筑料源与填筑标准的优化，加强施工期和运行期的反馈分析，对准确预测大坝的工作性态，指导大坝的施工及运行管理，确保大坝安全，具有重要的现实意义［6］。1985 年，吴中如等［7］用有限元法计算值与实际观测值进行最小二乘拟合，求得水压分量、温度分量和时效分量的调整参数，建立位移的确定性模型，并以佛子岭连拱坝坝顶水平位移进行了验证。1993 年由陈永奇教授在第七届国际测量师联合会（FIG）变形测量研讨会上介绍了灰色理论在变形监测分析中的应用，使得灰色理论在变形监测预测中得到了重视和推广［8］。沈珠江等［9-10］对堆石料的动力变形特性及堆石坝流变变形进行了研究，研究成果应用较为广泛［11-13］。近几年，邓肯E-B模型在一些工程上得到应用［14-15］，取得了较好的效果。根据混凝土面板堆石坝的组成与特点，变形可分为瞬时变形和流变（蠕变）两部分，变形与堆石料、接触面和面板连接缝有关，应针对不同情况选取相应的计算模型。

2 反演计算模型选择

2.1 筑坝材料的应力-应变计算模型

（1）堆石料。堆石料是非线性材料，变形不仅随荷载的大小而变化，还与加荷的应力路径相关，应力应变关系呈现明显的非线性特征［16］。邓肯E-B模型公式简单，参数物理意义明确。三轴试验研究结果表明，其对土体应力应变非线性特征亦能较好地反映，因此，本文选择邓肯E-B模型用作堆石料、沙砾料、垫层和过度料等的本构模型。模型以切线弹性模量Et和切线体积模量Bt作为计算参数，其中切线弹性模量表达式为：

其中S为剪应力水平，反映材料强度发挥程度，表达式为：

（σ1-σ3）f为破坏时的偏应力，由摩尔-库伦（Mohr-Coulomb）破坏准则，可得：

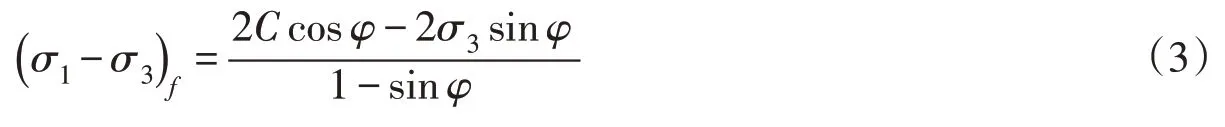
切线体积变形模量为：

对于卸载情况，采用回弹模量Eur进行计算：

加载准则根据计算的单元应力水平和偏应力规定，满足下式条件时采用卸荷模量：

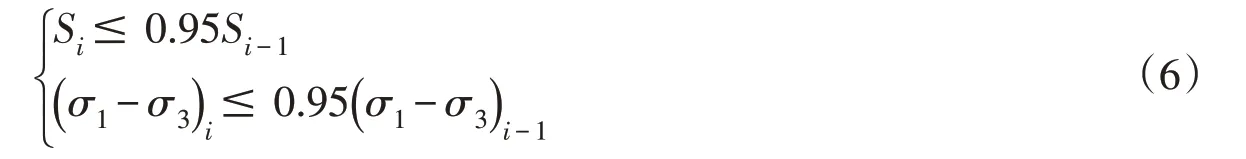
由于邓肯E-B模型是针对二维问题提出的，在三维计算中，以广义剪应力q代替(σ1-σ3)f，以平均主应力p代替σ3，将其推广到三维问题。根据三维问题的摩尔-库伦准则，破坏偏应力(σ1-σ3)f表示为：

其中θσ为Lode应力角，按下式计算：

堆石料的强度在一定程度上表现出非线性，以下式考虑粗粒料内摩擦角φ随围压σ3的变化：

上述各式中：Pa为单位大气压力；C、φ0、Δφ、K、n、Rf、Kb、m、Kur、nur为模型参数，由常规三轴试验得出。

（2）接触面。面板堆石坝中混凝土面板与垫层料的刚度差异较大。在外荷载作用下，两种材料在交接部位的变形可能存在不连续现象。为模拟两种不同材料间的相互作用，进行有限元分析时，设置Goodman接触面单元处理这种位移不协调问题。

克拉夫和邓肯应用直剪仪对于不同材料接触面上的摩擦特性进行试验研究的结果表明，接触面上剪应力τ与相对位移ws呈非线性关系，可近似表示呈双曲线形式，其切线剪切劲度系数可表达为：

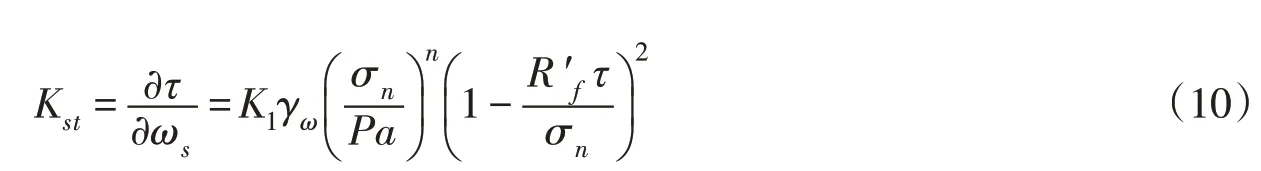
三维非线性分析中无厚度接触面单元的两个切线方向劲度为：

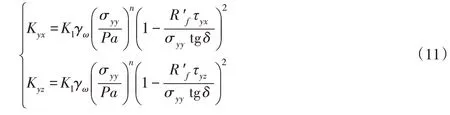
式（10）—式（11）中：K1、n、为模型试验参数；δ为接触面的摩擦角；γw为水的容量；Kyy为法向劲度系数，当接触面受压时取较大值（如Kyy=1083），当接触面受拉取较小值（如Kyy=103）。

（3）面板连接缝。混凝土面板与面板之间以及面板与趾板之间的接缝中，设有铜片以及玛蹄脂等各种止水材料，计算时采用无厚度的连接单元模拟接缝之间的相互作用。分析时不考虑接触面法向应力和剪应力与法向相对位移和切向位移之间的耦合作用。相应方向的劲度模量由接缝止水材料的试验确定。采用河海大学结合水布垭工程研究得出的用于连接单元分析的力与相对位移的关系式［17］，见表1。

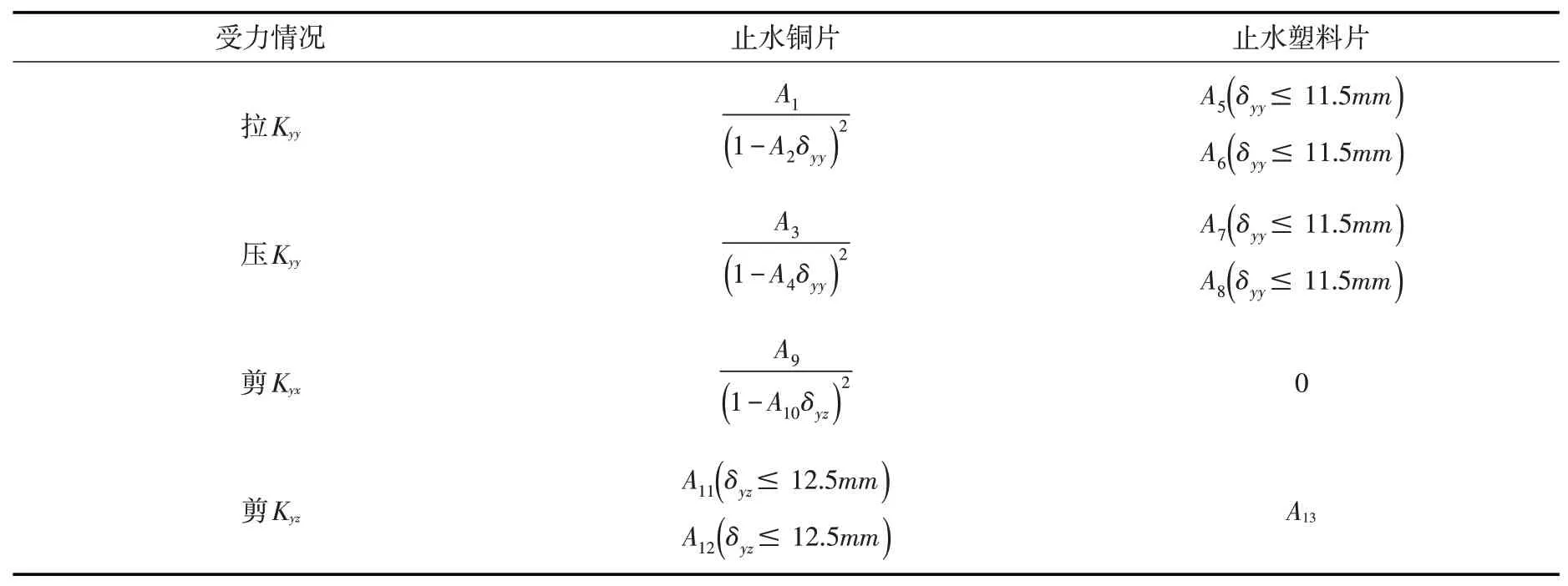
表1 连接单元进度表达式

2.2 堆石料流变计算模型堆石料流变计算采用表达简便、参数物理意义明确的指数型流变模型。将堆石变形与时间关系拟合为指数函数：

相应的应变速率为：

式中：εf相当于t→∞时的最终流变量；c相当于t=0时第一天流变量占εf的比值。

沈珠江根据试验结果进行分析得出：最终体积流变量εvf与围压σ3成正比，最终剪切流变量与应力水平有关，并建议如下关系式：

式中：b为σ3=Pa（大气压）时的最终体积流变量；d为应力水平S1=0.5时的最终剪切流变量。

破坏时S1=1，εsf→∞。计算时，如S1≥1时，可限定S1=0.95。

假定堆石料的体积流变与剪切流变均可用式（14）和式（15）描述，则体积流变速率和剪切流变速率分别为：

依据以上体积与剪切流变特性的规律，采用Prandt1-Reuss 流动法则，按塑性力学的处理方法，应变分量的流变速率写为：

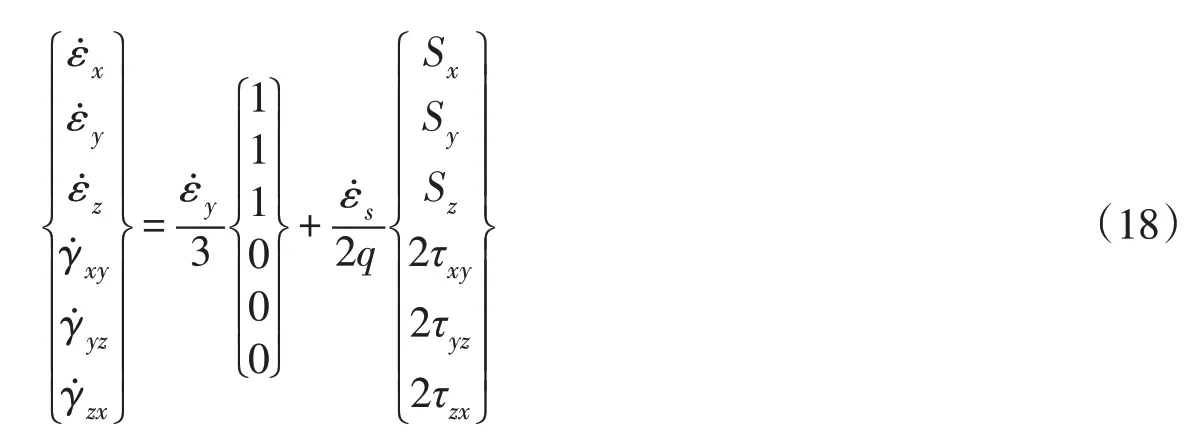
式中：Sx、Sy、Sz为偏应力；q为八面体剪应力。

3 面板堆石坝变形参数反演

3.1 工程概况双沟水电站位于吉林省抚松县境内、第二松花江上游松江河上，枢纽由混凝土面板堆石坝、岸坡溢洪道和引水发电系统组成。面板堆石坝最大坝高110.5 m，坝顶长294 m，坝顶高程590 m，大坝下游面514、539和564 m高程设置了3条马道。水库死水位567 m，正常蓄水位585 m，水库总库容3.88×108m3，电站总装机2×140 MW。

工程于1997年开工，2004年11月大江截流、主体工程全面开工，2005年11月坝体填至494 m高程，2006 年11 月填至540.2 m 高程，2007 年10 月坝体填至586 m 设计高程，2008 年5 月开始进行混凝土面板施工，2008 年10 月完成。2009 年8 月15 日水库开始蓄水，2010 年3 月9 日蓄水至死水位，2010年4月两台机组投产发电。

大坝设置了内、外部变形监测系统。外部变形观测包括大坝水平位移与垂直位移，水平位移采用视准线按活动觇标法观测，共布设5条视准线：坝顶及下游3层马道各布置1条、坝体上游面板正常蓄水位以上布置1条，共设置了28个观测点；大坝垂直位移通过设置的垂直位移观测点采用精密水准仪和配套的铟钢条码尺进行观测。内部变形观测包括堆石体内部水平位移和垂直位移监测，采用埋设土体位移计和沉降仪进行观测，以3 条马道所在高程（514 m、539 m、564 m）作为监测高程，每条马道布置1条测线，分别布置了6个、4个、3个测点，共13个测点进行监测。

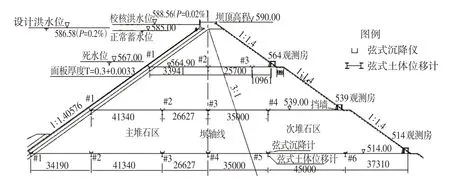
图1 0+190.35监测断面仪器布置（高程单位：m；水平距离单位：mm）

3.2 大坝的实际加载过程与模拟考虑到坝体施工分层填筑的特点和堆石的非线性特性，荷载采用逐级施加的方式模拟实际施工过程，按坝体施工填筑高程共分14级：第1级模拟施加河床地基覆盖层与岸坡强风化安山岩基，第2～13级堆石体坝体填筑至586 m；第14级坝体填筑至586 m到混凝土面板施工前。

3.3 大坝堆石体有限元计算网格剖分为模拟大坝填筑加载过程，对大坝进行有限元计算分析的网格剖分，共剖得单元数6837个，总节点数9224个。计算网格见图2。

3.4 筑坝堆石体瞬时变形计算参数选取大坝瞬时变形参数选取设计阶段拟定的计算参数，见表2。

3.5 堆石体流变参数反演考虑到式（14）是在低应力下整理的结果，对于双沟面板坝，改用下式反映高围压对最终体积流变的影响：

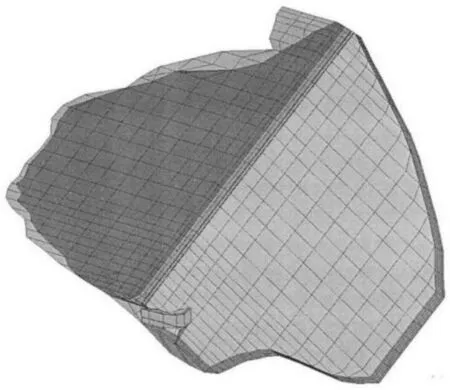
图2 计算网格剖分

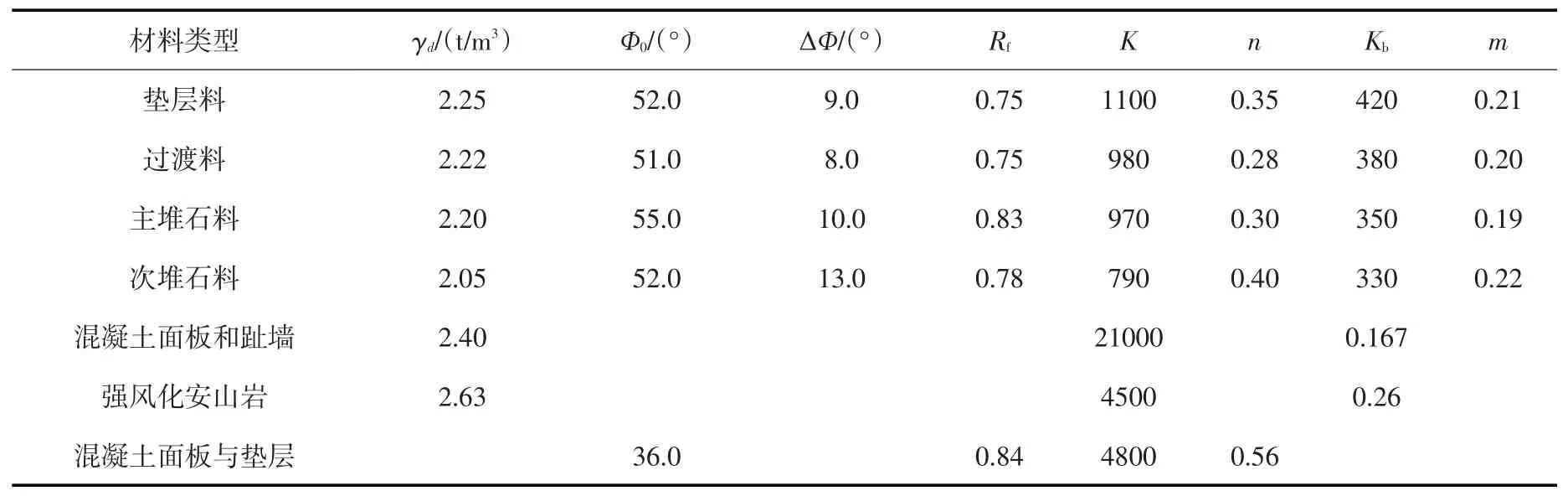
表2 筑坝材料E-B模型的分析拟定参数

采用室内试验成果计算大坝的瞬时变形，将原型实际监测变形按瞬时变形和流变变形进行分离，然后反演流变模型参数。

（1）堆石流变量的分离及流变时段的选取。大坝现场实际测量的变形观测值包括瞬时变形和流变变形分量，两者相互耦合。为了尽量排除自重等外荷载所引起的瞬时变形分量的干扰，从堆石体总变形中合理分离流变变形，通过反演分析获取较为准确的筑坝材料的流变参数。选择大坝停工阶段或者大坝竣工后外荷载基本不变的时期，此时堆石的瞬时变形已经完成，分离流变变形的可信度较高，反演分析得出的流变参数较为合理。

分析双沟大坝的施工加载过程发现，堆石体基本上为全断面填筑，在2006 年11 月13 日填筑到539 m高程后暂停施工至2007年4月初，期间坝体所受外荷载没有变化，测点在该时段内的沉降主要来自流变分量，堆石流变参数的反演目标就以该时段内514 m高程的6个测点的计算流变与实测流变组合成目标函数来反演堆石体的流变参数。

（2）堆石料流变参数的反演分析。对照大坝监测资料与已有参数研究资料初步确定3个流变参数范围（见表3）作为约束条件，然后利用免疫遗传算法反演坝体材料的参数b、c、d、nl值，以选定时段中的测点实测位移增量和计算位移增量差值的二范数为目标函数来寻优，分别反演主堆石和次堆石的流变参数，见表4。

3.6 堆石体E-B模型目标函数与反演参数的选取土石坝筑坝原型观测资料瞬时力学参数的反演采用有限元法计算分析，通过原型观测点的实测变形值和计算变形值，构筑目标函数，成为IGA（Im⁃mune Genetic Algorithm）抗原。考虑到观测仪器在埋设初期受施工因素干扰较大，目标函数采用分时段计算；同时，为了平衡大小值之间作用和消除变形、应变或应力值等不同物理量的量纲，建立目标函数如下：

表3 流变参数变化范围

表4 反演所得流变参数

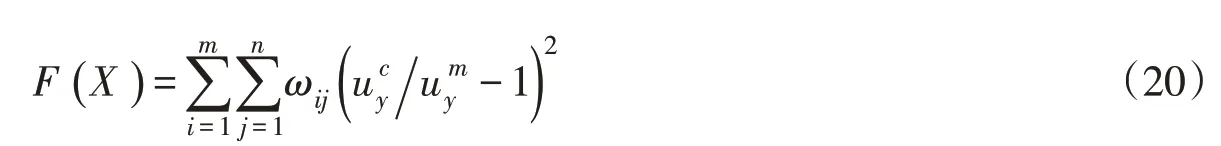
式中：m为反演分析所选取的计算时段总数；n为选取观测点总数；ωij为在第i个时段第j个测点量测值的权重；为第i个时段第j个测点对应某级荷载组合作用时的计算变形、应变或应力值；为相应的实测值。

筑坝材料的容重、孔隙比、强度等基本特性参数现场可以直接测量。应力-应变本构模型参数—邓肯非线性模型参数见式（21），则自变量X对应备选抗体：

参考坝料室内三轴试验资料，选取参数X估计范围［18］（见表5）成为IGA 的初始搜素范围，即式（21）的约束条件。

反演得到的邓肯E-B模型参数结果见表6。

表5 堆石体E-B模型参数的变化范围

表6 大坝主堆石区和次堆石区的反演结果

4 反演计算结果与原型实际监测值对比分析

4.1 施工期利用大坝原型实测资料，选择堆石体填筑到坝顶586 m高程时（2007年10月15日）对应的3个监测断面514、539和564 m高程沉降仪测点处的计算值与观测值对比，对大坝堆石料的反演参数进行校验分析。

（1）累计全量分析。大坝施工至586 m高程时，514、539和564 m高程各测点沉降计算值与观测值对比见图3—图5。

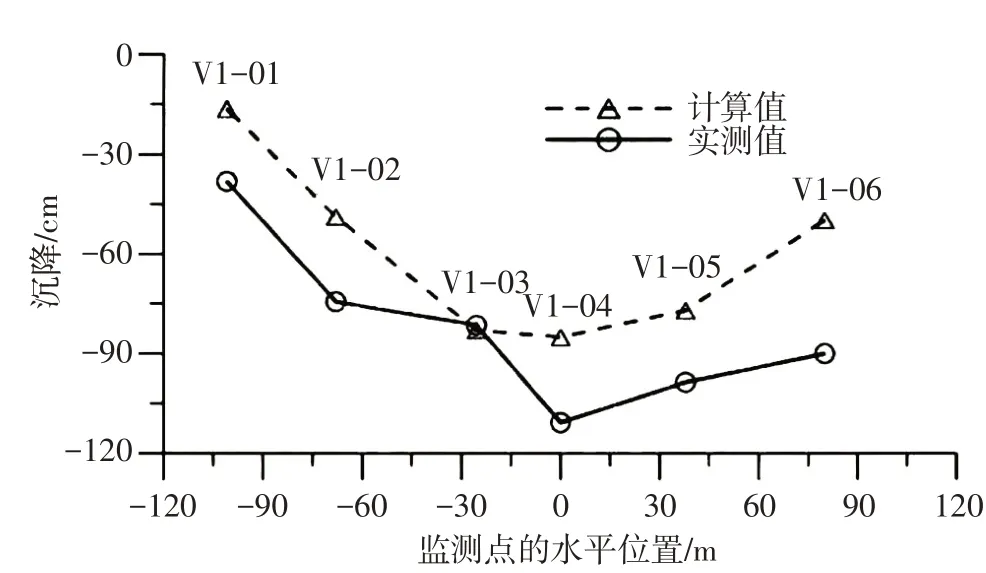
图3 2007年10月15日514 m高程监测点竖向位移分布

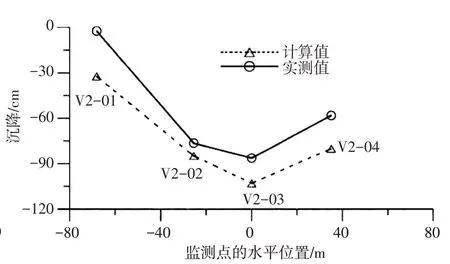
图4 2007年10月15日539 m高程监测点竖向位移分布

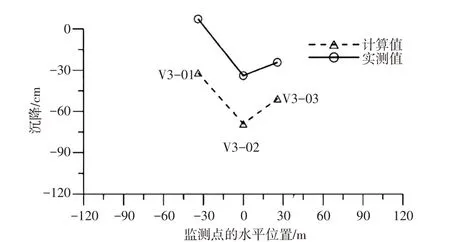
图5 2007年10月15日564 m高程监测点竖向位移分布

从图中可以看出，计算值与观测结果分布规律一致。反演参数对应的堆石体变形计算值在514 m高程较实测值偏小，在539 m和564 m高程较实测值偏大，分析其原因：514 m高程的监测仪器在施工中发生过损坏，经过处理后继续观测，继续观测时对该高程实测过程线进行了修正；各高程监测到的沉降值均是相对于观测房的相对沉降值，由于观测房本身也存在随时间下沉问题，因此各高程的监测沉降值均存在不同程度漏测，导致实测的沉降值小于计算值。

（2）增量分析。为了避免漏测和施工误差的影响，采用增量分析来检验反演参数的合理性。选取2007 年7 月22 日坝体填筑至570 m 高程为起点，以2007 年10 月15 日坝体填筑至586 m 高程为终点，进行大坝的第一时段增量分析；选取2008年1月20日为起点，2008年3月4日为终点，进行大坝第二时段的增量分析。

第一时段514和539 m高程沉降增量反演计算值与实测值对比见表7、表8。

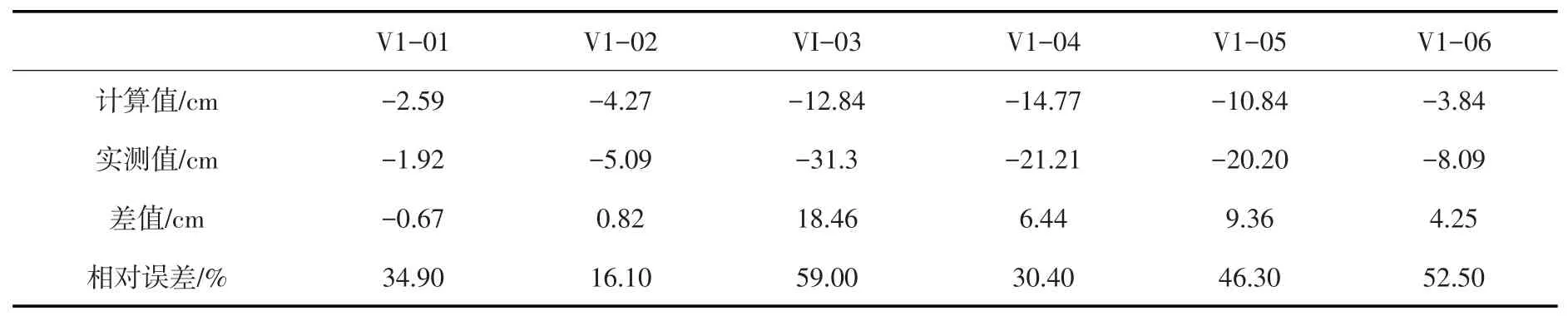
表7 514 m高程沉降观测值与计算值对比

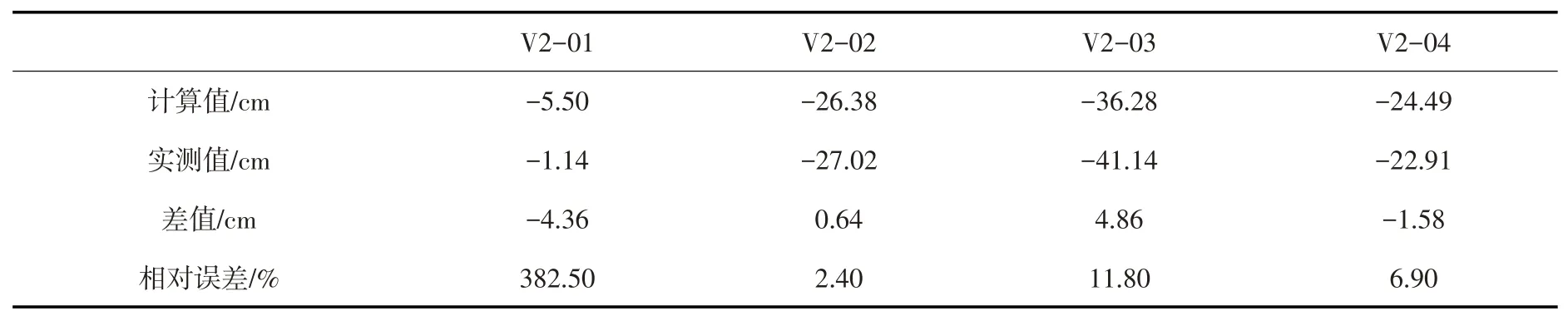
表8 539 m高程沉降观测值与计算值对比

第二时段514和539 m高程沉降增量反演计算值与实测值对比见表9、表10。

表9 514 m高程沉降观测值与计算值对比

表10 539 m高程沉降观测值与计算值对比

从增量分析结果看，第一时段514 m高程计算值与实测值变化趋势一致、相对误差较大，539高程计算值与实测值变化趋势一致、相对误差总体较小；第二时段514 m高程计算值与实测值部分测点变化趋势一致、相对误差较大，539 m高程计算值与实测值变化趋势基本一致、相对误差总体较小。个别偏离较大的测点为设备误差或施工影响导致。

4.2 运行期利用反演分析得出的瞬时变形参数与流变特性参数，采用邓肯E-B模型计算水库蓄水运行3年后大坝的变形极值，并将计算值与实测值进行对比，见表11。

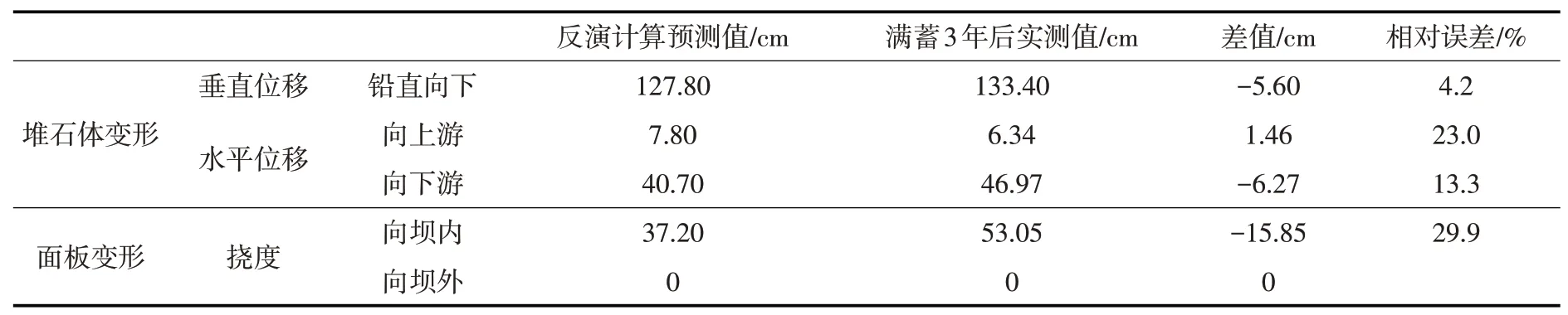
表11 水库蓄水运行3年后反演计算预测值与实测值对比

水库满蓄运行3年后的反演计算值与实测值相比，垂直位移相差5.60 cm，向上游水平位移相差1.46 cm、向下游水平位移相差6.27 cm，面板挠度实测最大值大于计算值15.85 cm。堆石体垂直位移、水平位移及面板挠度反演值与实测值比较接近，相对误差较小。

5 结论

利用反演所得到的流变参数和坝体材料参数进行有限元计算，基本上能有效地反映填筑加荷对坝体沉降的响应，模拟出大坝的实际沉降情况，反应坝体沉降规律。

施工期，坝体内部沉降计算值与观测值分布规律总体一致。通过累计全量计算值与实测值对比分析，反映出各高程沉降监测值存在不同程度的漏测问题。增量分析结果显示，514 m高程计算值与相应的实测值相对误差除个别测点外均在20%以上、相对较大，为设备误差或施工影响导致；539 m高程计算值与相应的实测值相对误差除个别测点外均在20%以下、相对较小。

水库蓄水运行3年后，大坝堆石体实测内部变形与反演计算值吻合较好，变化趋势一致，误差在4.2%～29.9%之间，相对较小。计算值基本反映了大坝实际运行状况。