基于人工免疫算法的离散隐马尔科夫故障诊断模型优化

张小强，朱文辉，康铁宇，黄晋英

（1.北京北方车辆集团有限公司，北京 100072；2. 中北大学 机械工程学院，太原 030051）

行星齿轮箱结构紧凑、传动比大、传动平稳，广泛应用于风电机组、直升机传动系统等领域，工作过程中运行工况变化范围大，齿轮、轴承等零部件往往承受着较大负载，容易出现损伤进而影响到行星齿轮箱的正常工作，因此对行星齿轮箱进行早期故障诊断具有重大的意义。现有的行星齿轮箱故障诊断多从动力学建模和动态信号处理的角度两方面进行，冯志鹏、褚福磊等[1-3]针对行星齿轮箱的齿轮局部故障和分布式故障的振动特征开展了一系列研究。雷亚国等[4-5]针对行星齿轮箱故障诊断中的多传感器信息融合、动力学新模型的故障响应特性等开展了研究。

隐马尔科夫模型是一种动态模式识别方法，利用历史数据和当前数据对研究对象进行建模，最初运用于语音识别领域，取得了较好的效果。将隐马尔科夫模型引入机械系统的故障诊断中，其建模过程实质上就是参数估计问题。故障诊断隐马尔可夫模型初始观测矩阵的选择对诊断效果影响较大，目前对初始观测矩阵的选择还没有指导性的方法，这个问题也成为该方法用于故障诊断的研究热点之一。袁洪芳等[6]将粒子群优化算法用于离散隐马尔可夫模型初始观测矩阵的优化，并在滚动轴承的故障工况上进行了验证。陈玄等[7]采用支持向量机的方法对初始观测矩阵进行估计，并应用到轴承的故障诊断中，取得了较好的效果。何栋磊、周金祖采用遗传算法对初始观测矩阵进行优化，分别将优化后的隐马尔科夫模型用于电路板和轴承的故障诊断中[8-9]。

上述研究成果多采用单一样本设置目标函数，在达到结束条件后，选择目标函数值最大时的初始观测矩阵作为最优观测矩阵，适用于故障特征明显的诊断问题。当不同工况下的故障特征微弱时，采用上述方法容易导致模型退化。文中采用人工免疫算法对初始观测矩阵进行寻优，将包含易被误判样本的优化集作为抗原，以优化集整体的识别率为目标函数、待优化的初始观测矩阵为抗体对其进行优化，建立改进的离散隐马尔科夫模型，并在三种工况下的行星齿轮箱上进行了验证。

1 DHMM模型

隐马尔科夫模型由马尔科夫链和随机过程构成，马尔科夫链用来描述研究对象不同状态的转移关系，随机过程用来描述观测值的变化。离散隐马尔科夫模型（Discrete Hidden Markov Model，DHMM）是隐马尔科夫模型的一种，其观测到的随机变量的统计变量是离散的。行星齿轮箱的DHMM模型可用式（1）表示：

式中：N为模型的隐状态数；M为每个状态对应的可能的观测值数目；A为状态转移概率矩阵；B为观测值概率矩阵；π为初始状态概率分布矢量。

N个状态分别记为 S1,S2,…,SN，记 t时刻 HMM所处状态为 qt，qt∈(S1,S2,…,SN)，文中将行星齿轮箱的故障类型数目定义为其隐状态数。M个观测值分别为 v1,v2,…,vM，记 t时刻观测到的值为 ot，ot∈(v1,v2,…,vM)。

状态转移概率矩阵A为：

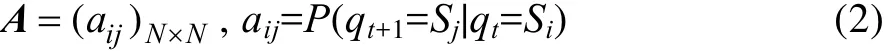
观测值概率矩阵B为：

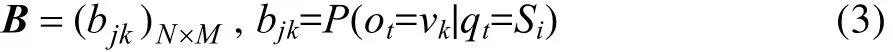
运用中，初始状态概率π往往是随机给定的。当状态转移矩阵、观察值概率矩阵和初始状态矩阵确定了，DHMM模型也就确定了。

对于给定了观测值序列(o1,o2,…,ot)的 DHMM 模型的建立，即 DHMM 参数估计问题。常常采用Baum-Welch重估公式来确定模型λ。测概率矩阵中的元素bjk即为状态j下观测到vk的概率。

初始状态概率分布矢量 π=(π1,π2,…,πN)，其中πi=P(q1=Si)。

2 故障诊断步骤

1）数据采集。在行星齿轮箱相应位置设置测点，采集齿轮箱各工况下的振动信号。

2）特征提取。采用一定的信号处理方法提取特征，视情况对特征进行约减、降维等以去除冗余信息、降低后续建模和诊断的计算量。

3）各工况DHMM模型的建立。将训练样本的特征集用Baum-Welch算法[10]估计HMM模型的各个参数，直到达到停止条件。

4）故障诊断。对测试样本采取维特比算法求取该特征在各模型下的最大似然概率，比较各个概率值的大小，最大值对应的故障模式即为其最有可能的状态，从而完成故障诊断。

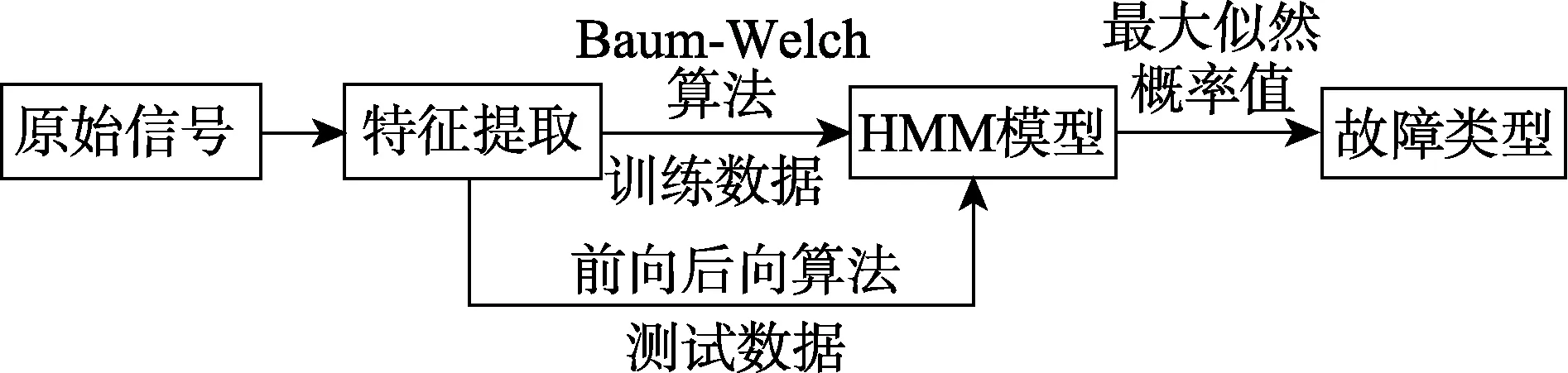
图1 隐马尔科夫模型故障诊断流程

3 初始观测矩阵的优化

人工免疫算法可以看作是人工免疫理论和遗传算法的结合，解决了遗传算法的早熟收敛问题。相比于遗传算法，人工免疫算法中，抗体具有更好的多样性、更强的局部搜索能力和更快的搜索速度[11]。免疫系统、基于人工免疫算法的观测矩阵优化算法中变量对照关系见表1。

表1 变量对照关系

基于人工免疫算法的初始观测矩阵优化的流程如图2所示。

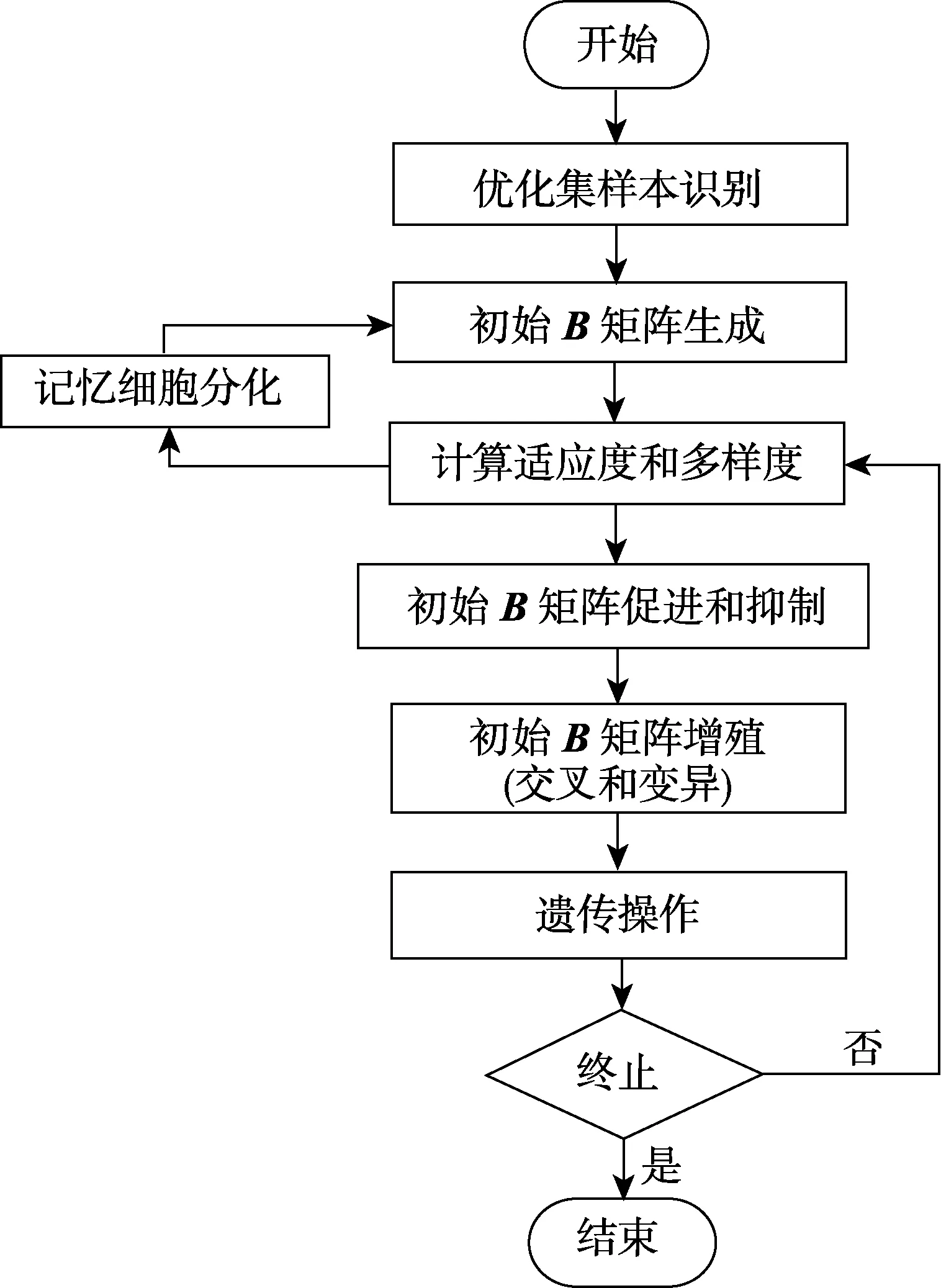
图2 基于人工免疫算法的初始观测矩阵优化的流程

针对单一样本进行优化时，常采用的目标函数是该样本在已建立模型下的概率，即：

当单一样本是该工况下的典型样本时，优化后的模型可能对典型样本的识别精度更高，对非典型样本的识别精度下降；当单一样本是非典型样本时，优化后的模型对与其类似的非典型样本的识别精度较高，而该工况下的其他样本识别精度下降。倘若采用单一样本进行优化，以上两个问题无法避免，必居其一。因此，这里采用多样本进行优化，构造一个包含典型样本和非典型样本的优化集，求其各样本在对应模型下的概率对数之和，当和越大，则认为优化后的模型更优，此时的目标函数为：

4 实验验证

在行星齿轮箱故障诊断实验台（如图3所示）上进行了实验，该实验台主要由变频电机、斜齿轮箱、联轴器、行星齿轮箱和磁粉制动器等构成，采集系统为美国晶钻仪器公司的 Coco-80X便携式动态采集仪。仅对行星齿轮箱的故障进行了分析。在箱体上，对应行星架的部位四周设置了五个振动加速度传感器，在行星轮输入轴轴承座上方设置了一个振动加速度传感器，针对太阳轮设置了正常、断齿和磨损三种工况，如图4所示。采样频率设置为10.24 kHz，采集齿轮箱转速为 900 r/min，磁粉制动器负载电流为0.3 A时箱体的振动信号。

图3 行星齿轮箱故障诊断实验台

图4 太阳轮

以齿轮箱顶端的三向加速度传感器的z向时域曲线（如图5所示）为例，断齿和磨损工况下的曲线波形区别不明显，三类工况下的振动加速度均方根值差别不大，说明通过波形曲线不能有效诊断齿轮箱的工况。因此，对采集到的数据进行时频分析，提取时域方根幅值、时域绝对平均幅值、频域均方根值等 12个时频特征作为原始特征集，用到的时频特征见表2。每种工况各取90个样本作为DHMM的训练样本，24个样本作为DHMM的测试样本。

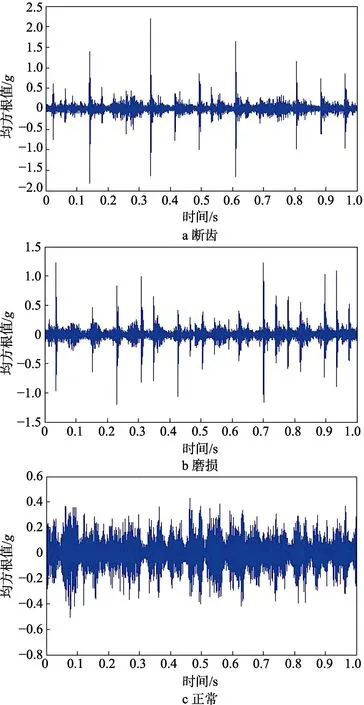
图5 太阳轮5测点z向时域曲线

表2 时频特征

首先利用三种工况下的训练样本对相应工况建立起各自的DHMM模型。由于样本数量有限，这里将训练样本和测试样本一起通过建立好的DHMM进行粗分类，以挑选出各类别中易被误判的样本。然后将各类易被误判的样本与其典型样本一起构造多样本优化集，用于各类模型的优化。优化时，多样本优化集对应于抗原，适应度函数，初始抗体规模设置为100，同时为简化计算量，抗体复制因子设为0.3，迭代代数设置为30。采用多样本优化后的DHMM诊断结果见表3和图6。

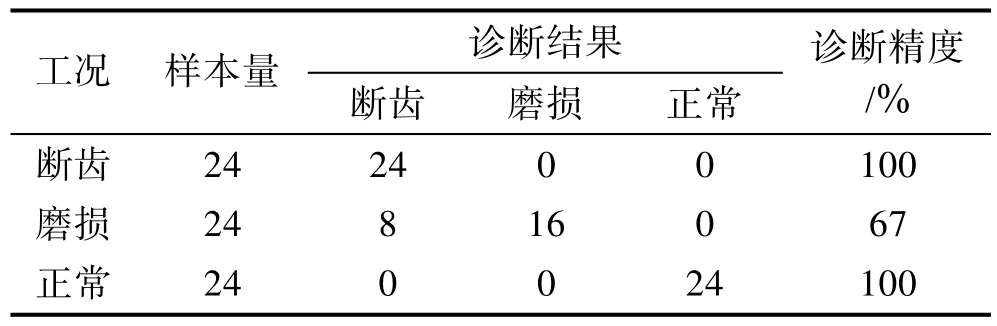
表3 多样本优化后DHMM模型故障诊断结果

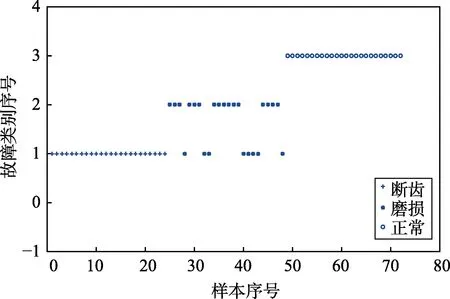
图6 多样本优化后的DHMM故障诊断结果

为进一步比较采用单一样本优化和多样本优化的DHMM分类效果，这里随机选取各类工况下的单一样本作为抗原进行优化，优化时的参数设置与多样本优化时的一样。两种方法优化后的故障诊断结果见表4。可以看出，单一样本优化后的正常工况下的诊断精度相对于多样本下的诊断精度有所下降，微弱故障（磨损）的诊断精度不高，模型需进一步优化。

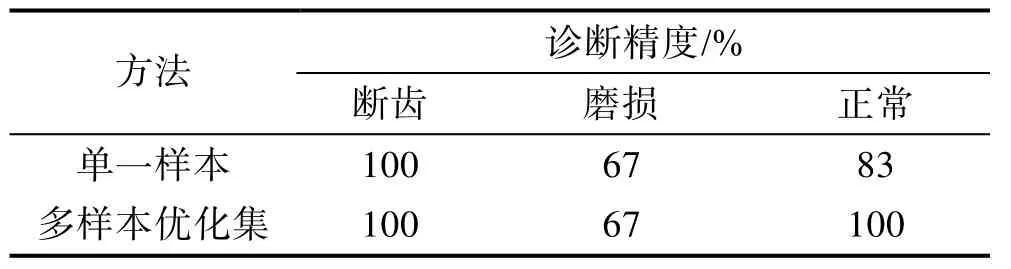
表4 单一样本和多样本优化后DHMM模型故障诊断结果

5 结语

初始观测矩阵的选择对隐马尔科夫模型质量好坏影响较大，进而影响其故障诊断精度。参考文献中提出了基于单一样本的优化方法，文中基于人工免疫算法提出了采用多样本优化的方法，并通过实验验证了该方法的可行性。