基于电化学-热耦合模型研究隔膜孔隙结构对锂离子电池性能的影响机制∗
2019-01-25曾建邦郭雪莹刘立超沈祖英单丰武罗玉峰
曾建邦 郭雪莹 刘立超 沈祖英 单丰武 罗玉峰
1)(华东交通大学材料科学与工程学院,江西省轨道交通关键材料工程技术研究中心,南昌 330013)
2)(江西江铃集团新能源汽车有限公司,南昌 330013)
3)(中国科学院广州能源研究所,中国科学院可再生能源重点实验室,广州 510640)
4)(重庆大学动力工程学院,低品位能源利用技术及系统教育部重点实验室,重庆 400044)
(2018年9月17日收到;2018年10月24日收到修改稿)
隔膜孔隙结构对锂离子电池性能具有重要的影响,本文提出了可准确描述充放电过程中锂离子电池内部复杂物理化学现象的电化学-热耦合模型,发现该模型较文献中模型的计算结果更接近实验测试数据.利用该模型探讨了隔膜孔隙率与扭曲率分别对锂离子电池性能的影响规律,发现减小孔隙率或增大扭曲率,电池输出电压、最大放电容量和平均输出功率均不断降低,电池表面温度和温升速度均不断升高;当孔隙率减小或扭曲率增大到一定程度时,放电初期电池输出电压均会出现先下降后回升的现象,且孔隙率越小或扭曲率越大,其下降的幅度越大、速度越快,回升所需时间也越长;要确保其不低于截止电压,隔膜扭曲率必须小于临界扭曲率(其下降至最低点刚好等于截止电压时的隔膜扭曲率).综合分析了放电过程中电池内部各电化学参量和产热量的动态分布规律,发现隔膜孔隙率和扭曲率主要影响放电末期电极膜片内部电化学反应以及其他放电时刻电解液中有效Li+扩散(传导)系数.
1 引 言
具有孔隙结构特征的隔膜是锂离子电池的重要组件,其性能直接决定电解液的保持性以及电池界面结构和内阻等,进而影响电池容量、功率、安全和循环寿命等,除了需要具备隔离正负极膜片以阻隔电子、吸收电解液以导通Li+等基本作用之外,还应具备良好的化学稳定性、热稳定性、空间结构稳定和平整性以及足够的机械强度(穿刺和拉伸强度)等特殊功能[1,2].可见,锂离子电池性能不仅与制备隔膜所用材料物性相关,而且还与隔膜孔隙结构密切相关.因此,深入研究隔膜孔隙结构对锂离子电池性能影响机制具有重要的现实意义.
近年来,研究人员利用实验测试和数值模拟等手段在揭示隔膜孔隙结构对锂离子电池性能影响机制方面开展了大量的研究工作.在实验测试方面:Venugopal等[3]对隔膜孔隙率和平均孔径进行测量,发现这些参数不仅影响隔膜有效离子传导系数,而且还影响锂离子电池热安全性;Djian等[4]对商业化隔膜孔隙率、孔径分布以及扭曲率等参数进行测试,发现这些参数是降低隔膜有效离子传导系数的重要原因;高洪森等[5]以具有不同孔隙结构的商业化隔膜制备锂离子电池,并对其充放电性能进行测试,发现采用孔隙率约为45%以及孔径分布均匀的隔膜制备的锂离子电池循环性能更为优良;Costa等[6]除了测试隔膜孔隙率和孔径分布之外,还对隔膜机械强度、电解液吸收率以及有效离子传导系数等参数进行了测试,发现孔隙率不仅影响隔膜有效离子传导系数,而且还影响隔膜机械强度和电解液吸收率;在Costa等[6]研究工作的基础上,Plaimer等[7]进一步阐述了孔隙率与隔膜机械强度和有效离子传导系数之间的关系,发现隔膜有效离子传导系数随孔隙率的增大而增大,但当孔隙率增大到一定程度时其机械强度却不断降低;Lee等[8]不仅对采用同样工艺参数制备而成的隔膜孔隙率、透射率、扭曲率、孔径分布、机械强度、Gurley数、电解液吸收率和有效离子传导系数等参数进行测试,而且还对以其制备的锂离子电池容量、循环寿命等性能进行测试,发现隔膜平均孔径、透射率、电解液吸收率和有效离子传导系数以及以其制备的锂离子电池容量和循环寿命等均随孔隙率的增大而增大,而隔膜Gurley数和扭曲率则随孔隙率的增大而减小.从上述研究成果来看:实验测试还难以明确隔膜孔隙结构对锂离子电池性能的影响规律,主要原因是实际制备隔膜过程难以确保单一孔隙结构参数(如孔隙率、孔径分布或扭曲率等)变化时其他孔隙结构参数不受影响.可见,实验测试在揭示隔膜孔隙结构对锂离子电池性能影响机制方面几乎无能为力.
然而,明确电极膜片/隔膜孔隙结构对锂离子电池性能的影响机制是电极膜片/隔膜孔隙结构优化设计的基础和前提.近年来,随着计算机技术和数值计算技术的飞速发展,数值模拟作为一种重要的手段或工具在电极膜片/隔膜孔隙结构优化设计方面具有巨大的潜力[9-11].Newman研究组[12-14]发现对正极膜片孔隙率或厚度进行优化设计可提高电池功率或能量密度;Appiah等[15]发现对正极膜片孔隙率或厚度进行优化设计均可延长电池放电时间;De等[16]发现同时对正极膜片孔隙率和厚度进行优化设计可最大限度的提高电池比能量.Golmon等[17,18]发现同时对正极膜片孔隙率和活性物颗粒尺寸进行优化设计可最大限度地提高电池容量;Miranda等[19]发现对隔膜厚度、孔隙率以及扭曲率等孔隙结构参数进行优化设计可降低电池内阻、提高电池输出电压和最大放电容量;Xue等[20]发现对正负极膜片厚度、质量比、孔隙率和活性物颗粒尺寸,隔膜厚度及相关传输系数等参数进行优化设计,可在不同放电策略下最大限度地提高电池质量能量密度.Liu等[21]发现对正负极膜片厚度、活性物颗粒尺寸以及孔隙率等孔隙结构参数进行优化设计,不仅可以减小电池容量衰减速度,而且还可最大限度地提高电池比能量和比功率.从上述研究成果来看:目前研究人员的精力主要集中在电极膜片孔隙结构的优化设计,较少关注隔膜孔隙结构对锂离子电池性能的影响机制,且已有的研究成果均是基于锂离子电池电化学模型模拟的结果.
为此,本文提出了可以更加准确地描述充放电过程中锂离子电池内部复杂物理化学现象的电化学-热耦合模型,并结合文献中的实验测试和数值模拟结果对模型进行验证;然后,利用验证后的模型探讨隔膜孔隙率和扭曲率分别对电池放电曲线、表面温升曲线以及最大放电容量和平均输出功率等性能的影响规律;最后,结合放电过程中电池内部各电化学参量和产热量的动态分布信息,深入揭示隔膜孔隙率和扭曲率分别对锂离子电池性能的影响机制.
2 模型构建
2.1 物理模型
本文以如图1所示的LiMn2O4|LiPF6|LiC6电池体系为例,从左至右分别为负极集流体,厚度为L1;负极膜片,厚度为LN;隔膜,厚度为LS;正极膜片,厚度为LP;正极集流体,厚度为L2;L=LN+LS+LP.电极膜片固体骨架由活性物颗粒和添加物制备而成,隔膜固体骨架(既不导电子也不导离子)由聚合物材料制备而成,电极膜片和隔膜孔隙均被电解液(只能导离子)占据.
在放电过程中,电流由负极集流体导入负极膜片固体骨架,如图1所示,在LimC6颗粒与电解液交界面处发生电化学反应:

式中m为放电前负极活性物颗粒内部Li原子数目;d为放电过程中负极活性物颗粒失去的Li原子数目.该反应可将LimC6颗粒表面的Li转变成Li+并溶解于电解液中,导致Lim-dC6颗粒内部与表面间出现浓差现象,进而引发Li从Lim-dC6颗粒中心向外的扩散现象;同时由于该反应生成的Li+进入界面区域附近的电解液中,导致电解液中Li+浓度产生差异,进而引发Li+从界面区域向远离界面区域的扩散与迁移现象.在正极膜片区域,由于Lin-dMn2O4颗粒、电解液中Li+以及经过外电路流入的电子在Lin-dMn2O4颗粒与电解液交界面处结合发生电化学反应:
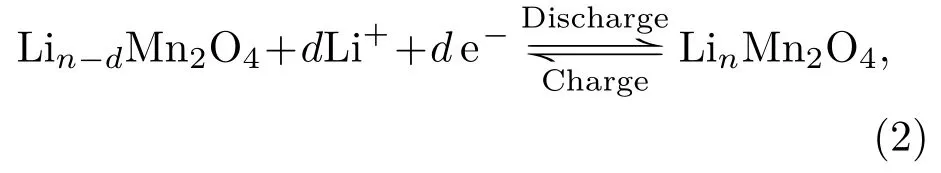
式中n为放电结束时正极活性物颗粒内部Li原子数目.该反应消耗了界面区域附近电解液中的Li+,导致电解液内部Li+浓度产生差异,进而引发Li+从远离界面区域向界面区域的扩散与迁移现象;同时由于该反应将电解液中Li+转化成Li并嵌入Lin-dMn2O4颗粒中,导致LinMn2O4颗粒内部与表面间出现浓差现象,从而引发Li由LinMn2O4颗粒表面向内部的扩散现象.另外,由于正极膜片内部电化学反应消耗电解液中Li+,负极膜片内部电化学反应产生Li+,导致锂离子电池内部电解液中Li+浓度出现差异,从而引发Li+从负极膜片侧穿过隔膜进入正极膜片侧的扩散与迁移现象.充电过程正好与上述过程相反.
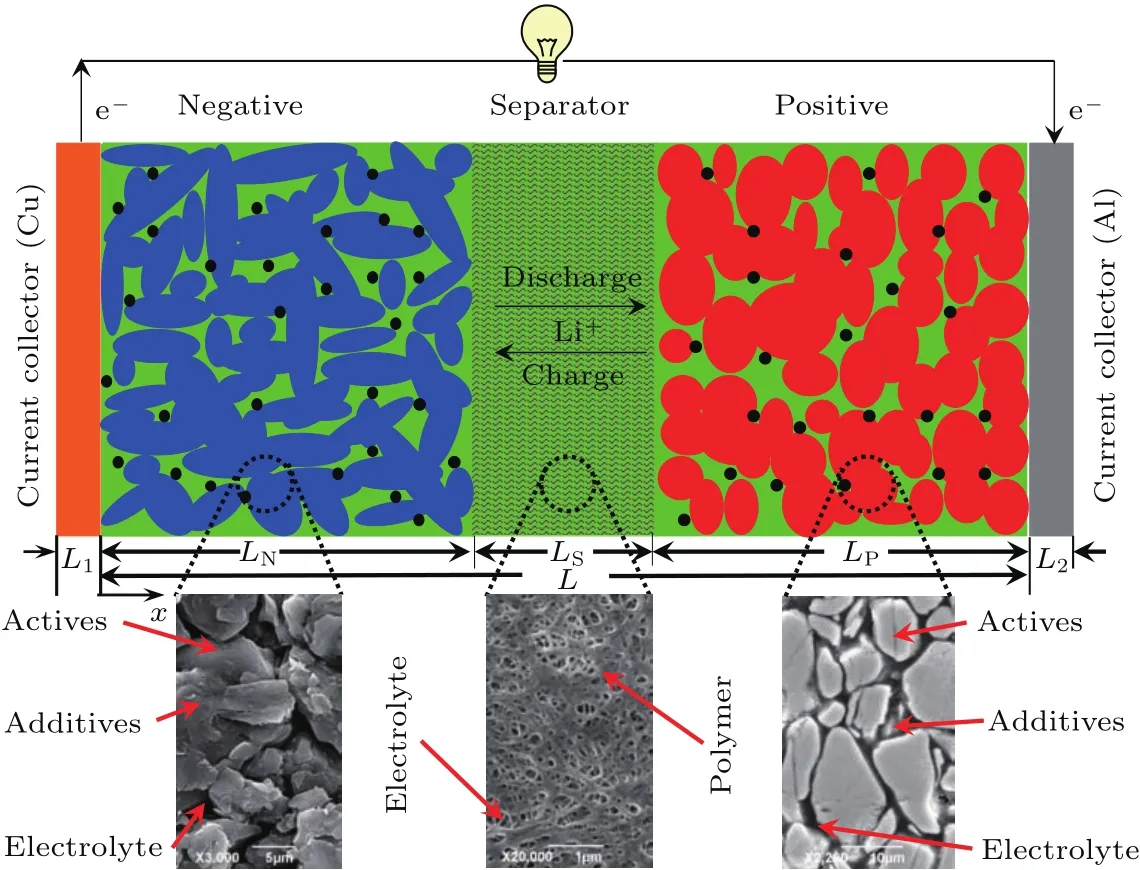
图1 锂离子电池物理模型Fig.1.Schematic of a lithium-ion battery.
2.2 数学模型
基于以上分析可知锂离子电池在充放电过程中,其内部主要发生集流体和电极膜片固体骨架中电子传导现象、活性物颗粒内部Li扩散现象、电解液中Li+扩散与传导现象、活性物颗粒与电解液交界面处的电化学反应现象以及伴随上述现象发生的热产生及传递现象.针对上述复杂的物理化学现象,做如下假设:1)在充放电过程中活性物颗粒体积不变,即电极膜片孔隙率恒定;2)不考虑接触电阻和固体电解质界面(SEI)膜电阻,且充放电过程中不发生副反应;3)电解液和电极膜片内活性物颗粒和添加物颗粒均处于静止状态;4)不考虑集流体对锂离子电池充放电过程中电子传导和热量传输的影响(相比制备电极膜片/隔膜所用材料,制备正、负极集流体所用的铝和铜的电子传导和热传导系数均相对较大).以Newman研究组[12-14]开发的锂离子电池电化学模型为基础,可构建出如表1所列的锂离子电池电化学热耦合数学模型.
表1中ϕs为固相电子电势;σeff为有效电子传导系数;jLi为电化学反应传输流密度;I为放电电流;A为垂直于电池厚度方向(即x方向)的横截面面积;ϕe为电解液中Li+电势;ce为电解液中Li+浓度;κeff和分别为有效Li+传导系数和有效Li+扩散传导系数;cs为活性物颗粒内部Li浓度;Ds为有效Li原子扩散系数;r为活性物颗粒半径方向;ract为活性物颗粒半径;F为法拉第常数;as为电极膜片的比表面积;为有效Li+扩散系数;为离子迁移数;t为放电时间;T为电池内部温度;ρ,Cp和λ分别为混合平均密度、定压比热容以及导热系数;q为热源;h为对流换热系数;Tamb为环境温度.

表1 锂离子电池电化学热耦合模型的控制方程及边界条件Table 1.Governing equations and boundary conditions of the electrochemical-thermal coupled model of a lithium-ion battery.
(5)式中as可根据下式进行估算[22]:

式中εact为电极膜片内部活性物体积分数.
(3)—(6)式中的jLi可根据Bulter-Volmer方程计算得到,
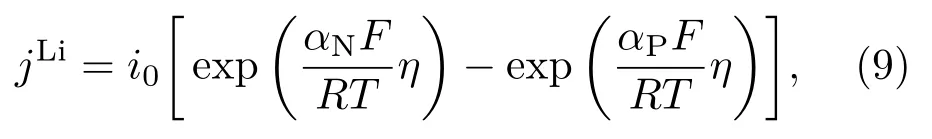
式中R为通用气体常数;αP和αN分别为正、负极膜片的电化学反应传输系数;i0为电化学反应交换流密度;η为过电势,其表达式如下:

式中U为开路势,与荷电状态SOC(活性物颗粒内部局部Li浓度cs与最大Li浓度cs,max的比值)有关.在LiMn2O4|LiPF6|LiC6电池体系中正、负极膜片的开路势U随SOC的变化曲线分别来自文献[23]和[24]中实验测试数据的拟合,见图2.
(9)式中的i0可通过下式计算获得:

式中cs,surf为活性物颗粒表面Li浓度;k为电化学反应速率,与活性物颗粒内部Li的扩散系数Ds一样,均与温度相关,且关联式均满足Arrhenius公式[25]:

式中ψ代表Ds或k;ψref为参考温度Tref下各参数的取值;Eψ为活化能.
以负极混合密度ρ的计算过程为例[26]:

式中i为负极膜片的组分数;εi,ρN,i分别为负极膜片内部组分i的体积分数和密度.类似地,还可计算出正极膜片和隔膜的混合平均密度以及正、负极膜片和隔膜的混合平均定压比热容和热传导系数.另外,(7)式中q可通过下式计算获得:
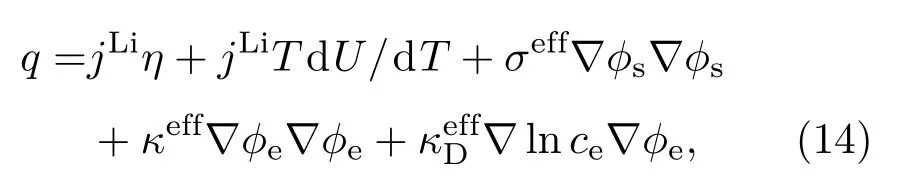
式中右端第一至第五项分别为反应极化热qec、可逆熵热qre、电子欧姆热qeo、离子欧姆热qio和离子迁移热qim.在LiMn2O4|LiPF6|LiC6电池体系中正、负极膜片内部qre中的熵系数dU/dT随SOC的变化曲线分别来自文献[27]和[28]中实验测试数据的拟合,如图3所示.
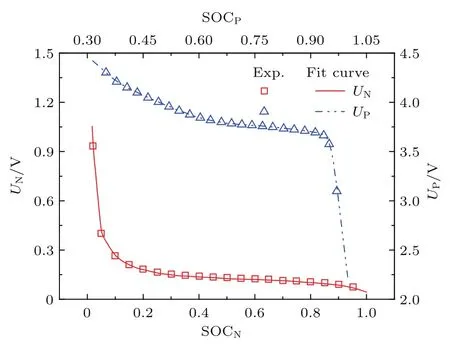
图2 LimC6负极膜片和锰酸锂正极膜片开路势Fig.2.Open circuit voltage of lithiated-carbon negative electrode UNand lithium-manganese-oxide positive electrode UP.

图3 LimC6负极膜片和锰酸锂正极膜片熵系数Fig.3.Entropy change of lithiated-carbon negative electrode dUN/dT and lithium-manganese-oxide positive electrode dUP/dT.
(3),(4),(6)和(14)式中有效扩散(传导)系数的定义如下[19,29-34]:

式中B为布鲁格曼系数,在宏观均质模型中通常取1.5,这与实际电极膜片/隔膜布鲁格曼系数的取值不符[19,27];ε和τ分别为相应相的体积分数和扭曲率,对于电解液相(或电极膜片/隔膜固体骨架)而言,τ为多孔电极膜片/隔膜内部有效孔洞(或骨架)长度与电极膜片/隔膜厚度之比,可反映Li+(或电子)在电极膜片/隔膜孔隙网络内输运路径的扭曲程度[29-34];φ代表电极膜片固体骨架中的电子传导系数σ以及电解液中Li+扩散系数De和Li+传导系数κ.
在LiMn2O4|LiPF6|LiC6电池体系中,电解液中Li+扩散系数De随温度T和电解液中Li+浓度ce的变化曲线来自文献[35]中实验测试数据的拟合,见(16a);而电解液中Li+传导系数κ随温度T和Li+浓度ce的变化曲线则是同时对文献[35]和[36]中实验测试数据的拟合结果,如(16b)和图4所示.从图4中可看出:相比文献[35],[36]和[37]中的拟合曲线,同时对文献[35]和[36]中的实验测试数据进行拟合可更加准确地获取电解液中Li+传导系数κ随温度T和Li+浓度ce的变化曲线.

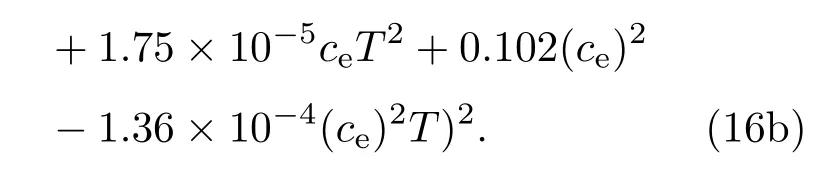
此外,根据(15)式还可计算出κeff,进而可推导出的表达式如下[23,35]:

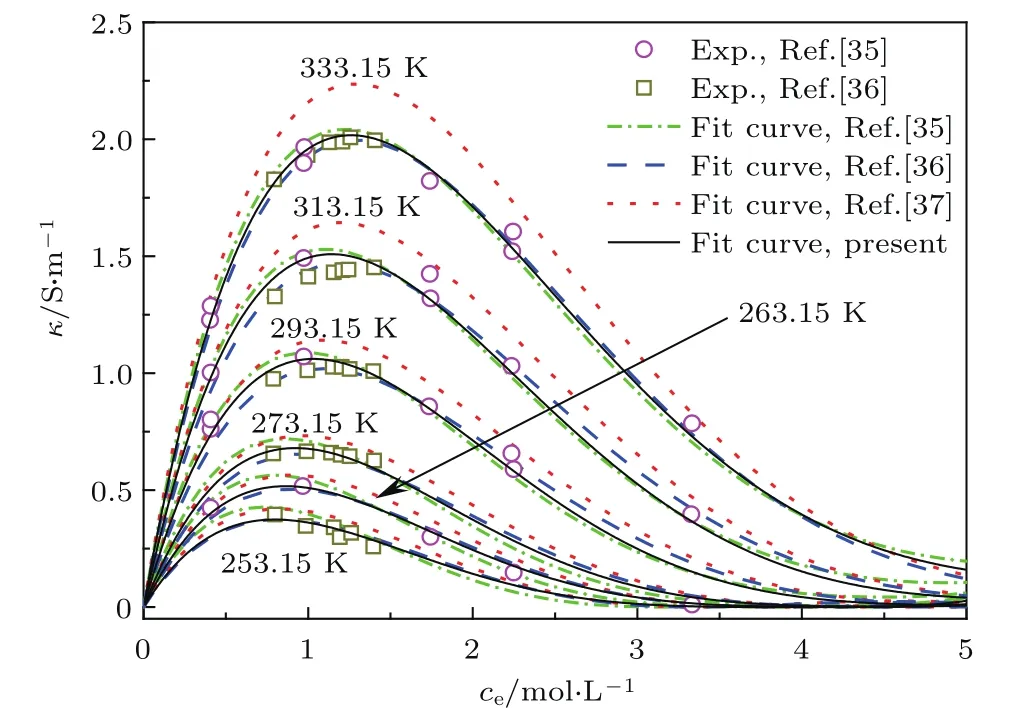
图4 电解液中Li+传导系数随温度和Li+浓度的变化Fig.4.Ionic conductivity of the liquid electrolytic solution as a function of salt concentration and temperature.
2.3 模型求解
在给定边界和初始条件的情况下,表1中的控制方程可借助基于有限元方法的商业软件——COMSOL MULTIPHYSICS®(5.3版)求解出充放电过程中电池内各电化学参量(如ϕs,ϕe,cs,ce和T)的动态分布信息;同时,还可获得充放电过程中电池内各产热量(如qec,qre,qeo,qio和qim)的动态分布信息以及电池放电曲线、表面温升曲线、最大放电容量和平均输出功率等信息.由模型假设4可知,放电曲线可近似为任意时刻(或任意放电量),正极集流体和膜片之间交界面上的平均电压与负极集流体和膜片之间交界面上的平均电压之差:
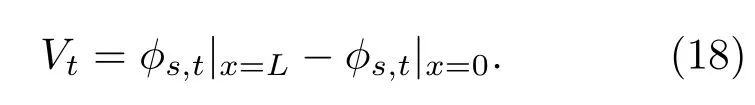
表面温升曲线则可近似为任意时刻(或任意放电量),电池正极集流体和膜片交界面上平均温度的变化曲线.
3 模型验证
运用第2节模型模拟容量为11.8 Ah的LiMn2O4|LiPF6|LiC6电池在环境温度为300.15 K时的放电过程.模型模拟时除了需要输入开路势(图2)和熵系数(图3)之外,还需要输入电池几何结构参数、隔膜/电极膜片孔隙结构参数、制备电池所用材料的物性参数以及电池内各电化学参量的初始值等,如表2所列.

表2 模拟所用参数Table 2.Parameters used in the simulations.
图5给出了不同放电倍率下LiMn2O4|LiPF6|LiC6电池放电曲线和表面温升曲线.从图5(a)中可看出:不管采用0.2 C,0.5 C,1.0 C还是2.0 C放电,电池输出电压随着放电时间的增加均呈不断下降的趋势;在放电时间相同的情况下,电池输出电压随放电倍率的升高呈不断减小的趋势;当截止电压均为2.6 V(下文未特别指明,截止电压均为该值)时,电池可放电时间随放电倍率的增大而减小.从图5(b)中可看出:放电倍率不同,电池表面温升曲线的变化趋势也不相同,例如采用0.2 C放电时,电池表面温度呈先升高后降低最后再升高的变化趋势,放电结束时电池表面温度为28.5◦C,仅比环境温度高1.5◦C;而采用2.0 C放电时,电池表面温度始终呈不断升高的变化趋势,放电结束时电池表面温度高达57.7◦C,比环境温度高30.7◦C.结合图5(a)和图5(b)可知:本文模型计算结果较文献[23]中的模型计算结果更加接近实验测试数据,这表明本文模型计算结果的准确性更高.
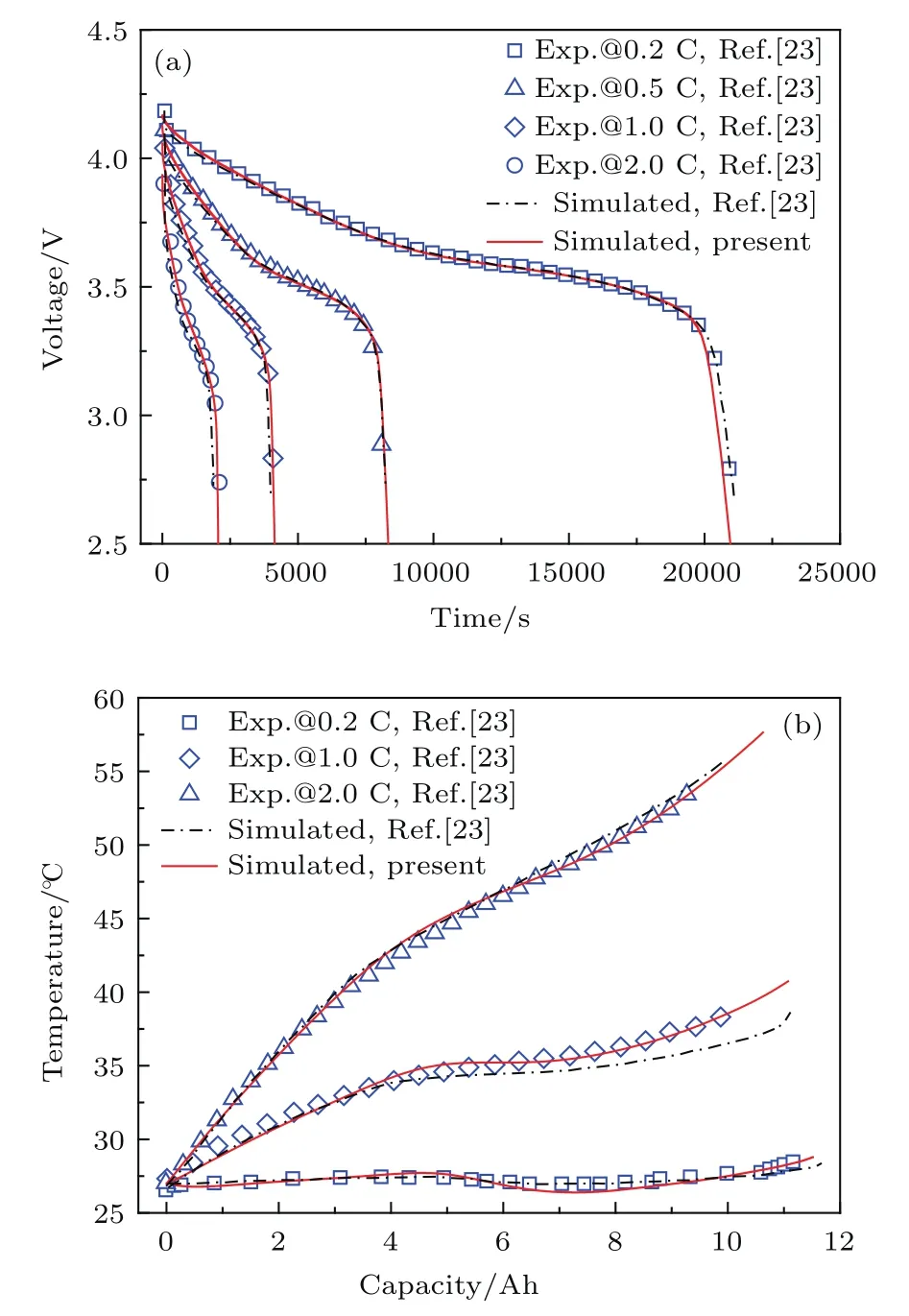
图5 模型计算结果与文献[23]中的实验测试和模型计算结果的对比 (a)电池放电曲线;(b)电池表面温升曲线Fig.5.Comparison of simulated results by the present model with experimental data and simulated results from Ref.[23]:(a)Battery discharge curve;(b)battery surface temperature rise curve.
4 结果分析
孔隙率和扭曲率是隔膜的两个重要孔隙结构参数.为此,本文利用经实验测试数据和文献[23]中模型计算结果验证后的电化学-热耦合模型深入分析上述参数对锂离子电池性能的影响规律.
4.1 孔隙率的影响
为了明确隔膜孔隙率对锂离子电池性能的影响规律,本文对采用具有不同孔隙率的隔膜(隔膜扭曲率为1.69,其他参数的取值如表2所列)制备而成的锂离子电池在不同倍率下的放电过程进行了仿真分析,图6—图8分别给出了隔膜孔隙率对锂离子电池放电曲线、表面温升曲线、最大放电容量和平均输出功率的影响,其中最大放电容量为电池从额定容量放电至截止电压时所放出的电量;平均输出功率为电池从额定容量放电至截止电压时输出功率的平均值,计算公式如下:
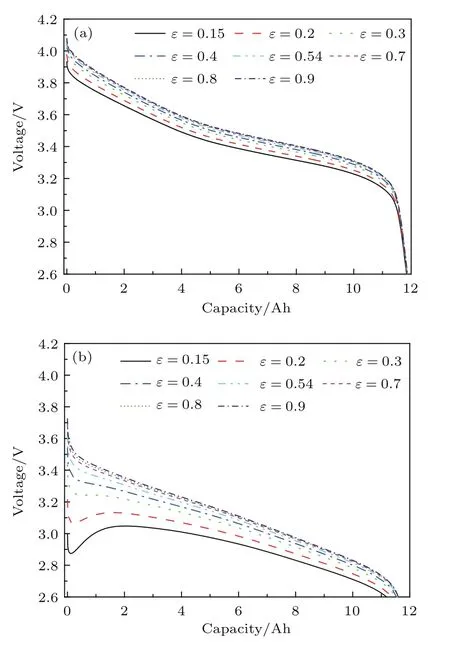
图6 隔膜孔隙率对锂离子电池放电曲线的影响 (a)1 C;(b)5 CFig.6. Effect of separator porosity on the discharge curve of the lithium-ion battery:(a)1 C;(b)5 C.

式中Γ为整数,∆t为时间步长.
从图6中可看出:不管采用1 C还是5 C放电,随着隔膜孔隙率不断减小,电池放电曲线的电压平台均在不断下降;在5 C放电时,当隔膜孔隙率减小到一定程度,放电初期电池输出电压会出现先降低后回升的现象,且隔膜孔隙率越小,放电初期电池输出电压下降的幅度越大、速度越快,回升所需时间也越长.例如当隔膜孔隙率为0.15时,电池仅放出0.13 Ah的电量其输出电压就下降至最低电压点(2.87 V),而回升至最高电压点(3.05 V)时电池放电量已达到2.04 Ah;另外,当隔膜孔隙率相同时,电池放电曲线的电压平台随放电倍率的增大而降低.
从图7中可看出:除初始放电时刻之外,不管电池采用1 C还是5 C放电,在放电量相同的情况下电池表面温度和温升速度均随隔膜孔隙率的减小而增大;放电倍率不同,电池表面温升曲线随放电量增大呈现出不同的变化趋势,即采用1 C放电时电池表面温升曲线随放电量增大呈先升高后趋于平稳最后再升高的变化趋势,而采用5 C放电时电池表面温升曲线随放电量的增大始终呈不断升高的趋势;另外,除初始状态之外,在隔膜孔隙率和放电量均相同时,电池表面温度和温升速度均随放电倍率的增大而升高.

图7 隔膜孔隙率对锂离子电池表面温升曲线的影响 (a)1 C;(b)5 CFig.7.Effect of separator porosity on the surface temperature rise curve of the lithium-ion battery:(a)1 C;(b)5 C.
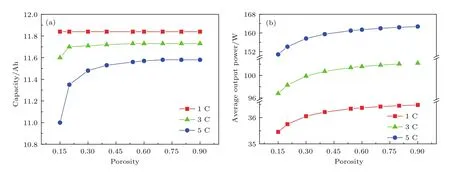
图8 隔膜孔隙率对锂离子电池性能的影响 (a)最大放电容量(b)平均输出功率Fig.8.Effect of separator porosity on the performance of the lithium-ion battery:(a)Maximum discharge capacity;(b)average output power.
从图8中可看出:无论采用1 C,3 C还是5 C放电,锂离子电池最大放电容量和平均输出功率随隔膜孔隙率的增大均呈先升高后趋于恒定的变化趋势.放电倍率越小,隔膜孔隙率对锂离子电池最大放电容量和平均输出功率的影响越小,反之则越大.例如,隔膜孔隙率由0.15增至0.90的过程中,若采用1 C放电,电池最大放电容量由11.836 Ah逐渐增大并最终恒定在11.844 Ah,平均输出功率由35.45 W 逐渐增大并最终恒定在36.48 W,最大放电容量和平均输出功率分别增大了0.07%和2.91%;而采用5 C放电时电池最大放电容量和平均输出功率分别增大了5.17%和7.90%.另外,当隔膜孔隙率相同时,随着放电倍率不断增大,电池最大放电容量不断减小、平均输出功率不断增大,例如当隔膜孔隙率为0.15时,电池采用1 C,3 C和5 C放电时,其最大放电容量分别为11.836,11.6和11.0 Ah,平均输出功率分别为35.45,96.79和150.83 W.
4.2 扭曲率的影响
为了明确隔膜扭曲率对锂离子电池性能的影响规律,本文对采用具有不同扭曲率的隔膜(隔膜孔隙率为0.54,其他参数的取值如表2所列)制备而成的锂离子电池在不同倍率下的放电过程进行了仿真分析,图9—图12分别给出了隔膜扭曲率对电池放电曲线、表面温升曲线、最大放电容量和平均输出功率的影响.从图9中可看出:不管电池采用1 C还是5 C放电,随着隔膜扭曲率不断增大,电池放电曲线的电压平台均在不断降低;当隔膜扭曲率增大到一定程度时,放电初期电池输出电压均会出现先下降后回升的现象,且隔膜扭曲率越大,其下降的幅度更大、速度更快,极有可能导致其低于截止电压,若其下降至最低点时刚好等于截止电压,则将制备此电池所用隔膜的扭曲率定义为隔膜临界扭曲率.例如,隔膜孔隙率为0.54的电池,采用1 C放电时隔膜临界扭曲率为9.3,如图9(a)所示;采用5 C放电时隔膜临界扭曲率为3.7,如图9(b)所示.可见,隔膜临界扭曲率与放电倍率密切相关.另外,当隔膜扭曲率相同时,采用较大倍率放电时电池放电曲线的电压平台较低.

图10 隔膜扭曲率对锂离子电池表面温升曲线的影响 (a)1 C;(b)5 CFig.10.Effect of separator tortuosity on the surface temperature rise curve of the lithium-ion battery:(a)1 C;(b)5 C.
从图10中可看出:除初始放电时刻之外,不管电池采用1 C还是5 C放电,在放电量相同的情况下电池表面温度和温升速度均随隔膜扭曲率的增大而增大;放电倍率不同,电池表面温升曲线随放电容量的不断增大呈现出不同的变化趋势,例如采用1 C放电时电池表面温升曲线随放电量的不断增大呈先升高后趋于平稳最后再升高的变化趋势,而采用5 C放电时电池表面温升曲线随放电量的不断增大始终呈不断升高的趋势;另外,除初始状态之外,当隔膜扭曲率和放电量均相同时,电池表面温度和温升速度均随放电倍率的增大而升高.
结合图11和图12可以看出:不管采用1 C还是5 C放电,在隔膜孔隙率相同的情况下,电池最大放电容量和平均输出功率均随隔膜扭曲率的增大而减小,在隔膜扭曲率相同的情况下电池最大放电容量和平均输出功率均随隔膜孔隙率的增大而增大.另外,在隔膜孔隙率和扭曲率相同的情况下,随着放电倍率的不断增大,电池最大放电容量不断减小,平均输出功率却不断升高.然而,在如图11和图12中给定的隔膜孔隙率和扭曲率变化范围内,当电池采用较小的倍率放电时,相对于电池最大放电容量的降幅,电池平均输出功率的降幅相对较大.例如,采用1 C放电时,电池最大放电容量介于11.33和11.846 Ah之间,相对于最大的电池最大放电容量,最小的电池最大放电容量下降了4.36%,如图11(a)所示;电池平均输出功率介于29.54和36.86 W之间,相对于最大的电池平均输出功率,最小的电池平均输出功率下降了19.86%,如图12(a)所示.另外,随着放电倍率不断增大,电池最大放电容量的降幅逐渐增大,电池平均输出功率的降幅逐渐降低.例如,采用5 C放电时,电池最大放电容量介于10.75和11.6 Ah之间,相对于最大的电池最大放电容量,最小的电池最大放电容量下降了7.33%,如图11(b)所示;电池平均输出功率介于146.49和164.84 W之间,相对于最大的电池平均输出功率,最小的电池平均输出功率下降了11.13%,如图12(b)所示.
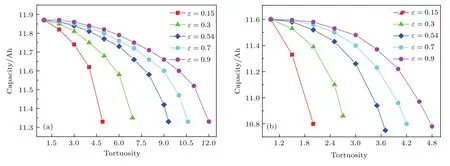
图11 隔膜扭曲率对锂离子电池最大放电容量的影响 (a)1 C;(b)5 CFig.11.Effect of separator tortuosity on the maximum discharge capacity of the lithium-ion battery:(a)1 C;(b)5 C.
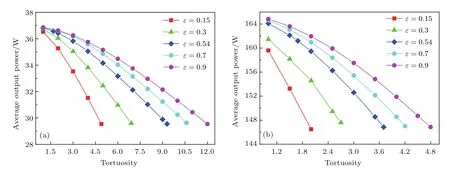
图12 隔膜扭曲率对锂离子电池平均输出功率的影响 (a)1 C;(b)5 CFig.12.Effect of separator tortuosity on the average output power of the lithium-ion battery:(a)1 C;(b)5 C.
此外,结合图11和图12还可发现,隔膜临界扭曲率除了与放电倍率相关之外,还与隔膜孔隙率密切相关.为此,本文提取了隔膜临界扭曲率与隔膜孔隙率和放电倍率之间的关联关系,并绘制在图13中.从图13中可看出:隔膜临界扭曲率随隔膜孔隙率的增大呈近似线性增大的关系,且斜率随放电倍率的增大而减小,这表明要确保电池倍率性和放电初期电池输出电压不低于截止电压,隔膜扭曲率取值范围随隔膜孔隙率的增大而增大;在隔膜孔隙率相同的条件下,隔膜临界扭曲率随放电倍率的增大而减小,这表明要确保放电初期电池输出电压不低于截止电压,隔膜扭曲率取值范围随放电倍率的增大而减小.

图13 隔膜临界扭曲率与隔膜孔隙率和放电倍率之间的关联关系Fig.13.The relationship of the separator critical tortuosity,separator porosity and discharge rate.
5 讨 论
根据(15)式可知:在隔膜扭曲率(如τ=1.69)保持不变的情况下,隔膜有效Li+扩散(传导)系数均随隔膜孔隙率的减小而减小,这表明隔膜传输Li+的阻力随隔膜孔隙率的减小而增大.这一方面会造成电池放电曲线的电压平台随隔膜孔隙率减小而降低,如图6所示,同时也会造成电池平均输出功率随隔膜孔隙率减小而降低,如图8(b)所示;另一方面还会造成电池内部qio和qim随隔膜孔隙率减小而升高,如图14(d)和图14(e)所示.此外,图14中还给出了隔膜孔隙率对5 C放电过程中电池内部qec,qre,qeo和q的影响,从图中可看出:qre和qeo几乎不受隔膜孔隙率的影响,如图14(b)和图14(c)所示.qec随隔膜孔隙率升高呈先升高后趋于恒定的变化趋势,如图14(a)所示,主要原因是当隔膜孔隙率较小时,隔膜内部电解液中Li+传输阻力较大,极有可能造成负极膜片内部电化学反应生成的Li+堆积在活性位附近,正极膜片内部电解液中Li+来不及输送至电化学反应活性位,从而引发局部电化学反应无法进行或反应速度较小等现象;当隔膜孔隙率增大到一定程度时,不再会出现因为隔膜内部Li+输运不及时而影响电化学反应的发生或速度[40].对图14(a)—(e)中的qec,qre,qeo,qio和qim进行累加,可得到如图14(f)所示的q.从图中可看出:q随隔膜孔隙率的减小而不断升高,这表明电池内部(包括表面)温度和温升速度随隔膜孔隙率的减小而升高,如图7所示.
根据(15)式可知:在隔膜孔隙率(如ε=0.54)保持不变的情况下,隔膜有效Li+扩散(传导)系数均随隔膜扭曲率的增大而减小,这表明隔膜传输Li+的阻力随隔膜扭曲率的增大而增大.这一方面会造成电池放电曲线的电压平台随隔膜扭曲率的增大而降低,如图9所示,同时也会造成电池平均输出功率随隔膜扭曲率的增大而降低,如图12所示;另一方面,还会造成电池内部qio和qim随隔膜扭曲率的增大而升高,如图15(d)和图15(e)所示.此外,图15中还给出了隔膜扭曲率对5 C放电过程中电池内部qec,qre,qeo和q的影响.从图中可看出:qre和qeo几乎不受隔膜扭曲率的影响,如图15(b)和图15(c)所示;qec随隔膜扭曲率的增大而增大,如图15(a)所示.主要原因是当隔膜扭曲率较大时,隔膜内部Li+传输阻力也较大,极有可能造成负极膜片内部电化学反应生成的Li+堆积在活性位附近,正极膜片内部电解液中Li+来不及输送至电化学反应活性位,从而引发电化学反应无法进行或反应速率较小等现象[40].对图15(a)—(e)中的qec,qre,qeo,qio和qim进行累加,可得到如图15(f)所示的q.可以看出:q随隔膜扭曲率的增大而增大,这表明电池内部(包括表面)温度和温升速度随隔膜扭曲率的增大而增大,见图10.
综合图14和图15可知:在放电末期q的变化趋势主要取决于qec,而其他放电时刻则主要取决于qio;另外,随着隔膜孔隙率降低或扭曲率升高,放电过程中q将由先快速升高后缓慢升高的变化趋势转变成先快速升高后缓慢降低再缓慢升高的变化趋势.这表明随着隔膜孔隙率降低或扭曲率升高,放电过程中电池内阻(电子欧姆、离子欧姆、电化学极化和浓差极化等内阻之和)也将由先快速升高后缓慢升高的变化趋势转变成先快速升高后缓慢下降再缓慢升高的变化趋势,进而造成电池输出电压由先快速下降后缓慢下降的变化趋势转变成先快速下降后缓慢升高再缓慢下降的变化趋势,如图6和图9所示.产生上述现象的主要原因是隔膜有效Li+扩散(传导)系数除了与其孔隙率、扭曲率等孔隙结构参数相关之外,还与电解液中Li+浓度和温度密切相关,如(15)和(16)式以及图4所示.以孔隙率和扭曲率分别为0.54和3.7的隔膜制备而成的锂离子电池为例,采用5 C放电时,尽管电池内部(包括表面)温度和温升速度始终呈不断升高的变化趋势,但电解液中Li+浓度随时间和空间的变化趋势均在不断改变,如图10(b)和图16所示,因此电解液中Li+浓度和温度在不同时刻、不同位置对隔膜有效Li+扩散(传导)系数的贡献也不尽相同.
1)在放电初期,电解液温度升高(如图10(b)所示)和正极膜片内部电解液中Li+浓度降低(如图16所示)均会造成电解液中Li+传导系数不断升高(如图4所示),但与负极膜片内部电解液中Li+浓度升高(如图16所示)造成电解液中Li+传导系数不断减小(如图4所示)相比还无法抵消,因而电池内阻不断增大、输出电压不断降低(如图9(b)所示).
2)在放电初期电池输出电压下降至最低点之后:电解液温度继续升高(如图10(b)所示)、正极膜片内部电解液中Li+浓度升高(如图16所示)和负极膜片内部电解液中Li+浓度降低(如图16所示)均会造成电解液中Li+传导系数不断增大(如图4所示),因而电池内阻不断减小、输出电压不断升高(见图9(b)).
3)在放电中期q下降至最低点之后:电解液温度仍不断升高(如图10(b)所示)会造成电解液中Li+传导系数不断升高(如图4所示),但与正极膜片内部电解液中Li+浓度降低(如图16所示)和负极膜片内部电解液中Li+升高(如图16所示)造成电解液中Li+传导系数不断减小(如图4所示)相比还无法抵消,因而电池内阻不断升高、输出电压不断降低(如图9(b)所示).
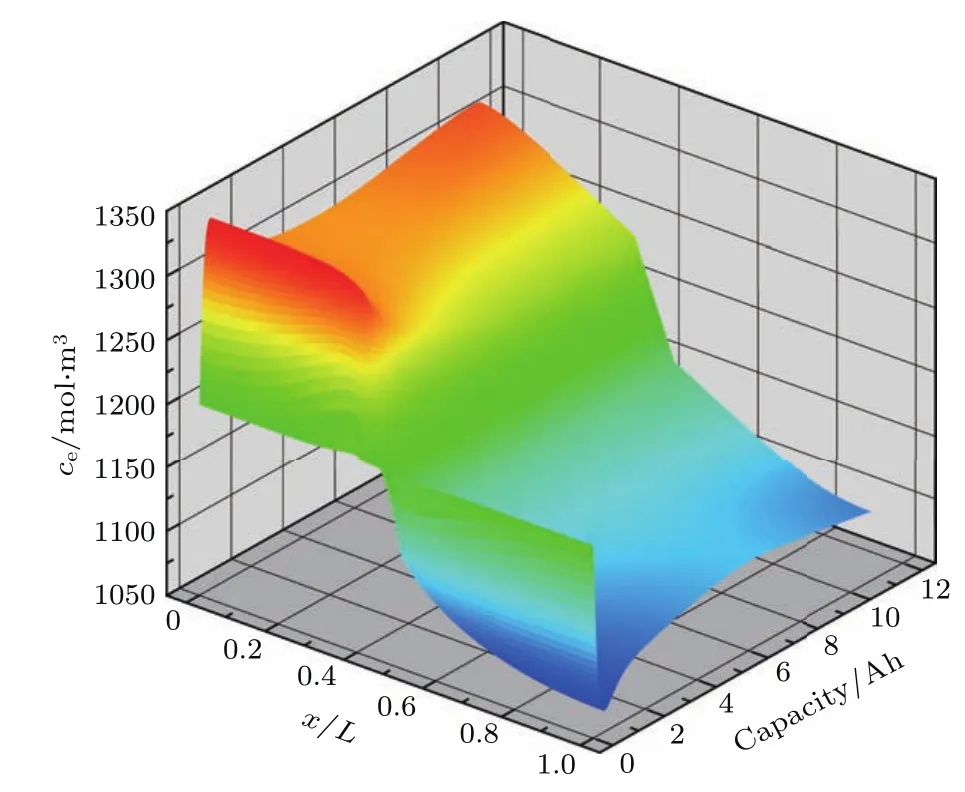
图16 孔隙率和扭曲率分别为0.54和3.7的隔膜制备而成的锂离子电池在5 C放电过程中电解液内Li+浓度的时空变化图Fig.16.Spatial and temporal distribution of the Li+concentration in electrolyte for lithium-ion battery with the separator porosity equaled to 0.54 and tortuosity equaled to 3.7 during 5 C discharge process.
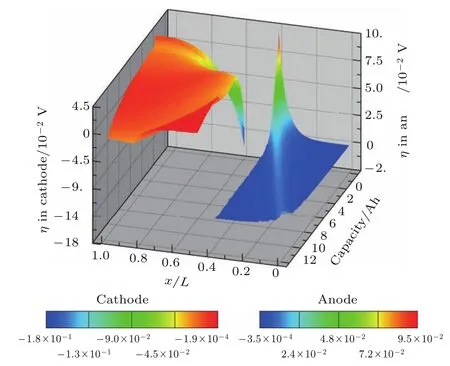
图17 孔隙率和扭曲率分别为0.54和3.7的隔膜制备而成的锂离子电池在5 C放电过程中电极膜片内过电势的时空变化图Fig.17.Spatial and temporal distribution of the overpotential in electrodes for lithium-ion battery with the separator porosity equaled to 0.54 and tortuosity equaled to 3.7 during 5 C discharge process.
4)在放电末期:一方面,电解液温度还在不断升高(如图10(b)所示)会造成电解液中Li+传导系数不断升高(如图4所示),但与正极膜片内部电解液中Li+浓度不断降低(如图16所示)和负极膜片内部电解液中Li+浓度不断升高(如图16所示)造成电解液中Li+传导系数不断减小(如图4所示)相比还无法抵消,因而qio会不断下降(如图15(d)所示);另一方面,正、负极膜片内部过电势、传输流密度的绝对值在放电末期均稍有增大,如图17和图18所示,因而qec会不断升高(如图15(a)所示).
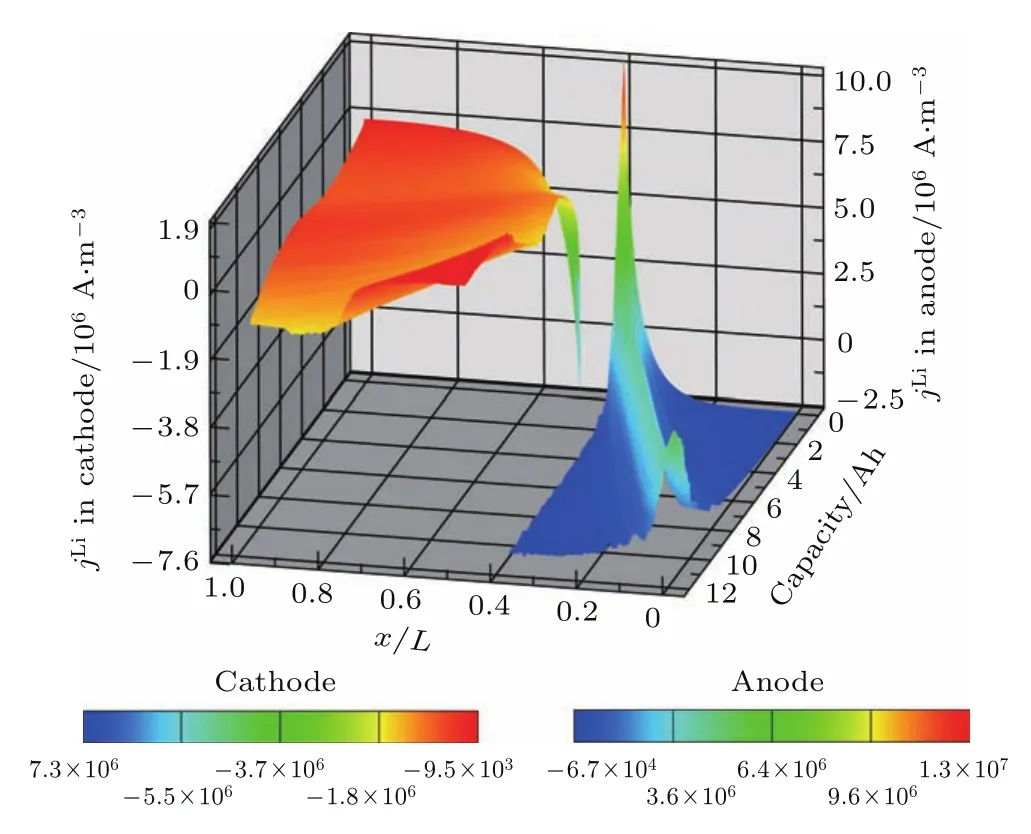
图18 孔隙率和扭曲率分别为0.54和3.7的隔膜制备而成的锂离子电池在5 C放电过程中电极膜片内传输流密度的时空变化图Fig.18.Spatial and temporal distribution of the transfer current density in electrodes for lithium-ion battery with the separator porosity equaled to 0.54 and tortuosity equaled to 3.7 during 5 C discharge process.
6 结 论
本文借助COMSOL MULTIPHYSICS软件平台开发了锂离子电池电化学-热耦合模型,并利用其分别揭示隔膜孔隙率和扭曲率对锂离子电池性能的影响机制,得出如下结论.
1)相比文献[23]中模型的计算结果,本文所开发的锂离子电池电化学-热耦合模型计算的放电曲线和表面温升曲线更加接近实验测试数据.
2)减小隔膜孔隙率或增大隔膜扭曲率,电池放电曲线的电压平台、最大放电容量和平均输出功率均不断降低,电池表面温度和温升速度均不断升高;当孔隙率减小或扭曲率增大到一定程度时,放电初期电池输出电压均会出现先下降后回升的现象,且孔隙率越小或扭曲率越大,其下降的幅度越大、速度越快,回升所需时间也越长.
3)在本文给定的隔膜孔隙率和扭曲率变化范围内,当电池采用较小的倍率放电时,相对于最大放电容量的降幅,平均输出功率的降幅相对较大.随着放电倍率不断增大,最大放电容量的降幅逐渐增大,平均输出功率的降幅逐渐降低.
4)隔膜临界扭曲率随隔膜孔隙率的增大呈近似线性增大的关系,且斜率随放电倍率的增大而减小;在隔膜孔隙率相同的情况下,隔膜临界扭曲率随放电倍率的增大而减小.
5)隔膜孔隙率和扭曲率等孔隙结构参数主要影响电池放电末期正、负极膜片内部电化学反应以及其他放电时刻电解液中有效Li+扩散(传导)系数.
综上可知,在隔膜孔隙结构的设计与优化过程中,除了需要确保隔膜具备良好的化学稳定性、热稳定性、空间结构稳定与平整性以及足够的机械强度(穿刺和拉伸强度)之外,还必须权衡以其制备的锂离子电池输出电压、容量和功率(倍率)以及锂离子电池内部(包括表面)温度和温升速度(热安全)等特性.可见,本文所取得的研究成果不仅可为隔膜孔隙结构的设计与优化提供理论指导和技术支持,而且还对促进隔膜制备工艺的改进和完善具有重要的现实意义.
