具有感觉记忆的忆阻器模型
2019-01-25邵楠张盛兵邵舒渊
邵楠 张盛兵 邵舒渊
1)(西北工业大学计算机学院,西安 710072)
2)(西北工业大学电子信息学院,西安 710072)
(2018年8月22日收到;2018年11月15日收到修改稿)
人类记忆的形成包括感觉记忆、短期记忆、长期记忆三个阶段,类似的记忆形成过程在不同材料忆阻器的实验研究中有过多次报道.这类忆阻器的记忆形成过程存在有、无感觉记忆的两种情况,已报道的这类忆阻器的数学模型仅能够描述无感觉记忆的忆阻器.本文在已有模型的基础上,根据有感觉记忆的忆阻器的研究文献中所报道的实验现象,设计了具有感觉记忆的忆阻器模型.对所设计模型的仿真分析验证了该模型对于存在感觉记忆的这类忆阻器特性的描述能力:对忆阻器施加连续脉冲激励,在初始若干脉冲作用时忆阻器无明显的记忆形成,此时忆阻器处于感觉记忆阶段,后续的脉冲作用下忆阻器将逐渐形成短期、长期记忆,并且所施加脉冲的幅值越大、宽度越大、间隔越小,则感觉记忆阶段所经历的脉冲数量越少.模型状态变量的物理意义可用连通两电极的导电通道在外加电压作用下的形成与消失来给出解释.
1 引 言
在Atkinson-Shiffrin记忆模型[1]中,人类记忆的形成过程包括感觉记忆(sensory memory,SM)、短期记忆(short-term memory,STM)和长期记忆(long-term memory,LTM)三个阶段:人们对于所接收到的来自周围环境的各种信号会产生感觉记忆,当意识关注于某个信号时便会对于这个信号形成短期记忆,若这个信号不再出现,则相应的短期记忆会较快被遗忘,若这个信号仍然反复多次出现并且被关注,那么相应的短期记忆将逐渐变为长期记忆,长期记忆能够持续存在较长时间.图1给出了Atkinson-Shiffrin记忆模型所描述的记忆形成过程.
在多篇关于不同材料忆阻器的实验研究中,类似Atkinson-Shiffrin记忆模型所描述的记忆与学习过程的实验现象被多次报道[2-19].这些研究中,通常将忆阻器阻值的变化看作是忆阻器记忆的形成和遗忘:阻值减小则记忆逐渐形成,阻值增大则记忆逐渐遗忘.在外加电压作用下,这类忆阻器会形成类似人类记忆的短期记忆和长期记忆,并且施加更多的电压激励可使得更多的短期记忆逐渐变为长期记忆.

图1 Atkinson-Shiffrin记忆模型Fig.1.Atkinson-Shiffrin memory model.
文献所报道的这些实验现象中,不同材料的忆阻器从高阻状态开始,在连续脉冲激励初始阶段的电阻变化过程并不完全相同:有的忆阻器[2-16]在初始脉冲激励作用下电阻就开始减小;还有的忆阻器[17-19]在初始的若干脉冲激励作用时,电阻无明显变化,之后的脉冲激励作用下电阻才开始逐渐减小.前一类忆阻器在脉冲激励初始阶段记忆就开始形成,连续脉冲激励作用下将逐渐形成短期记忆以及长期记忆,将这类忆阻器称为“STM→LTM忆阻器”;后一类忆阻器在脉冲激励初始阶段的忆阻记忆特点与Atkinson-Shiffrin记忆模型中的感觉记忆相似,之后的连续脉冲作用下才开始逐渐形成短期记忆以及长期记忆,将这类忆阻器记称为“SM→STM→LTM忆阻器”.
忆阻器的数学模型是忆阻器理论研究和应用设计的基础.文献[20—25]对于这类忆阻器的数学模型进行了讨论:文献[20]在文献[26]中所提出的具有遗忘特性的忆阻模型的基础上,对该模型的遗忘项进行了改进,提出了STM→LTM忆阻器的数学模型;文献[21—24]对文献[20]所提出的忆阻模型做了进一步的讨论;文献[25]在对上述模型的分析中发现,多次报道的这类忆阻器的实验研究中的一些实验现象,该模型无法描述,并提出新的数学模型,该模型能够更全面地描述这类忆阻器已报道的实验现象.上述已报道的忆阻模型研究均是针对STM→LTM忆阻器,尚未见对SM→STM→LTM忆阻器数学模型的讨论.
本文对于SM→STM→LTM忆阻器的数学模型进行了讨论. 本文首先对文献[25]中的STM→LTM忆阻模型给出介绍,然后在该模型基础上,根据对SM→STM→LTM忆阻器感觉记忆阶段的特点的分析,设计SM→STM→LTM忆阻器模型,最后对所设计的模型描述SM→STM→LTM忆阻器特性的能力进行仿真验证,并讨论了模型中各个状态变量的物理意义.
2 STM→LTM忆阻模型
文献[25]中所提出的STM→LTM忆阻器的数学模型如下:
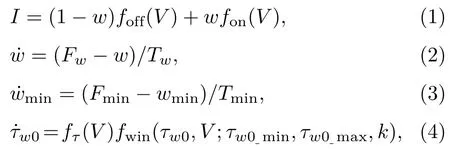
其中(1)式为基于状态的伏安关系方程,I为流过忆阻器的电流,V为忆阻器两端的电压,foff(·)和fon(·)分别描述了忆阻器高阻状态和低阻状态的伏安特性,状态变量w∈[0,1]决定这两项的权重.w的变化描述了忆阻器记忆的形成与遗忘,状态方程(2)给出了在输入电压V作用下w随时间t的变化规律,其中,Fw∈[0,1]描述了w在不同电压作用时的变化方向,根据已报道的相关实验现象,Fw随电压V的变化应为形如“”的曲线,该曲线的快速上升发生在某一正电压附近.文献[25]中所设计的Fw为

其中,0 6wmin6w6wmax=1,wmin描述了忆阻器长期记忆,fu(V)定义如下
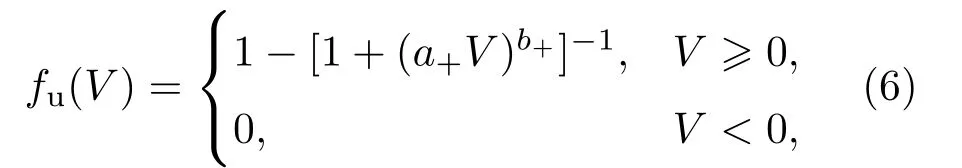
式中a+和b+均为正常数,Fw在V=1/a+附近将快速上升,b+决定了这个上升过程的快慢,Fw关于V的曲线如图2(a)所示;Tw>0描述了w在不同电压作用时变化的快慢,根据已报道的相关实验现象,Tw随电压V的变化应为形如“_⊓_”的曲线,快速上升和下降应分别发生在某一负电压和某一正电压附近,文献[25]中所设计的Tw为

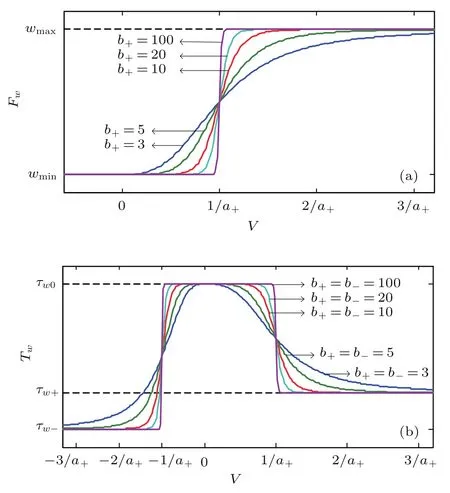
图2 Fw和Tw关于输入电压V的曲线 (a)Fw;(b)TwFig.2.Curves of(a)Fwand(b)Twwith respect to V.
其中0<τw-6τw+6τw0;a-,b-,τw+,τw-均为正常数,τw0描述了忆阻器遗忘曲线的时间常数.Tw随电压V的变化而上升和下降分别发生在V=-1/a-和V=1/a+附近,上升和下降的变化快慢分别由b-和b+的大小决定;Tw关于V的曲线如图2(b)所示.长期记忆wmin在外加电压作用下的变化规律与w相似,状态方程(3)给出了wmin的变化规律,其中Fmin=fF(V,0,w),Tmin=fT(V,τmin0,τmin+,τmin-),τmin0,τmin+,τmin-均为常数,且0<τmin-6τmin+6τmin0. 状态方程(4)给出了遗忘曲线的时间常数τw0在外加电压作用下的变化规律,其中
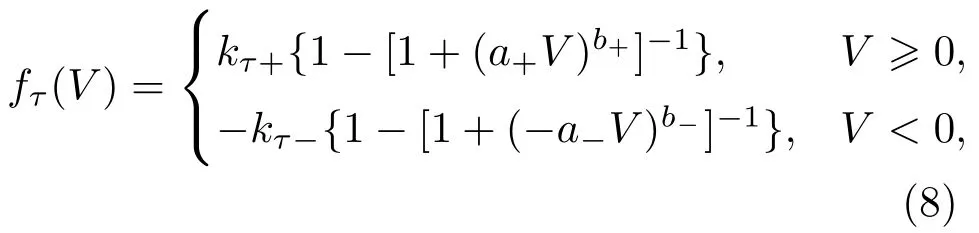
kτ+和kτ-均为正常数,函数fτ(V)曲线如图3所示,作用电压V>1/a+时τw0会明显递增,V<-1/a-时τw0会明显递减,窗口函数fwin(·)用以限定τw0的变化范围,

其中,0<τw0_min6τw06τw0_max, 函数fs(·)定义为


图3 函数fτ(V)的曲线Fig.3.Curve of fτ(V).
已报道的相关研究中,遗忘曲线时间常数在脉冲激励作用下的变化存在有、无上限两种情况,k取值为0或1,它决定τw0的上限是否存在:若k=1,τw0存在上限τw0_max, 此时τw0_min6τw06τw0_max; 若k=0,τw0无上限, 此时τw0>τw0_min.
在这类忆阻器的实验中,遗忘过程的阻变情况是通过观察在较小的常值正电压作用下流过忆阻器的电流的变化而得到的.在上述模型中,这个较小的正电压Vlow+定义为
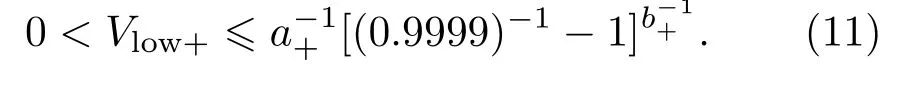
模型状态变量w,wmin,τw0在作用电压为Vlow+时的变化与作用电压为0 V时的变化情况几乎一致.
3 SM→STM→LTM忆阻模型
SM→STM→LTM忆阻器在连续脉冲作用下形成短期记忆和长期记忆之前,还存在感觉记忆阶段.在该阶段,作用在忆阻器上的脉冲激励不会引起忆阻器阻值的明显变化,即在感觉记忆阶段没有明显的记忆形成;所施加脉冲的幅值越大、宽度越大、间隔越小,则感觉记忆阶段所经历的脉冲数量越少[17-19].
在第2节所介绍的STM→LTM忆阻器模型中,由状态方程(2)可知,状态变量w在外加电压作用下将逐渐趋向于Fw,Tw决定了这个变化的快慢,由图2给出Fw,Tw随输入电压V的变化曲线可以看出,Fw和Tw的大小均是在V=1/a+附近发生明显的改变,即a+决定了在正电压作用时w发生明显递增的电压大小;对状态方程(3)和(4)的分析可知,a+也同样决定了wmin和τw0发生明显递增时所施加正电压的大小.
将原模型中的常数a+重新定义为状态变量,即可得到具有“感觉记忆”的SM→STM→LTM忆阻器模型:初始时刻忆阻器处于高阻状态,a+较小,作用在忆阻器上的脉冲幅值明显小于1/a+,此时的脉冲作用下w,wmin,τw0均无明显变化,忆阻器处于感觉记忆阶段;连续的脉冲激励作用会使得a+逐渐增大,脉冲幅值将逐渐大于1/a+,此时的脉冲作用会逐渐使得w,wmin,τw0有明显的增长,忆阻器的短期记忆和长期记忆将逐渐形成.
在已报道的这类忆阻器的实验研究中,较小的正电压作用下始终不会有明显的记忆形成(即w不会增长),因此1/a+应有下限(即a+存在上限);若脉冲幅值足够大,初始脉冲作用时就可观察到有记忆形成(即w在初始脉冲作用下就开始增长),因此1/a+有上限(即a+存在下限);负电压作用时这类忆阻器的阻值的变化情况在已有的实验研究中报道较少,模型中的状态变量w,wmin,τw0在负电压作用时均是向其下限方向变化,这里我们假设a+在负电压作用时也向其下限方向递减.由以上分析可看出,a+在外加电压作用下的变化规律与τw0相似,因此a+的状态方程设计为
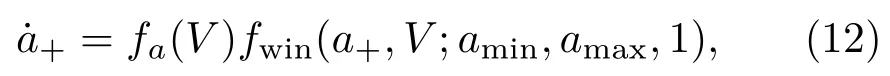
其中,窗口函数fwin(·)保证了a+的变化始终在[amin,amax]以内,因为a+存在上限amax,故在这里的窗口函数中k=1;fa(V)描述了在不同电压作用下a+的变化,
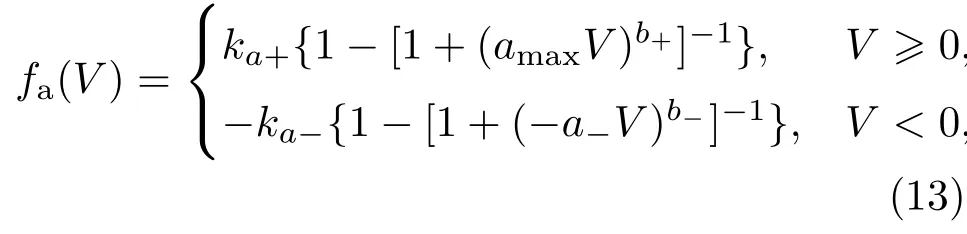
ka+,ka-为正常数.图4给出了函数fa(V)的曲线,fa(V)与(8)式所给出的fτ(V)形式相似,两函数除了系数ka+,ka-与kτ+,kτ-的不同,V>0时两函数发生明显递增的位置也不相同:fa(V)随电压V的变化曲线在V=1/amax附近快速上升,1/amax为常数,而fτ(V)在V=1/a+附近快速上升,a+的变化会使得fτ(V)发生明显递增时V的取值发生相应的改变.
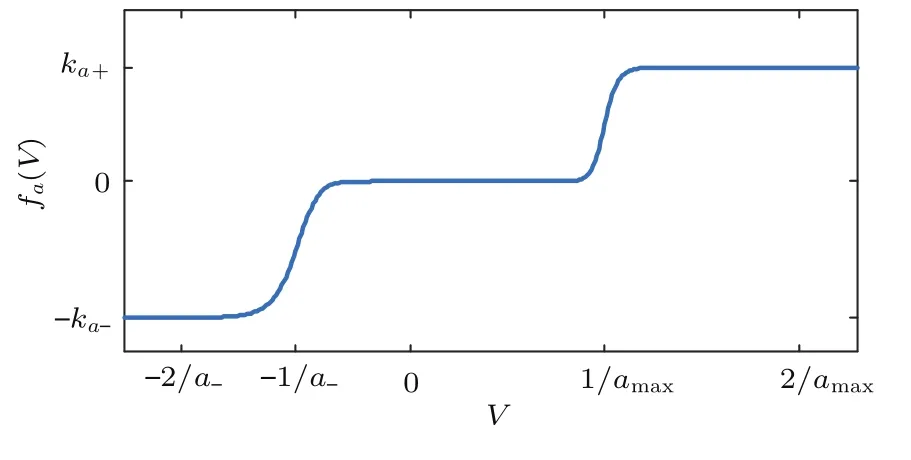
图4 函数fa(V)的曲线Fig.4.Curve of fa(V).
由于这里所设计的SM→STM→LTM忆阻模型将原STM→LTM忆阻模型中的常数a+重新定义为变量,因此,在遗忘过程中用以观察阻值变化的较小正电压Vlow+若仍然使用原定义,则其上限将受作用电压的影响而发生变化.将Vlow+重新定义为

这里将原定义的上限中的1/a+改为1/amax,以保证其上限为定值.
4 仿 真
前文在已有的STM→LTM忆阻器模型基础上,根据对SM→STM→LTM忆阻器的感觉记忆阶段特点的分析,设计了SM→STM→LTM忆阻器模型.所设计的模型包括基于状态的伏安方程(1)以及状态方程(2),(3),(4),(12).本节通过仿真分析来验证前文所设计的忆阻模型对于SM→STM→LTM忆阻器特性的描述能力.状态变量w的变化能够反映出忆阻器阻值的变化情况,因此在后面的仿真中将用w的变化来反映忆阻器记忆的形成与遗忘.
仿真中模型参数取值:b+=30,τw+=0.16 s,τmin0= 10000 s,τmin+= 0.3 s,kτ+= 3,τw0_min=0.9 s,τw0_max=3 s,k=1,ka+=1.1,amin=0.5 V-1,amax=2 V-1;这里所讨论的仿真过程中不存在负电压的作用,因此参数τw-,a-,b-,τmin-,kτ-,ka-可取任意值. 仿真初始时刻,各状态变量均处于其下限.
图5给出了SM→STM→LTM忆阻模型的状态变量在连续脉冲激励作用下的变化曲线.图5(a)为该过程中所施加的连续脉冲激励,脉冲幅值Vamp为1 V,宽度为0.1 s,间隔为0.5 s,脉冲间隔期间的电压大小为Vlow+=0.1 V;图5(b)—(e)为模型的各个状态变量在该过程中的变化.
在初始4个脉冲作用时,a+虽然逐渐增大,但脉冲幅值始终小于1/a+,图6中紫色曲线为第2个脉冲作用时(t=0.65 s)Fw关于输入电压V的曲线,此时的脉冲作用下w将向着Fw≈4.8×10-6变化,因此在这一脉冲作用下w没有明显的变化,忆阻器此时处于感觉记忆阶段,在这一阶段的脉冲作用下忆阻器没有明显的记忆形成,状态变量wmin和τw0也没有明显变化.
后续的3个脉冲作用下,a+的继续增长使得1/a+逐渐小于脉冲幅值,图6中蓝色曲线为第6个脉冲作用时(t=3.05 s)Fw关于输入电压V的曲线,此时的脉冲作用会使得w趋向于Fw≈0.95,在这一脉冲作用下能观察到w的明显增大,忆阻器有明显的记忆形成;在此阶段的脉冲激励作用下τw0也开始逐渐增长,而wmin仍然无明显变化;图7中蓝色曲线为经历7个脉冲激励作用后,若不再施加更多脉冲激励(作用电压恒为Vlow+),状态变量w的归一化曲线,此时w将快速递减并在0附近逐渐收敛,由这一过程中w的变化可以看出,经历7个脉冲激励后所形成的记忆主要是短期记忆.

图5 连续脉冲激励作用下模型状态变量的变化 (a)所施加的连续脉冲激励;(b)—(e)依次为状态变量w,wmin,τw0,a+在该过程中的变化曲线Fig.5.The variation of state variables when a series of positive pulses are applied:(a)The applied pulse;(b)–(e)the variation of w,wmin, τw0,and a+during this process.
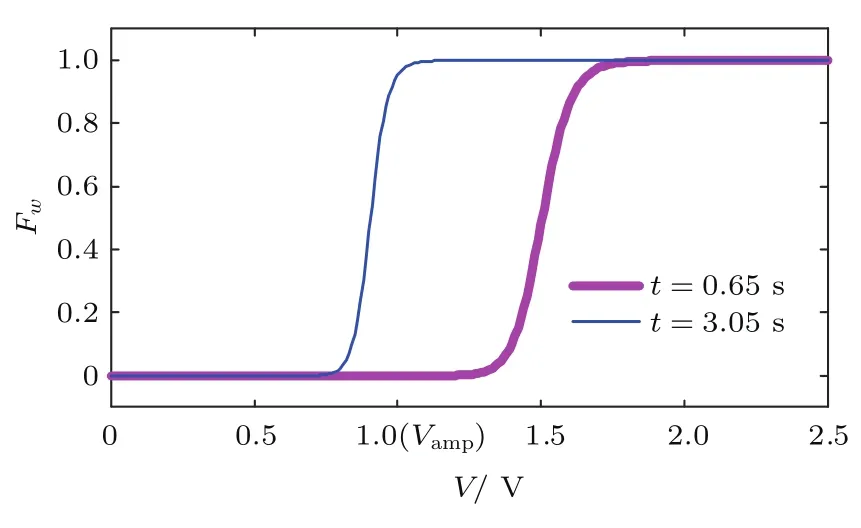
图6 第2个脉冲(t=0.65 s)、第6个脉冲(t=3.05 s)作用时Fw关于电压V的曲线,所施加脉冲的幅值电压大小在图的横坐标中用Vamp标出Fig.6.Curves of Fwwith respect to V at the time when the 2nd pulse(t=0.65 s)and the 6th pulse(t=3.05 s)are applied.Vampis the amplitude of the applied pulses.
在之后的脉冲激励作用下,所有的状态变量都会有所增长:a+的继续增长使w,wmin,τw0保持了脉冲作用下逐渐增长的变化趋势;w将继续增长并逐渐接近其上限;τw0的继续增长使得脉冲间隔期间w的递减更为缓慢;wmin在这一阶段的脉冲激励作用下也开始有了明显的增长.若经历8个、9个脉冲激励后不再施加更多脉冲(作用电压恒为Vlow+),状态变量w的归一化变化曲线如图7中红色、黄色曲线所示.所形成的记忆中,一部分会被较快遗忘,这部分记忆仍然为短期记忆;而另一部分记忆可持续存在较长时间,这部分记忆为长期记忆.对比上述两条遗忘曲线可看出,更多的脉冲激励作用下可使得更多的短期记忆转化为长期记忆.
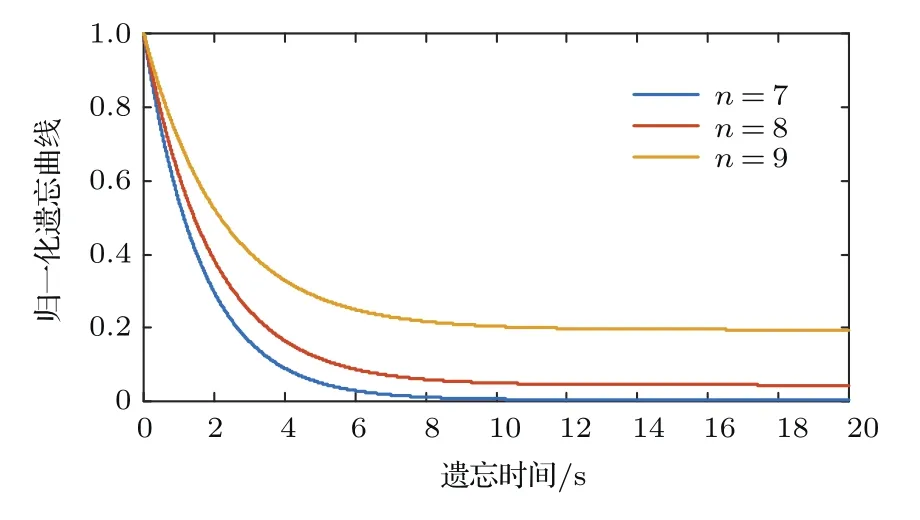
图7 经历n个脉冲激励作用后的遗忘曲线(n=7,8,9)Fig.7. Forgetting curves after applying n pulses(n=7,8,9).
图8 给出了在不同幅值、宽度、间隔的脉冲作用下,状态变量w的变化情况.图8(a)中所施加的脉冲分别与图8(b)—(d)中所施加脉冲的宽度、幅值、间隔有所不同.当脉冲幅值为0.9 V、宽度为0.08 s、间隔为0.6 s时,如图8(a)所示,初始6个脉冲作用时,w无明显变化,此时忆阻器处于感觉记忆阶段,后续的脉冲作用下可观察到w的明显增长,忆阻器的记忆逐渐形成;当脉冲宽度增大为0.16 s,脉冲幅值、间隔不变,如图8(b)所示,感觉记忆阶段所经历的脉冲数量减少为3个,并且从第4个脉冲开始,在每次的脉冲作用下所形成的记忆增量更大,经历12个脉冲作用后w保持在其上限附近,脉冲宽度的增大意味着每个脉冲周期内脉冲电压的作用时间更长,因此该过程中记忆的形成速度更快;当脉冲幅值增大为1.75 V,脉冲宽度、间隔不变时,如图8(c)所示,在第1个脉冲激励作用时就能够观察到w的增长,后续脉冲的连续作用下w逐渐增长至其上限附近,在这一过程中,由于脉冲幅值较大,脉冲作用时1/a+会较快递减至小于脉冲幅值的位置,因此该过程中并没有感觉记忆阶段,初始脉冲作用时就可观察到有明显的记忆形成;当脉冲间隔增大为9 s,脉冲幅值、宽度不变时,如图8(d)所示,有明显的记忆形成后,记忆随脉冲激励的形成速度与图8(a)相比明显较慢,并且在脉冲间隔期间可观察到短期记忆从快速下降到逐渐收敛的遗忘过程,经历的脉冲数量越多,短期记忆的遗忘过程越缓慢,遗忘曲线的收敛值越大.对比图8(a)和图5(b)的仿真结果可以看出,若同时增大所施加脉冲的幅值与宽度,并减小脉冲间隔,则感觉记忆阶段经历的脉冲数量更少,开始有记忆形成后,记忆形成的速度更快.

图8 不同幅值、宽度、间隔的脉冲作用下状态变量w的变化各实验中所施加的脉冲参数分别为:(a)幅值 =0.9 V,宽度=0.08 s,间隔 =0.6 s;(b)幅值 =0.9 V,宽度 =0.16 s,间隔 =0.6 s;(c)幅值 =1.75 V,宽度 =0.08 s,间隔 =0.6 s;(d)幅值 =0.9 V,宽度 =0.08 s,间隔 =9 s;横坐标中的T为脉冲周期,T=宽度+间隔Fig.8. The variation of w when the input voltage is 17 pulses with different amplitude,interval,and duration:(a)Amplitude=0.9 V,duration=0.08 s,interval=0.6 s;(b)amplitude=0.9 V,duration=0.16 s,interval=0.6 s;(c)amplitude=1.75 V,duration=0.08 s,interval=0.6 s;(d)amplitude=0.9 V,duration=0.08 s,interval=9 s;T is the period of the applied pulse signal,T=duration+interval.
5 状态变量的物理意义
这类忆阻器的阻变机理通常可用外加电压作用下两电极间导电通道的形成与消失来解释[2,3,5,8,14-19],图9给出了外加电压作用下导电通道的变化过程.初始时刻忆阻器处于高阻状态,两电极间无导电通道,如图9(a)所示;外电压作用下,金属原子在两电极间逐渐累积生长,未连通两电极之前,两电极间的阻值无明显变化,如图9(b)所示,此时忆阻器处于感觉记忆阶段;在外加电压的持续作用下,累积生长的导电通道将连通两电极并逐渐增宽,两电极间的阻值逐渐减小,如图9(c)和图9(d)所示.外电压作用下所形成的导电通道包括稳定和不稳定两部分,导电通道的稳定部分形成忆阻器的长期记忆,移除外电压后这部分导电通道可持续存在较长时间,导电通道不稳定部分形成忆阻器的短期记忆,外电压移除后这部分导电通道会较快分解消失.若忆阻器处于图9(c)所示状态之后移除外加电压,导电通道不稳定部分的分解消失将使得忆阻器回到高阻状态,如图9(e)所示,这一过程对应于图7中蓝色曲线所示过程;若忆阻器处于图9(d)所示状态之后移除外加电压,导电通道不稳定部分分解消失后,导电通道稳定部分仍然连通忆阻器的两个电极,如图9(f)所示,这一过程与图7中的红色、黄色曲线所示过程对应.

图9 忆阻器两电极间导电通道的变化过程 (a)—(d)连续外电压作用下两电极间导电通道的生长过程;若忆阻器处于(c)和(d)所示状态后不再继续施加外电压,导电通道的不稳定部分将逐渐分解消失,最终分别只剩下(e)和(f)所示的导电通道稳定部分Fig.9.Schematic illustration of the change of the conductive channel:(a)–(d)The growth of the conductive channel when the voltage is continuously applied.If the applied voltage is removed after memristor reaches the state as shown in(c)and(d),the unstable part of the conductive channel would be gradually annihilated,and the stable part would exist as shown in(e)and(f),respectively.
在前文所讨论的SM→STM→LTM忆阻模型中,w可理解为导电通道的归一化面积,wmin为导电通道稳定部分的归一化面积,τw0描述了导电通道不稳定部分在遗忘过程中消失的快慢.(1/a+)∈[(1/amax),(1/amin)]与施加在忆阻器两端的正电压之间的大小关系决定导电通道在外加电压作用下的变化:初始时刻忆阻器处于高阻状态,若正电压幅值明显小于1/amax时(例如所施加的正电压为Vlow+),连接两电极的导电通道将无法形成,此时w,wmin,τw0均无明显的变化,忆阻器阻值始终较大;在大于1/amax的电压作用下,初始阶段金属原子首先逐渐累积,此时V<1/a+,连通两电极的导电通道尚未形成,在此阶段w,wmin,τw0任然没有明显变化,a+在正电压作用下的逐渐增长将使得在电压作用一段时间后V>1/a+,此时连接两电极的导电通道已形成,忆阻器阻值明显减小,w,wmin,τw0将会逐渐增大;所施加的正电压越大,a+增长的速度越快,导电通道形成过程所需时间(即w,wmin,τw0无明显变化阶段所经历的时间)越短.
6 结 论
本文在文献[25]所提出的STM→LTM忆阻模型的基础上,根据文献[17—19]中所报道的SM→STM→LTM忆阻器的记忆与学习特性,设计了SM→STM→LTM忆阻器的数学模型.由模型的仿真分析可以看出,所设计的SM→STM→LTM忆阻模型保留了原STM→LTM模型对于短期记忆和长期记忆的描述能力,同时也能够描述SM→STM→LTM忆阻器的感觉记忆过程.模型状态变量的物理意义可用忆阻器两电极间的导电通道的形成与消失来解释.本文的模型可用于这类忆阻器的进一步的理论分析与应用设计.
