单光子调制频谱用于量子点荧光寿命动力学的研究∗

张强强 胡建勇 景明勇 李斌 秦成兵†李耀 肖连团‡ 贾锁堂

1)(山西大学激光光谱研究所,量子光学与光量子器件国家重点实验室,太原 030006)

2)(山西大学极端光学协同创新中心,太原 030006)

(2018年10月5日收到;2018年11月7日收到修改稿)

本文开展了基于单光子调制频谱测量量子点荧光寿命动力学特性的研究.在脉冲激光激发下,对探测到的量子点单光子荧光信号进行频谱分析以获得荧光调制频谱,研究发现特征频谱信号幅值与荧光寿命之间存在确定的非线性对应关系.这种单光子调制频谱方法能有效消除背景噪声和单光子探测器暗计数的影响,用于分析量子点荧光寿命动力学特性时在准确度以及时间分辨率方面都较目前普遍采用的荧光衰减曲线寿命拟合方法呈现出明显优势:当涨落误差为5%时,寿命测量准确度提高了一个数量级;当涨落误差和偏离误差均为5%时,对动力学测量效率以及时间分辨率提高了四倍以上.因此单光子调制频谱可以作为获取量子点在短时间尺度内激发态动力学信息的一种有效技术手段.

1 引 言

量子点作为一种新型荧光和光电材料,因其所具有的独特的物理性质,如宽带吸收、窄带荧光发射、荧光波长连续可调、高量子产率以及良好的光化学稳定性和电荷传输特性[1]等而被广泛研究.特别是量子点在太阳能电池[2-4]、发光二极管[5,6]、光电探测器[7]、双光子源[8]、激光器[9,10]以及生物医学标记等[11-13]方面都得到了广泛应用.荧光寿命在研究量子点发光机理以及调控其动力学过程中发挥着重要作用,通过分析荧光寿命,可以获得辐射复合和非辐射复合等动力学过程中单激子、电离态和双激子的成分及影响[14,15],还可以用来研究俄歇复合或俘获态引起的量子点荧光闪烁[16-23]以及通过量子点与周围环境的电荷转移或荧光共振能量转移调控量子点荧光辐射特性等[24,25].而对量子点激发态寿命的有效调控[26]可以用于研究异构化发生的位点、反应通道和时间等非绝热动力学.

目前获取量子点荧光寿命普遍采用的方法是时间分辨荧光光谱,即基于时间相关单光子计数(time-correlated single-photon counting,TCSPC)的荧光衰减曲线寿命拟合法( fluorescence decay curve fitting,FDCF)[14-20].该方法首先通过TCSPC技术记录每个荧光光子的到达时间,然后提取若干脉冲周期中到达时间的统计分布,获得时间分辨荧光衰减曲线,最后根据相应的物理过程使用单指数或多指数通过最小二乘法拟合荧光衰减曲线,从而获得荧光寿命.然而,实验系统中存在背景光子和暗计数等噪声[27],由此引起的额外光子计数同样会累计在荧光衰减曲线上,导致通过FDCF获取的荧光寿命存在一定误差.为了降低误差,获得更为准确的荧光寿命,实验中需要对足够多的光子进行拟合,这意味着更长的积分时间,因而无法提取更小时间尺度内的动力学信息.

本文提出了一种单光子调制频谱技术(single photons modulation spectrum,SPMS)用于荧光寿命测量.该技术利用脉冲激发光的重复频率对荧光光子在时域上的内禀调制作用,通过对单个荧光光子的到达时间进行频谱分析,再基于调制频谱信号幅值与荧光寿命的关系,从而获得量子点的荧光寿命.该方法所采用的单光子调制技术能有效克服噪声干扰[28,29],因此可获得具有高信噪比的调制频谱信号.

在本文中,我们首先从理论上推导了调制频谱信号幅值与量子点荧光寿命的关系;然后通过对比FDCF与SPMS两种方法所获得的量子点荧光寿命来说明SPMS方法的可靠性,通过比较两种方法的误差来说明SPMS的优越性;最后利用SPMS获得的实时荧光寿命轨迹研究了量子点在亚秒量级下的动力学特性.本文所用方法的显著特点是抗噪声能力强,可高效获得高时间分辨率的荧光寿命,为研究短时间尺度内的动力学过程提供了一种新的手段.

2 单光子调制频谱理论分析

量子点发出的荧光光子相对于激发脉冲的时间延迟服从指数衰减分布[1],基于TCSPC技术可以获得反映该分布的荧光衰减曲线.为了准确获得每一个光子的时间延迟,将脉冲重复周期均匀地分为m个光子计数通道,每个通道宽度为∆t(实验中取决于TCSPC设备的时间分辨能力),如图1(a)所示.通道数与通道宽度满足m×∆t=T0,其中T0为激光脉冲重复周期.对各个时间通道的光子计数进行累积便形成了荧光衰减曲线,如图1(b)所示.当一定时间内的荧光光子来自量子点同一种动力学行为时,其在各时间通道内的光子数分布服从某一寿命τ对应的单指数衰减函数[1],可表示为

其中y0为荧光光子数分布函数;tr为荧光光子相对激发脉冲的时间延迟;A即指前因子,为tr等于0时的荧光光子数.基于该分布函数,y0与总荧光光子数N0具有如下关系:

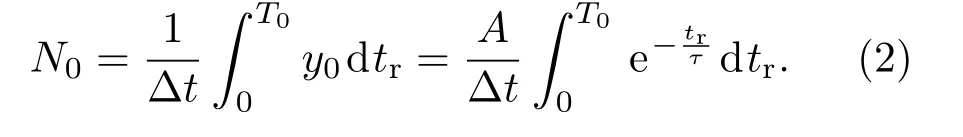
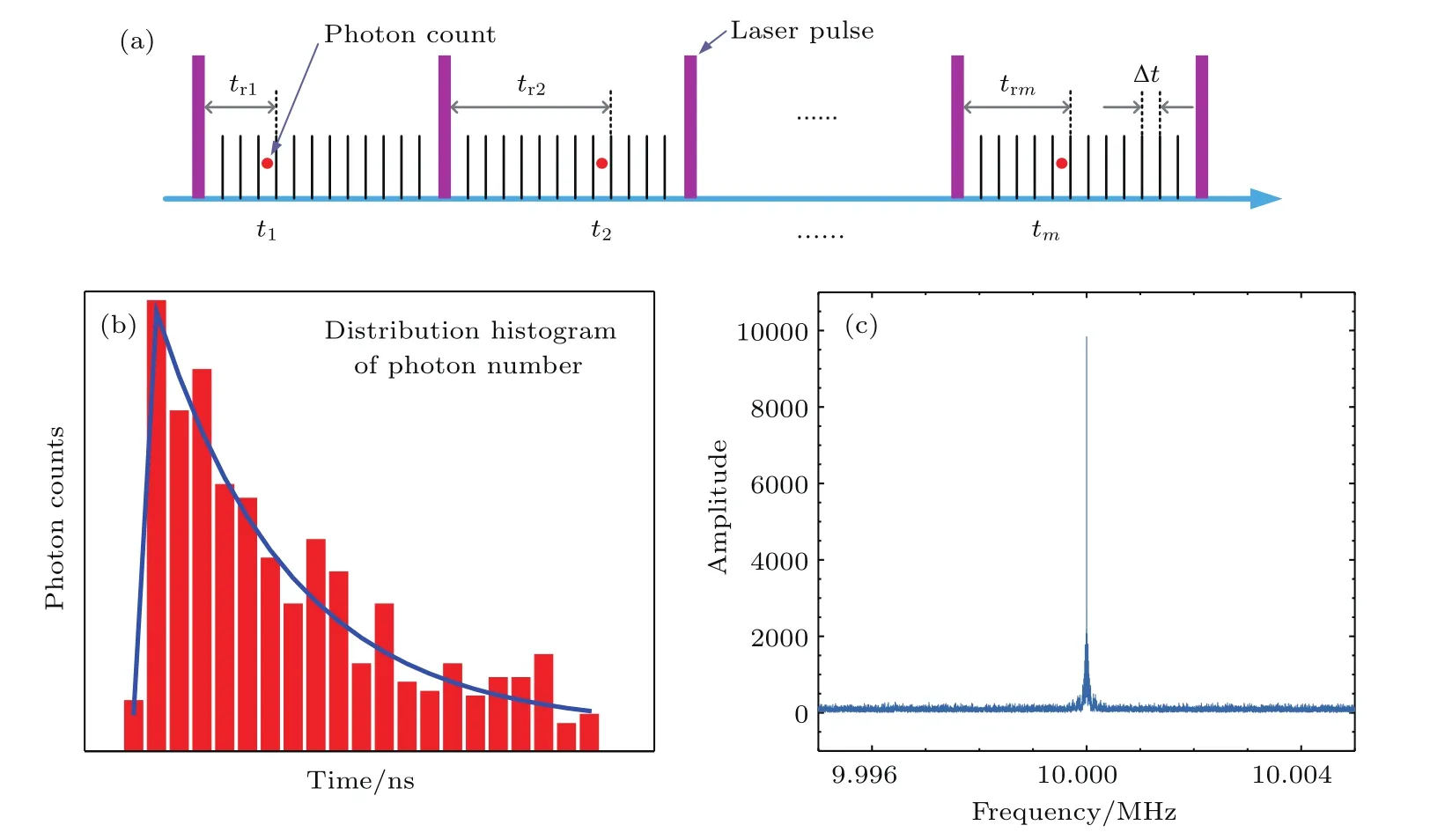
图1 单光子调制频谱原理示意图 (a)基于TCSPC的单光子检测时序图;(b)通过TCSPC获取荧光衰减曲线原理示意图;(c)单光子调制频谱模拟结果,激发脉冲频率为10 MHz,光子计数为10000Fig.1.Schematic diagram of single photons modulation spectrum(SPMS):(a)TCSPC-based single photons detection timing diagram;(b)schematic diagram of fluorescence decay curve obtained by TCSPC;(c)simulation of SPMS with excitation pulse frequency of 10 MHz and photon counts of 10000.

由此可知,指前因子可表示为

代入(1)式,则有

由(4)式可知,荧光光子数分布函数y0与总荧光光子数N0、荧光寿命τ、相对延迟tr、通道宽度∆t以及脉冲重复周期T0有关,其中∆t和T0一般是确定的,因此y0可以记为y0(tr,τ,N0).考虑到受仪器响应函数I(tr)的影响,实际的荧光光子数分布Y(tr,τ,N0)是y0(tr,τ,N0)和仪器响应函数I(tr)的卷积[30],可表示为

此外,光子数分布函数还受暗计数和背景光子的影响.实验中暗计数是由探测器将电子噪声误判为荧光信号所导致的,而背景光子则来自环境中的杂散光,这两种噪声均服从泊松分布,因此在频域上表现为白噪声分布[28].而借助单光子调制技术则可以有效抑制白噪声背景,得到高信噪比调制频谱信号.图1(c)是通过理论模拟得到的单光子调制频谱,在模拟中,信号频率(脉冲光重复频率)为10 MHz,总光子计数为10000,其中白噪声光子计数为1000,可以看到,获得的频谱信号幅值具有极高的信噪比.

暗计数和背景光子在各时间通道的分布函数yd和yb可以分别表示为:

其中nd为暗计数率,nb为背景光计数率,ta为总光子数N对应的分析积分时间.选取的总分析光子数N等于荧光光子数和噪声光子数之和,

进一步地,如图1(a)所示,当第i个荧光光子在第m个脉冲周期到达时,其绝对到达时间ti可表示为

其中tri为该荧光光子的相对延迟.对每个光子的到达时间ti做离散傅里叶变换,可以得到其频率谱X(f)[31],

其中,α为探测器输出脉冲的幅值,f为频率.对于单光子探测器,每次探测到信号输出的幅值相同,因此可简化为α=1.对于脉冲重复频率f0,其频谱信号幅值可以表示为

其中f0和T0满足

以∆t为通道宽度,将脉冲重复周期T0分成T0/∆t个时间通道,光子相对延迟tr分布在各时间通道中,受限于TCSPC设备的时间分辨能力,每个时间通道中的所有光子对应同一相对延迟tr,则频谱信号幅值可表示为

其中k和nk分别表示通道序数和第k个时间通道中的光子数,分别满足:

其中,ybk(ta)和ydk(ta)分别为第k个时间通道中两种噪声的光子数.在第k个时间通道中tr表示为(k-1/2)∆t.将(15)式代入(13)式,则脉冲重复频率f0位置处的频谱信号幅值X(f0)可以表示为

其中C为理论修正常数.

对于稳定的实验系统,其仪器响应函数I(tr),背景计数率nb,暗计数率nd均为常数.因此当积分时间ta以及总光子数N确定后,即可根据(16)式,由荧光寿命τ得到脉冲重复频率的频谱信号幅值X(f0),反之,亦可由傅里叶变换获得的频谱信号幅值X(f0)得到荧光寿命τ.

3 实验方法

实验中所用量子点是CdxZn1-xSeyS1-y/ZnS核/壳结构量子点(张家港海纳至精新材料科技有限公司),尺寸为9.1 nm,发射峰为515 nm.取10µL量子点原液放入离心管内再加入适量甲苯溶液,然后将离心管放入超声波清洗器中超声振荡2 min,再放在摇匀机上摇匀2 min后配制成量子点浓度约10-9mol/L的量子点溶液,最后将其用匀胶机以3000 r/min的转速旋涂于洗净的SiO2玻片上.

实验装置图见参考文献[23].实验中所使用的激发光是超连续脉冲激光器(WL-SC-400-15-PP,NKT Photonics,脉宽70 ps)发出的406 nm波长脉冲激光.激光用油浸物镜(Nikon,100×,1.3 NA)聚焦到量子点样品上激发荧光,经过二向色镜(Semrock),发射滤波片和100µm针孔后,荧光接着通过50/50分束棱镜分成两束.两台单光子探测器(SPCM-AQRH-16-FC,Excelitas)用来同时探测两束荧光,探测器输出端接入时间间隔分析仪(HydraHarp 400,PicoQuant)记录每个荧光光子的到达时间.实验中脉冲重复频率设为10 MHz,暗计数率nd为每秒100个(cps),背景光子计数率nb为800 cps.

为了获得具有不同动力学行为的量子点荧光轨迹,实验中采用三种不同的激发光功率密度对量子点进行激发.本文中量子点QD1,QD2和QD3对应的激发光功率密度分别为61.7,11.9以及20.6 W/cm2.

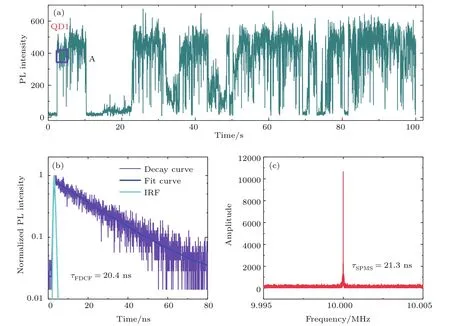
图2 基于FDCF和SPMS的荧光寿命测量 (a)量子点QD1的荧光轨迹;(b)单指数函数拟合的荧光衰减曲线,对应荧光轨迹中的位置A,图中IRF为仪器响应函数,拟合所用光子数为20000;(c)位置A处的单光子调制频谱图,频谱信号频率为10 MHz,光子数为20000Fig.2.Fluorescence lifetime measurement based on FDCF and SPMS:(a)PL intensity time trajectory of quantum dot QD1;(b) fluorescence decay curve fitted by single exponential function of area A in(a)with photon number of 20000,IRF in the figure indicates the instrument response function;(c)single photons modulation spectrum diagram of area A with spectrum signal frequency of 10 MHz and photon number of 20000.

4 实验结果与讨论

4.1 量子点荧光的FDCF和SPMS测量

分别使用FDCF和SPMS对量子点QD1产生的荧光进行寿命分析.从图2(a)所示的荧光轨迹中可以发现,在61.7 W/cm2的激发光功率密度下QD1的荧光强度(photoluminescence intensity,PL intensity)随时间变化较大,存在明显的荧光闪烁现象,这是因为在高激发功率下,量子点内部会发生电离和去电离等多种动力学过程[15],从而形成荧光闪烁.

由于(16)式描述的是单一动力学过程中信号幅值与荧光寿命的关系,因此通过SPMS分析荧光寿命时,需要确保所分析光子中仅包含单一动力学过程.对于单一动力学过程,其荧光衰减曲线可以用单指数函数拟合,因此我们在时间轨迹上选取可用单指数函数拟合的区域,如图2(a)中方框区域A所示.一方面对区域内的光子通过FDCF获取其荧光寿命,如图2(b)所示,通过单指数函数拟合得到的寿命为20.4 ns;另一方面通过傅里叶变换得到该区域内光子的频谱信号幅值,如图2(c)所示,再由(16)式获得荧光寿命,结果为21.3 ns,即为SPMS的寿命分析结果.

4.2 误差分析

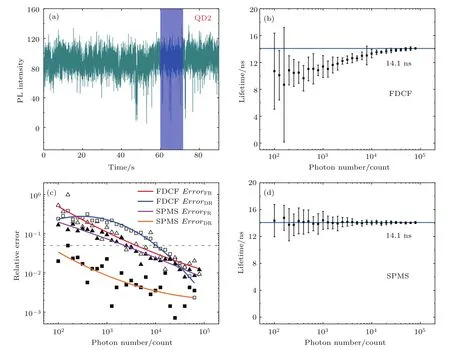
图3 FDCF和SPMS的误差分析比较 (a)量子点QD2的荧光轨迹,阴影部分为所选取的分析区域;(b)FDCF所得寿命和光子数的关系;(c)两种方法所得寿命的涨落误差(ErrorFR)与偏离误差(ErrorDR)和光子数的关系,图中虚线处相对误差值为5%;(d)SPMS所得寿命和光子数的关系Fig.3.Comparison of errors of FDCF and SPMS:(a)PL intensity time trajectory of quantum dot QD2,the shaded section is the selected analysis area;(b)relationship between the lifetimes of FDCF and the photon number;(c)relationship between fluctuation errors(ErrorFR)and deviation errors(ErrorDR)of lifetimes and photon number of the two methods respectively,the relative error at the dotted line in the figure is 5%;(d)relationship between the lifetimes of SPMS and the photon number.

为了比较FDCF和SPMS在量子点荧光寿命分析上的差异性,我们分别使用两种方法对量子点QD2的荧光轨迹上同一区域进行分析.量子点QD2的荧光轨迹如图3(a)所示,可以发现,在11.9 W/cm2的激发光功率密度下,QD2的荧光闪烁被有效抑制,量子产率趋于稳定,表明量子点在该条件下只包含单一动力学过程.在QD2的荧光轨迹上选取一段区域后,如图3(a)中阴影部分所示,区域整体的荧光衰减曲线可以用单指数函数拟合,进一步表明QD2仅包含单一动力学过程.在该区域中我们依次选取不同数量的光子进行寿命分析,以FDCF为例,具体过程是多次选取数量固定的光子,对其进行寿命分析,并得到寿命的平均值和涨落.然后,改变分析光子数,重复进行FDCF分析和数据处理,最终得到不同光子数下的FDCF分析结果,如图3(b)所示.同理可以得到不同光子数下的SPMS分析结果,如图3(d)所示.考虑到光子数足够多时(80000以上),其荧光寿命固定在14.1 ns,因此可以认为14.1 ns是该区域量子点寿命的真值.从图3(b)中可以看出,对于FDCF,当光子数较低时,平均寿命与寿命真值有较大偏离,同时荧光寿命涨落明显.而图3(d)的实验结果显示,对于SPMS,在不同光子数下得到的平均寿命都基本稳定在14.1 ns附近,另外寿命涨落也相对较小.这里误差来自寿命的涨落以及平均寿命与寿命真值的偏离两方面.

为了进一步分析和比较两种方法的误差,分别用涨落误差ErrorFR和偏离误差ErrorDR表示上述两方面误差:

其中∆τf表示荧光寿命涨落,表示平均寿命,∆τd表示平均寿命对寿命真值τs的偏离.在图3(c)中分别给出了FDCF和SPMS的这两种误差,可以发现SPMS的涨落误差ErrorFR在各光子数水平下都小于FDCF,且SPMS的偏离误差ErrorDR也明显小于FDCF.因此,与FDCF相比,SPMS在荧光寿命测量准确度上展示出明显的优势,其对抗噪声干扰的能力得到了很大提升.此外,在图3(c)中,当ErrorFR为5%(2σ)时,如虚线所示,FDCF对应的光子数为4016,SPMS对应的光子数为2298,即当ErrorFR为5%时,FDCF所需的光子数近乎达到SPMS所需光子数的两倍.然而,在该光子数水平下,对于FDCF而言,ErrorDR高达11.7%,而对于SPMS,ErrorDR则仅为0.59%,因此,相比于FDCF,SPMS获取荧光寿命的准确度提高了一个数量级以上.另外,当ErrorFR和ErrorDR均达到5%时,FDCF所需的光子数为10289,SPMS所需的光子数为2298,不足前者的1/4.而在无明显荧光闪烁时,荧光光子数和积分时间成正比,即ErrorFR和ErrorDR皆为5%时,SPMS的寿命获取效率和时间分辨率相较FDCF提高了至少四倍.

图4 FDCF和SPMS对不同寿命的分析结果对比 (a)信号幅值和荧光寿命的关系,光子数20000;(b)FDCF和SPMS所得寿命对比,线性拟合斜率0.997;(c)两种方式所得寿命的差值分布Fig.4.Comparison of analysis results of FDCF and SPMS for different lifetimes:(a)Relationship between signal amplitude and fluorescence lifetime with photon number of 20000;(b)comparison of lifetimes obtained by FDCF and SPMS with linear fitting slope of 0.997;(c)distribution of lifetime difference between FDCF and SPMS.

SPMS测量荧光寿命时在涨落误差和偏离误差都明显优于FDCF的测量结果,其内在原因可以通过以下两方面来解释.首先涨落误差主要由散粒噪声导致,此类噪声的标准偏差等于平均光子数N的平方根,即为所造成的涨落误差则表现为可见,当光子数增大时涨落误差随之减小,如图3中FDCF和SPMS结果所示.另外,由于最小二乘法拟合本身的原理限制,即使在分析同一组数据时,FDCF每次的拟合结果都会有一定差异,从而导致额外的涨落误差.而SPMS通过调制频谱信号幅值与荧光寿命之间的解析表达来获得量子点寿命,通过同一组数据对应的唯一信号幅值即可获得确定的荧光寿命结果,因此SPMS的涨落误差小于FDCF.对于偏离误差,由于最小二乘法的拟合优度极大地依赖于数据点数,因此FDCF荧光寿命测量结果的准确性直接取决于用于分析的光子数:当光子数水平较低时,FDCF得到的寿命结果表现出与寿命真值的明显偏离.而SPMS具有抗噪声干扰的特性,即使在弱光条件下也同样能实现对信号幅值的准确获取,故而荧光寿命的偏离误差较小.

在对呈现单一寿命的量子点QD2的荧光轨迹进行误差分析后,我们使用FDCF和SPMS对包含多种寿命的量子点QD1的荧光轨迹(在一定的积分时间之内仍然可以很好地使用单指数进行拟合)进行了比较分析,结果如图4所示.图4(a)中空心点为FDCF分析结果(每次拟合所用光子数为20000),实线为根据(16)式计算获得的结果,可以看出荧光寿命和频谱信号幅值呈非线性关系,实验结果和理论计算相符合.为进一步比较FDCF和SPMS所得结果,对二者进行了相关性分析,如图4(b)所示,该相关性可以很好地使用线性拟合,且拟合曲线斜率为0.997,说明SPMS的可靠性.由图4(c)可以看出二者的寿命差值最大为1 ns.由图3的误差分析结果可以很容易理解产生误差的原因来自较低光子数(20000)下的寿命偏离与涨落.

4.3 通过SPMS测量量子点的荧光寿命动力学特性

由前文分析可知,SPMS能够高效地获取荧光寿命,相应地对动力学变化过程具有较高的分辨率.因此SPMS可用于实时测量量子点的荧光寿命动力学特性.所测量的量子点QD3的荧光轨迹如图5(a)所示,可以看出,在20.6 W/cm2的激发光功率密度下,QD3的荧光闪烁剧烈程度介于QD1和QD2之间,因此QD3虽然包含多种动力学过程,但其动力学复杂度要小于QD1.对QD3的荧光轨迹使用SPMS分析其寿命,每次分析所用光子数为2298,对应图3(c)中5%的涨落误差ErrorFR以及0.59%的偏离误差ErrorDR.分析结果如图5(b)所示.对比图5(a)和图5(b)可以发现,在荧光轨迹上即使量子产率相同的区域,其荧光寿命也存在较大的变化和差异.在23 s到30 s之间,从荧光轨迹中可以观察到荧光量子产率大致趋于一个固定值,然而在具有亚秒量级时间分辨率的荧光寿命轨迹中却呈现出较大的变化,意味着在这段时间内量子点内部发生了多个动力学过程.可见,通过SPMS获得的荧光寿命轨迹可以实时反映在荧光轨迹上无法观察到的寿命动力学特性信息,同时具有相当高的时间分辨率.

图5 基于SPMS对量子点荧光寿命动力学特性的实时表征 (a)量子点QD3的荧光轨迹;(b)通过SPMS获取的荧光寿命轨迹,每次分析所用光子数为2298Fig.5.Real-time characterization of fluorescence lifetime dynamics of quantum dot based on SPMS:(a)PL intensity time trajectory of quantum dot QD3;(b) fluorescence lifetime trajectory obtained by SPMS with photon number for each analysis of 2298.

5 结 论

本文利用SPMS和FDCF对量子点的荧光寿命进行了比较测量.实验结果显示通过SPMS测得的荧光寿命在涨落误差和偏离误差两方面都明显优于FDCF的测量结果,因此可以实现极高的荧光寿命测量准确度.当涨落误差为5%时,荧光寿命准确度提高一个数量级以上;在同等测量误差水平下,SPMS获得荧光寿命所需的光子数明显小于FDCF,故可显著提高荧光动力学测量的效率以及时间分辨率,当涨落误差和偏离误差均为5%时,测量效率和时间分辨率提高了四倍以上.基于SPMS能够实现快速和高时间分辨率的荧光寿命获取,利用SPMS在低光子数水平下获得了快速的量子点荧光寿命轨迹,对量子点在亚秒尺度内的动力学特性进行了直观表征.这种SPMS方法可用于抗噪声干扰且高准确度和高时间分辨率的荧光寿命动力学研究,例如可用于通过光致还原调制氧化石墨烯荧光寿命[32]以及利用荧光寿命揭示单层氧化石墨烯光致还原动力学的研究等[33].因此SPMS为研究短时间尺度下单量子体系荧光动力学行为提供了有效技术手段.