基于振型转角改变的框架梁损伤检测研究
2019-01-23袁艺宸
李 林, 袁艺宸
(1.福建江夏学院 工程学院,福州 350108; 2.华中科技大学 土木工程与力学学院,武汉 430074)
框架结构是广泛使用的结构体系,探索简便有效的框架结构损伤检测方法具有重要意义。由于结构模态易于通过自由振动、强迫振动以及环境振动等数据提取,因而基于结构模态数据改变的损伤检测得到了广泛的研究[1-2]。Hu等[3]提出了基于交叉模态应变能的结构损伤诊断方法,该方法具有所需结构损伤后模态信息少的优点,但是,该方法需要预先假设损伤位置,然后进行验证,当结构较复杂且发生多处损伤时,可能的损伤组合数量巨大,在实施上存在困难。Roy等[4]用摄动法导出了结构一阶振型及其导出量与结构损伤位置间的关系,该方法主要用于损伤定位。Ghosh等[5]研究了结构高阶振型与结构损伤位置的关系,研究表明框架结构高阶振型对损伤位置判别的有效性与损伤的位置密切相关。针对剪切型框架,Koo等[6-8]根据柔度矩阵可利用结构低阶模态合成的特点,利用模态柔度计算得到的层间位移改变识别了结构损伤。Zhu等[9]研究了剪切型框架结构层间刚度损失的检测方法,该方法仅仅需要测试结构的一阶振型平移,就能够识别损伤所发生的层和损伤程度,表明利用结构低阶模态信息能够有效检测结构损伤,这对于实际工程具有很好的适用性。
剪切型框架横梁刚度无穷大,荷载作用下梁端不会产生转角,损伤识别时也不存在识别梁损伤的问题。而实际的框架结构横梁刚度有限,当结构发生损伤时,损伤不仅会造成结点平动位移的变化,还会造成结点转动位移的变化。随着传感技术的进步,转角加速度传感器不断发展[10-11],从而为直接获得振动转角数据提供了可能,通过监测结构损伤前后转动位移的变化有可能实现结构的损伤检测。Abdo等[12]通过对损伤梁和板的数值分析表明,振型转角是敏感的损伤定位指标,同时具有良好的鲁棒性。Kokot等[13]采用优化方法研究了简谐荷载作用下两跨连续梁和单层单跨框架的损伤识别问题,研究表明,在检测中增加转角数据能够实质性地改进损伤识别的结果,特别是当测试数据中包含噪声时,效果更为显著。上述研究中的研究对象均为单个构件或简单结构,将这些损伤检测方法应用于多层多跨框架结构还存在较大困难。
“强柱弱梁”是框架结构设计的原则之一,合理设计的框架结构梁先于柱发生损坏,及时检测框架梁的损伤并进行维护能够有效保证结构的抗灾能力。敏感性分析是结构分析中的常用方法,通过敏感性分析可实现检测结构损伤[14]、有限元模型修正[15]等目的。本文以多层多跨框架结构为研究对象,以损伤前后梁柱节点振型转角改变为损伤指标,在对梁柱节点振型转角敏感性分析的基础上进行框架梁损伤位置和损伤程度识别研究。
1 振型转角敏感性分析
结构的矩阵特征值问题有以下表达形式
(1)
式中,K和M分别是刚度矩阵和质量矩阵,ωi是第i阶圆频率,φi是第i阶振型。
对于平面框架结构,每个梁柱节点有2个平动自由度和1个转动自由度。忽略梁柱的轴向变形,则对于一个n层m跨的平面框架具有n个平动自由度和n×(m+1)个转动自由度。为便于分析,对结构进行自由度编号时可先对平动自由度从下向上编号,然后对转动自由度从下向上、从左向右进行编号,一榀五层三跨框架自由度编号如图1所示。图中,u1~u5为平动自由度编号,u6~u25为转动自由度编号。
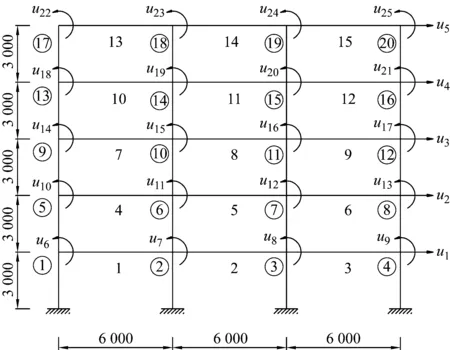
图1 五层三跨框架示意图
按照上述自由度的编号方式,式(1)可用分块矩阵的形式表示为
(2)
式中:φit、φi0分别表示第i阶振型平移分量和振型转角分量,Ktt、Kt0、K0t、K00和Mtt为对应的刚度分块矩阵和质量分块矩阵。取φit为对质量矩阵的标准化振型平移,即
(3)
式(2)可以表示为以下两个方程
(4)
K0tφit+K00φi0=0
(5)
由式(5)可得
(6)
将式(6)代入式(4)得
(7)
通常结构损伤造成结构刚度减小,不会引起结构质量变化。因此,式(7)对第s根杆件的线刚度is求偏导数得
(8)
式(8)两边前乘第r阶振型平移的转置,并利用振型对质量矩阵的正交性得
(9)
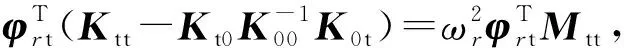
(10)
结构各阶振型平移为一组线性无关的向量,结构任一阶振型平移对构件线刚度求导后仍为向量,可表示为结构各阶振型平移的线性组合,即
(11)
将式(11)代入式(10)得
βr=
r≠i
(12)
Ktt、Kt0和K0t仅与柱的刚度有关,因此,当只有梁发生损伤时,有
(13)
(14)
(15)
将式(13)、(14)和(15)代入式(12)得
(16)
式(5)两边对is求偏导数得
(17)
式(6)两边对is求偏导数得
(18)
比较式(17)和式(18)得
(19)
将式(19)代入式(16)得
(20)
通过上述代换,可避免对逆矩阵求导。
当r=i时,有式(3)成立。式(3)两边对is求偏导数得
(21)
将式(11)代入式(21)得
βi=0
(22)
将式(20)和代入式(11)得
(23)
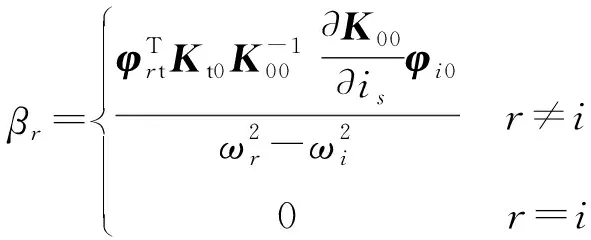
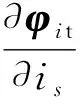
(24)
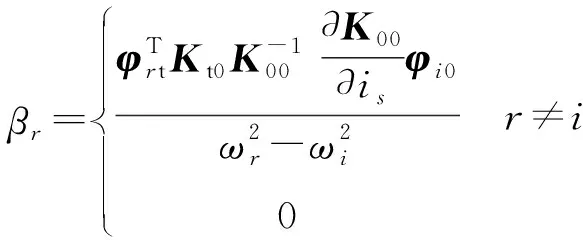

2 框架梁损伤检测方法
2.1 损伤位置检测方法
由式可见,结构以某阶振型振动时,与该阶振型对应的惯性力与弹性恢复力相互平衡。当某梁发生损伤时,该梁所在楼层的层间抗侧刚度减小。由于结构的质量不发生改变,忽略结构损伤造成结构频率的微小改变,则作用在各层的惯性力保持不变。因此,包含损伤梁的楼层层间振型位移增大,楼层层间振型位移的增大将导致损伤梁所在楼层梁柱节点转角增大。由于梁损伤削弱了梁对节点转动的约束能力,与损伤梁相连的梁柱节点比同层其余节点会发生更大的转角改变。因此,在单根梁发生损伤的情况下,可根据梁两端振型转角的改变判别损伤梁位置:当某梁的两端节点振型转角均发生显著改变时,则该梁为损伤梁。
当有多根梁发生损伤时,由于多损伤的相互影响,上述单损伤的损伤位置判别方法有可能发生漏判。基于敏感性分析结果,采用迭代算法可消除多损伤的相互影响,进行损伤梁的位置判别。

(25)

(26)

(27)
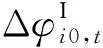
当多根梁发生损伤时,利用迭代算法消除多损伤的相互影响。第1步选出所有两端节点振型转角改变显著增大的梁,这些梁的编号用s1表示。第2步,利用式计算每一根所选出梁的损伤对其余梁柱节点的振型转角改变的影响,即
(28)

(29)
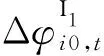
2.2 损伤程度检测方法
从损伤定位算法可以发现,通过迭代消除了多梁损伤的相互影响,迭代终止后损伤梁两端的振型转角改变仅仅由其自身的损伤造成,与其它梁的损伤无关。因此,梁的损伤程度可以用迭代终止后的修正节点振型转角改变来确定。
(30)
框架梁损伤识别的流程如图2所示。
3 数值算例
3.1 结构模型与损伤工况
以一五层三跨框架(见图1)为例验证所提出的框架梁损伤识别方法。框架各层层高和各跨跨度分别为3 m和6 m,框架梁的截面尺寸为0.2 m×0.5 m,框架柱的截面尺寸为0.5 m×0.5 m,图中梁下数字为梁编号,圆圈内数字为节点编号。每层的质量均为50 000 kg,梁、柱的弹性模量取3×104N/mm2。考虑三种损伤工况,工况1和工况2分别为不含噪声的单损伤和多损伤工况,工况3为在多损伤工况2的基础上添加了10%的高斯白噪声[16],以研究测试噪声对识别结果的影响,各工况如表1所示。

图2 框架梁损伤识别流程图
Fig.2 Flow chart of damage identification for frame structures
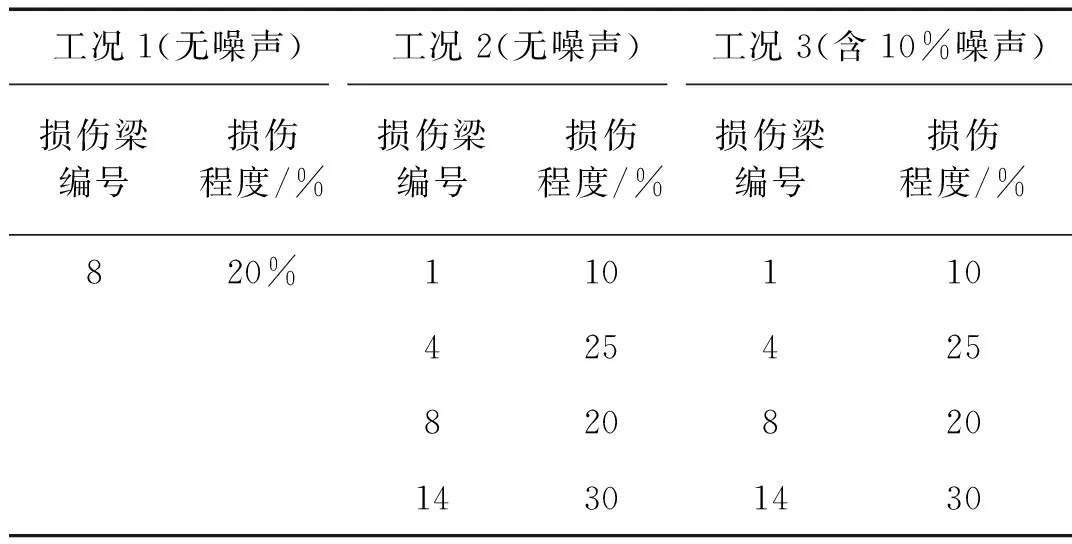
表1 损伤工况
3.2 损伤位置检测
由于在模态实验中低阶模态信息更易准确提取,因此仅采用一阶模态数据进行损伤识别。三种工况下损伤前后初始一阶振型转角改变如图3所示。
由图3(a)可见,损伤后节点10和节点11一阶振型转角显著增大,恰好为损伤梁8两端的节点。由图3(b)可见,梁4两端的5号和6号节点、梁8两端的10号和11号节点、梁14两端的18号和19号节点一阶振型转角显著增大,恰好梁4、梁8、梁14是损伤梁。但是,由于多损伤的影响,损伤梁1两端节点1和节点2的一阶振型转角改变并未显著增大,其值反而小于0。如果直接根据初始一阶振型转角改变显著大于0来判别损伤梁的位置,会漏判梁1的损伤。由于测试噪声的影响,图3(c)中各节点的一阶振型转角变化情况与图3(b)有些细微的差别,但总体变化情况一致。
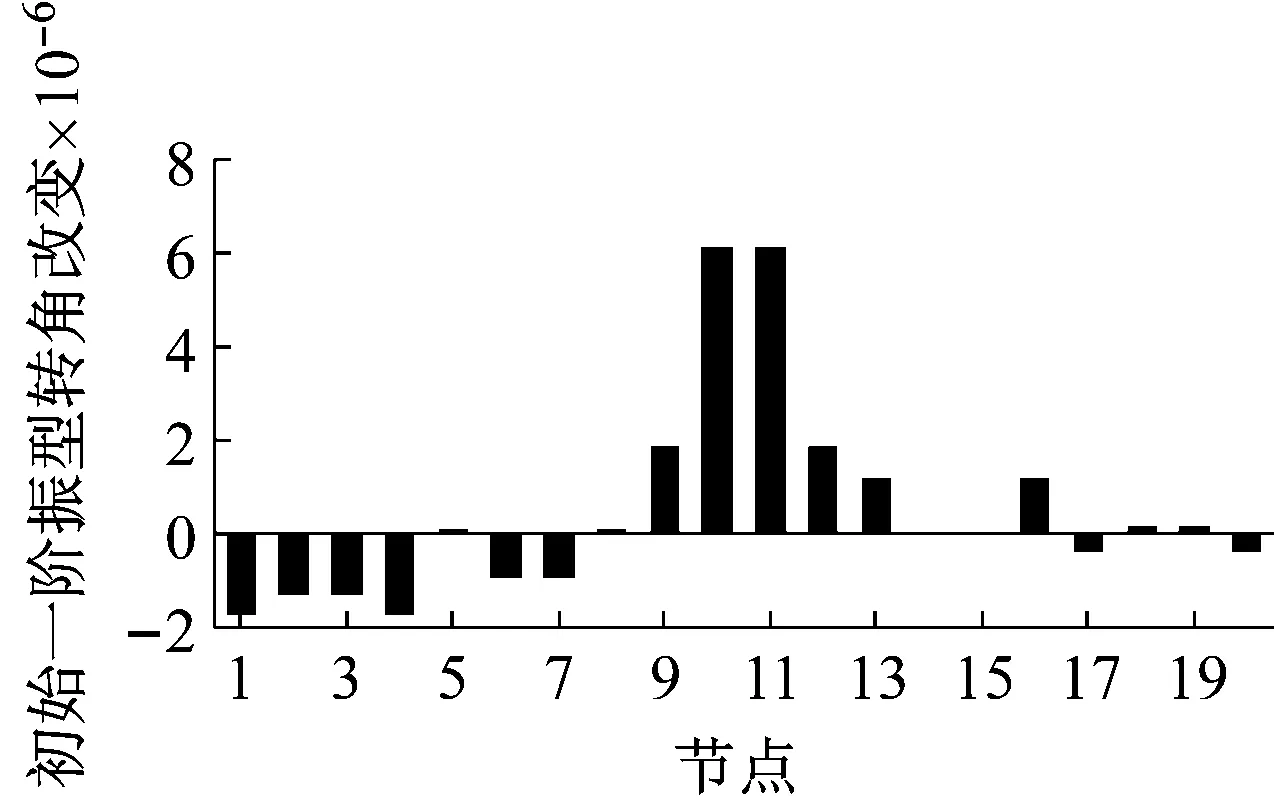
(a) 工况1
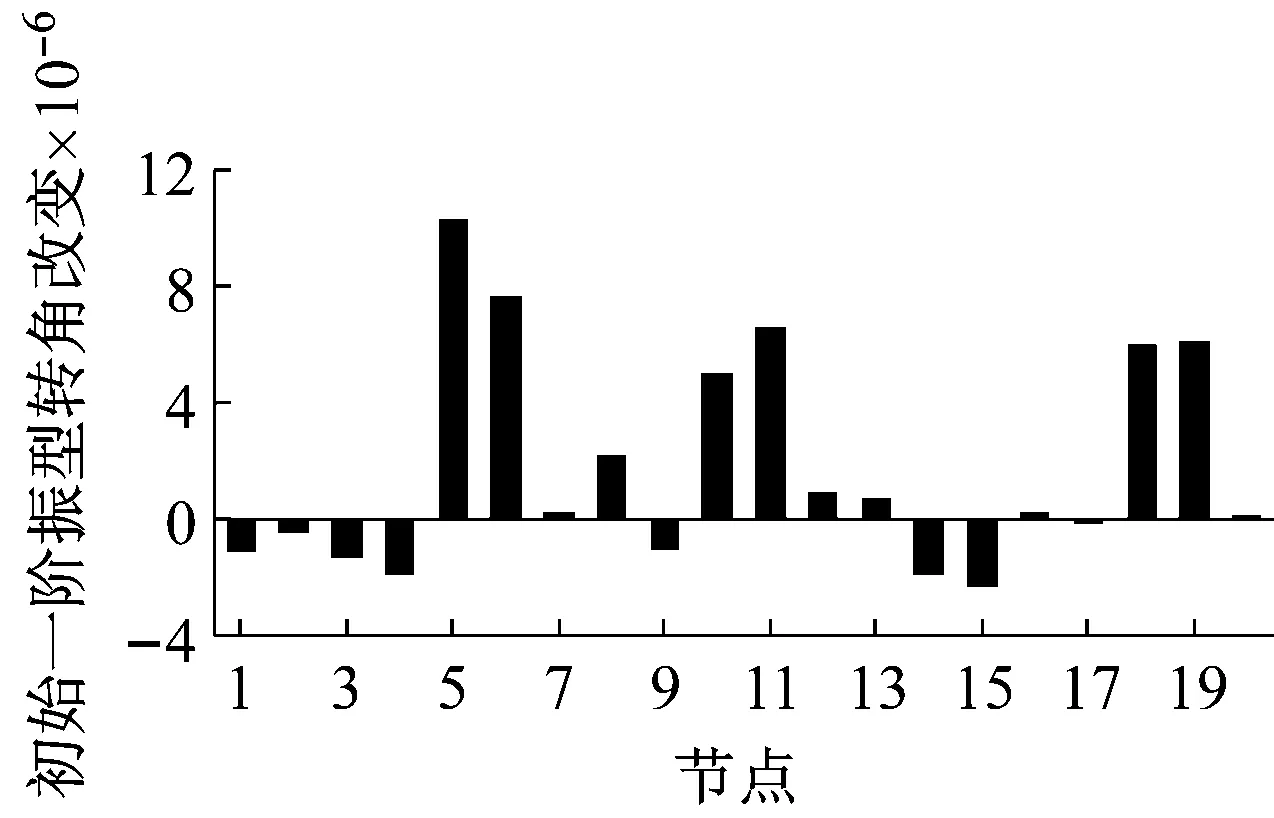
(b) 工况2
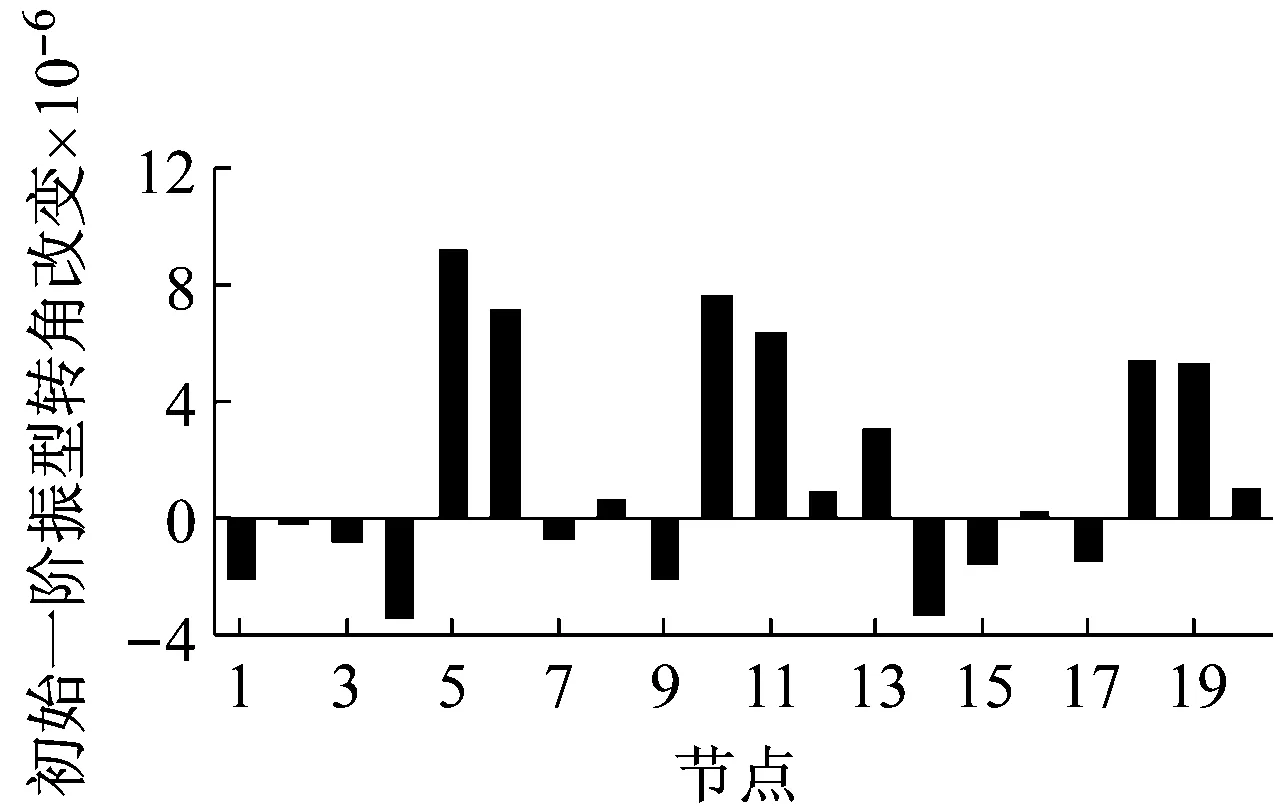
(c) 工况3
以节点初始一阶振型转角改变为基础,通过迭代计算来消除多损伤的相互影响,迭代过程如图4所示。由图4(a)可见,梁8两端节点10和11的一阶振型转角改变值保持不变(由于节点10和11的一阶振型转角改变值相等,图中二者的曲线重合),其余所有梁柱节点一阶振型转角改变值趋近于0,因此可判断梁8发生了损伤。由于仅梁8发生损伤,为单损伤工况,不存在多损伤的相互影响,因此仅通过一次迭代就能够收敛。由图4(b)可见,通过迭代,梁1两端的节点1和2、梁4两端的节点5和6、梁8两端的节点10和11、梁14两端的节点18和19的一阶振型转角改变值趋于某一固定的正值,其余所有节点一阶振型转角改变值趋近于0,因此,可判断工况2中梁1、4、8和14发生了损伤。对于中间跨梁,如梁8,由于对称性,迭代终止后的两端节点一阶振型转角改变值基本相等;对于边跨梁,如梁4,迭代终止后的两端节点一阶振型转角改变值不相等。特别注意经过迭代,梁1两端节点1和2的一阶振型转角改变值从负值变为了正值,从而能够判断出梁1发生了损伤。由于多损伤的影响,需要迭代3步后才能收敛。由于测试噪声的影响,图4(c)中未损伤梁端振型转角迭代终止值未趋近于0,而为一些较小值,工况3迭代终止后的节点一阶振型转角改变如图5所示。由图可见,根据同一梁端节点转角同时显著增大的梁为损伤梁的判别准则,仍可准确判别梁1、4、8和14发生了损伤。
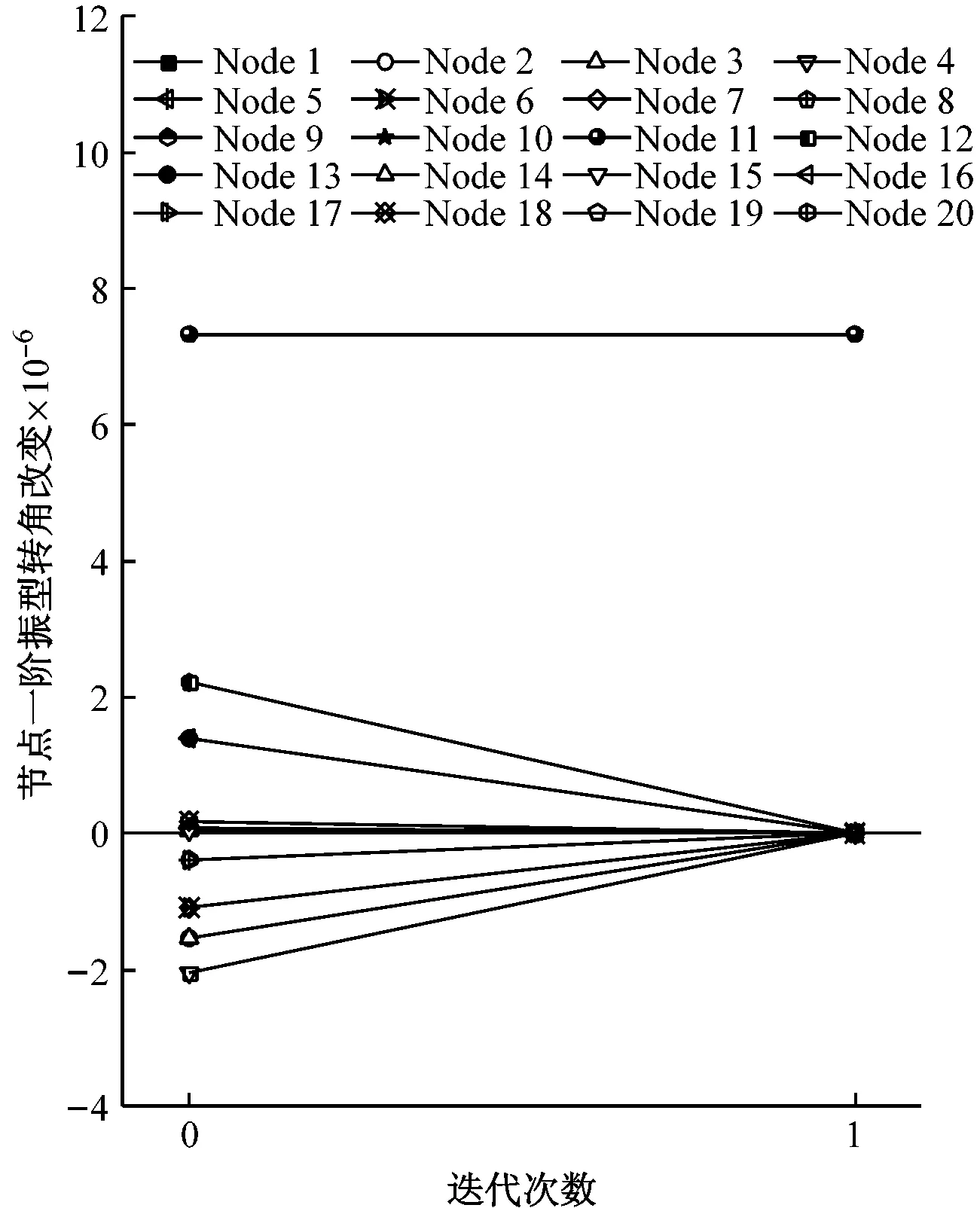
(a) 工况1
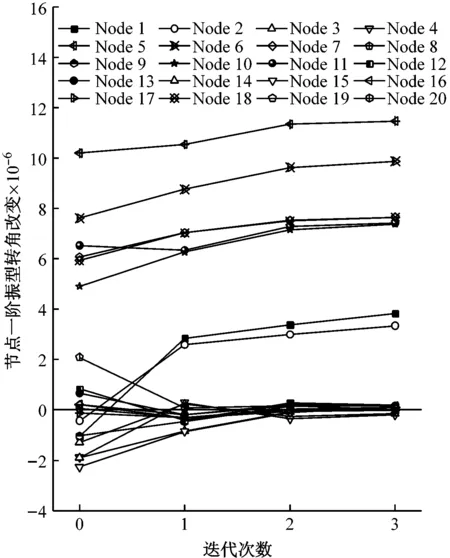
(b) 工况2
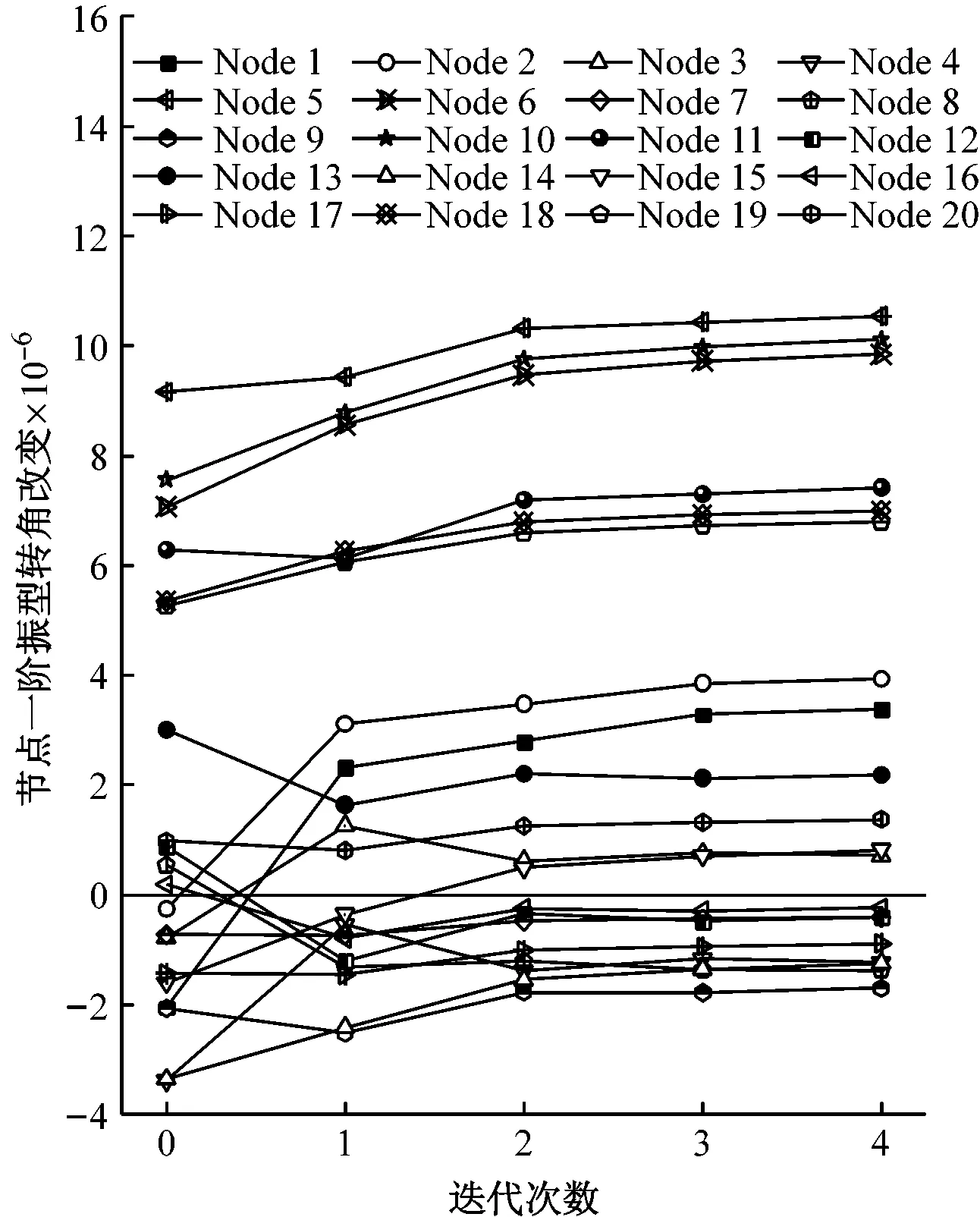
(c) 工况3
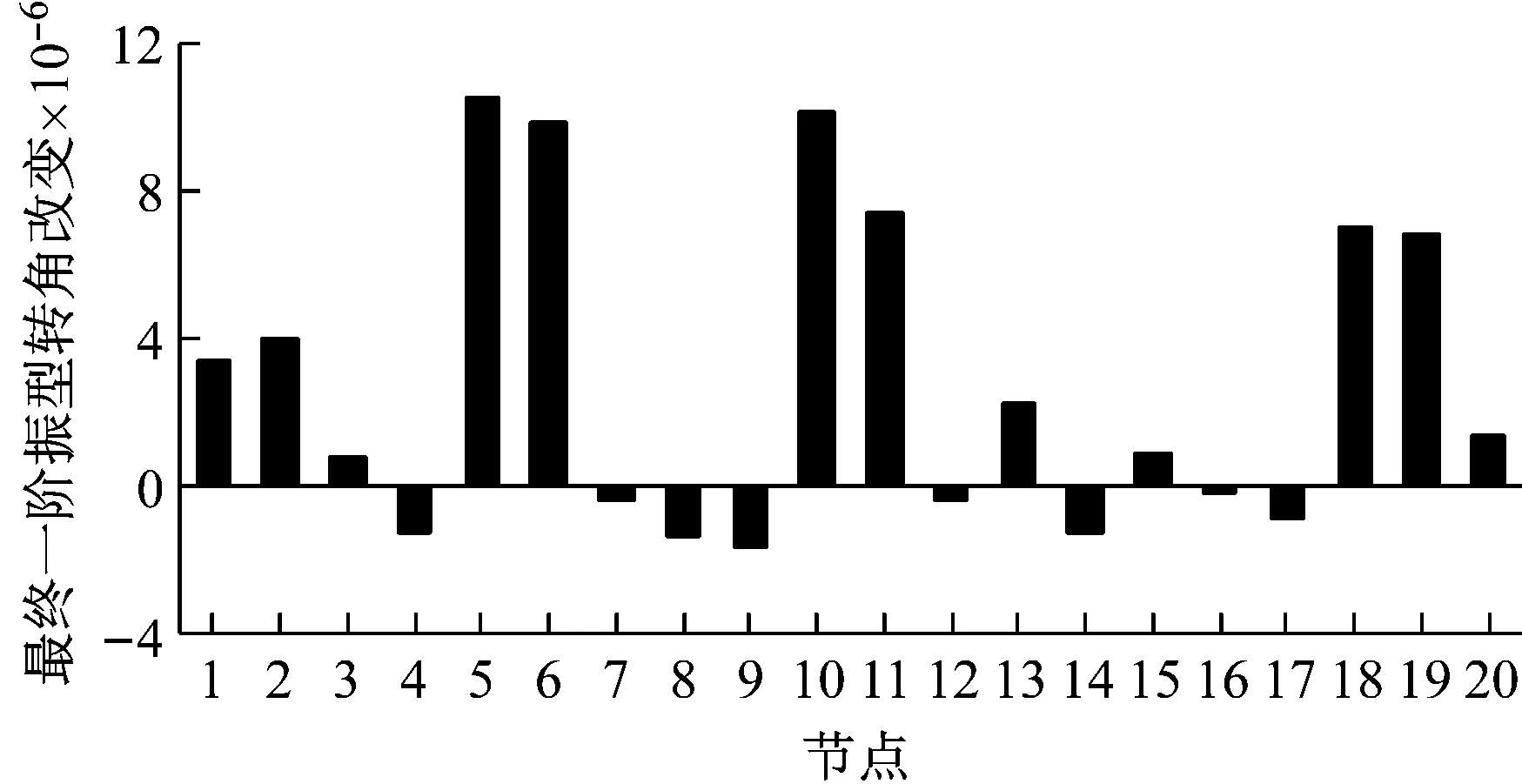
图5 工况3节点最终一阶振型转角改变
Fig.5 The final changes in the first mode shape rotational angles of beam-column nodes in case 3
3.3 损伤程度检测
根据损伤梁的位置判别结果,假设梁1、4、8、14分别发生5%、10%、……、40%的损伤,计算得到各损伤程度下损伤梁端节点的一阶振型转角改变,如表2所示。然后,根据迭代终止后的损伤梁端节点修正一阶振型转角改变值的大小,对应表2中的数据按照式计算各梁的损伤程度。当梁两端节点的一阶振型转角改变值不相等时,取平均后再插值。损伤程度识别结果如图6所示。由图6(a)和(b)可见,单损伤工况和多损伤工况下损伤梁的损伤程度均得到了准确的识别。由图6(c)可见,噪声给损伤程度的识别结果造成一定的误差,但误差较小,在可接受的范围,本方法具有较强的抗噪能力。
表2损伤梁不同程度单损伤工况下梁端一阶振型转角改变值(×10-6)
Tab.2Thechangesinthefirstmodeshaperotationalanglesofbeam-columnnodesofdamagedbeamsindifferentsingledamagecases
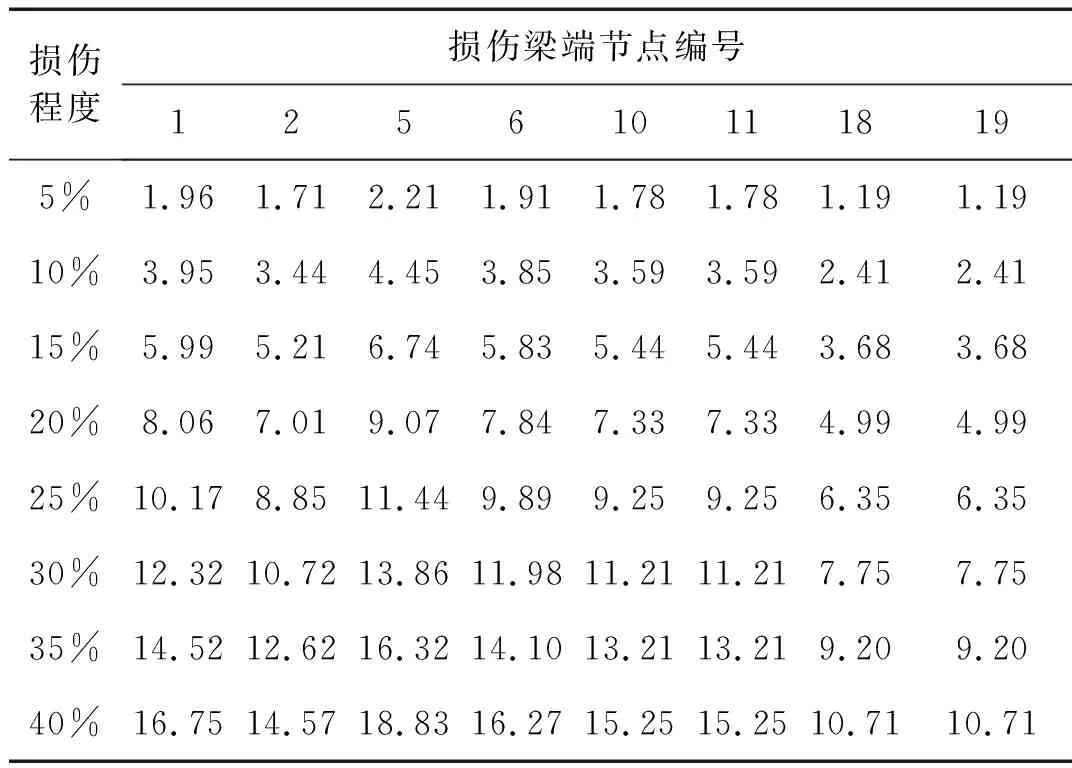
损伤程度损伤梁端节点编号1256101118195%1.961.712.211.911.781.781.191.1910%3.953.444.453.853.593.592.412.4115%5.995.216.745.835.445.443.683.6820%8.067.019.077.847.337.334.994.9925%10.178.8511.449.899.259.256.356.3530%12.3210.7213.8611.9811.2111.217.757.7535%14.5212.6216.3214.1013.2113.219.209.2040%16.7514.5718.8316.2715.2515.2510.7110.71
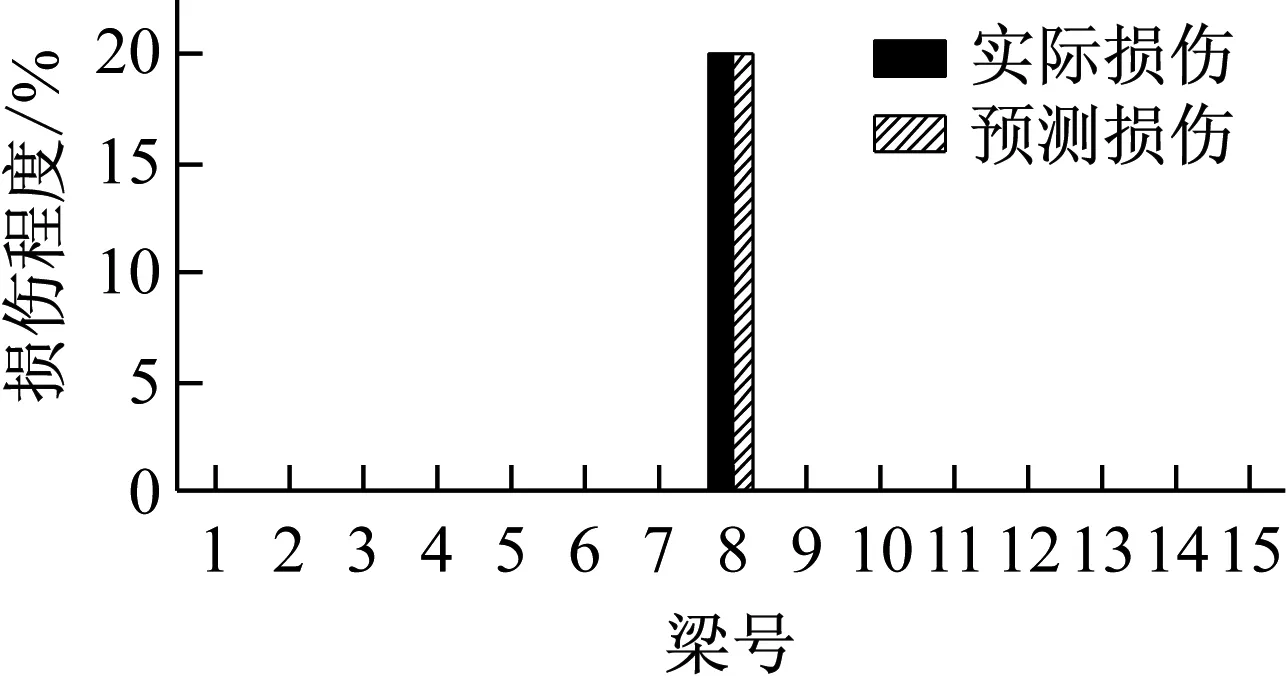
(a) 工况1

(b) 工况2

(c) 工况3
4 结 论
在梁柱节点振型转角敏感性分析的基础上,通过迭代计算能够准确识别框架结构梁的损伤位置和损伤程度。相对于高阶模态数据,低阶模态数据能够更加容易准确地获得。本方法可仅利用结构的第一阶模态数据进行损伤识别,因此更加易于在实际工程中得到应用。
