动环补偿型液膜密封三自由度动力学响应特性分析

2019-01-23李勇凡郝木明孙鑫晖李振涛王赟磊曹恒超

振动与冲击 2019年1期

李勇凡，郝木明，孙鑫晖，李振涛，王赟磊，曹恒超

(中国石油大学(华东) 密封技术研究所，山东青岛 266580)

液膜润滑非接触式机械密封(简称“液膜密封”)因其具有可实现工艺介质零泄漏或零逸出、改善密封摩擦副润滑状态和提高系统稳定性等显著特点，在工程中得到广泛应用，螺旋槽液膜密封为典型代表[1-2]。依据弹性元件是否随轴旋转可将机械密封分为旋转式和静止式两类，旋转式机械密封的动环为补偿环(将其称为“动环补偿型密封”)，适用于低速场合(端面线速度小于20～30 m/s)[3]，即常见的液膜密封运行工况。

实际应用中受加工精度和装配精度限制，机械密封环普遍存在角偏差，且存在转轴振动[4]，这两者直接影响了液膜密封的动态追随性[5]，因此有必要对密封的动力学响应特性加以研究。对动环补偿型密封动力学特性的研究起始于20世纪80年代，Green[6-7]建立了动环补偿型密封的运动方程，求解了非接触式锥面密封的线性化动力学系数以及稳态响应，指出该特性是由静环固定角偏差和动环初始角偏差引起的。在Green研究的基础上，An等[8]通过实验研究了动环补偿型密封的动力学特性，测得了不同端面锥度下的动环响应。Wileman等[9-11]对双动环补偿型机械密封的动力学系数及稳态响应特性开展了研究，并考虑了偏心因素。王之栎等[12]分析了瞬态扰动力作用下反转轴间气膜密封前密封跑道和主密封环的振动过程，并研究了系统质量、压力等因素对振动的影响。Liu等[13]建立了三自由度模型，研究了波-锥-坝机械密封的动力学性能。Blasiak等[14]理论研究了四种端面型式结构下，静环补偿型气体端面密封的动力学特性，分析了转速、造型参数、支撑系统刚度和阻尼对膜厚及相对角偏差响应的影响。陈源等以高参数干气密封为研究对象，对比了动环挠性安装、静环挠性安装及动静环均挠性安装条件下的密封的动态追随性。杨文静等[15]分析了螺旋槽液膜密封的动态特性，同时考虑了端面锥度和波度，但未求解密封的动力学响应特性。

综上所述，虽然国内外对机械密封动态特性的研究较为广泛，但针对液膜密封动力学响应特性的研究仍十分匮乏。因此，本文选择工程中常见的动环补偿型液膜密封为研究对象，研究动环初始角偏差、静环固定角偏差[16]、转轴轴向振动对其补偿环轴向及角向响应的影响规律。

1 计算模型

1.1 动环补偿型液膜密封结构

图1为动环补偿型液膜密封的剖视图，静环固装于机壳上、为非补偿环，其端面存在一定的固定角偏差γs，动环挠性安装于轴或轴套上、为补偿环，其端面存在一定的角偏差γr。图2为端面槽型结构，外径处开有螺旋槽，动环旋转时，液体在黏性剪切力作用下进入动压槽，并在槽根处形成高压区，密封端面在流体动压力作用下保持非接触运行。

1-静环; 2-动环; 3-O形圈; 4-弹簧; 5-传动销; 6-动环座;ω-角速度;γs-静环固定角偏差;γr-动环角偏差 I-介质侧; II-隔离液侧

图1 动环补偿型液膜密封结构

Fig.1 Structure of liquid film seal with flexibly mounted rotor

1.2 运动学模型

图3为动环补偿型液膜密封运动学模型，为了完整地描述密封运转过程中补偿环(动环)的位置及运动状态，共引入了四套坐标系：

ri-端面内半径; ro-端面外半径; rg-槽根半径

(1) 惯性参考坐标系XYZ,为空间固定坐标系。

(2) 旋转参考坐标系ξηζ,以角速度ω随轴旋转，ζ向与Z向一致。

(3) 动环参考坐标系xryrzr,xr轴位于ξη平面内，yr轴指向动环平面与ξη平面相距最远的方向，动环绕zr轴旋转；ψr为动环角偏差相位角，ψri为动环初始角偏差相位角。

(4) 静环参考坐标系xsyszs,xs轴与ξη平面平行，ys轴指向静环平面与ξη平面相距最近的方向；γs为静环固定角偏差，ψs为静环固定角偏差相位角。

图3 动环补偿型液膜密封运动学模型

1.3 补偿环力学模型

对补偿环的受力分析如图4所示，由图可知，补偿环的运动情况包括轴向移动、角向摆动以及随轴转动，补偿环受到的作用力则包括闭合力(Fsp和Fs)、开启力(Ff)、O形圈对补偿环产生的作用力、液膜对补偿环的倾覆力矩Mf。

Kax-O形圈轴向刚度;Dax-O形圈轴向阻尼;Kan-O形圈角向刚度;Dan-O形圈角向阻尼;Mf-液膜对补偿环的倾覆力矩;Ff-液膜承载力;Fs-介质力;Fsp-弹簧力;ho-中心位移

图4 补偿环受力分析

Fig.4 Force analysis of compensated ring

1.4 数学模型

对端面间液膜作以下假设：① 为牛顿流体层流运动；② 密度不变；③ 黏度不变；④ 不考虑离心力和惯性力的影响。则柱坐标系下计入挤压效应项雷诺方程为

(1)

式中：h为液膜厚度，m；μ为流体动力黏度，Pa·s；p为液膜压力，Pa。

密封环的角偏差较小，通常小于1 mrad，因此可以将其作为矢量处理，向X轴和Y轴分解，图3中动环角偏差γr绕X轴的分量为γrX=γr·cosψr，绕Y轴的分量为γrY=γr·sinψr；引入呈正弦波动的轴向激励项Ast·sin(ωt)，Ast为轴向激励振幅，则膜厚函数为

h(r,θ)=Ast·sin (ωt)+ho+〈hg〉-r·sin(θ-ψs)·γs+r·sinθ·γrX-r·cosθ·γrY

(2)

补偿环轴向及角向动力学方程组如式(3)～(5)所示

(3)

(4)

(5)

液膜承载力由下式计算

(6)

X向及Y向倾覆力矩分别计算如下

(7a)

(7b)

2 动力学响应特性的数值求解

通过数值迭代方法实现计入挤压效应项雷诺方程与动力学方程组的联立求解，从而得到液膜密封补偿环膜厚及角偏差的响应特性。

2.1 液膜控制方程离散

采用有限差分法离散雷诺方程，选用向后Euler法离散其中的挤压效应项[17]。由于考虑角偏差，求解区域选为全环。网格由沿r方向和θ方向分布的线束构成，r方向边长为Δr，θ方向弧段圆心角为Δθ，某节点P及其相邻节点E、S、W、N，如图5所示。

图5 网格节点及相关符号

离散化雷诺方程如下式所示

AP·PP+AE·PE+AS·PS+AW·PW+

AN·PN=AH+AT

(8)

式中：

2.2 求解流程

设定计算总时长T和时间微元Δt，在每个Δt内联立求解式(2)～(8)，得到液膜密封动力学响应特性。求解流程如图6所示。

步骤1输入液膜密封的结构参数和操作参数(如表1所示)，设置初始动力学参数(如表2所示)；

步骤2确定计算域并划分网格，r的范围为ri≤r≤ro，θ的范围为0≤θ≤2π；

步骤3设置边界条件并为计算域赋初值，r=ri时，压力为pi，r=ro时，压力为po；

步骤4设置误差限ε=10-5，采用逐次超松弛法(Successive Over-Relaxation Method，SOR法)迭代求解计算域压力场，超松弛因子β=1.97；

步骤5求解液膜承载力及倾覆力矩；

步骤6将液膜承载力、倾覆力矩和动力学参数代入动力学方程组，求解该时刻动力学参数；

步骤7判断是否达到计算时长T，若未达到，则将本次求得的压力场及动力学参数代回步骤4继续求解，若已达到，则输出数据，程序运行结束。

图6 动力学响应特性求解流程图

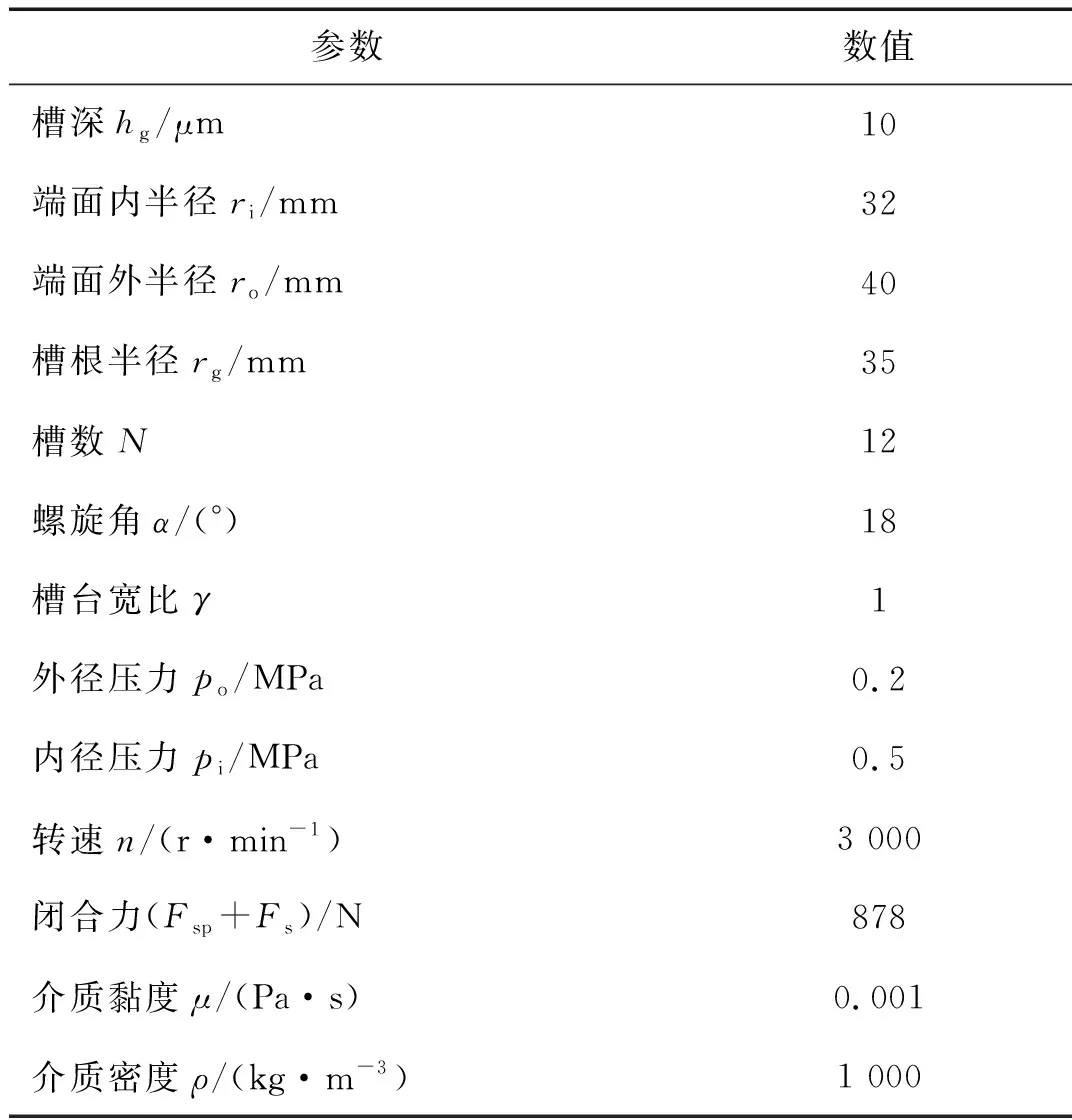
参数数值槽深hg/μm10端面内半径ri/mm32端面外半径ro/mm40槽根半径rg/mm35槽数N12螺旋角α/(°)18槽台宽比γ1外径压力po/MPa0.2内径压力pi/MPa0.5转速n/(r·min-1)3 000闭合力(Fsp+Fs)/N878介质黏度μ/(Pa·s)0.001介质密度ρ/(kg·m-3)1 000

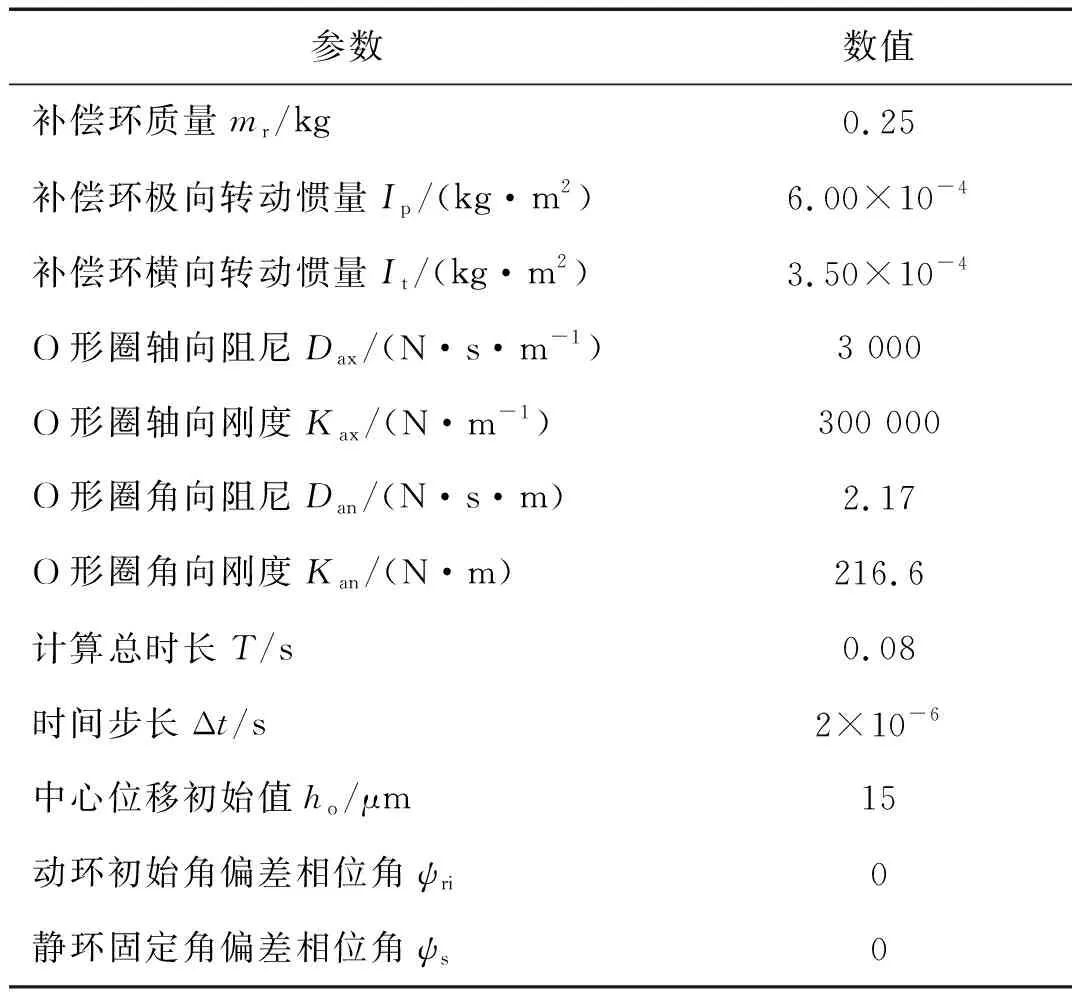
表2 液膜密封动力学参数

3 结果分析与讨论

基于表1、表2所示参数，选取不同轴向激励振幅、静环固定角偏差及动环初始角偏差，求解补偿环的轴向及角向响应特性。

3.1 各因素影响性对比

为对比各因素的影响性，综合比较表3所示4种工况下补偿环的响应特性。

表3 A1～A4的工况参数

图7为四种工况下的中心位移响应曲线，由图可知，A1～A3工况下，ho均由初始值平稳过渡至稳定值，分别为8.315 μm、8.318 μm、8.324 μm；A4工况下，ho由初始值平稳过渡至平衡位置附近后呈正弦波动，平衡值为8.315 μm、与A1稳定值一致，周期为0.02 s、与激励项周期一致，相位较激励项滞后π，但振幅远小于激励项振幅(50 μm)，仅为1.585 μm。

图7 中心位移响应曲线

上述结果表明，静环固定角偏差及动环初始角偏差对中心位移平衡位置的影响较小，与A1相比，A2和A3的稳定值仅分别增大了0.003 μm和0.009 μm；轴向激励对中心位移响应的影响明显，使补偿环发生一定振幅的正弦波动。

图8为四种工况下补偿环X向角偏差响应曲线，由图可知，A2工况下，γrX由初始位置平稳过渡至静环固定角偏差位置处(0.25 mrad)；A3工况下，γrX呈正弦波动，波动幅度为0.008 2 mrad，平衡位置为0 mrad；A4工况下，γrX未发生波动，与A1工况的响应线重合。

图8 X向角偏差响应曲线

图9为四种工况下补偿环Y向角偏差响应曲线，由图可知，A2工况下，γrY由初始位置经波动后过渡至一稳定值，波动峰值为0.020 2 mrad，稳定值为0.004 4 mrad；A3工况下，γrY呈正弦波动，波动幅度为0.008 2 mrad，平衡位置为0 mrad；A4工况下，γrY未发生波动，与A1工况的响应线重合。

图9 Y向角偏差响应曲线

A2工况下，γrY的响应现象解释如下：γs的相位角ψs为0，因此，端面相对旋转时Y轴两侧的流体膜分别呈收敛型和发散型，由此产生的流体动压差使补偿环发生Y向转动，形成波动峰值；随着γrX逐渐接近γs，上述流体动压差亦随之减小，γrY恢复至初始位置附近；因动环具有一定的极向转动惯量，γrY的稳定值相对初始位置偏离0.004 4 mrad。

A3工况下，γrX及γrY的响应现象解释如下：因动环具有一定的初始角偏差γri，当其偏离该位置时，辅助密封圈及弹性元件将对动环本身产生了一定的倾覆力矩，该力矩造成了动环的角振动，因此γrY的波动幅值与γrX相同，而γrY的相位较γrX滞后π/2。

A4工况下，γrX及γrY均未发生响应(同A1工况)，说明轴向激励对补偿环角向响应无影响。

图10为四种工况下补偿环角偏差轨迹线，由图可知，A2的角偏差轨迹线为抛物线状，A3的角偏差轨迹线为圆形，而A1、A4工况的轨迹一直位于原点。

图10 补偿环角偏差轨迹线(1)

3.2 轴向激励对轴向响应特性的影响

图11为轴向激励振幅对中心位移响应的影响。图11(a)为ho响应曲线，不同Ast条件下曲线趋势一致，均由初始值平稳过渡至平衡位置附近后呈正弦波动，平衡值均为8.315 μm，且各曲线相位一致；由图11(b)可知，波动幅度Δho随Ast的增大呈线性增大的变化趋势，Δho约为Ast的3.16%。上述结果表明液膜能够有效抵抗轴向激励，保持非接触运行状态。

(a) ho-t

(b) Δho-Ast

3.3 静环固定角偏差对响应特性的影响

图12为静环固定角偏差对中心位移响应的影响。图12(a)为ho响应曲线，不同γs条件下曲线趋势一致，均由初始位置平稳过渡至稳定值，各稳定值相差较小但仍呈现明显规律性，由图12(b)可知，hos随γs的增大而增大，且变化率也逐渐增大，表明随静环固定角偏差的增大，该值对补偿环轴向响应的影响越发凸显。

图13为静环固定角偏差对X向角偏差响应的影响，由图可知，不同γs条件下，γrX均由初始位置平稳过渡至γs值，表明液膜密封补偿环对非补偿环保持了良好的追随性。

图14为静环固定角偏差对Y向角偏差响应的影响。图14(a)为γrY的响应曲线，由图可知，不同γs条件下γrY均先发生波动后过渡至一稳定值；由图14(b)可知，γrY的波动峰值和稳定值均随γs的增大呈线性增大的变化趋势，但前者的数值和增长率均大于后者。这是因为γs增大造成Y轴两侧的流体动压差增大，进而造成响应初始阶段的波动峰值随之增大；而γs越大(即γrX越大)，动环极向转动惯量造成的Y向角偏差也随之增大。上述现象表明，静环X向角偏差会造成动环Y向角偏差相对于平衡位置的偏离。

(a) ho-t

(b) hos-γs

图13 静环固定角偏差对X向角偏差响应的影响

图15为不同静环固定角偏差下的补偿环角偏差轨迹线，由图可知，γs增大时，轨迹线幅度明显增大。

3.4 动环初始角偏差对响应特性的影响

图16为动环初始角偏差对中心位移响应的影响。图16(a)为ho响应曲线，不同γri条件下曲线趋势一致，均由初始值平稳过渡至稳定值，各稳定值相差较小但仍呈现明显规律性，由图16(b)可知，hos随γri的增大而增大，且变化率也逐渐增大，表明随动环初始角偏差的增大，该值对补偿环轴向响应的影响越发凸显。

(a) γrY-t

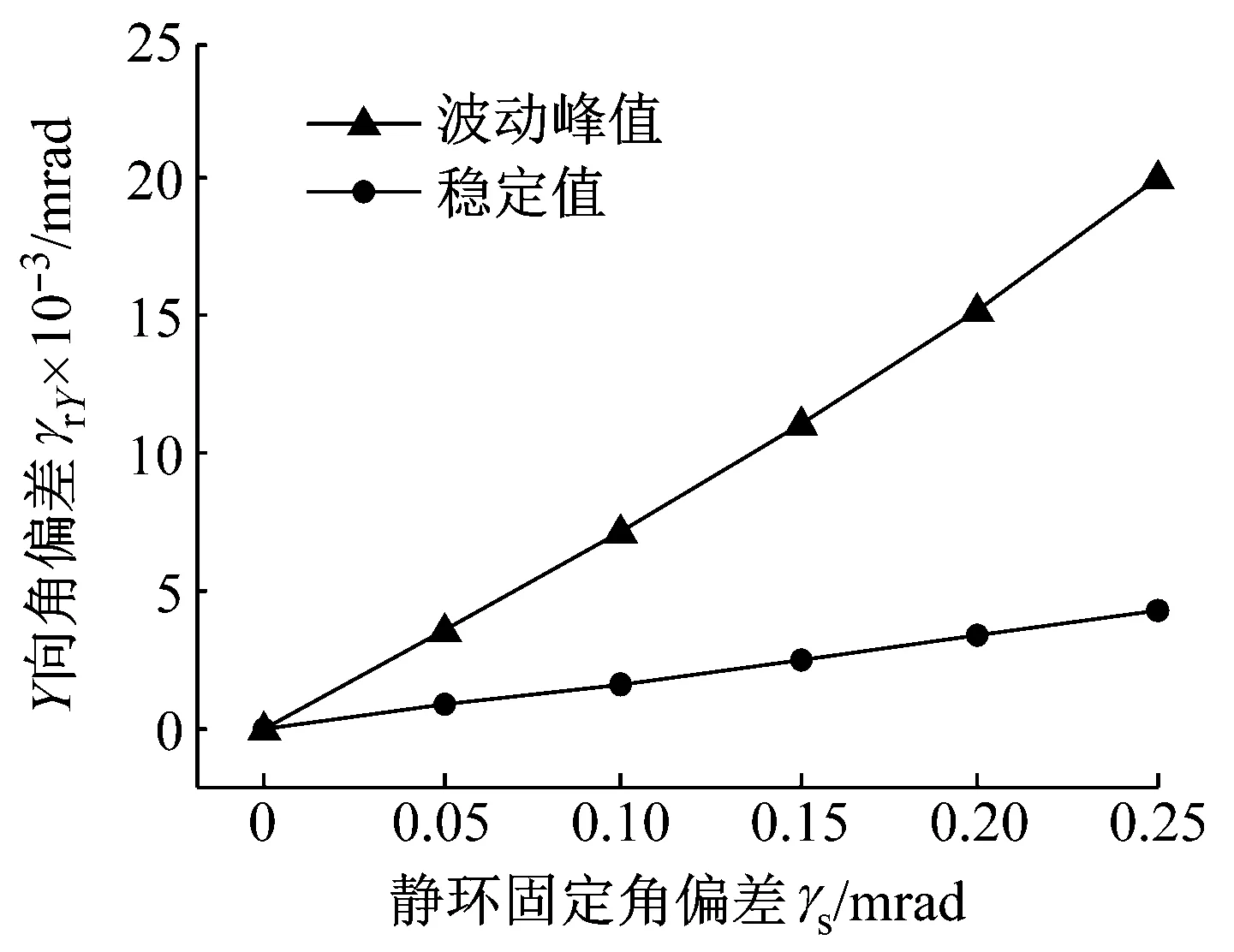
(b) γrY-γs

图15 补偿环角偏差轨迹线(2)

图17、18分别为动环初始角偏差对X向角偏差及Y向角偏差响应的影响。由图17(a)可知，不同γri条件下，γrX响应曲线相位一致，由初始值经过渡波动后，进入周期性波动阶段；由图18(a)可知，γrY响应曲线具有与γrX相同的规律，但过渡波峰、周期性波峰的相位均较γrX滞后π/2。综合比较图17(b)和图18(b)可知，不同γri条件下，动环X向及Y向角偏差的周期性波峰相同，即在密封稳定运行阶段动环会发生角振动，且周期性波峰随γri的增大呈线性增大的变化趋势，即动环的角振动幅度随γri的增大而增大，动环角偏差轨迹线如图19所示，稳定运行阶段该轨迹线呈圆形，即发生周期性角振动；过渡波峰也随γri的增大线性增大，但过渡波峰的值及增长率均大于周期性波峰，且γrX过渡波峰的值及增长率均大于γrY。