轨道不平顺激励下悬浮隧道车隧耦合振动响应分析

林 亨， 项贻强， 陈政阳， 杨 赢

(浙江大学 建筑工程学院， 杭州 310058)

悬浮隧道(Submerged Floating Tunnel, SFT)，又名阿基米德桥，是悬浮在水下一定深度的新型封闭式交通结构物[1]。悬浮隧道一般是由隧道管体，限制管体大位移的锚固装置和与两岸衔接的驳岸段组成。这种结构能够适应跨度较长、深度较深的海峡、湖泊、河流等水域，且在改善交通状况的同时，对周边环境的影响小。与传统海底隧道和沉管隧道相比，悬浮隧道与陆地连接的过渡段坡度要小很多，具有工程造价低的优势。因此，悬浮隧道被视为21世纪最具竞争力的跨江海域交通方案，得到国内外专家和学者的关注[2]。

相比其他结构，悬浮隧道依靠锚固在河床上锚索的张力来平衡自身重力与浮力的差值，在运营过程中常年受到水下洋流和车辆荷载的作用，运营的环境十分复杂。Remseth等[3]基于Navier-Stockes方程，建立考虑流体与固体相互作用的有限元模型，分析讨论了悬浮隧道随机动力响应。麦继婷等[4]采用空间梁系有限单元模型，考虑波流与悬浮隧道之间的相互作用，讨论结构放置深度、波浪入射方向及隧道断面形式等因素的影响。Sato等[5]认为相对刚度在小于一定范围的情况下，可以将等间距锚索支撑的悬浮隧道等效为作用在弹性地基上的梁，并在此基础上推导结构的控制方程。葛斐等[6]利用Hamilton原理推导得到了悬浮隧道管段和锚索的运动控制方程，并采用Airy线性波和Morison方程计算波浪力，分析了波浪场中悬浮隧道的动力响应。晁春峰等[7]以千岛湖悬浮隧道锚索为原型，对悬浮隧道锚索在均匀流作用下的涡激振动特性进行了试验研究。此类研究，加深了人们对这种新型结构受力特性的认识，为后期设计建造悬浮隧道提供理论支撑和依据。

随着高铁和轻轨的兴起，车辆荷载作用下结构的动力响应问题逐步受到人们的重视，对于悬浮隧道也不例外。Tariverdilo等[8]将移动车辆等效为移动常荷载，考虑流体附加的惯性效应分析了悬浮隧道的动力响应。董满生等[9]将悬浮隧道简化为两端有阻尼的弹性支撑梁，分析考虑了等间距移动荷载对悬浮隧道管体的位移响应。虽然移动荷载能够近似反映行驶车辆的移动特性，但却在分析过程中忽略了车辆与隧道在行驶过程中的耦合作用。基于此，本文拟将行驶车辆和悬浮隧道分别抽象为弹簧-质量车和离散弹性支撑梁，并结合Morison方程考虑流体附加惯性效应和阻尼效应，建立悬浮隧道车隧耦合振动控制方程，基于MATLAB采用四阶龙格-库塔法对悬浮隧道在轨道不平顺激励下的车隧耦合振动进行分析，并讨论流体环境、轨道不平顺、锚索刚度、行驶速度等因素对悬浮隧道动力响应的影响。

1 理论分析模型

对于悬浮隧道而言，一般是由多节标准隧道管体、沿中轴线对称布置的锚索张力腿、管节连接装置、锚固装置等部分组成，锚索之间的间距分别为hi(i=1,2,…,Ns)，如图1(a)所示。其中，锚索张力腿因管体浮力始终处于张紧状态，且在一般静水情况下，张力腿上水平向力通过两侧对称的锚索分力自平衡抵消，故i位置处张力腿提供的竖向刚度可表示为Ki(i=1,2,…,Ns)，如图1(b)所示。

为了进一步研究车辆荷载作用下悬浮隧道的动力响应，做以下假定:① 不考虑横向波流作用，故在静水环境中隧道管体仅受锚索张力腿竖向约束力的作用；② 隧道两端与海岸连接，近似简化为简支边界条件，同时，忽略不同管节之间连接构造，将悬浮隧道整体视为Euler-Bernoulli梁；③ 为分析车隧耦合对悬浮隧道动力响应的影响，将行驶车辆简化为单自由度的弹簧-质量车，且车辆在行驶过程中不与轨道发生分离。

(a) 模型简化图

(b) 模型横断面

于是，可得到如图2所示的简化分析系统模型。

图2 简化分析模型

参照桥梁在弹簧-质量车荷载作用下的振动控制方程[10]，悬浮隧道的竖向动力平衡方程可以表示为式(1)所示

(1)

式中：EI为悬浮隧道的竖向弯曲刚度；w为悬浮隧道管体的竖向位移；ms为单位长度悬浮隧道的质量；cs为悬浮隧道的黏滞阻尼系数；δ为Dirac(狄拉克)函数；L为悬浮隧道总长度；Ki和wi分别为i位置锚索张力腿处的竖向刚度和竖向位移；mv为移动弹簧车质量；kv为移动弹簧车刚度；cv为移动弹簧车黏滞阻尼；v为移动弹簧车的速度；u为移动弹簧车相对其静平衡位置的竖向位移；R表示悬浮隧道轨道不平顺程度；fD为隧道管体竖向振动引起的流体对其单位长度的附加惯性力和阻尼力之和。

由Morison公式[11]，fD可表示为

(2)

式中：ρw为流体密度；D为管体直径；CD为拖曳力系数，Cm为附加质量系数，取CD=0.7，Cm=1.0[12]。

上述式(1)，可采用分离变量法[13]，将悬浮隧道位移w(z,t)表示为如下的形式

(3)

式中：φn(z)为悬浮隧道n阶的振型函数;qn(t)为悬浮隧道n阶的广义坐标。对结构两端简支约束中间离散支撑的悬浮隧道，其振型函数可近似的取为

(4)

用Galerkin法[14]将该偏微分方程转化为常微分方程组，整理得

(5)

通过上述变换得到的微分方程组，可见考虑车隧耦合的悬浮隧道结构体系是一个非线性变系数的耦合振动系统。在轨道不平顺激励下，弹簧质量车的竖向振动会引起悬浮隧道的竖向振动，同时结构振动将受到结构周围流体附加惯性力和流体阻尼力的影响，进一步影响移动弹簧车的竖向振动，悬浮隧道和弹簧质量车的竖向振动相互耦合。

2 轨道不平顺模型

轨道不平顺具有随机性，通常采用功率谱来描述轨道不平顺的统计特性。这里采用德国研究高速列车时选用的高、低干扰轨道谱模型，对车隧耦合的悬浮隧道动力系统进行振动分析[16]，即

(6)

式中:Ω为轨道不平顺的空间频率，单位为rad/m;Sv(Ω)为垂向不平顺功率谱密度，单位为m2/(rad/m);Av为粗糙度常数，高、低干扰轨道谱分别取15.86×10-7rad/m和5.293×10-7rad/m;Ωr,Ωc分别是截断频率，取值为0.020 6 rad/m和0.824 6 rad/m。

为了使研究的结果能从本质上反映出轨道不平顺和运行速度对系统的影响，把轨道谱从空间域转换到时间域。由于空间域与时间域谱密度函数对应谱带宽度内的均方值相等，则有Sv(Ω)dΩ=Sv(ω)dω。当车辆以速度v通过空间频率为Ω的一个波时，将产生频率为ω的一次激励，即ω=vΩ，于是可得

(7)

式中:Sv(ω)为时间域垂向不平顺功率谱密度；v为车辆运行速度，单位为m/s;ω为时间域频率，单位为rad/s；ωr，ωc为时间域截断频率，单位为rad/s。

国内外常用的轨道不平顺时域样本数值模拟方法有三角级数、白噪声滤波法、二次滤波法和逆Fourier变换法[17]。然而由于白噪声滤波法和二次滤波法模拟的样本作为激励输入时，其计算结果含有密集的高频成分，计算可信度较低，故采用三角级数法对轨道不平顺进行处理。假定轨道不平顺为0均值的平稳遍历高斯(Gaussian)过程，当上、下截止频率为ωu和ω1时，对于给定的功率谱密度Sx(ω)，用余弦级数对轨道不平顺进行模拟。

(8)

3 数值计算方法及算例

根据本文提出的理论及建立的方程，取结构前5阶振型函数进行考虑，整个求解的过程如图3所示。

图3 数值计算方法流程图

首先通过三角级数法，根据参数设定得到轨道不平顺时域样本序列，然后通过四阶-龙格库塔迭代计算得到t+Δt时刻结构和小车的位移响应，根据结构的速度响应可求得流体阻尼力。同时，根据车辆在行驶过程中不与轨道发生分离的位移协调假定，将轨道不平顺时域样本序列通过强制位移施加在车辆位移上，进而计算结构与车辆之间耦合作用力。整个过程是基于MATLAB编写有关程序实现的。

目前，世界范围内尚无一例建成的悬浮隧道工程实例，故文中悬浮隧道基本参数参考目前国内外拟建悬浮隧道的设计参数[18-19]，其中锚索等间距布置，布置形式相同，具体参数见表1。

基于文中所提出的弹簧质量车模型，假定其总质量为mv=1.2×105kg，弹簧车的刚度为kv=2.1×107N/m，弹簧车的阻尼为cv=85 000 N·s/m，移动速度为v=90 km/h。同时，三角级数法进行时域轨道不平顺的模拟，取轨道空间波长为0.01～250 m，分别拟合得到高、低干扰轨道不平顺样本序列，如图4所示。

表1 悬浮隧道基本参数取值

(a) 低干扰轨道不平顺

(b) 高干扰轨道不平顺

4 结果分析

4.1 流体环境和轨道不平顺的影响

在车辆行驶的路线段，由于轨道相对于理想的平滑轨道位置产生偏差，这种几何参数偏差称之为轨道不平顺，而轨道的高低不平顺是引起行驶车辆竖向振动的主要根源。又因为悬浮隧道常年在水下运营，结构振动时还将受到流体环境效应的影响。基于此，图5(a)和(b)分别给出考虑流体环境和不考虑流体环境情况下，弹簧-质量车以车速90 km/h行驶在不同轨道不平顺激励下悬浮隧道跨中位置位移时程曲线。可以发现，光滑轨道情况下，由于式(2)中流体惯性项的作用，流体环境中结构跨中位移值为7.28 mm，相比不考虑流体环境结构跨中位移值7.04 mm，增加了3.41%。同时，比较考虑流体环境与不考虑流体环境的结构跨中位移时程曲线发现，在轨道不平顺激励下，跨中位置的位移时程曲线在其对应的光滑轨道位移时程曲线基础上受迫振动。这说明车隧耦合作用将会对悬浮隧道动力行为产生影响，相比简化的移动荷载而言这种耦合振动效应不应该被忽视。

(a) 考虑流体环境

(b) 不考虑流体环境

同时，为了定量的分析流体环境对悬浮隧道在不同轨道不平顺激励下的车隧耦合振动的影响。分别将高、低干扰轨道不平顺激励下结构跨中位移值与光滑轨道情况下跨中位移值作差分析，得到高、低干扰轨道不平顺激励下跨中位置在不同时刻位移离差绝对值，并在此基础上作位移离差包络图曲线如图6所示。

由于轨道不平顺具有随机性，故将不同时刻的位移离差绝对值再作平均，通过该位置处的位移离差均值来定量描述该位置在车辆行驶过程中局部振动程度。由图6(a)和(b)可知，考虑流体环境悬浮隧道跨中在高、低干扰轨道不平顺激励下的位移离差均值分别为0.769 mm和0.347 mm，占其光滑轨道位移值10.92%和4.77%。而不考虑流体环境悬浮隧道跨中在高、低干扰轨道不平顺激励下位移离差均值分别为0.375 mm和0.222 mm，占其光滑位移值5.33%和3.15%。可以发现无论是否考虑流体环境，结构在低干扰轨道激励下的位移离差均值要小于高干扰轨道激励下的位移离差均值，考虑流体环境的位移离差均值要大于不考虑流体效应的位移离差均值。这说明，在高干扰轨道不平顺激励下，车辆行驶作用导致弹性支撑悬浮隧道更剧烈的振动，并且结构振动在流体环境中因为流体惯性力被进一步放大。

(a) 考虑流体环境

(b) 不考虑流体环境

4.2 结构锚索刚度的影响

锚索是悬浮隧道重要的支撑和限位结构，锚索截面、材料以及布置型式等因素通过影响锚索的支撑刚度对悬浮隧道振动特性产生重要的影响。常见的锚索布置形式有“M”型、“X”型和“川”型等[20]。静水环境中分别取锚索竖向等效刚度K为5×107N/m，8×107N/m和1×108N/m[21]，对悬浮隧道在高、低干扰轨道不平顺激励下跨中位置处的动力响应进行分析计算，得到计算结果如图7所示。由图7(a)和(b)可知，当K从5×107N/m增大至1×108N/m时，悬浮隧道在低干扰轨道不平顺激励下跨中最大位移值分别由10.58 mm减小至6.66 mm，两者相差-37.5%；而其在高干扰轨道不平顺激励下跨中最大位移值从12.03 mm减小至7.79 mm，两者相差-35.2%。对比发现，在相同干扰轨道不平顺激励下，锚索刚度较大的悬浮隧道，其跨中位移响应就越小。由此可见，锚索刚度对在轨道不平顺激励下的位移响应具有抑制作用。

(a) 低干扰轨道不平顺

(b) 高干扰轨道不平顺

与此同时，为了分析不同锚索刚度对悬浮隧道整体结构振动的影响，图8给出具有不同锚索刚度的悬浮隧道分别在高、低干扰轨道不平顺激励下，各位置处的位移离差均值的计算结果。通过图8(a)和(b)可见，位移离差均值沿着悬浮隧道长度方向起伏变化。受到边界和弹性支撑约束力影响，边界位置和锚索支撑处的位移离差均值在不同锚索刚度情况下差别不大，而在各跨中位置处的位移离差均值在不同锚索刚度情况下呈现一定的差异变化。计算结果能够验证本文所提出离散弹性支撑模型的准确性。

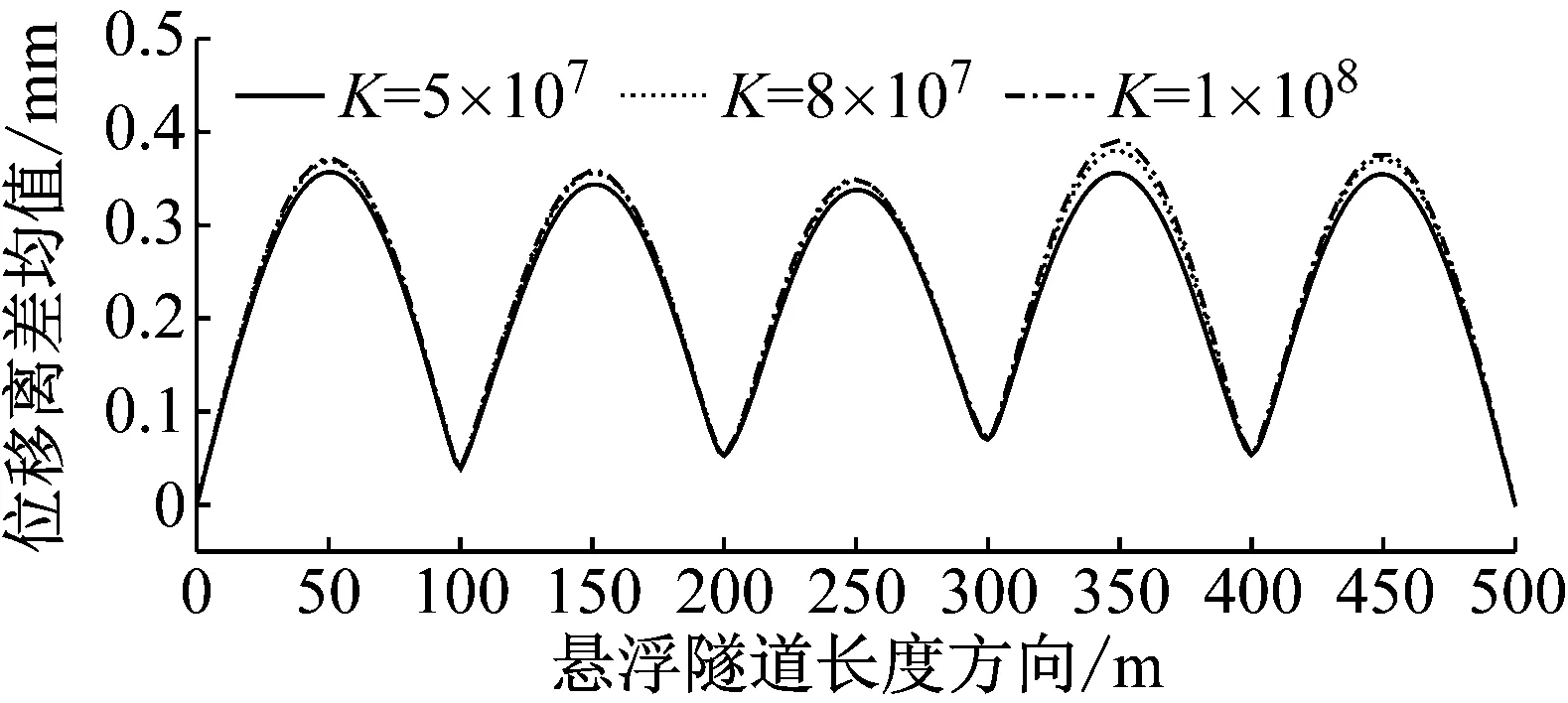
(a) 低干扰轨道不平顺

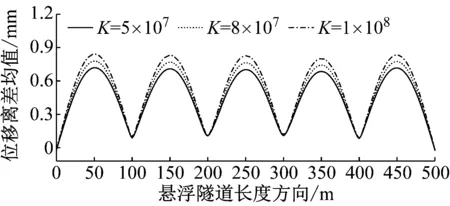
(b) 高干扰轨道不平顺

为分析在高、低不平顺激励下不同锚索刚度悬浮隧道动力行为的差异，比较不同工况下的位移离差均值可见，当K从5×107N/m增大至1×108N/m时，悬浮隧道沿隧道长度方向的整体位移离差均值均有所增加。同时，低干扰轨道不平顺激励下最大位移离差均值分别从0.356 mm增加至0.390 mm；而其在高干扰轨道不平顺激励下最大位移离差均值分别由0.726 mm增加至0.846 mm。相比而言，具有较大锚索刚度的结构整体位移离差均值增幅值要大于较小锚索刚度结构整体位移离差均值增幅值。结果表明，在轨道不平顺激励下，具有较大锚索刚度的悬浮隧道对轨道不平顺更敏感，局部振动更剧烈。

4.3 车辆行驶速度的影响

此外，车辆行驶的速度是影响悬浮隧道振动的另一个重要的影响因素。因此，对不同车辆行驶速度为30 km/h、60 km/h、90 km/h和120 km/h时，悬浮隧道在高、低干扰轨道不平顺激励下加速度响应进行计算，得到悬浮隧道跨中加速度响应包络图，如图9所示。由图9可知，低干扰轨道不平顺激励下，悬浮隧道结构跨中位置在不同行驶速度所对应的最大加速度幅值分别为163.42 mm/s2、126.44 mm/s2、167.73 mm/s2和145.27 mm/s2。而在高干扰轨道不平顺激励下，其所对应的最大加速度幅值分别为256.26 mm/s2、242.40 mm/s2、405.79 mm/s2和392.91 mm/s2。

(a) 低干扰轨道不平顺

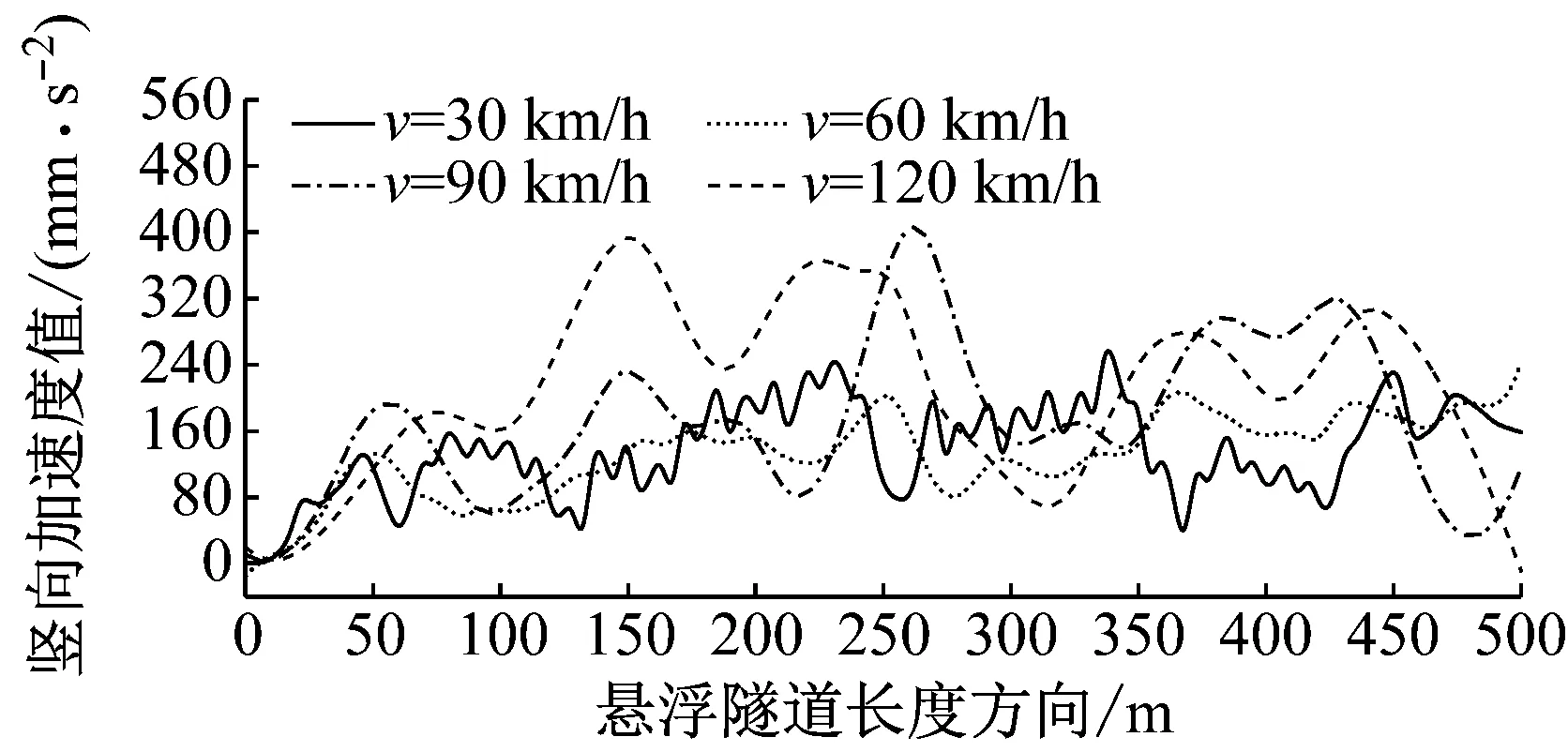
(b) 高干扰轨道不平顺

同时，对不同车辆行驶速度下车体加速度作频域分析，得到功率谱密度图，如图10所示。车辆的自振频率为2.11 Hz，车体加速度能够反映车辆振动的特性。比较车体加速度功率谱密度幅值，高干扰轨道不平顺激励下的加速度功率谱密度幅值要高于低干扰轨道不平顺激励下的功率谱密度幅值，且加速度功率谱密度幅值随着车速增加而增大。

总的来说，低干扰轨道不平顺激励情况下，耦合系统受车辆行驶速度的影响要低于高干扰轨道不平顺激励情况下。快速行驶车辆在高干扰轨道激励下向耦合系统输入更多的能量，使耦合系统发生更强烈的振动，故可通过控制车辆行驶轨道的平顺度以降低高速通行要求下产生的车隧耦合振动影响。

(a) 30 km/h

(b) 60 km/h

(c) 90 km/h

(d) 120 km/h

5 结 论

本文把车辆行驶在悬浮隧道的动力响应问题抽象为弹簧-质量车作用在两端简支的离散弹性支撑梁上的动力模型，并结合Morison方程考虑流体附加惯性效应和阻尼效应，建立了悬浮隧道车隧耦合振动的微分控制方程。通过四阶龙格-库塔法对悬浮隧道在轨道不平顺激励下车隧耦合振动进行分析，讨论了流体效应、轨道不平顺、锚索刚度和行驶速度等因素对悬浮隧道动力响应的影响，从中可以得到以下结论：

(1) 悬浮隧道车隧耦合振动同时受到轨道不平顺和流体作用效应的影响。基于数值计算结果，考虑流体作用效应的结构位移有3%左右的增加；而在轨道不平顺激励下，考虑耦合振动的结构位移平均有5%～10%的增加。可见，这种耦合作用效应在振动分析中不应该被忽视。

(2) 悬浮隧道锚索刚度对在轨道不平顺激励用下结构位移响应具有抑制作用。边界和锚索支撑位置附近处，结构振动因边界约束影响受锚索刚度变化影响小；而在其他位置，具有较大锚索刚度的悬浮隧道对轨道不平顺更敏感，局部振动更剧烈。

(3) 车辆行驶速度对悬浮隧道在轨道不平顺激励下车隧耦合振动具有一定的影响。通过比较发现，在高干扰轨道激励下，快速行驶的车辆使耦合系统发生更强烈的振动，故可通过控制车辆行驶轨道的平顺度以降低高速通行要求下产生的车隧耦合振动影响。

文中仅分析了单自由度弹簧质量车在轨道不平顺激励下对于悬浮隧道的车隧耦合振动响应的影响，对于多自由度车辆模型及横向波浪、洋流等共同作用的悬浮隧道动力特性分析有待进一步的研究。