基于激光光斑圆心偏移计算的导轨直线度测量
2019-01-18褚丹丹许新科郭天太
赵 军,褚丹丹,许新科,郭天太,孔 明
(中国计量大学 计量测试工程学院,浙江 杭州 310018)
直线度测量是形状误差测量中非常重要的一项测试内容,同时也是垂直度、同轴度、平面度等误差测量项的基础,对仪器的精度有着直接的影响[1],因此,国内外学者对直线度的测量方法和测试结果做了大量的理论研究和实验论证[2-3].目前为止,测量直线度的方法有很多,根据测量中是否以激光为载体划分,可分为非激光的测量方法和激光类测量方法两大类[4].其中,非激光的测量方法有重力法、水平仪法和测微仪法等,这类测量方法操作简单、成本较低,但其测量结果的精度较低且测量范围有限.相比之下,以激光为载体的直线度测量方法因激光的相干性好、方向性好、抗干扰性强等优点,在实际操作中具有更高的测量精度,因此,更广泛地运用于生产实践中.比较常用的激光类直线度测量方法有激光相位测量法、激光偏振测量法等.激光相位测量法的工作原理是根据干涉光路相位发生的变化,计算被测对象的直线度误差,这种方法能够达到较高的精度,但其测量范围有限;激光偏振测量法的工作原理是通过激光偏振方向的改变来获取被测对象的直线度误差,这种方法不受光斑衍射、窄缝倾斜等影响,但受光学元器件工艺的制约较大[5].
本文通过激光光强测量法,采用激光干涉仪、CCD相机和光学镜组搭建了导轨直线度测量系统,通过图像处理方法获取导轨上每个被测位置采集的光斑圆心坐标,求出每个被测位置的光斑圆心与初始位置光斑圆心的偏移量,利用最小二乘法进行数据处理,最终求得导轨直线度误差.
1 测量系统的介绍
1.1 测量系统的工作原理
从激光干涉仪发射出一束激光,激光束经分光棱镜分光之后,一束光线反射出去;另一束光线根据光路传播原理,到达平面反射镜,并原路返回经分光棱镜被CCD相机接收,获得一初始光斑.当平面反射镜随移动靶标在导轨上移动一段距离之后,形成新的位置的光斑.理论上,将此二光斑拟合在一张图片中时,两个光斑能达到重合,而在实际操作过程中,由于导轨直线度误差的存在,光斑圆心并不完全重合,导轨上有凸起或凹陷,即该位置存在偏折角.
d=D·tanθ.
(1)
其中:θ为测量位置点的偏折角,D为激光的光程,d为两光斑圆心坐标的偏移量.本文着力于根据平面反射镜的移动距离和各测量点测得的光斑圆心与初始位置光斑圆心之间的偏移情况,来求取导轨的直线度误差信息.
由式(2)可求得出两光斑圆心之间的偏移量d:
(2)
式(2)中:(xi,yi)为导轨上任意位置时的光斑圆心坐标;(x0,y0)为初始位置时的光斑圆心坐标.
评定导轨的直线度误差时,在导轨上各测量点测得的光斑圆心是在与初始位置光斑圆心位置所在的中心线lLS平行,且以dmax为半径的圆柱面内[6].其正投影情况如图1.
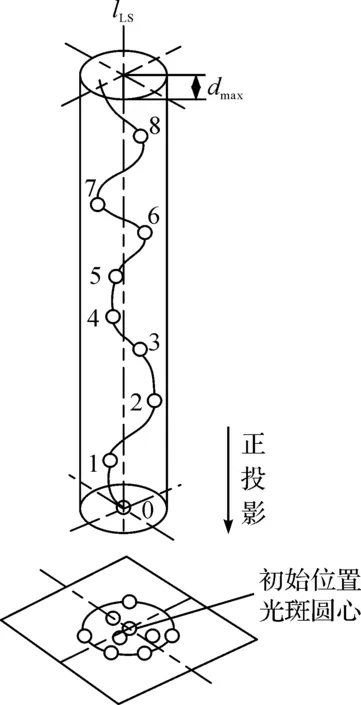
图1 测量点分布图Figure 1 Distribution map of measurement points
1.2 测量系统的组成
测量系统包括机架、激光干涉仪、CCD相机和光学镜组,其架构组成如图2.激光干涉仪和CCD相机固定安装在机架上,在激光干涉仪镜头正前方安装分光棱镜且分光面与水平面成45°,分光棱镜正下方安装CCD相机,确保激光干涉仪发射出的一束激光经过分光棱镜之后一束光线反射出去,另一束光线在经过光路传播回来之后使光斑落在CCD相机的感光面上.平面反射镜固定在导轨的移动靶标上,使光线能沿着平行于导轨的方向传播并反射至CCD相机接收.通过图像处理的方法提取光斑圆心坐标,获得各测量位置光斑圆心和初始位置光斑圆心的相对偏移量;利用最小二乘法求得被测导轨的直线度误差.该测量系统结构简单合理,操作方便,测量精度高,大大提高了检测效率.
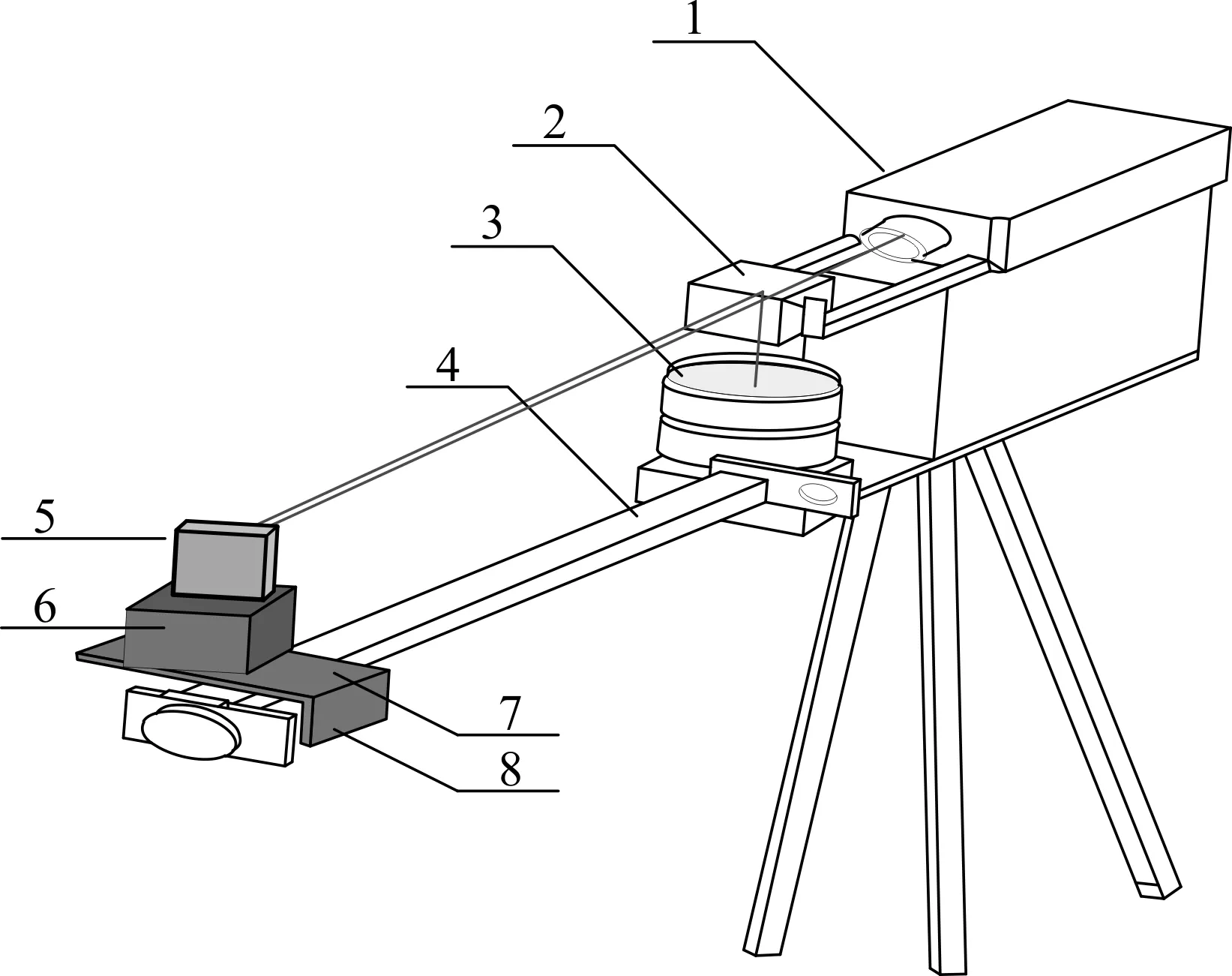
1—激光干涉仪;2—分光棱镜;3—CCD相机;4—被测导轨;5—平面反射镜;6—移动靶标;7—靶标A面;8—靶标B面图2 导轨直线度测量系统Figure 2 Measuring system for straightness of guiderail
2 图像处理及最小二乘法
2.1 光斑的图像处理
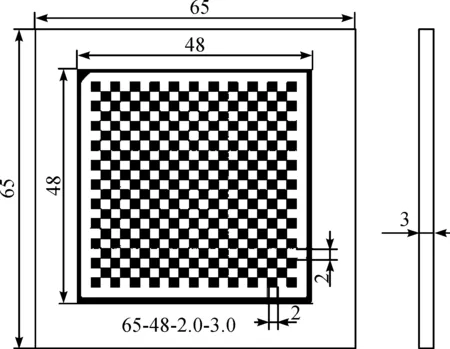
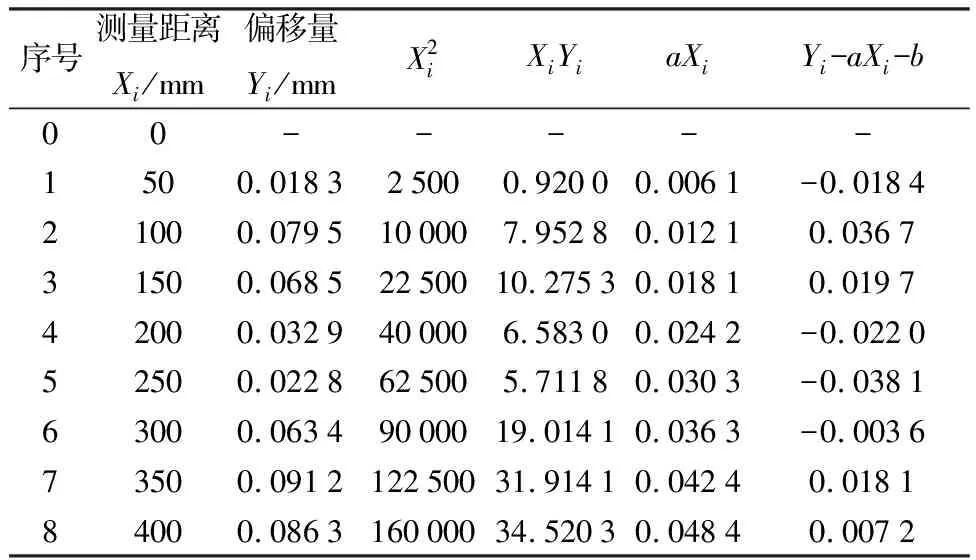
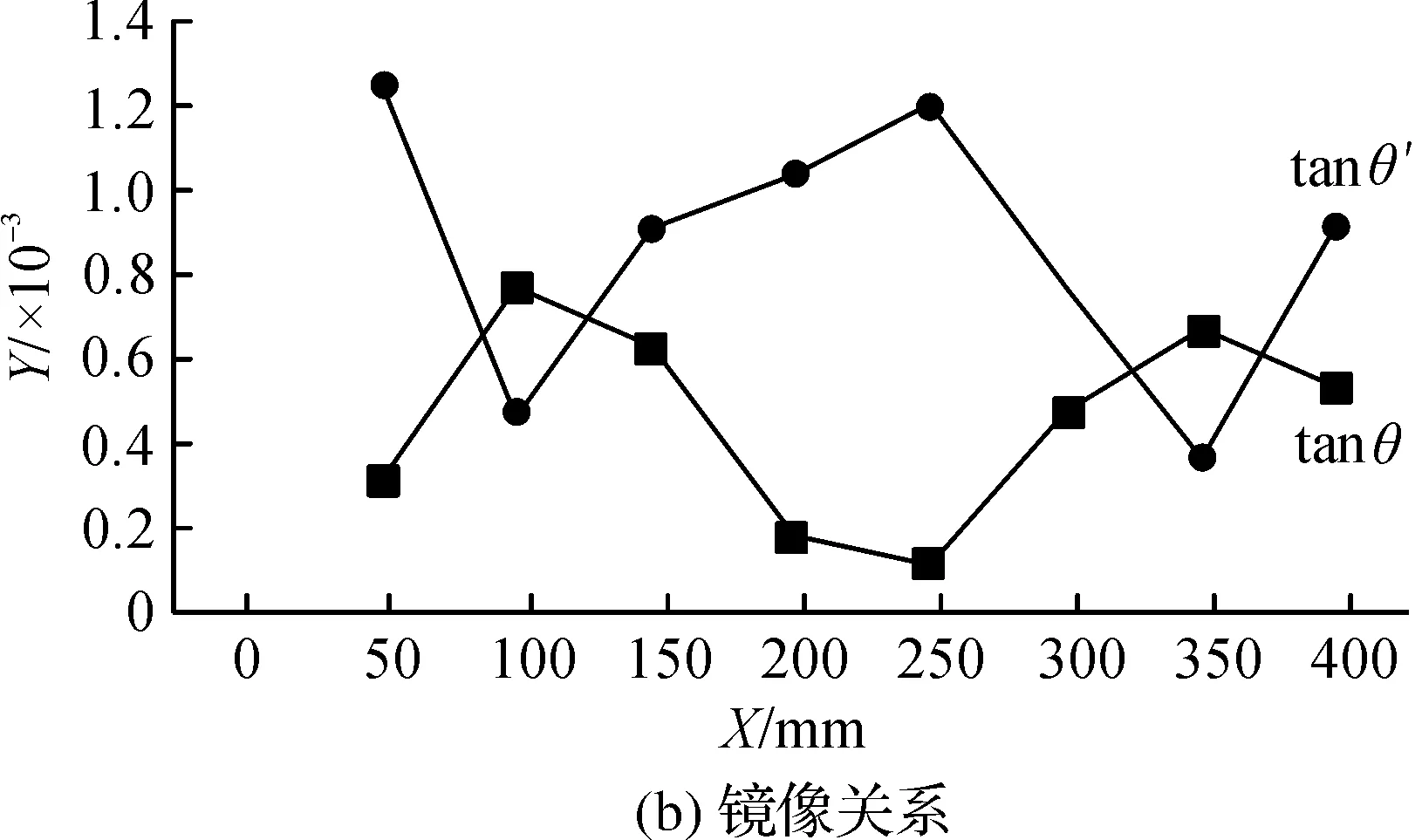
光斑圆心坐标的提取精度直接影响着实验结果的准确性,实验中将采集的图片进行图像预处理之后,利用hough变换进行圆检测[7].传统的边缘检测算子可以分辨被测图像边缘处灰度值较大的位置,但其定位精度只能达到像素级[8],为了提高实验中图像的光斑边缘检测精度,我们采用了三次样条插值法对光斑图像边缘进行插值处理,使光斑边缘达到亚像素级[9],从而提高了后期提取到的圆心坐标值的精确性.
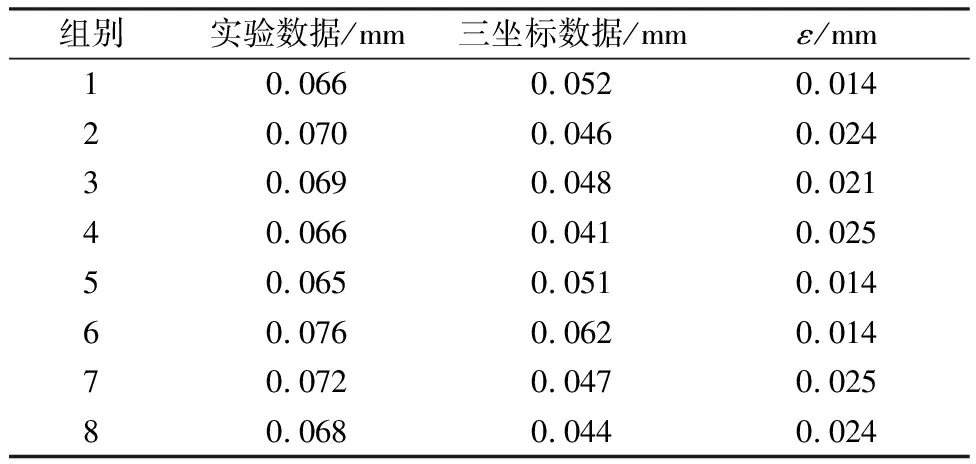
三次样条插值的定义为:若函数S(x)满足:S(x)在每个子区间[xi-1,xi](i=1,2,…n)上是不高于三次的多项式,其中(a=x0 1)S(x),S′(x),S″(x)在[a,b]上连续. 2)满足插值条件S(xi)=f(xi)(i=0,1,…,n),则称S(x)为函数f(x)关于节点x0,x1,…,xn的三次样条插值函数. 在对图像的插值处理中,使用插值函数S(ω),其数学表达式为: (3) 理论上,三次样条插值的最佳插值函数为sinc(ω),而上式中的三次多项式S(ω)正是对函数sinc(ω)的逼近. 取浮点坐标(i+μ,j+v)周围十六个邻点,而我们想要获得的目的像素c的值f(i+μ,j+v)可由如下的插值公式得到 f(i+μ,j+v)=ABC. (4) 其中: A=[S(1+u)S(u)S(1-u)S(2-u)], (5) (6) (7) 对光斑边缘亚像素化的图像进行二值化处理[10],选取最佳阈值对灰度边缘图像进行阈值分割,在选取最佳阈值时,采用的是最大类间方差法,以图像中光斑明亮处和黑色背景的类间方差作为阈值选取的度量准则[11].利用这一准则遍历图像灰度直方图的整个灰度级范围,当阈值在直方图波谷或波谷附近时,图像中光斑明亮处与黑色背景之间的分离特性达到最佳,此时的阈值即为最佳阈值.之后利用hough变换拟合得到圆,在该圆上任取3个点,通过这3个点的坐标确定圆心坐标.图3(a)和3(b)分别为光斑原图和拟合圆之后的图. 图3 光斑原图和拟合圆Figure 3 Original light spot and fitting circle 最小二乘法是一种在多种学科中被广泛应用的数据处理方法,它以最小二乘直线作为评定基准线[12],其中,最小二乘直线即是在残余误差平方和最小的条件下求得的一条直线[13]. 基于Matlab软件进行图像处理后得到的数据是像素单位,实验采用黑白棋盘格标定法对CCD相机进行了标定. 标定的目的是获得图像中每个像素对应的实际尺寸,用到的标定板中每一方格为2 mm×2 mm,图4为标定板的尺寸图.令CCD分别在距离标定板30 cm、40 cm、50 cm位置获取棋盘格图片,计算得到这些位置时图像中每个像素的大小对应的实际尺寸大小分别为0.003 418 mm、0.004 407 mm和0.005 399 mm.根据线性关系拟合得到直线y=0.000 099 05x+0.000 446 5,其中,x是距离,单位cm;y是实际尺寸,单位mm.实验测量时,CCD相机与导轨上最近的测试点距离为79 cm,最远点距离为119 cm,由拟合直线可分别获得各个测量位置光斑圆心坐标的物理坐标. 图4 棋盘格标定板尺寸Figure 4 Checkerboard calibration board size 根据各测得点的坐标,用最小二乘法计算直线度误差[12],设最小二乘方程为y=ax+b,参考式(8)、(9): (8) (9) 得a=0.000 121 0;b=0.030 7,则最小二乘直线方程为 y=0.000 121 0x+0.030 7. 将最小二乘计算法以列表的形式进行,其中,正数最大值与负数最小值绝对值之和即为所求直线度误差,fLS=|0.036 7|+|-0.038 1|≈0.075 mm,见表1第7列数据. 表1 最小二乘法计算直线度误差Table 1 Calculation of straightness error by least square method 实验平台中,被测导轨长为60 cm,故实验操作时,在导轨上每隔5 cm获取一张实验光斑图片,一组实验共获取9张图,在第一个测量位置获取的光斑图像作为参考点,称为初始光斑图片,靶标等距离移动到位置1,2,3…i(i=8)获取的图片即为各测量点光斑图片.将CCD采集的图片通过Matlab进行图像处理,分别求得各光斑圆心坐标. 光斑圆心坐标给出的信息是导轨的空间直线度情况,根据各测量点光斑与初始光斑圆心坐标的偏移量,可以分离出被测导轨分别在X-Y平面和X-Z平面的单维直线度误差.在实验操作中,使用三坐标测量机对导轨的直线度进行了同步测量. 获取导轨在X-Y平面的单维直线度误差,当装有平面反射镜的移动靶标每次停顿在导轨上的一个测量位置时,通过CCD获取对应光斑图片,同时用三坐标测量机按靶标移动方向在靶标A面采点(锁定三坐标测量机X轴方向).通过式(10)可求得 (10) 其中,θ′为三坐标测量机在对应测量位置测得的偏折角,Δh为两个相邻测量点之间的Z坐标之差,L为两点之间的Y坐标之差.将tanθ′与光斑圆心坐标偏移量中分离出来的单轴直线度信息对比,能够找出两者之间的对应关系. 同理,在靶标B面按其移动方向采两个点(锁定三坐标测量机Z轴方向),数据处理后,可求得导轨在X-Z平面的单维直线度误差. 表2 X-Y平面实验数据采集Table 2 Experimental data collection of X-Y plane 由拟合曲线可知,在X-Y平面,实验方法计算得的tanθ与三坐标测量机数据求得的tanθ′曲线趋势一致,如图5(a).同理可得,在X-Z平面可知tanθ与tanθ′曲线成镜像关系,如图5(b). 图5 实验数据与三坐标测量机数据对比Figure 5 Comparison between experimental data and tri-coordinate measuring machine data 由实验结果可知,本光学测试系统能够测试导轨的空间直线度误差,并且将光斑圆心坐标中的Y坐标偏移量提取出来能够单独求得X-Y、X-Z平面的直线度误差.数据处理结果与三坐标测量机测得的情况一致. 利用最小二乘法求导轨在X-Y面的单轴直线度误差,计算结果如表3,其中误差ε=实验数据-三坐标数据. 表3 实验数据与三坐标测量数据对比表Table 3 Comparison table of experimental data and tri-coordinate measuring data 由表3可知,实验测得的误差数据均比三坐标测量机的数据大.理论上,测量系统中分光棱镜的分光面与CCD相机相面之间的夹角为45°,但实际搭建系统时存在一定的偏转,且分光棱镜与CCD相机之间的距离越大,夹角偏转量对实验结果的影响就越大.实验中通过电机控制靶标移动,电机的分辨率大于激光干涉仪的分辨率,不能给出测试点更高精度的定位,此外,实验操作中被测导轨上靶标移动时的振动以及提取光斑圆心坐标的精确度也对测量结果有一定影响.将多组数据进行分析比较,实验中所用的三坐标测量机精度在10 μm,根据ε可知,本实验测量系统的测量精度在40 μm左右. 提出了一种基于多数据融合的测量方法,实现了导轨的单维和空间直线度误差测量[14],将实验数据与三坐标测量机测得的数据进行了对比,实验结果证明,本测试方法分离出的单维直线度误差趋势与三坐标测量机测得的数据拟合得到的导轨直线度误差趋势有很好的对应关系.通过最小二乘法可得到导轨的空间直线度误差,实验表明,本测试系统具有运行稳定、精度高等优点,相比较三坐标测量机具有成本低、灵活性强、测量范围广等优点.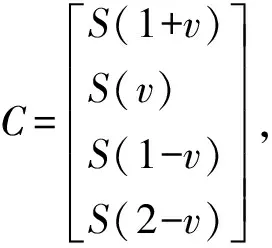
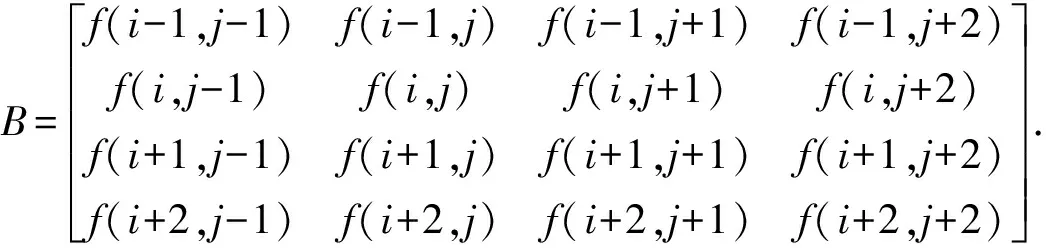

2.2 最小二乘法
3 实验数据采集及处理
3.1 实验数据的采集
3.2 实验结果及分析


4 结语
