提升认识 独立思考

张弟红

【摘 要】 《一元二次方程》是人教版七年级上册的内容，本章节的知识点是学生初中数学生涯的重要节点，学习一元二次方程为今后的学习打下基础，帮助学生建构模型思想，为学习深层的方程式和函数添砖加瓦。

【关键词】？初中数学；一元二次方程；独立思考

一元二次方程作为初中数学教学的初始知识，在初中数学中占据重要地位，一元二次方程作为后续的二次函数、二次曲线、不等式、指数和对数方程等众多数学知识学习的前提条件，会直接影响后续知识点的数学学习效果。一元二次方式不只是单单传授一种方程的概念，更主要的是传授一种独立思考能力和数学思维能力，建立正确的一元二次方程对实际问题进行解答。

一、攻克教学难点

一元二次方程是只含有一个未知数，未知数的最高次数是2，等号两边都是整式的方程。因此在教学活动中，一元二次方程的教学难点在于数量关系分解和方程解题思路，攻克教学难点的内容如下：

首先是数量关系分解，学生要了解一元二次方程的知识点和概念，根据一元二次方程的内容进行概括和归纳，一元二次方程学习要先从一元一次方程开始，回顾并巩固方程式的有关知识点，充分预习相关知识点，对一元二次方程中的数量关系有清晰直观的了解，学生可以在阅读中思考一元二次方程的问题，根据题目的意思列出相应的方程，从而了解到方程形成的概念，让方程从书本上进入思维里，学生会独立思考解题思路和解题范围，通过经验的积累可以提高学生的独立思考能力。此阶段可以提出相关的基础知识点考查题目，例如，下列方程中是关于x的一元二次方程的是（ ）

其次是方程解题思路，一元二次方程的应用形式多样，包括周长问题、面积问题、利润问题等，比如周长问题就要先明晰知识点与题目的联系，根据题目要求建立一元二次方程，找到题目之间的内在联系，让学生通过对问题分析感受到方程在现实世界中的运用，找出其中的等量关系列出方程。通过长期锻炼，让学生形成一元二次方程解题思路模式，逐渐培养思维能力和逻辑能力。比如面积问题：如图，在宽20米，长32米的矩形耕地上修筑同样宽的三条路（两条纵向，一条横向，并且横纵线相互垂直），通过三条路把这块耕地分成大小相等的六块田，要使每块田的面积为570平方米，道路宽度应为多少？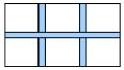

分析题目可知，可以先设未知数，设道路宽度为x米，从题目概念可知20×32-20x×2-32x+2x2=570，设立方程步骤可以训练学生的解题思路，总结思维模式。

二、教学内容解析

结合教学内容、学生学习情况开展教学内容解析，制定相关教学方案，教学内容要从认知基础和巩固基础出发，利用学生在小学时期积累的简易方程知识为切入点，让学生对数学知识表层浅意的理解变得深入，知识体系规范性、严谨性，从简单的计算思维进化为代数思维，要结合学生的心理特点，从学生的学习兴趣点出发，以生动活泼的课堂教学氛围引导学生投入学习，通过创设问题情景，以问题去引导学生思考，再通过教师讲授，结合学生回答情况进行相关知识点教学。可以设置两个相关联的题目，通过不同的解题角度进行思考交流，再比较两种解题步骤有何差异和共通之处，引出本节课所讲的重点。

比如：（1）某钢铁厂去年一月份某种钢的产量为5000吨，三月份上升到7200吨，这两个月平均每月增长的百分率是多少？（2）某产品原来每件600元，由于连续两次降价，现价为384元，如果两个降价的百分数相同，求每次降价百分之几？

这两道题都考查的是有关增长率的平均變化率问题，要让学生辨析清楚“增长”“下降”的方程，设置两个未知数，向学生说明相关区别。题（1）需设平均每月的增长率为x，设某产量是a，则增长一次后的产值为a（1+x），增长两次后的产值为a（1+x）2，……增长n次后的产值为S=a（1+x）n，带入题目可列方程为5000（1+x）2=7200。题（2）需设每次降价为x，则产值a经过两次下降到b，可列式为a（1-x）2= b，根据题意可得方程为600（1-x）2=384。从一个知识点的两个不同方向出题，利用有共同解题思路的方程式让学生对算数方程解法进行相关归纳，总结规律。

三、思维模式建构

通过数学相关知识练习“建立数学模型”，提高学生对题目内容的抽象概括能力，用多种不同形式的题目丰富学生思考、讨论的方向，克服小学单一算数思维教学方式所形成的固定思维，引导学生形成建模思维，归纳相关一元二次方程的概念，通过不同形式的题目，用对比的方式让同学们对一元二次方程概念的认识加深，增强学生对题目的理解能力。

学生在一元二次方程的学习过程当中，通过建立数学思维模型解答题目，拓展相关知识概念，将方程模型思想运用到数学思维解答过程当中，提高了应用意识，对一元二次方程的含义有深刻理解，在后续学习知识的过程当中，体会到运用方程思维模式去解决实际问题的有效性，在简单的背景问题分析过程当中分析已知数和未知数之间的数量关系，提升对一元二次方程的认识，独立思考总结相关数学知识点，提升学生数学思维模式建构。

【参考文献】

[1]张永华.例谈培养初中数学思维能力的教学策略——以九年级《一元二次方程》单元教学为例[J].福建中学数学，2017（12）.

[2]姚丽宁，蔡建锋.《一元二次方程应用复习》教学设计与点评[J].中学数学教学，2010（2）：6-9.