弘扬数学文化 提升试题内涵
——以近两年浙江省数学中考试题为例
2019-01-16
●
(浙江师范大学教师教育学院,浙江 金华 321004)
1 问题的提出
我国在新课程改革中十分重视数学文化的教育价值,提升国民的数学素养必须厘清数学文化的本质,把数学文化理念贯穿到基础教育的整个过程中.《义务教育数学课程标准(2011版)》中指出:“数学是人类文化的重要组成部分,数学素养是现代社会每一个公民应该具备的基本素养.……数学教育……更要发挥数学在培养人的理性思维和创新能力方面不可替代的作用.”[1]可见,数学不仅是一项帮助我们解决现实问题、提升物质生活水平的技能,还是一种文化影响着我们的思维.近几年,全国各省市的数学高考命题积极融入数学文化因素,设计了很多具有深厚文化底蕴、趣味盎然的优秀题目[2-3].这种命题风格在一定程度上影响着数学中考的命题取向.本文通过对浙江省近两年中考数学试卷中涉及数学文化背景的试题进行分析,希冀能对中考试题的设计提供一些建议.
2 数学文化背景试题的内涵与意义
数学文化,简单说,是指数学的思想、精神、方法、观点以及它们的形成和发展;广泛些说,除了上述内涵以外,还包含数学家、数学史、数学美、数学教育、数学发展中的人文成分、数学与社会的联系、数学与各种文化的关系等等[4].而数学文化背景试题是指数学试题的考查方式将结合数学文化的因素加以呈现.数学试题设计融入数学文化背景,具有如下几个意义:
1)促使试题设计更加灵活多样.
数学文化背景试题的创设为试题命制者提供了更加开阔的命题视野,使得他们命题时不再局限于单一的数理方向,在命题时可以选取更加丰富的材料.比如在命制“勾股定理”这个知识点的试题时,试题命制者就可以结合《几何原本》中欧几里德的证明方法及相关背景进行命题,而不是简单的勾股定理的公式运算和简单应用.
2)提升学生的数学文化素养.
数学文化对于人的发展具有十分重要的作用.而数学试卷中设计数学文化背景试题可以使学生在润物细无声中感受数学的美,从中看到人类为追求真理而奋斗不息的历史画卷,从而被那种为追求真理而矢志不渝的求知精神所震撼,学生也在这种试题中感受了良好的人格品质——追求真理.也许,这就是数学文化背景试题的设计初衷.
3)体现数学试卷的文化内涵.
数学试卷不仅是学生数学学习成效的测验工具,也凸显着深厚的文化内涵.一份设计优秀的数学试卷不仅考查学生对数学知识的掌握程度,而且也承担着学生文化素养培养的使命.例如数学试题中穿插着一些数学家的事迹,就会启发学生考试结束后去查阅相关资料,追寻数学家的成长足迹,使得学生了解数学家漫漫求索的艰辛历程,其坚韧的品格定会激励着学生进一步探索知识.由此,数学试卷不仅仅是一个测验工具,而且还散发着人文关怀,以其深厚的文化内涵教育学生“成人”.
3 中考数学试题中的数学文化
本文以2017和2018年20套浙江省各地数学中考试卷为例进行分析.正如前文所述,数学文化的融入使得试题设计更加灵活多样,使得数学试卷更具阅读的美感,提升了数学试卷的文化内涵.
3.1 突出数学与自然科学的联系
数学是自然科学的基础.在现代自然科学的发展中,数学起到了决定性的作用,是我们打开自然界秘密花园大门的一把金钥匙.在数学试卷中设计一些与自然科学相关的试题有利于加强学生对于数学作用的理解,提升学生学习数学的兴趣.
例1太阳与地球的平均距离大约是150 000 000 km.数据150 000 000用科学计数法表示为
( )
A.1.5×108B.1.5×109
C.0.15×109D.1.5×107
(2017年浙江省杭州市数学中考试题第2题)
例22018年5月25日,中国探月工程的“鹊桥号”中继星成功运行于地月拉格朗日L2点,它距离地球约1 500 000 km.数1 500 000用科学计数法表示为
( )
A.15×106B.1.5×106
C.0.15×107D.1.5×105
(2018年浙江省嘉兴、舟山市数学中考试题第2题)
这两题考查的是科学计数法的掌握程度.科学计数法在科学研究中被广泛使用,为人们表达一些冗长的数据提供了方便,节省了时间,这也体现了数学的简洁美.这两道试题的设计结合了自然科学的材料,学生在阅读题干时也能了解一些自然科学与数学的紧密联系,也使得学生体会到了科学计数法的重要作用.
3.2 融入数学史
恢弘雄伟的数学大厦吸引着无数慕名而来的求知者,深深地吸引着广大数学爱好者.数学试题中积极融入古圣先贤的数学成就,使学生在做题的同时感受人类数学发展史中“慎思、笃行、求精”的精神,了解我国辉煌璀璨的数学历史成就.

图1
例3我国三国时期数学家赵爽为了证明勾股定理,创制了一幅“弦图”,后人称其为“赵爽弦图”.在图1中,若正方形ABCD的边长为14,正方形IJKL的边长为2,且IJ∥AB,则正方形EFGH的边长为______.
(2017年浙江省丽水市数学中考试题第15题)

图2
公元三世纪,三国时代的赵爽对《周髀算经》中的勾股定理作出了详细注释,记录于《九章算术》中“勾股各自乘,并而开方除之,即弦”,赵爽创制了一幅“勾股圆方图”,用数形结合得到方法,给出了勾股定理的详细证明.2004年第四届国际数学家大会(ICM)的会徽即为“赵爽弦图”,这也足以说明国际上对于我国古代数学成就的肯定.本题的设计不仅让学生了解了赵爽的数学成就,领略了我国古代人民卓越的数学贡献,而且考查了学生对于“勾股定理”的掌握情况.
例4七巧板是我国祖先的一项卓越创造.下面4幅图有3幅图是小明用如图2所示的七巧板拼成的,不是小明拼成的那幅图是
( )

A. B.

C. D.
(2017年浙江省湖州市数学中考试题第9题)
七巧板是我国古代发明的一种儿童益智类玩具.因其利用7块基本图形可以组合成丰富多样的图案,可以极大地锻炼儿童的智力,因此也叫“东方魔板”.本题以七巧板为设计材料,主要考查学生的基本几何知识,这里面涉及到几何图形的变换组合、特殊几何图形的边角关系以及学生的观察与想象能力.例4将中国古代贤达的数学智慧和数学知识进行了完美的结合,它不仅考查了学生的数学知识,发展了学生的思维,而且还提升了数学试题的内涵.数学不再是单调的数理推演,它还能充满童趣地进行人文素养的熏陶.
3.3 突出数学与生活的联系
21世纪是信息化的时代,也可以说是数字化的时代.在这个信息如狂风暴雨般向我们迎面扑来的数字化时代,如何保持自己的理智,如何跨越“数字化的陷阱”,如何利用信息更高效、快捷地达成目的,这就需要我们善于在生活中运用数学知识和思维去甄别虚假信息,从而过上理智、高效的生活.而呈现生活化的试题,有利于学生养成数学的理性思维方式,有助于学生运用数学知识、方法与技能去解决实际中的问题.
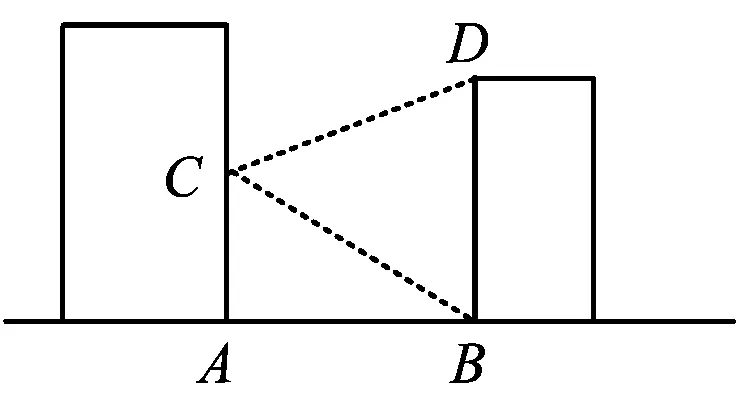
图3
例5如图3,学校的实验楼对面是一幢教学楼,小敏在实验楼的窗口C测得教学楼顶部D的仰角为18°,教学楼底部B的俯角为20°,量得实验楼与教学楼之间的距离AB=30 m.
1)求∠BCD的度数;
2)求教学楼的高BD.
(结果精确到0.1 m,参考数据:tan 20°≈0.36,tan 18°≈0.32.)
(2017年浙江省绍兴、义乌市数学中考试题第20题)
我国基础教育的训练方式存在着一些问题,传统的训练方式导致习题与生活现象脱节,因此可以从学生的生活中提炼试题来解决一些问题.而例5很好地向我们呈现了试题命制的“生活化”取向,它从学生的日常生活环境(学校建筑)中选取命题材料,这不仅给学生一种亲切感,而且启发学生关注生活,“世事洞明皆学问”,一定要善于观察生活世界.
4 思考与建议
可以说,数学试题融入数学文化为试题命制者提供了更加开阔的命题视野,锻炼了学生的数学阅读和理解能力,提升了学生的数学文化修养.
2017年浙江省数学中考命题专家们进行了积极探索,大胆地进行实践创新.该中考试卷不仅考查学生的数学知识能力,还非常注重数学试题与数学文化的融合,注重提升学生的文化素养,为中考试题的命制提供新的范式,体现了浙江省义务教育改革“立德树人”的指导精神.随着浙江省义务教育课程改革的深化推进,数学文化也在积极地走进教材、走进课堂,但“如何进行数学文化教育,如何让学生体会数学文化的丰富内涵”还是一个亟待研究的课题.数学试卷中积极地融入数学文化是数学文化教育的一个重要手段,但这还需要创新命题的方式,以更加多样的形式让数学试题与数学文化融合.浙江省数学中考试题中的数学文化体现形式过于单一,主要是以一些选择题和填空题为主,这很难弘扬数学文化的魅力,因此数学文化与数学试题的融合还要进行创造性的研究.
数学思想方法在人类文化的画卷中留下了浓墨重彩的一笔.数学是人类科学的皇冠,那么数学思想方法则是人类仰望星空时的启明星,照亮前进的道路,它以其精确、严谨的思想方法为人类每一次在迷茫中的探索提供了起航的坐标.而试卷中设计一些与经典数学思想方法相关的试题则有利于学生对数学思想方法的迁移运用.
例6阅读材料,大数学家高斯在上学读书时曾经研究过这样一个问题:
1+2+3+……+100=?
经过研究,这个问题的一般性结论是
其中n是正整数.现在我们来研究一个类似的问题:
1×2+2×3+……+n(n+1)=?
观察下面3个特殊的等式:
将这3个等式的两边相加,可以得到
阅读这段材料,请你思考后回答:
1) 1×2+2×3+…+100×101=______;
2) 1×2+2×3+…+n(n+1)=______;
3) 1×2×3+2×3×4+…+n(n+1)(n+2)=______.
(只需写出结果,不必写中间的过程.)
(2005年四川省内江市数学中考加试卷第6题)
数学教学首先是一门语言的教学,例6首先是让学生阅读材料,锻炼了学生的数学阅读理解能力.学生通过这则材料的阅读了解到高斯的数学事迹,启发学生要善于思考.通过阅读材料,启发学生运用类比思维进行归纳总结,从而解答题目.例6也生动地展现了类比归纳的数学思想精髓,且题目设计为3个小问题层层递进,启发学生思考问题要循序渐进,遵循一定的逻辑序列.
