关注基本模型 形成解题程序 提升核心素养——对一道中考题及其变式的解法探究

●

(坪地中学,广东 深圳 518116)

在初三中考数学备考过程中，教师应引导学生通过对基本模型的探究，透析数学问题的本质，使学生完善自身的数学认知体系，形成解决某类问题的思路、步骤，即问题解决程序，提升数学思维的灵活性和深刻性，发展数学核心素养.本文以一线三等角模型及其变式为载体，研究一道以此基本模型为背景的中考题.

1 “一线三等角”基本模型及其变式

如图1，点B,C,D在同一直线上，且∠B=∠ACE=∠D,我们称这一基本模型为“一线三等角”模型.易知△ABC∽△CDE，如果添加条件AC=CE，那么△ABC≌△CDE.当∠B=∠ACE=∠D=90°时，如图2所示，我们也称该模型为三垂直模型.

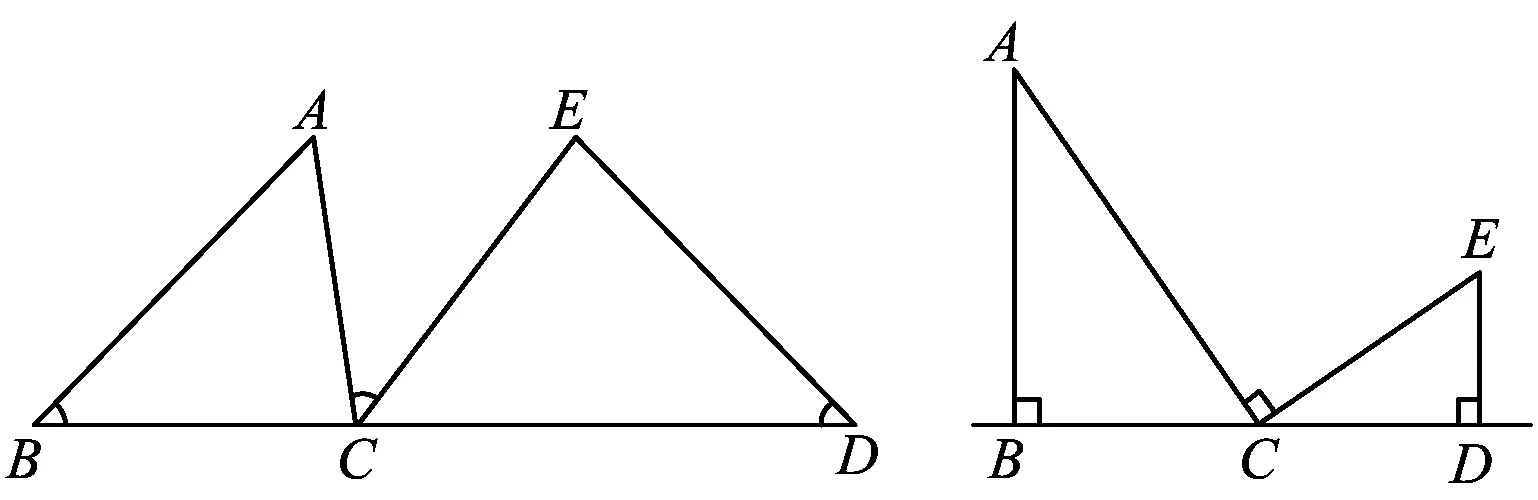
图1 图2

如果在平面中存在点F,使得点A,C,E,F共圆，那么“一线三等角”模型有如下变式.

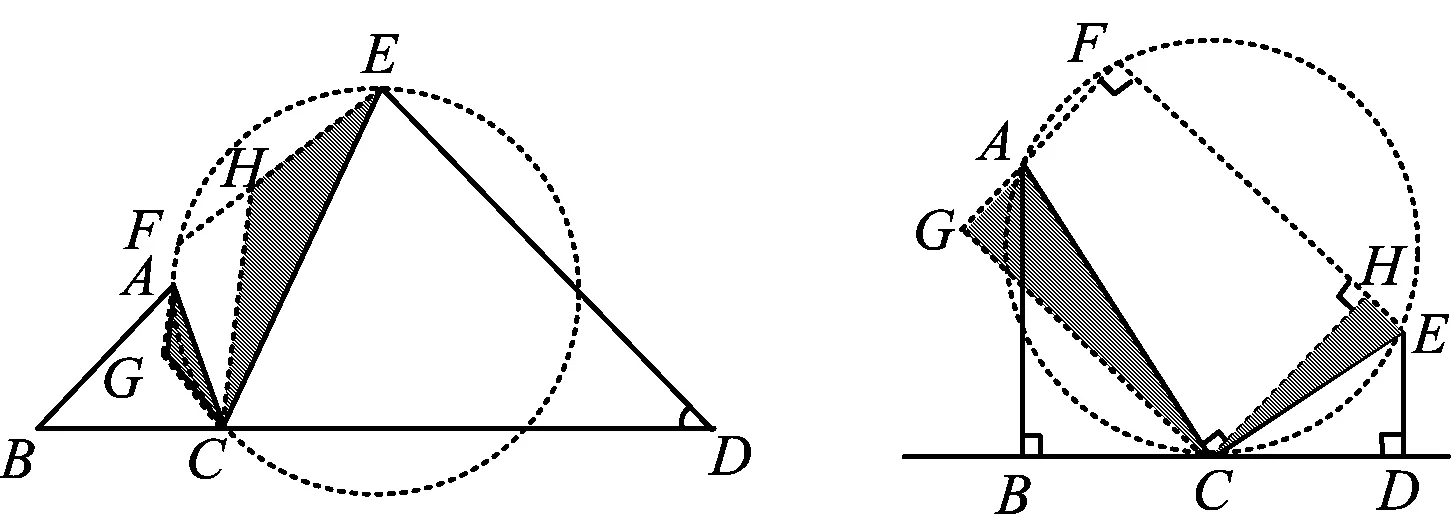
图3 图4

如图3，过点C作CH∥FA交EF于点H,在射线FA上找一点G，使得∠GCH=∠ACE，易知此时△AGC∽△EHC.与图2对应的情况如图4所示.

该模型及其变式在近年来各省市的数学中考试卷中经常出现，部分题目难度较大.深刻了解该模型的特点，可以帮助学生看透数学问题的本质，进而轻松解决问题.

2 试题呈现

图5

例1如图5，在四边形ABCD中，AB=AD，∠BAD=∠BCD=90°，联结AC.若AC=6，则四边形ABCD的面积为______.

(2017年陕西省数学中考试题第14题)

本题是一道中档难度填空题，具有一定的难度，思维含量高.该题以直角三角形为背景，综合考查了圆的内接四边形的性质以及构造全等三角形和特殊四边形解决问题的能力，综合性较强.

3 解法探究

根据题意，考虑到△ABD和△BCD是直角三角形，由垂直可构造特殊四边形，从不同角度分析可以探索出多种解题思路.现举例如下:

思路1原图形对角线AC已将四边形ABCD切分为△ADC和△ABC,故求出△ADC和△ABC的面积之和即可.过点B作BF⊥AC于点F,过点D作DE⊥AC于点E，联结BD,如图6所示.由于△ABD是等腰直角三角形，易证△ABF≌△DAE,因此BF=AE.注意到∠BAD+∠BCD=180°，故点A,B,D,C共圆.此时，∠BCA=∠BDA=45°，即△BCF是等腰直角三角形，故BF=FC.因此，

S四边形ABCD=S△ABC+S△ACD=

评注在思路1的解决方案中我们发现：点A,B,D,C共圆，注意到∠BCA=∠BDA=45°，故∠ACD=45°，可以考虑以AC为对角线构造等腰直角三角形，进而解决问题.

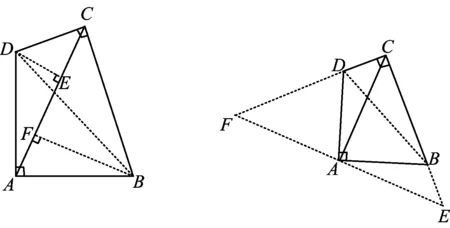
图6 图7

思路2过点A作直线EA⊥AC,交CB的延长线于点E,交CD的延长线与点F,如图7所示.联结BD,由于△ABD是等腰直角三角形，易证△ADF≌△ABC.此时求四边形ABCD的面积转化为求等腰Rt△CAF的面积.易求得△CAF的面积为18.

评注注意题目给出的问题特征，可构造三垂直模型或其变式(图2和图4)，搭建问题线索，形成解决程序.

思路3过点A作AF⊥BC于点F,作AE⊥CD于点E，如图8所示.由于AB=AD，易证△EDA≌△FBA,且四边形ECFA是正方形.此时求四边形ABCD的面积转化为求正方形ECFA的面积.由对角线AC=6，易求得正方形ECFA的面积为18.

图8 图9

思路4过点C作CE⊥AB于点E，作CF⊥AD的延长线于点F，如图9所示.易证△CBE∽△CDF,且四边形ECFA是矩形.设AB=AD=m,∠CAE=α,则

CF=AE=6cosα，CE=6sinα,

从而

BE=m-6cosα，FD=6sinα-m.

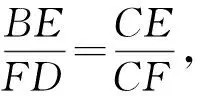
故S四边形ABDC=S梯形AFCB-S△CFD=

图10

思路5过点C点作EF⊥AC，交AD的延长线于点E,交AB的延长线于点F,过点D作DG⊥EF于点G,过点B作BH⊥EF于点H，如图10所示.

设AB=AD=m,∠CAF=α,从而

于是

同理可得

BH=6-mcosα.

由△ADC∽△FBC,易得

故S四边形ABCD=S△AEF-S△CED-S△BFC=

说明本题有两个核心的问题表征：1)四边形中点A，B，C，D共圆；2)△ABD和△BCD是直角三角形.虽然以上5种思路都是通过割补法来求四边形ABCD的面积，但思路1和思路2解法简洁，在运用转化方法的过程中，需深度挖掘和利用四点共圆这个隐性条件；思路3利用三垂直模型进行切入剖析，构造全等三角形，解决方法简洁漂亮，抓住了问题的关键；思路4和思路5虽也从三垂直模型角度出发，通过构造相似三角形进而解决问题，但由于Rt△BCD的边长关系无法确定，因此处理起来相对繁琐；思路4和思路5通过引入变量，最终化简消元，体现了数形结合的数学思想，能更清晰地感悟到变中不变的规律.

教师可引导学生通过对不同解法的探究和感悟，利用图形特征，搭建问题线索，初步形成本题的解题程序的为：直角三角形—三垂直模型—构造相似三角形.若问题中存在等腰直角三角形，则应优先通过其构造三垂直模型找全等三角形，将其作为解决问题的切入点.

实际上，若给定Rt△ABD的边长关系和边AC的长度，则例1也可以拓展得到结论：

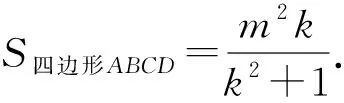
图11 图12

分析过点A作AE⊥BC于点E，作AF⊥CD于点F，如图12所示.易证四边形EAFC是矩形，此时△EBA∽△FDA，从而

假设AF=n(其中n>0)，则

AE=kn.

依题意可得AF2+AE2=AF2+FC2=AC2，

即

k2n2+n2=m2，

于是

故

4 变式推广

变式1如图13，在四边形ABCD中，AB=AD，∠BAD=120°，∠BCD=60°，联结AC.若AC=6，则四边形ABCD的面积为______.

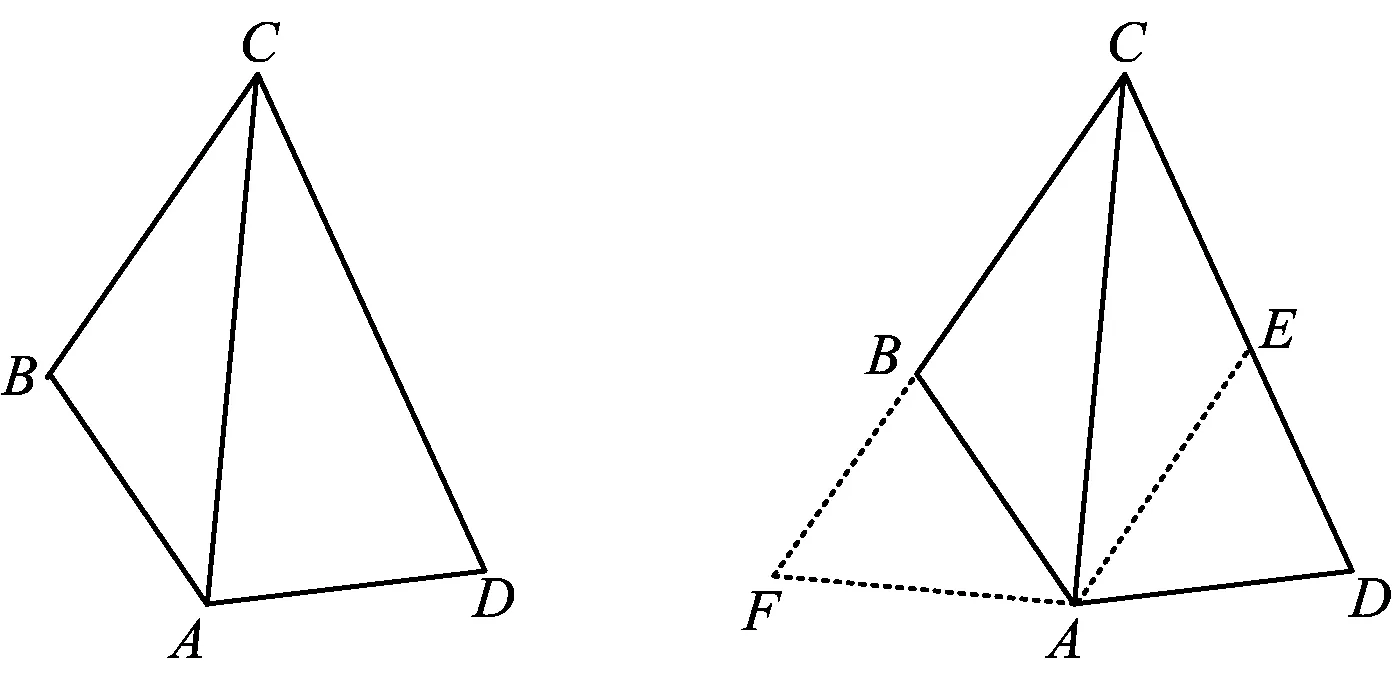
图13 图14

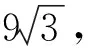
CN=4x，DN=4y,

从而

AN=CN-AC=4x-6，

AM=CM+AC=3y+6.

由BM=AN,AM=DN,易求得x=6,y=6.此时

S四边形ACBD=S梯形MBDN-S△MBC-S△AND=504.

说明变式1改变原题中直角三角形背景，将原来三垂直模型进一步拓展到更一般的一线三等角的情况.学生刚形成的处理程序将在变式1的解决中得到进一步提升，并利用其解决问题.变式2将原题目中△BCD沿着BD翻折，使得点C和点A在线段BD的同侧，此时为了求四边形ACBD的面积，需给出△BCD的边角关系.变式2的解决依旧需从三垂直模型角度切入去解决问题，需要两对相似三角形，难度较原题有所提高.当然，变式2也有类似于结论1的推广，留给读者思考.

5 总结感悟

在初三数学中考专题复习的教学中，解题教学是主旋律.但教师很容易陷入“以题论题”的教学误区中，仅仅停留在把题目的答案求解出来，从而课堂变得枯燥无味，缺乏新知生成，学生思维能力的灵活性和深刻性很难得以进一步的提升.通过该中考题解法和变式的探究，笔者对“如何在几何教学中发展学生的数学核心素养”有了进一步的思考.

首先，关注基本模型，聚焦问题表征.初中几何教学中，教师可设计“折一折、摆一摆、拼一拼、量一量、画一画、剪一剪”等具体直观的活动方式[1]，帮助学生更好地探索解决问题的思路，猜想结果，发展学生的直观想象素养.教师在此过程中引导学生思考解决思路的异同，通过类比归纳，寻找几何图形中存在的基本模型，搭建问题线索，立足从问题表征的角度去比较问题解决思路的异同，形成初步解题程序.

其次，抓住通解通法，形成解题程序.通解通法是解决某类问题最合理的想法、最基本的思路、最普遍的操作程序[2].通过一题多解、多题归一，让学生掌握处理一个基本模型的方法，理解方法背后所隐含的数学思想，知道如何应用到其他情境中去，发展学生的数学建模素养和逻辑推理素养.变式训练变化的是题目，不变的是通法通解，通过对问题变式的探究和原问题的推广，帮助学生掌握一类数学问题的通解通法，进而形成解题模块.

总之，一线教师要有基本的钻研精神，遇到问题不能浅尝辄止，应考虑有无其他解法，解法是否具有一般性，通过一个问题彻底理解一类问题.只有教师抓住知识的本质，创设合理情境，启发学生思考，才能让学生在掌握所学知识和技能的同时，感悟知识本质，积累数学基本活动经验，形成和发展核心素养.