一种双向多跳中继选择算法与信息交互模型
2019-01-16王文敬李展州欧阳汉杰
王文敬,李展州,欧阳汉杰
(中国民用航空飞行学院 航空工程学院,四川 广汉 618307)
0 引言
为了扩大信号的覆盖面,中继通信[1-2]已成为无线通信的一项重要技术。在协同通信中,通常一个网络包含多个中继辅助通信双方进行多跳信息传输,此时的一个关键问题是如何从大规模的中继网络中选择出每一跳的最佳中继[3-4]。
在多跳中继选择中,文献[5]提出了一种在线性多跳网络中,基于解码转发(Decode Forward,DF)协议的多跳中继路径选择方案,为了减小端到端的中断概率,对中继展开了穷尽式搜索,然而它没有考虑通用的中继网络。文献[6]提出了DF协议与网络编码相结合的多条传输模式,并推导了其误符号率在瑞利信道下的闭式。文献[7]基于DF协议,利用瑞利信道模型,研究了一种基于多跳中继最优路径选择的最大-最小中继选择准则,给出了最大-最小指数随机变量的累积分布函数和概率密度函数。文献[8]基于低信噪比的瑞利信道传输中信号丢失的问题,在两跳和三跳传输模式下,通过设置周期阈值,基于信道平均衰落周期提出了一种中继选择策略,并推导了平均衰落周期的闭式。文献[9]同样以减小端到端中断概率为目的,提出了多跳中继网络的最优路径选择策略,同样通过对最优路径的穷尽式搜索,最大化端到端的信噪比,但是其实施要求的计算复杂度非常高,且对内存的需求量特别大,所以对于跳数较多的大规模的网络来说不具有可行性。
为了克服上述缺陷,文献[10]引入维特比译码技术,提出了一种单向传输下的多跳中继选择算法。本文在此基础上,进一步研究了双向传输下的多跳中继选择算法,在高信噪比时,一条多跳路径的等效信噪比的倒数由此路径上瞬时信噪比的倒数和所下限,并且与维特比译码中的累积平方欧几里得距离类似。利用支路度量和路径度量对网络进行研究分析,在双向中继通信系统中,并且兼顾了实施复杂度和内存要求的同时,提出了一种新型的信息交互模型,实现了接近最优的中断性能。
1 系统模型
一个通信网络中的通信双方进行信息交互时,建立如图1所示的双向通信模型。这个模型被广泛使用于多跳中继及路径的选择,如在文献[11-12]中,A,B为2个信息发送源;Ci,(i=1,…,2M+1)为中继簇,其中每簇中继包含N个中继,第i簇的第j个中继用Rij表示。由于是双向传输模型,所以第i跳表示第i簇和第2M+2-i簇中继的传输。假设每一簇中继仅能和与之相邻簇内的中继进行通信。
这里用ei,j(m),m=1,2,…,2M+2,表示第m-1簇的中继i到第m簇的中继j的支路。多跳传输路径可以用一串支路表示为:
e1,i1(1),ei1,i2(2),…,ei2M+1,1(2M+2),
(1)
式中,in∈(1,2,…,Nn),n=1,2,…,2M+1。支路ei,j(m)的信道系数用hi,j(m)表示,假设为瑞利衰落。瞬时信噪比为:
(2)
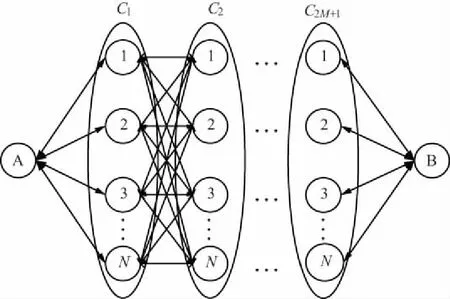
图1 双向多跳中继通信网络模型
2 BRSVA多跳中继选择算法
2.1 BRSVA算法描述
在传统的维特比算法(Viterbi Algorithm,VA)中,支路度量(Branch Metric,BM)定义为在时刻t输出符号与输入符号的欧几里得距离:
vt=‖yt-xt‖2。
(3)
它的路径度量(Path Metric,PM)如式(4)所示[13]。
ut=ut-1+vt。
(4)
维特比算法是一种找出最小PM,即最小累积欧几里得距离的有效方法,因为在时刻t-1时,仅储存最小PM路径,而其他所有路径将被摒弃。
本文提出了一种基于维特比算法双向多跳中继选择算法。不同于传统的维特比算法,定义第m-1簇的中继i与第m簇的中继j的BM为第m-1簇的中继i与第m簇的中继j的支路瞬时信噪比,记为γi,j(m),其PM为路径e1,i1(1),ei1,i2(2),…,eiL-1,1(L)的所有BM的最小值。为了减小复杂度,构建滑窗,在每个节点仅储存w个PM和BM。总的编码内存仍设为K,卷积码的输入k=K,并且有
(5)
当内存充满,滑窗内第一簇的某个中继将被选中,被选中的中继满足具有最小PM的最佳路径的条件,并摒弃掉所有其他路径,即可保证最后得到的幸存路径具有最大的等效信噪比。
滑窗内的支路度量BM和路径度量PM会被储存。当滑窗内存充满后,窗内第一簇中继中的最佳中继被选中。一条支路ei,j(m)的BM为这个支路的瞬时信噪比,一条多跳路径的PM为这条路径中所有支路度量的最小值,那么第n簇中继Rj的PM可表示为:
PM(Rj,n)=min{γi,j(1),…,γi,j(n)},
(6)
式中,n为这条路径所包含的跳数;i为当前跳发送端的簇数,A端为0,B端为2M+2;j为当前跳接收端的中继。
由于是双向传输,所以从A,B两端同时并行进行选择。记m-1为滑窗开始时的跳数,记q为滑窗内的当前跳数。从第一跳(m=1,q=1)开始,计算A与C1簇、B与C2M+1簇中每个中继的支路度量BM:
BM(R1,j,1)=γ0,j(1),
(7)
BM(R2M+2,j,1)=γ2M+2,j(1)。
(8)
存储BM(R1,j,1)中的最小值和BM(R2M+2,j,1)中的最小值记为当前跳的路径度量PM。
继而q+1,分别计算两端进入第m+q-1簇和第 (2M+2)-(m+q-1)簇中每个节点的所有路径的PM,即之前簇的幸存路径的PM值和当前跳的BM值中的最小值:
PM (Rj,m+q-1)=
min{PM(Ri,m+q-2),γi,j(m+q-1)},
PM(Rj,(2M+2)-(m+q-1))=
min{PM(Ri,(2M+2)-(m+q-1)),
γi,j((2M+2)-(m+q-1))}。
(9)
第m+q-1簇和第(2M+2)-(m+q-1)簇中每个节点存储具有最大PM值的路径,并摒弃其他所有路径。继续增加q重复以上步骤直到q=w。此时,窗内具有最大PM值的路径的第一个中继被选择为当前窗首跳的最佳中继。
滑窗向前滑进一跳,m+1,q=1。计算前一跳所选中继到当前窗内第一簇中所有节点的PM值,并重复上述步骤,直到m=M,即最中间跳,此时所有簇的中继选择完毕,进行下行链路的数据转发。
BRSVA算法流程如图2所示。
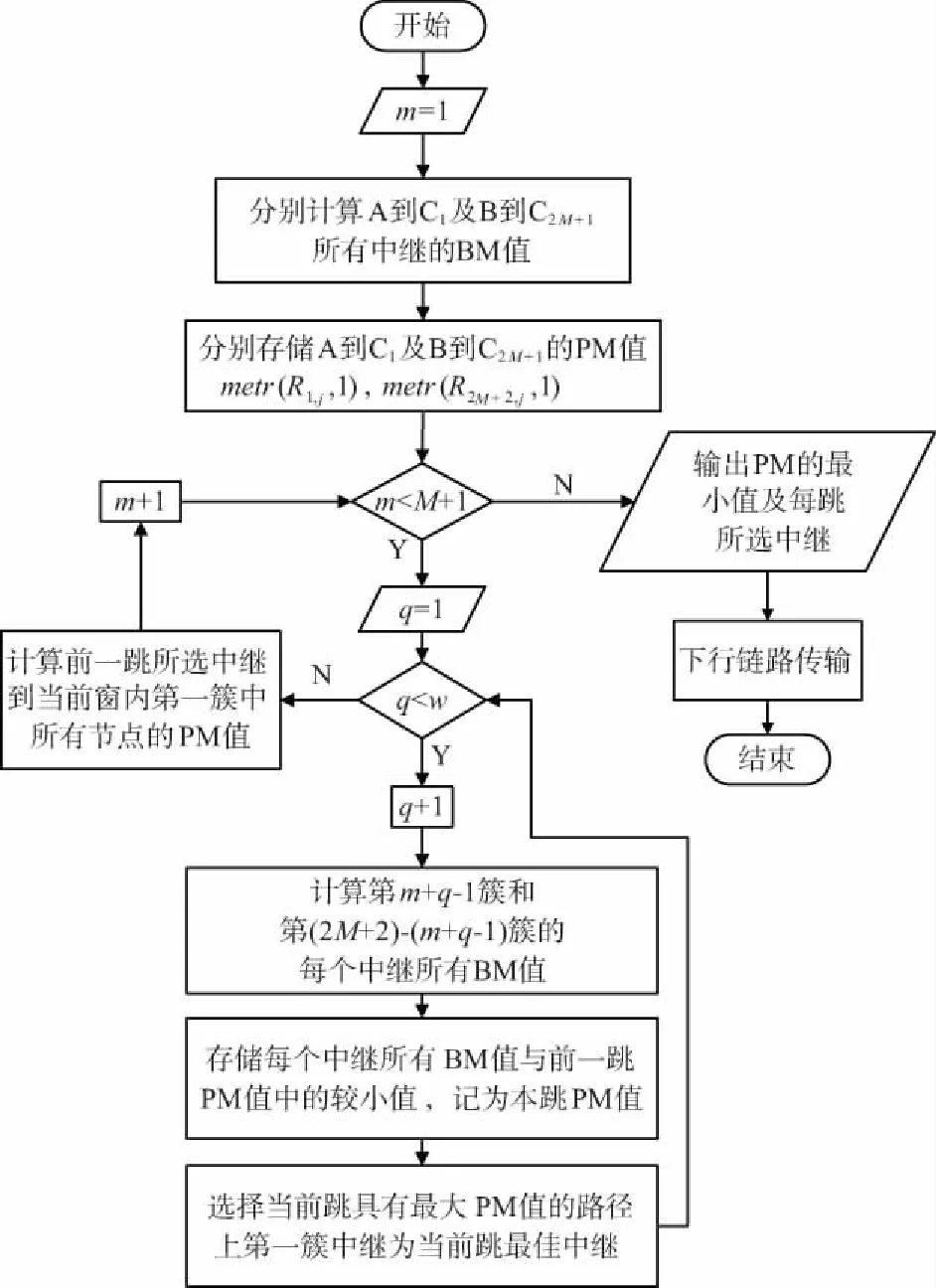
图2 BRSVA算法流程
上述BRSVA中继选择算法可通过采用集中式或分布式方法进行实施。如果采用集中式方法,那么需要一个中心控制器,可收集所有幸存路径的PM,并在内存充满时进行窗内第一簇最佳中继的选择。如果采用分布式方法,可在每个中继处加入基于瞬时信道状态的定时器,最佳中继的定时器倒计时将先于其他中继结束,并开始数据传输。在BRSVA算法中,滑窗内的第一簇中继选择可采用与此类似的方式。当内存充满后,滑窗内最后一簇的每个中继计算其PM,然后设置一个定时器,定时值与PM值成负相关,PM值越高,时间越短。通过这种方法,滑窗内具有最优路径的中继首先倒计时结束,然后它广播一个标志信号和它所选择的之前跳中继的身份信息。窗内最后一簇中的所有其他中继,在等待自身定时器归零的同时一直监听着周围的情况,一旦监测到其他中继所广播的标志信号,便停止自身计时并保持静默。当之前跳的中继监听到标志信号和身份信息后,马上检测此身份信息,如果与自身不吻合,便保持静默。倒数第二跳的所选中继再继续广播其所选择的前一跳中继的身份信息。这个过程一直进行到滑窗中的第一跳中继接收到身份信息,即窗内每一簇都完成了选择。最后,窗内第一簇的最佳中继发送一个完成选择信号,滑窗便向前移动一跳,并重复进行以上过程。
2.2 双向中继网络信息交互传输模型
通过BRSVA算法选出每一簇的最佳中继后,采用下述双向多跳中继信息交互的传输模型进行信息传输。如图3所示,假设Vi表示第Ci簇的被选最佳中继,那么VM+1表示最中间簇的被选中继。定义由A,B端向VM+1传输信息的链路为上行链路,由VM+1向A,B端传输信息的链路为下行链路。此处以M=2为例进行分析。
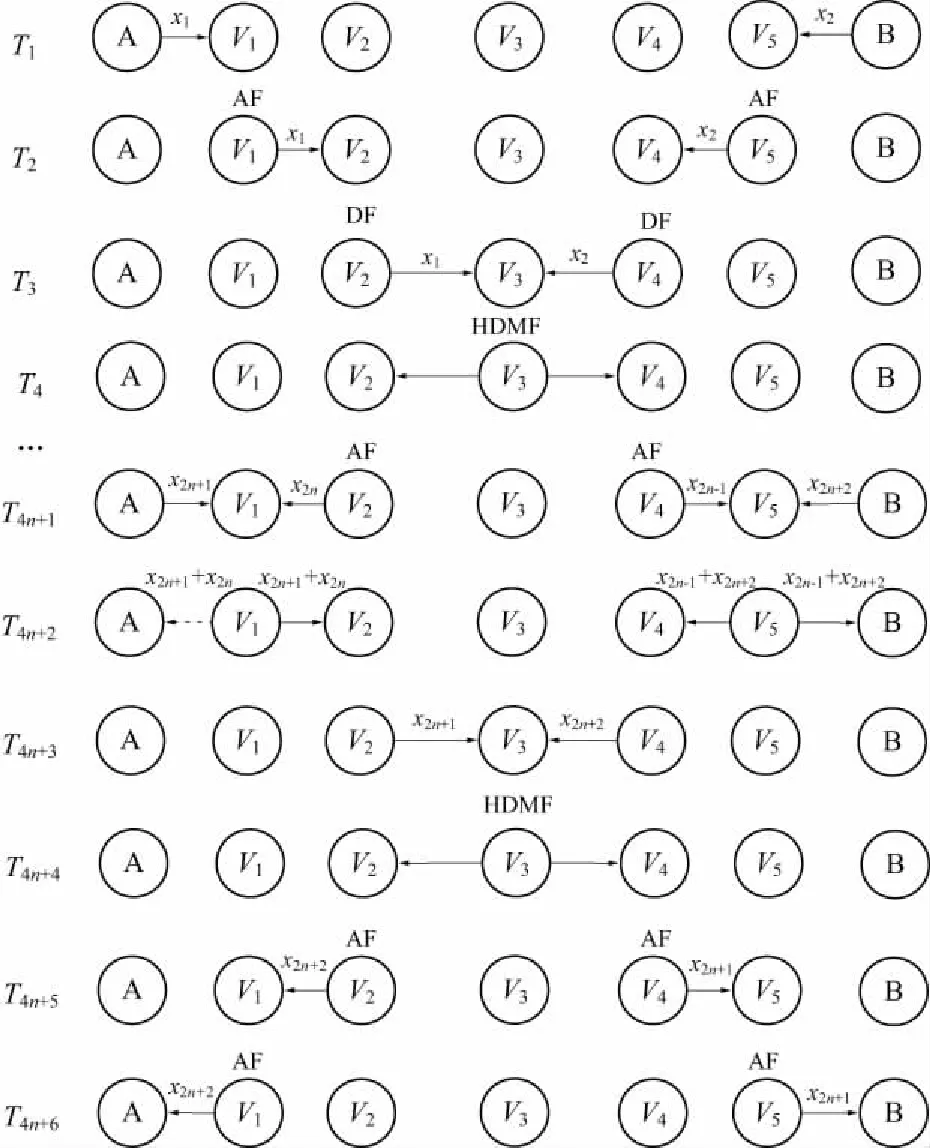
图3 双向多跳中继网络信息交互传输模型
信息交互模式可描述如下:在上行链路,T1时刻A和B分别向V1和V5发送数据x1和x2,记为第1跳;V1和V5收到数据后,在T2采用AF转发协议分别向V2和V4传输数据,记为第2跳;V2和V4接收到数据后,采用DF协议,对接收信号进行解码恢复出原始数据,再在T3发给V3,记为第3跳。而V3接收到数据后,采用HDMF[14]协议,判决采取直接DMF或是差分DMF协议。在T4n+1时刻,A继续发送x2n+1,B继续发送x2n+2。在下行链路,V3如果采取差分DMF协议,则在T4n+4时刻向V2和V4发送差分信号,而在T4n+5时刻,V2和V4分别采取AF协议分别向V1和V5转发信息,在T4n+6时刻,V1和V5分别向A,B转发信息;如果采取直接DMF协议,则信道较优的那路信息被传输给下一个节点,采取AF协议,直至A或B。
2.3 中断概率
系统的中断概率定义为:当所有支路中任一条支路的瞬时信噪比小于某阈值γth时,传输中断。根据上述讨论,可以表达为所有BM值中的最小值,也就是路径的PM值小于阈值γth时发生中断,
(10)
3 仿真结果分析
为了验证BRSVA算法的性能,进行了仿真实验。采用BPSK调制方式,信噪比阈值预设为γth=1dB。同时,给出了最优选择[17-18]的性能仿真,即w=+∞下的仿真作为参照,这种情况搜寻了所有可能的路径,为可达性能的上限。
6跳(M=2)的中继网络中BRSVA算法的中断概率性能如图4所示,其中每簇含2个中继。滑窗大小为w=1,w=2,w=5,K=k=1。可以看出,随着滑窗大小的增加,系统的中断性能随之提高。相比于最优选择,当中断概率为10-2,滑窗大小分别为w=1,w=2时,信噪比损失分别为7 dB和2 dB。当滑窗大小增至w=5时,BRSVA的性能可接近最优选择,此时信噪比损失可忽略,表明在有限的内存需求和实施复杂度下,BRSVA具有可行性。
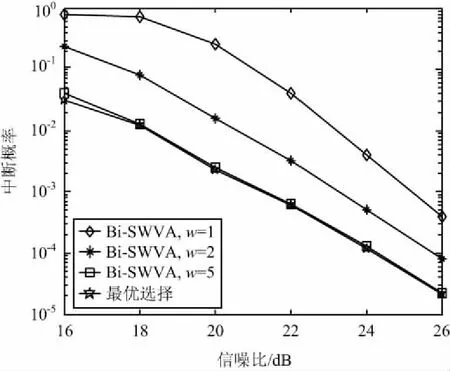
图4 M=2时中断概率变化曲线
总跳数为12跳,即M=5的网络下,中断概率随信噪比的变化曲线如图5所示,其中每簇中继数量为2~4的随机分布,K=k=5。相比于最优选择,当中断概率为10-3,滑窗大小分别为w=1,w=2时的信噪比损失分别为6 dB和1 dB。当滑窗大小增至w=10时,BRSVA的性能已接近最优选择,信噪比损失可忽略。

图5 M=5时中断概率变化曲线
4 结束语
本文研究了在双向多跳中继通信系统中,基于维特比译码的BRSVA中继选择算法,进一步提出了一种双向多跳传输模式下的信息交互模型,在有限的内存消耗下,可提高多跳中继通信网络的稳定性,降低系统的中断概率。
但是,本文仅考虑信道为瑞利衰落的条件,并未考虑各中继节点间信道状态不同的情况,以及信道衰落及其严重的情况,此处有待进一步研究。
