步进频信号慢速小目标长时间积累检测技术

原浩娟，史云鹏，高毓泽

(上海航天电子技术研究所，上海 201109)

0 引言

现代战争中，随着隐身飞机、巡航导弹和无人机突防等技术的出现，对雷达探测带来了极大的挑战。特别是对于低、慢、小目标，由于飞行高度低，速度慢，反射面小，容易被杂波覆盖，通常难以实现检测和稳定跟踪。步进频信号不仅能够防止杂波混叠，还能够以较小的时宽和瞬时带宽实现高分辨率，同时通过对慢速目标的长时间积累，能够有效提高系统的相参积累增益，有利于“低慢小”目标的长时间积累检测。

步进频信号作为一种合成宽带信号，具有瞬时带宽低、合成带宽高和易于实现等优点[1-3]，有利于实现小型防空系统的低成本设计，用于探测和跟踪无人机群等“低慢小”目标。采用多帧步进频信号联合处理，可以运动目标实现距离-速度的二维高分辨成像，并且能够进行长时间相参积累，有利于微弱目标的检测。同时，步进频信号可以有效防止杂波混叠，并且能够通过多普勒信息实现运动目标和杂波的分离，改善目标的信杂比[4]，有利于杂波中微弱目标的检测。

在长时间积累的过程中，由于步进频信号本身就是一种多普勒敏感信号，如何进行运动补偿，显得尤为关键。文献[5-12]提出了一系列步进频信号速度估计和运动补偿方法，但通常对回波信噪比有较高的要求。

本文采用先对多帧步进频信号的同频点测速，然后在对应的多普勒通道上测距的方法实现距离-多普勒二维高分辨成像。针对不同频点之间多普勒频谱展宽引起成像结果波形发散的问题，分别提出了时域重采样、频域重采样和多普勒通道对齐3种速度补偿方法，针对频域重采样和多普勒通道对齐方法成像结果旁瓣性能较差的问题，提出了利用补零内插进行改进的方法，并对3种方法的运算量及补偿性能进行了详细的分析和比较，从理论上将文献[13]介绍的Keystone算法在步进频领域得以应用，并创新性地将其在频域加以应用，有效提高了算法的实现效率，能够在没有速度先验信息的条件下同时实现步进频信号测距和测速，有效提高了工程可应用性，最大限度地发挥了其大时宽带宽积的优势，可以应用于“低慢小”目标的探测。

1 信号处理原理及问题分析

假设一帧步进频信号的步进点数为N，将M帧信号作为一个处理周期，则一个处理周期的步进频发射信号表达式为：

(1)

式中，Tr为步进频信号的脉冲重复周期；τ为子脉冲宽度；fn为子脉冲频率。在式(1)所示的发射信号中，令tm=m·NTr，称为“帧时间”，令tn=nTr，称为“脉冲时间”。假设目标在一个处理周期中保持匀速运动，则距离为R0处速度为v的点目标，在第m个步进帧的第n个脉冲重复周期中的距离，可表示为R(m，n)=R0-v·(tm+tn)，对应的回波时延τ(m，n)=2R(m，n)/c，对混频后的回波信号采样，并将同距离单元的采样结果记录在一个M×N的回波响应矩阵x中，可得

x(m，n)=Aexp(-j2πfnτ(m，n))，

(2)

式中，m=0，1，...M-1；n=0，1，...N-1；A为回波幅度。整理式(2)并归一化，可得

(3)

根据时域采样间隔及物理含义的不同，可将式(3)分为2部分：

(4)

(5)

式中，x1(m，n)仅与帧时间tm有关，相当于载频为fn，脉冲重复周期为NTr的脉冲多普勒信号对速度为v的目标的回波采样结果；x2(n)仅与脉冲时间tn有关，是一帧步进频信号对R0处速度为v的目标的回波采样结果。

对回波响应矩阵x的同频点维做DFT，步进频维做IDFT，可以得到运动目标的距离-多普勒像，即

(6)

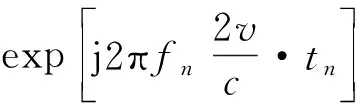
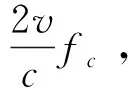
(7)

故整个步进频信号带宽内的多普勒频谱展宽程度可表示为：

(8)

如不进行补偿，就会影响其后的IFFT成像效果，造成目标像波形发散，峰值降低，影响雷达的分辨及检测性能。

通过上述分析不难发现，在多帧步进频信号成像过程中，需要的运动补偿包括2部分：一是目标运动在步进频帧内产生的耦合时移的补偿；二是不同频点之间多普勒频差的补偿。下面将对这2部分的补偿方法分别进行讨论。

2 速度补偿

为了便于分析，这里引入相对多普勒的概念[7]。定义相对多普勒频率为：

(9)

相对多普勒频率只与目标速度有关，不再受信号载频的影响。将式(9)分别代入式(4)和式(5)，可得

x1(m，n)=exp[j2πfnδ·tm]，

(10)

x2(n)=exp[-j2πfn(τ0-δ·tn)]，

(11)

式中，τ0=2R0/c。不难发现，在相对多普勒频率一定的条件下，式(10)和式(11)中的耦合相位项分别可以看成是子脉冲频率fn对tm和tn调制的结果，下面将详细讨论对这2个耦合相位项的补偿方法。

2.1 时域重采样法

帧时间tm的采样间隔为ts=NTr，对回波响应矩阵在帧时间域重采样，重采样时间间隔为：

(12)

将式(12)代入式(10)，可以得到重采样后的回波信号表达式：

(13)

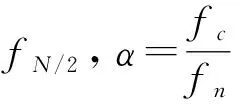
时域的重采样实际上是文献[3]中提出的keystone方法在步进频中的应用。文献[8]给出了sinc内插的实现过程，即

(14)

式中，mk=0，1，...M-1。

2.2 频域重采样法

对式(10)做M点DFT，可以将同频点数据转化到多普勒频域，有

(15)

由式(15)可以看出，DFT之后，目标在不同频点对应的多普勒谱线位置kn是受子脉冲频率fn影响的，需要进行补偿。

由于一个处理周期的积累时间为MNTr，DFT之后，对应的多普勒频域采样间隔为：

(16)

为了消除子脉冲频率对测速结果的影响，对式(15)所示的频域数据重采样，也即令

(17)

可得

(18)

容易发现式(17)所示的重采样过程与式(12)是一致的。由式(18)可以看出，频域重采样后，目标峰值位置不再受子脉冲频率影响，而仅与速度有关，多普勒频谱展宽得到补偿。频域重采样的扩展因子可以表示为1/α。

由于对回波响应矩阵做DFT时未做任何补偿，DFT之后不同频点的频谱泄漏情况不同，会影响频域重采样之后的成像效果，因此频域重采样之前需要首先补偿不同频点之间的频谱泄露效应，这可以通过对DFT前的原始数据一倍补零实现。补零进一步增加了内插所需的运算量，但是当运动目标的多普勒频率范围只占无模糊多普勒的一小部分时，可以仅对可能存在目标的那一部分数据进行补偿，这是时域重采样无法实现的；另外，由于补零减小了频谱泄露，频域重采样可以取得比时域重采样更好的补偿效果。

2.3 多普勒通道对齐法

kn=fnδMNTr+Δ1，

(19)

(20)

(21)

(22)

式中，round(·)表示四舍五入。数据重组的过程可以表示为：

(23)

(24)

因此，式(23)所示的数据重组过程，会在新的坐标位置引入一个线性相位，大小如式(24)所示，需要进行补偿，否则会影响其后的IDFT处理。以频点f0对应数据的相位为参考，补偿相位可以表示为：

(25)

由式(19)可得：

(26)

整理可得第n个频点的补偿相位可近似表示为：

(27)

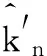
然而，由于通道量化误差的存在，式(27)所示的补偿相位存在补偿误差：

(28)

这一误差会抬高IDFT之后的距离旁瓣，影响最终的成像效果。对同频点数据做补零内插，可以使多普勒谱线细化，有效降低多普勒通道对齐方法中的补偿误差。可以证明，对数据做L倍补零内插，对应的补偿相位误差变为：

(29)

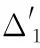
补零内插的另一个优点是会减小DFT时频谱泄漏引起的幅度损失，更有利于保存回波能量，这在微弱目标的检测中是很重要的。内插的缺点是会增加系统的计算量和存储量，但是由于补零内插可以在DFT处理中通过快速算法实现，与sinc内插相比，运算量仍然要小得多；另外，实际应用中，可以将内插倍数(运算量/存储量)与补偿效果进行折衷，是一种灵活的算法。

2.4 步进频耦合时移补偿

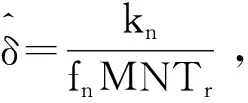
(30)

对经过多普勒频谱展宽补偿之后的数据矩阵做式(30)所示的相位补偿后再做IDFT，就可以消除耦合时移的影响，得到运动目标的距离-多普勒二维高分辨像。

3 性能分析及仿真

3.1 算法性能分析

主要讨论用于补偿多普勒频谱展宽的3种算法的补偿性能及运算量。其中，时域重采样法通过sinc内插实现了时域的重采样，有效地补偿了多普勒频谱展宽的问题，但是频谱泄露情况没有得到改善；频域重采样法在补偿多普勒频谱展宽的同时，通过对原始数据补零有效地减小了频谱泄露的影响，补偿效果要优于时域重采样；而多普勒通道对齐法由于相位补偿误差的存在，补偿效果较差，但通过补零内插可以大大改善补偿效果，并减小频谱泄露。表1对3种方法的补偿性能进行了比较，并对补偿一个距离单元的回波响应矩阵所需的运算量进行了估算。其中K=2Nfdmax/PRF，表示目标多普勒范围与无模糊多普勒的比值，fdmax为目标最大多普勒频率[14-16]。

表1 算法性能比较

补偿方法运算量补偿效果时域重采样M2N次乘加多普勒频谱展宽得到了补偿,但是存在频谱泄露频域重采样2M 2N/K次乘加多普勒频谱展宽及频谱泄露均得到了补偿多普勒通道对齐MN/K次复乘由于相位补偿误差的存在,会抬高旁瓣,通过补零内插可以大大改善补偿效果

3.2 算法仿真

通过仿真比较时域重采样、频域重采样以及多普勒通道对齐法的补偿性能。仿真参数如下：f0=10 GHz，Δf=80 MHz，τ=3 μs，N=16，M=64，PRF=83.3 kHz，R0=1 700 m，v=29 m/s。图1(a)为未经速度补偿的DFT结果以及距离-多普勒像，可以看出处理结果的波形严重发散，目标难以检测；图1(b)、图1(c)和图1(d)分别为时域重采样、频域重采样和多普勒通道对齐法的补偿效果。可以看出时域重采样和频域重采样均有较为理想的补偿效果，多普勒通道对齐法则出现了较高的旁瓣。图2则对上述几种补偿方法的一维距离像进行了比较，可以看出频域重采样方法和内插后的多普勒通道对齐方法由于补偿了频谱泄露效应，目标幅度要高于其他目标像，同时内插后的多普勒通道对齐方法与内插前相比，旁瓣性能有了很大的改善[17-19]。

图1 成像结果对比

图2 不同速度补偿方法一维距离像比较

4 结束语

针对多帧步进频信号成像过程中多普勒频谱展宽的问题，提出了3种补偿方法：时域重采样法、频域重采样法和多普勒通道对齐法。其中，时域重采样法通过对帧时间域的重采样补偿不同载频之间多普勒频率不一致的问题；频域重采样法通过对多普勒频域重采样实现不同频点之间多普勒频差的补偿；时域重采样和频域重采样均采用sinc内插实现，运算量大；多普勒通道对齐法利用多普勒频域的数据重组取代sinc内插，有效降低了运算量，易于实现；另外，还通过分多普勒通道补偿的方法，有效地补偿了目标运动在步进帧内产生的耦合相位项，进一步提高了成像质量。最后需要指出的是，提出的速度补偿方法不仅适用于步进频信号，也同样适用于其他频率编码信号。