Reed-Solomon码性能增强译码算法

郑相全，段 文

(1.军事科学院 系统工程研究院，北京 100141；2.北京直属保障大队，北京 100071)

0 引言

自1960年Reed-Solomon(RS)码[1]被构造后，由于其突出的抗突发性能，已被广泛应用于通信系统中，包括数字存储、卫星和深空空间通信，移动数据通信和扩频系统。1961年Gorenstein和Zierler证明了RS码是非二进制BCH码的子类[2]。因此，RS码编码有按BCH码编码方式和RS码定义方式2种编码结构[3]，其中BCH码编码方式可以构造RS系统码格式[4]。

已经提出的RS译码算法主要是基于信道输出硬判决信息的BM算法和欧几里德算法[5]。这些传统的RS码译码算法利用了编码时所依附有限域的代数结构来进行译码，所以又称为代数译码。(n，k)RS码采用代数译码方法进行译码时，会有纠错能力的限制。本文首先从RS码的2种编码格式出发，介绍了突破RS码设计纠错能力的2类译码增强算法，最后总结了这2类算法存在的问题并指出了其后续的研究方向。

1 RS码编码格式分类

1.1 计算映射RS码定义格式

RS码是采用编码方式为计算映射编码[1]，这种编码方式是后续GSA[6]和KVA[7]算法的基础。

设信息多项式为：

m(x)=mk-1xk-1+mk-2xk-2+…+m1x1+m0。

(1)

设支撑集D={x1，x2，…，xn}∈GF(2m)，为两两互异的一个点集；则RS码的码字可由变量x遍历支撑集内的值，依次代入消息符号多项式进行计算得到[8]，

c=(m(x1)，m(x2)，…，m(xn))，

(2)

因此，

m·G，

(3)

式中，

(4)

为k列n行的范德蒙矩阵[9]。显然，RS码的码长由支撑集的阶数决定。

设α为RS码符号域GF(2m)的一个本原元，则符号域GF(2m)中的一种排序为：(0，1，α，α2，…，αn-2)，其中n=2m为符号域的阶数。若按顺序依次取符号域内所有非零元素构成的集合D={1，α，α2，…，αn-2}时，生成矩阵为：

(5)

假设接收的硬判决码字序列为：

r=(rn-1，rn-2，…，r0)。

在接收端，可构造n个方程组。若信道无差错时，该方程组为：

假设取上述方程组的前k个方程，对应的系数行列式为：

即上述方程组的任意k个方程是相互独立的，即假设信道无差错传输时，上述的任意k个方程组即可求解出发送的码元信息序列。

1.2 RS码的系统码编码格式

由于RS码为最小距离可分的[10]，因此参数为(n，k)的RS码的最小汉明距离dmin=n-k+1。作为BCH码的子类，可得RS码的生成多项式为：

g(x)= (x-α)(x-α2)…(x-αdmin-1)=

gn-kxn-k+gn-k-1xn-k-1+…+g1x+g0，

(6)

式中，α为RS编/译码符号域GF(q)内的本原元。由生成多项式可得k个相互独立的码字多项式：

因此，RS码的一个生成矩阵为：

(7)

设信息符号序列m=(mk-1，mk-2，…，m1，m0)，为一行向量，其作为系数对应的信息多项式为m(x)=mk-1xk-1+mk-2xk-2+…+m1x1+m0。

设码字符号序列c=(cn-1，cn-2，…，c1，c0)，其作为系数对应的码字多项式为C(x)=cn-1xn-1+cn-2xn-2+…+c1x1+c0。因此码字序列可生成

c=m·G。

(8)

对生成矩阵进行行列式变换，可得下列标准矩阵形式：

G=[IkP]，

(9)

式中，Ik为k×k单位矩阵；基于标准生成矩阵，可得系统RS码的码字多项式为：

C(x)=m(x)xn-k+p(x)，

(10)

p(x)为系数取自校验序列的校验多项式。

由定义可知，每个BCH码类的码字都可被其生成多项式g(x)整除，由式(10)可得：

p(x)=C(x)+m(x)xn-k≡m(x)xn-kmodg(x)，

(11)

因此，RS码字多项式可表示为：

C(x)=m(x)xn-k+p(x)≡m(x)xn-k+

在对断路器的处理中，在一些特殊的情况下会采取就地操作的形式完成相应的动作。但在实际应用中，我们会经常发现在进行就地电动操作时，机构的动作经常会出现错误，或机构不动作[5]。在发生这种情况时，首先要对电源的操作情况进行检查，确保其处于正常状态。其次对机构分、合闸线圈进行减压，如果是因线圈烧毁引起的机构错误动作或不动作，则应当对线圈进行更换，在对线圈的阻止大小进行对比时，要对操作电流的是交流电还是直流电进行区分。

m(x)xn-kmodg(x)。

(12)

2 基于多项式插值的列表译码算法

传统的RS码译码算法利用编码时所依附有限域的代数结构来进行译码，所以又称为代数译码。(n，k)RS码采用传统代数译码方法进行译码时，其纠错能力为t=(dmin-1)/2，其中dmin=n-k+1为码字的最小距离。

1997年Guruswami和Sudan[11]指出突破RS码的纠错能力限是可能的。Guruswami-Sudan(GS)算法的纠错能力已突破传统代数的纠错能力t，其纠错能力可达：

(13)

GS算法的主要思路是利用多项式插值方法，将接收到的序列通过多项式插值的方法重构生成多项式。

Koetter-Vardy(KV)算法在GS算法的基础上，依据信道输出的每个软信息，给出了每个差值点不同的重数分配方法。总体上，KA算法主要分为5步：计算可靠性矩阵/Reliability Matrix；求重数矩阵/Multiplicity Matrix；Koetter-Vardy插值(软插值)；Roth-Ruckenstein多项式分解(求根)候选码字的选择输出。Koetter-Vardy Algorithm (KVA)流程如图1所示。

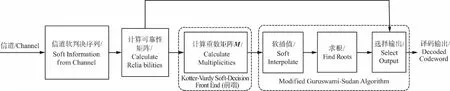
图1 Koetter-Vardy Algorithm (KVA)流程

3 基于信道软输出可信度的性能增强算法

虽然GS算法被广泛认为是能够突破RS码纠错能力的第一种译码算法，但是Forney在1966年提出的译码结构(不指定编码类型)以及Chase在1972年利用信道软输出提供的可靠性信息来产生比HDD译码算法更好的性能增强算法，该过程的纠错能力可以扩展到HDD译码算法的2倍[12-13]。

3.1 广义最小距离译码

广义最小距离(Generalized Minimum Distance，GMD)译码：对于最小汉明距离为dmin的(n，k)线性分组码，GMD译码算法基于纠错纠删代数译码算法，产生最多⎣(dmin+1)/2」个候选码字，最后从候选码字译码结果中选择最可能的一个作为译码输出[14]。若2v+e≤dmin-1，则纠错纠删译码算法可以纠正v个错误和e个删除的所有组合。GMD算法考虑e≤dmin-1个删除出现在dmin-1个最不可靠位置的所有情况，这些最不可靠位置为最可能出错的位置。

根据接收序列r得到硬判决接收序列RHD，并对RHD中的每一个符号分配一个可靠值；修正硬判决接收序列RHD，产生⎣(dmin+1)/2」个序列的列表。

若dmin为偶数，修正RHD的方法为：删除最不可靠的符号、删除最不可靠的3个符号、……、删除最不可靠的dmin-1个符号；若dmin为奇数，修正RHD的方法为：不删除任何符号、删除最不可靠的2个符号、……、删除最不可靠的dmin-1个符号。

使用纠错纠删代数译码算法对每一个修正后的候选码字进行译码。计算每一个候选译码码字的软判决译码度量，选择最可能的候选码字为译码结果。

3.2 Chase系列算法

作为GMD译码方法的推广，Chase发明了3种算法：Chase-III、Chase-II和Chase-I。

Chase-III：非常类似GMD算法，区别就在于修正硬判决信息时用取反操作代替了删除操作(即将1变为0，0变为1)，在译码时仅使用纠错的译码算法即可；具体方法不再赘述。对于二进制码，Chase-III算法和GMD译码算法的差错性能大致相同，所需的算法复杂度也大致相等。

Chase-II：是对Chase-III的一个改进，它产生一个用于译码的更大的候选码字列表。Chase-II算法中，局限在硬判决接收序列z的⎣dmin/2」个最不可靠位置上的所有可能错误组合组成的错误模式的集合E个被用来修正z。集合E称为测试错误模式集合(Test Error Pattern Set)，它由2⎣dmin/2」个测试错误模式组成，这些错误模式是考虑到z的⎣dmin/2」个最不可靠位置上0和1的所有组合而得到的。因此，Chase-II算法的候选码字的列表随最小距离dmin指数增长，这将有可能导致过多的计算空间和计算复杂度，不过Chase-II的差错性能要远胜Chase-III。

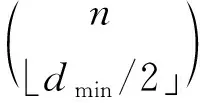
在3种Chase算法中，Chase-II在差错性能和译码复杂度上具有最优的平衡。RS码的Chase译码均指Chase-II译码结构。

列表辅助译码和有界距离译码之间关系的示意图如图2所示。假设应判决的接收向量为r，在有界译码算法中，当硬判决的接收向量r落入某码字c0的汉明球内，有界距离译码算法译接收向量r为码字c0，此时distance(c0，r)≤dmin/2；当接收向量r没有落入任一个码字所在的汉明球内，如图2(b)所示，此时有界距离算法译码失败；在Chase辅助译码中，对于图2 (b)情形，通过对接收向量r的若干个最不可靠比特位进行翻转，“辅助”修正后的接收向量r′进入到某个码字的汉明球内，如图2(c)所示。显然对于有限距离无法译码的码字，可以通过不可靠位的辅助修正，可能会被纠正过来，从而突破有限距离译码的纠错能力。

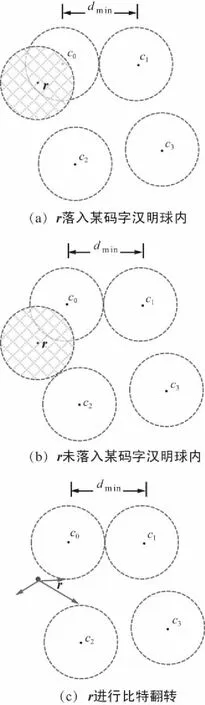
图2 RS码有界距离译码算法

以(255，239)RS 码为例，对上面算法的误帧率性能进行了比较，具体的仿真参数如表1所示。(255，239)RS码的不同译码算法误帧率性能对比如图3所示。

表1 RS码硬判决译码算法纠错能力对比及示例

参量参量值(255,239)RS码码符号长度n=2m-1255信息符号个数k239校验符号个数r=n-k=2t16最小码距(符号)dmin=2t+117符号域GF(2m)GF(256)BMA纠错能力dmin-1 /28GS纠错能力n-n-dmin n8.647RS码Chase译码纠错能力(最大)2t16

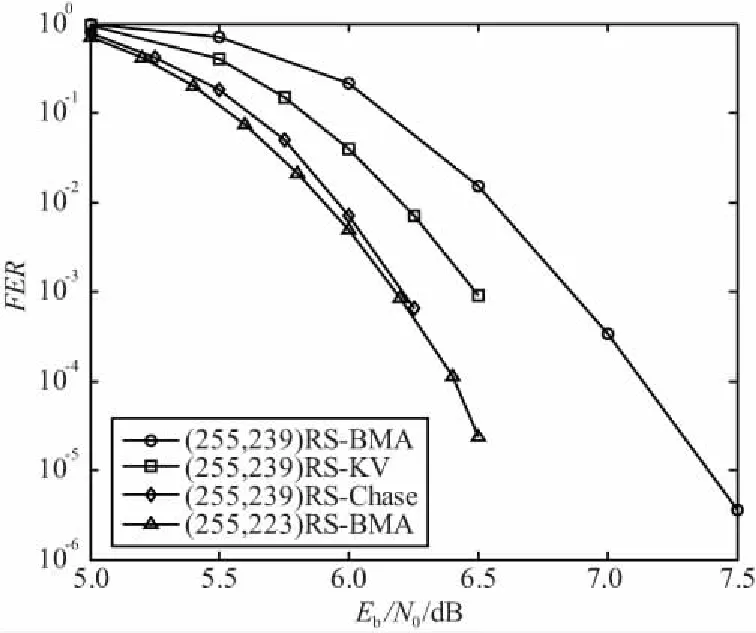
图3 (255，239)RS码的不同译码算法误帧率性能对比

从图3的(255，239)RS码误帧率性能可以看出，相对于传统的BMA译码算法，KV算法可以提升RS码的性能，在误帧率为10-3时，大约有0.35 dB的性能增益；但此时RS码的Chase译码算法有大约0.65 dB的增益，接近汉明距离大1倍的 (255，223)RS码的BMA算法的性能，这和前面的分析是一致的。

4 结束语

Chase列表译码算法的性能随着不可靠位的增大而增强，最大可扩展到其设计纠错能力的2倍；然而Chase译码算法的复杂度随着最可靠位的位数呈指数级的增加。针对Chase译码复杂度高的问题，文献[15-16]分别利用多项式插值和Belief Propagation迭代算法的低复杂度的译码算法；文献[17]提出的概率生成候选测试向量的Chase译码算法，但是这些算法对dmin来讲，复杂度的改善还是非常有限的。寻找更低的低复杂度的Chase列表译码算法结构是后续研究的方向。