FEC design for remote control and data transmission of aeronautic and astronautic vehicles

Qin HUANG,Mingxu ZHANG,Zulin WANG,b,*,Xunwei ZHANG

aSchool of Electronic and Information Engineering,Beihang University,Beijing 100191,China

bCollaborative Innovation Center of Geospatial Technology,Wuhan 430079,China

KEYWORDS Circulant decomposition;FEC;High efficiency;LDPC;Nontransparent

Abstract This paper focuses on the advanced Forward Error Correction(FEC)based on Low-Density Parity-Check(LDPC)codes for remote control and data transmission of Aeronautic and Astronautic Vehicles(AAV).It shows that the nontransparent LDPC codes with odd row weights are able to resist phase inversion with a small computational overhead.To the best of our knowledge,it is the first time to use FEC to resist phase inversion.Then,a high hardware-efficient FEC design for AAV,which is capable of correcting random errors as well as phase inversion,is proposed based on circulant decomposition with circulant size of 2s.Such a(4096,2048)LDPC code has been adopted in a data transmission system due to its excellent error performance and hardware efficiency.

1.Introduction

Over the past few years,Aeronautic and Astronautic Vehicles(AAV)are developing and evolving rapidly.1-6Due to the dynamic of AAV,which changes the link geometry and multipath conditions,and the influence of atmosphere,the communication channel for remote control and data transmission of AAV is volatile,noisy and unreliable.Meanwhile,the resources that can be used for aeronautic and astronautic mission are extremely restricted by the payload capacity of AAV.Therefore,efficient and reliable remote control and data transmission of AAV are urgently required.

Forward Error Correction(FEC)is a technique used for controlling errors in data transmission over unreliable or noisy communication channels.The core idea is that the transmitted message is encoded in a redundant way by using an error correcting code.The redundancy allows the receiver to correct a certain number of errors.

It is very challenging to design FEC for remote control and data transmission of AAV.On one hand,the FEC must provide high coding gain to resist the thermal and phase noise caused by the channel.On the other hand,the FEC must be implemented efficiently because the resources of the aeronautic and astronautic mission are rather limited compared with the land-based mission.

In the past few decades,concatenated Reed-Solomon codes and convolutional codes are often used in aeronautic and astronautic mission.A(31,23)Reed-Solomon code concatenated with a rate 4/5 convolutional code is used in Link-16 communication.7And a(255,223)Reed-Solomon code concatenated with a rate 1/2 convolutional code is recommended by the Consultative Committee for Space Data Systems(CCSDS)for space data system.8Recently,Low-Density Parity-Check(LDPC)codes,a class of linear block codes,show near-capacity performance while implementable decoders are simultaneously admitted.9,10They outperform concatenated Reed-Solomon codes and convolutional codes by about 1-2 dB.Thus more and more astronautic missions consider LDPC codes as their FEC scheme.For instance,S.Lin designed an (8176,7156)quasicyclic Euclidean geometry LDPC code for NASA’s near-earth space mission.11Moreover,it is widely believed that LDPC codes have a great potential for aeronautic mission.

In order to efficiently keep the reliability of the remote control and data transmission of AAV,this paper presents an advanced FEC design based on LDPC codes.The advanced FEC design contains code construction as well as its codec implementation.We prove that an LDPC code is nontransparent if and only if its parity-check matrix contains at least one row with odd weight.The resulted nontransparent codes are resistant to the decoding failures caused by phase inversion of codeword in aeronautic and astronautic channel.And we construct the FEC codes based on circulant decomposition,which provides excellent error performance to resist noise and flexibility of circulant size and column weight.Analysis indicates that the design can be implemented with better performance and lower complexity than the(8176,7156)LDPC code adopted by NASA.Moreover,a data transmission system has adopted such a code as its standard code due to the excellent error performance and hardware efficiency.

The paper is organized as follows:In Section 2,we prepare the preliminary for the following contents.Section 3 studies nontransparent LDPC codes for AAV.The FEC design based on circulant decomposition is addressed for high performance and flexibility in Section 4.In Section 5,their implementation is provided,and finally conclusions and perspectives are drawn in Section 6.

2.Preliminary

An(n,k)LDPC code C is a linear block code given by the null space of anm×nparity-check matrix H that has a low density of 1 s.Lethi,j(1≤i≤m,1≤j≤n)denote the element in theith row andjth column of H.Letdc,i(1≤i≤m)denote the row weight of theith row of H.Let x=[x1,x2,...,xn]denote the codeword.The codeword x should be checked by each parity-check equation,i.e.,for theith parity-check equation,it must satisfy that:

Almost all LDPC code constructions keep the row-column constraint(RC constraint)on H:No two rows(or two columns)have more than one position in common that contains a nonzero element.

The original LDPC codes are randomly constructed based on computer search,such as Gallager codes,MacKay codes and Progressive-Edge-Growth (PEG)codes.Thus,their parity-check matrices possess little structure apart from being a linear code.9,12,13In this manner,it raises the complexity in both encoding and decoding.Quasi-Cyclic LDPC (QCLDPC)codes are a class of LDPC codes with tremendous structure, leading to simplified encoder and decoder designs.14-17The H matrix of a QC-LDPC code is generally represented as an array of circulants,i.e.,

whereAi,j(0≤i＜r,0≤j＜s)is az×zcirculant.A circulant is a square matrix such that every row is the cyclic-shift one place to the right of the row above it.

Finite geometries are powerful mathematical tools for algebraically constructing structured LDPC codes.18Euclidean geometry is a kind of finite geometries which can be used to construct QC-LDPC codes,called QC-EG-LDPC codes.Performance of QC-EG-LDPC code is close to the Shannon theoretical limit.One of QC-EG-LDPC codes has been used in NASA.11

Consider them-dimensional Euclidean geometry EG(m,q)over the Galois field GF(q).This geometry consists ofqmpoints andqm-1(qm-1)/(q-1)lines.A point in EG(m,q)can be represented as anm-tuple over GF(q).

The Galois field GF(qm)as an extension field of GF(q)is a realization of EG(m,q).Let α be a primitive element of GF(qm).Then the powers of α,

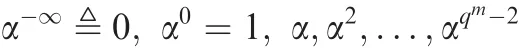
represent theqmpoints of EG(m,q),where α-∞represents the origin point of EG(m,q).

Let EG*(m,q)be a subgeometry of EG(m,q)obtained by removing the origin α-∞and all the lines passing through the origin from EG(m,q).This subgeometry consists ofqm-1 non-origin points and(qm-1-1)(qm-1)/(q-1)lines not passing through the origin.

Let L bealinein EG*(m,q)consisting of points

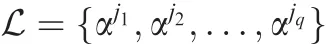
It is easy to prove that theqm-1 lines,L，αL，α2L，...，αqm-2L，form a cyclic class.All lines in EG*(m,q)can be partitioned into

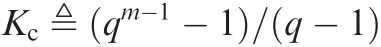
cyclic classes,denoted as S1，S2，...，SKc.

For any line L in EG*(m,q)not passing through the origin,the incidence vector of L is defined as the following(qm-1)-tuple over GF(2):

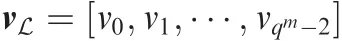
whose components correspond to theqm-1 non-origin points, α0，α，...，αqm-2,in EG*(m,q),wherevi=1 if αiis a point on L,otherwisevi=0.

Using the incidence vectors vL，vαL，vα2L，...，vαqm-2Lof the lines L，αL，α2L，...，αqm-2L in Sias rows arranged in right cyclic order,we can form a(qm-1)×(qm-1)circulant matrix Hc,iover GF(2)with both column and row weightsq.

For 1≤k≤Kc,we form the followingk(qm-1)×(qm-1)matrix over GF(2):

The subscript‘‘c” of HEG,c,kstands for ‘‘cyclic”.

Using the incidence vectors vL，vαL，vα2L，...，vαqm-2Lof the lines L，αL，α2L，...，αqm-2L in Sias columns arranged in downward cyclic order,we can form a(qm-1)×(qm-1)circulant matrix Gc,iover GF(2)with both column and row weightsq.

For 1≤k≤Kc,we form the following(qm-1)×k(qm-1)matrix over GF(2):

where the subscript‘‘qc” of HEG,qc,kstands for ‘‘quasi-cyclic”.HEG,qc,kdefines the null space of a QC-EG-LDPC code.

The(8176,7156)QC-LDPC codeC2designed by S.Lin for NASA is constructed based on the three-dimensional Euclidean geometry EG(3,23)over the field GF(23).There are 9 cyclic classes,S1,S2,...,S9.By splitting each column of Si,into 4 columns of the same length with its weight uniformly distributed into the 4 new columns,Sican be partitioned into four 511×511 circulants,Each circulanthas column and row weight of 2.Using these 4 circulants,a 511×2044 matrix is formed:

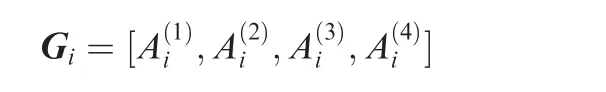
Then the parity-check matrix H2of C2is given below:

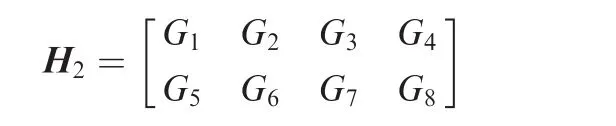
which defines the null space of the(8176,7156)QC-LDPC code C2.

3.Nontransparent LDPC codes for AAV

Many negative factors affect and limit possibilities of aeronautic and astronautic communication channel.Most of these factors cause two types of noise,the additive thermal noise and the multiplicative phase noise.While the additive thermal noise arises only from the receiver side of the communication system,the multiplicative phase noise is projected from the receiver side local oscillators as well as from the transmitter side carrier sources.To ensure a high correctness of decoding a codeword without phase inversion ambiguous for remote control and data transmission of AAV,a nontransparent LDPC code for AAV needs to be designed.

In general,the channel of satellite is Additive White Gaussian Noise(AWGN)model.19If the multipath effect is strong,the channel of airplane in flying communication with the ground station is Rician channel;otherwise,it can also be considered as AWGN.20Besides AWGN noise,the whole received symbols of a frame may be rotated π radians,which is called frame phase inversion,due to the combined effect of transmission phase disturbance and asynchrony of crystal oscillator.

The basic channel model of AAV for communicating with LDPC codes can be described as follows.

Ak-bit information sequence is encoded by an(n,k)binary LDPC code C,wherenrepresents the length of the codeword.The codeword is PSK modulated and the transmitted symbols are subjected to AWGN and phase inversion.LetPdenote the probability of frame phase inversion.Here assuming that the codeword is BPSK modulated,at the receiver after matched filtering and sampling,we have

wheresi∈{+1,-1}is theith transmitted symbol,riis theith received symbol,ηiis the AWGN noise andnis the number of transmitted symbols.

For the sake of simplicity,we focus on the above channel of AAV to describe and analyze our approach.

In general,the traditional approach with differential coding can resist phase inversion.But it needs 1-2 dB higher received signal-to-noise ratio to achieve the same error performance as that without differential coding.21So we propose the FEC approach without using differential coding which does not introduce any performance loss.Indeed,the proposed FEC approach takesPtimes decoding more than the traditional approach,wherePis the probability of frame phase inversion,e.g.,P=0.1 in Section 5.As a result,it provides a good tradeoff between complexity and performance for most applications.

The FEC can be separated into two classes in terms of frame phase inversion,transparent codes and nontransparent codes.If all valid codewords of an FEC code are still valid codewords after frame phase inversion,the code is called transparent code.On the contrary,if there exists a valid codeword of an FEC code which is not a valid codeword after frame phase inversion,the code is called nontransparent code.

A theorem for designing nontransparent LDPC codes is presented as follows.

Theorem 1.An LDPC code is nontransparent if and only if its parity-check matrix contains at least one row with odd row weight.

Proof.For an(n,k)LDPC code C,let xr=denote the symbols with phase inversion of codeword x=[x1,x2,...,xn].Any phase inversion of the symbol is equivalent tormodulo-2 addition of the symbol with element one,i.e.,xj=xj+1(mod 2).

⇐:In this direction,suppose H contains at least one row with odd row weight.Letdc,kbe odd.Using thek-th parity check equation to check xr=,the result is obvious as follows:

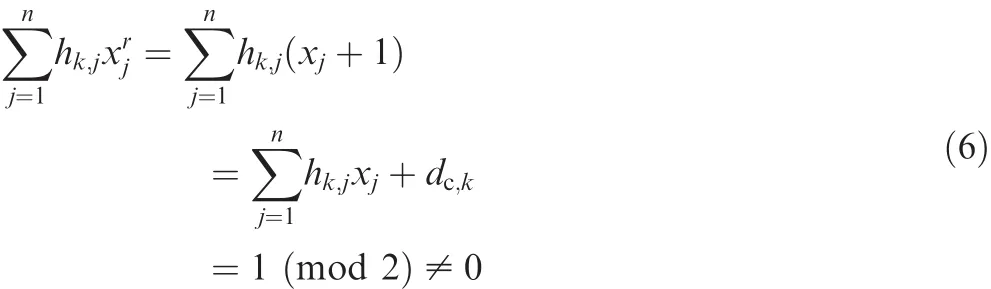
Thus xr=is not a valid codeword of C.Therefore,according to the definition of nontransparent codes,the LDPC code C is nontransparent.

⇒:Conversely,in this direction,suppose H contains no row with odd row weight,which meansdc,iis even for 1≤i≤m.Using anyith parity-check equation to check xr=...,xnr],the result is obvious as follows:

Thus xr=is still a valid codeword of C.Therefore,according to the definition of transparent codes,the LDPC code C is transparent.

Hence,an LDPC code is nontransparent if and only if its parity-check matrix contains at least one row with odd row weight.□

According to Theorem 1,QC-LDPC codes can be designed by properly selecting and masking circulants to make sure that some rows of parity-check matrix have odd row weight,which can guarantee the designed QC-LDPC codes to be nontransparent.

The proposed nontransparent QC-LDPC codes can efficiently solve decoding failures caused by frame phase inversion,whose simulation results are shown in Section 5.

4.FEC design based on circulant decomposition

Efficient and reliable remote control and data transmission of AAV are urgently required.The FEC design must provide high performance and low resource consumption.Nowadays,many QC-LDPC code designs are unable to provide flexible code length and rate to satisfy the demands of various missions.The size of a circulant in algebraic QC-LDPC code isqm-1.18,22,23Thus efficient Banyan network cannot be used to reduce the resource consumption.24Moreover,QC-LDPC codes like the NASA uses consist of circulants with column weight two,which raises the complexity of decoder.

Therefore,we propose the FEC design based on circulant decomposition.Particularly,we can use the proposed FEC design to construct a class of QC-LDPC codes with circulants of a size of 2sby circulant decomposition,called QC-CDLDPC codes.As a result,it can be implemented with a Banyan network to reduce resource consumption.24What’s more,our design can guarantee the column weight of circulant to be one,i.e.,the circulant is a cyclic-shift of an identity matrix.Thus,the complexity of decoder implementation can be significantly reduced.The FEC design based on circulant decomposition is shown as follows.

Firstly,the size of a circulant in QC-LDPC code should be determined and denoted as 2s.Secondly,aqneeds to be determined,which is subject toq2-1=(q+1)(q-1)=2s×c,wherecis a constant positive integer andqis a positive power of a prime.Thirdly,HEG,c,1can be constructed based on EG*(2,q):

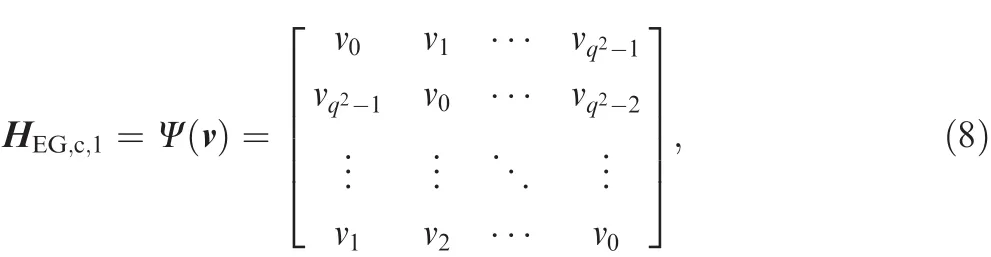
where HEG,c,1is a circulant.The generator of the circulant is its first row v=[v0,v1,...,vn-1].For simplicity,HEG,c,1is denoted by its generator as follows:HEG,c,1=Ψ(v)=Ψ(v0,v1,...,vn-1).From Eq.(8),we see that the rows and columns of HEG,c,1are labelled from 0 toq2-1.

Becauseq2-1=2s×c,we label the columns and rows of HEG,c,1from 0 toc×2s-1.Let I={0,1,2,...,c×2s-1}be the index set for the columns and rows of HEG,c,1.Define the following index sets:

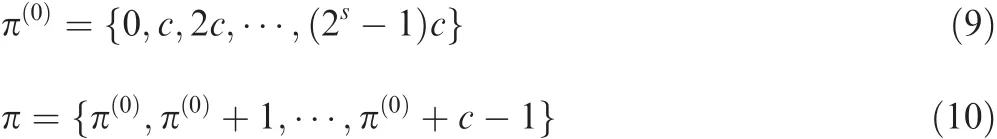
Then,π gives a permutation of the indices in I.Suppose that we first permute the columns and then the rows of HEG,c,1based on π,and these column and row permutations based on π result in the followingc×carray of circulants of size 2s×2sover GF(2):

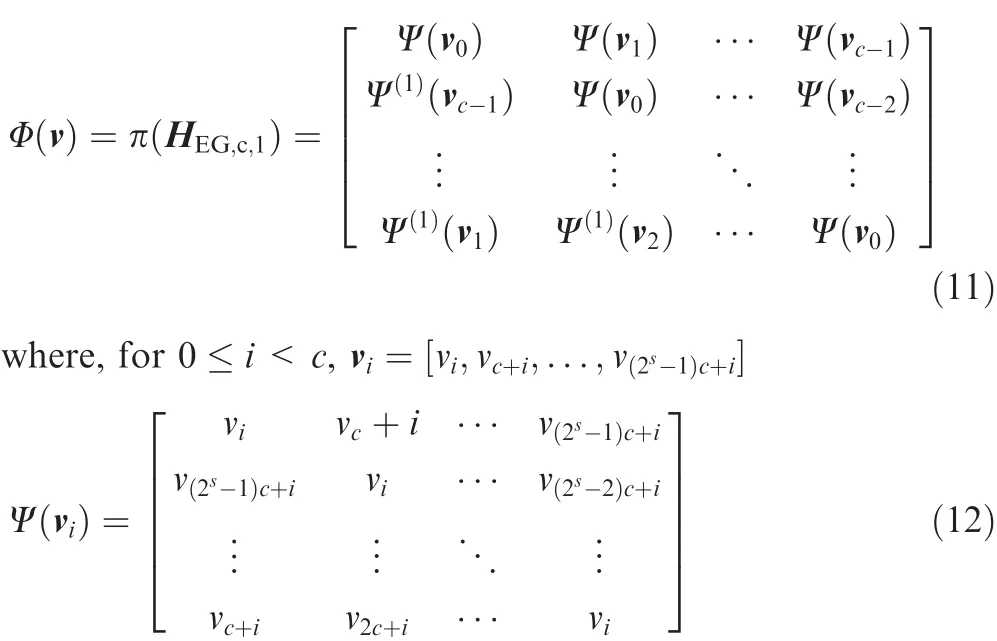
and Ψ(1)(vi)denotes the circulant obtained by simultaneously cyclically shifting all the rows of Ψ(vi)one place to the right.Each 2s× 2scirculant in the array Φ(v)is called a descendant circulant of Ψ(v).

Finally,according to the requirement of code’s parameter,a new HQCcan be formed by selecting some circulants of Φ(v)for masking.Masking operation is to set some circulants to all zero matrices.By masking the base array HQC,HQC,maskis obtained.The null space of HQC,maskdefines the proposed QC-CD-LDPC code.

Example 1.We choose 26as the size of a circulant of QCLDPC code.And we select a properq=127 which is subject toq2-1=(q+1)(q-1)=26×c,wherecis a constant.Then we constructHEG,c,1based on EG*(2,127)and decompose it to π(HEG,c,1)with circulant size of 26.Finally,HQC,maskis constructed by selecting some circulants of π(HEG,c,1)with masking.The null space ofHQC,maskdefines the QC-CDLDPC code.

The QC-CD-LDPC code we proposed here has mainly two advantages in hardware implementation.

Table 1 Hardware analysis of three shifting network implementation methods.

First of all,we design the size of circulant with power of 2.It is supposed to reduce implementation complexity of digital circuit in accumulation and addressing.The most effective hardware overhead economization is on shifting network,which always holds a considerable area in decoder and is influenced by circulant size.There are three common methods for shifting network implementation:Benes network,25QSN network26and Banyan network.27As shown in Table 1,Benes network and QSN network are able to support different circulant sizes in one implementation yet occupy more area.So it will be a waste to use Benes network or QSN network unless in a flexible-code-needed scenario.Banyan network,as the most economical scheme,allows only the input with size of power of 2.Therefore,to maximize the hardware resource usage efficiency,it is a valuable work using algebraic method to construct QC-LDPC code with circulant size of power of 2.

Second,we adopt a design with circulant weight of 1.In the most common way of QC-LDPC decoding,layered decoding,each variable node updates all the edges connected to it within current layer.Thus,it will cause a longer decoding delay of a layer when circulant weight is more than 1.

Compared with other QC-LDPC codes,QC-CD-LDPC codes take almost the same hardware implementation complexity under the same code parameters.Moreover,unlike the existing algebraic QC-LDPC codes,QC-CD-LDPC codes provide flexible code parameters,e.g.,circulant size and circulant weight.As a result,QC-CD-LDPC codes can significantly reduce the complexity of decoder implementation.

If we design nontransparent QC-CD-LDPC codes to resist phase inversion,there may be a slight increase in control circuit.If the average row weight is set to even,the transparent QC-LDPC codes can have all even row weight.However,the nontransparent QC-CD-LDPC codes have to contain at least one row with odd row weight.As a result,the control circuit needs to add a small overhead to control the computing units dealing with rows with different row weights.

A nontransparent(8192,7168)QC-CD-LDPC code is designed by our method based on circulant decomposition with sophisticated masking,whose circulant size is 256,column weight is 4 and row weight is 31.It has higher engineering efficiency than that of NASA,which is presented in Section 5 in detail.

5.Implementation of FEC design

The proposed FEC design can be implemented with better performance and lower resource consumption.For the sake of simplicity,we focus on the above basic channel of AAV to describe and analyze our approach and choose the frame phase inversion probabilityP=0.1.It’s worth mentioning that our approach is also resistant to phase inversion over other frame phase inversion probability and more complex channels,e.g.,Rayleigh channel.

A decoder is proposed for the proposed FEC codes over the basic channel of AAV,i.e.,AWGN with frame phase inversion channel.The proposed FEC codes are nontransparent,which means that a codeword is not a valid codeword after frame phase inversion.If the failure happens after the first traditional decoding,we can believe in high probability that the received symbols are a codeword with phase inversion.Therefore,we can try one more time to decode the phase inversion of the received symbols.The above decoding algorithm that we proposed is called Inversion Resistant Decoding(IRD)algorithm.IRD just uses at most twice traditional decoding without adding extra structures to resolve the phase ambiguous,which simplifies the complexity of implementation.Specifically,if the traditional decoding uses Sum-Product Algorithm(SPA),the corresponding IRD is denoted as IRD-SPA.

A nontransparent(8192,7168)QC-CD-LDPC code is designed by using the methods proposed in Sections 3 and 4,whose circulant size is 256,circulant weight is one and row weight is 31.The performance of this LDPC code is shown in Fig.1.It compares the Bit Error Rate(BER)and Frame Error Rate(FER)of the nontransparent(8192,7168)QCCD-LDPC code(denoted as NT(8192,7168)QC-CD-LDPC in legend)and NASA’s(8176,7156)QC-LDPC code over AWGN channel(denoted as AWGN in legend)and AWGN with frame phase inversion probabilityP=0.1 channel(denoted as AWGN+P=0.1 in legend)decoded by SPA and IRD-SPA.

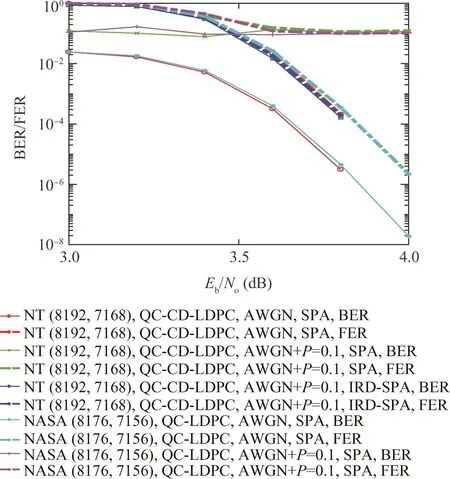
Fig.1 Performance of nontransparent(8192,7168)QC-CDLDPC code.

From the performance curve in Fig.1,we can see that the coding gain of the(8192,7168)QC-CD-LDPC code is better than the(8176,7156)QC-LDPC code adopted by NASA.And the(8192,7168)QC-CD-LDPC code can resist phase inversion with the proposed IRD algorithm,while NASA’s(8176,7156)QC-LDPC code fails in decoding with phase inversion.

Besides performance,our design is more efficient in hardware utilization than that of NASA.The throughput of an LDPC decoder is directly influenced by its circulant size.It is assumed that each iteration needsTidealclocks and its throughput can be delivered as throughput=(n×fmax)/(I×Tideal),in whichnindicates codeword length,fmaxis the highest clock frequency of the hardware andIindicates the average iteration number.Row parallel and block parallel,as two common structures in parallel LDPC decoder implementation,have different calculations onTidealrespectively.In row parallel decoder,Tideal= 「(m×trow)/(C×z),mis parity length,trowis the required clock number of a row,Cis core number andzindicates circulant size.In block parallel decoder,Tideal= 「(n×dv)/(C×z),wheredvis the average degree of each variable node.It can be seen that regardless of parallel mode,the throughput of an LDPC decoder is proportional to the circulant size of the code.Thus the circulant size should be chosen according to the specific demand of decoder throughput.Our construction allows flexible circulant size,which is different from the traditional construction.

According to Table 1,Table 2 gives the estimation of the MUXs usage number under three different shifting network designs for NASA’s(8176,7156)code and the proposed(8192,7168)code.The comparison result indicates that with the design of setting circulant size to power of 2,the hardware consumption of shifting network declines by about 46%by employing Banyan network than Benes network and incidentally drops the whole decoder area by a substantial amount.

Table 3 gives the throughput of NASA’s(8176,7156)code and the proposed(8192,7168)code.It is assumed that the decoder adopts block parallel structure and uses one core,fmax=300 MHz andI=5.It can be seen that the throughput is directly related to circulant size.So the decoder will achieve a lower throughput while using the proposed code than using NASA’s code due to the smaller circulant size.However,the MUXs usage amount per Gbps demonstrates that the decoder complexity of our proposed code is only half of that of the NASA’s code.

From the above analysis,it’s apparent that the advanced FEC design can construct codes with excellent performance and efficiency.Aiming at the demand of reliable communication of a data transmission system,a nontransparent(4096,2048)QC-CD-LDPC code is constructed by the advanced FEC design,whose circulant size is 64,column weight is 3 and row weight consists of 5,6 and 7.We use a transparent(4096,2048)PEG LDPC code,whose circulant size is 64,column weight is 4 and row weight is 8,to compare the ability of resisting phase inversion.The performance of these LDPC codes is shown in Fig.2.It compares the BER and FER of the nontransparent(4096,2048)QC-CD-LDPC code(denoted as NT(4096,2048)QC-CD-LDPC in legend)and the transparent(4096,2048)PEG LDPC code(denoted as T(4096,2048)PEG LDPC in legend)over AWGN channel and AWGN with frame phase inversion probabilityP=0.1 channel decoded by SPA and IRD-SPA.

Fig.2 Performance of nontransparent(4096,2048)QC-CDLDPC code.

Table 2 Estimation of MUXs usage number under three different shifting network designs.

Table 3 Throughput of various LDPC codes.

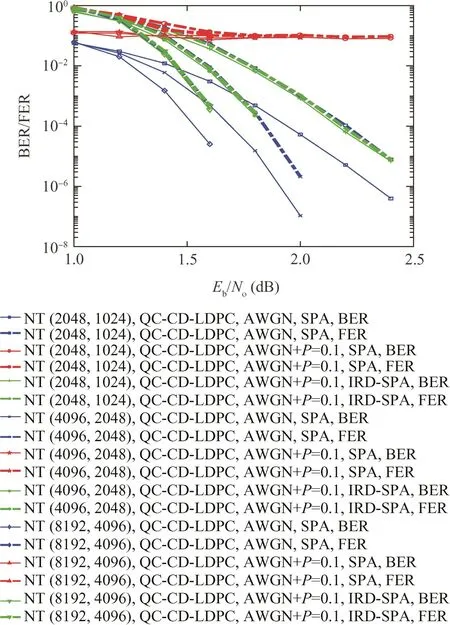
Fig.3 Performance of QC-CD-LDPC codes with same code rate but different code length.

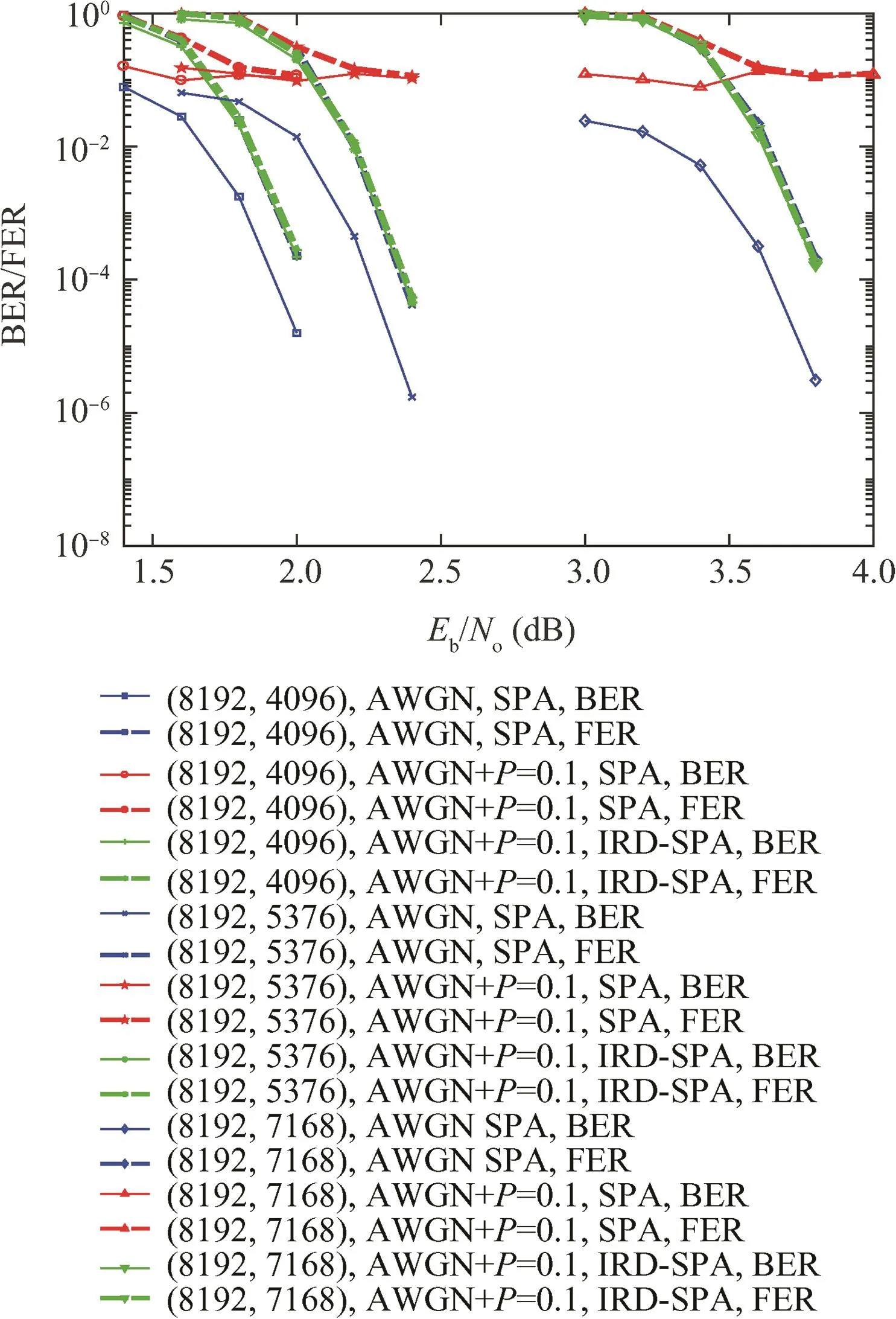
Fig.4 Performance of QC-CD-LDPC codes with same code length but different code rate.

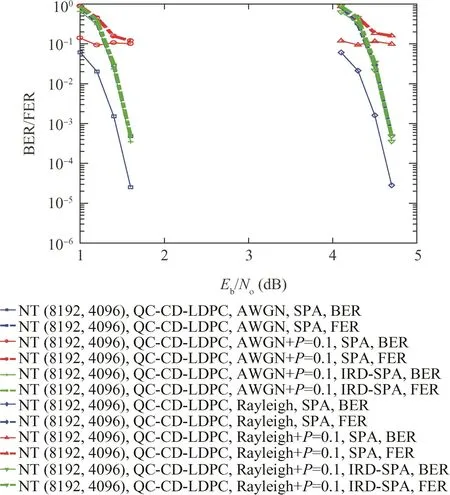
Fig.5 Performance of nontransparent(8192,4096)QC-CDLDPC code over different channels.

From the performance curve in Fig.2,we can see that the nontransparent(4096,2048)QC-CD-LDPC code has ability to resist phase inversion,but the transparent code loses the ability of error correcting with phase inversion.The hardware consumption of this nontransparent(4096,2048)QC-CD-LDPC code,given in Tables 2 and 3,demonstrates the hardware efficiency of our QC-CD-LDPC code.

This code has been adopted in a data transmission system due to its excellent error performance and hardware efficiency.

Furthermore,Fig.3 shows the performance of QC-CDLDPC codes with same code rate but different code length.And Fig.4 shows the performance of QC-CD-LDPC codes with same code length but different code rate.We can see that the proposed QC-CD-LDPC codes with different code parameters keep good error performance and the ability to resist phase inversion.In short,the proposed QC-CD-LDPC codes can suit a variety of different needs of code length and code rate in practice.

Fig.5 shows the performance of the nontransparent(8192,4096)QC-CD-LDPC code over different channels.It compares the BER and FER of the nontransparent(8192,4096)QC-CD-LDPC code(denoted as NT(8192,4096)QC-CDLDPC in legend)respectively over AWGN,AWGN+P=0.1,Rayleigh,Rayleigh+P=0.1 decoded by SPA and IRD-SPA.It shows that the proposed QC-CD-LDPC code keeps good error performance and the ability to resist phase inversion over different channels.

6.Conclusions

In this paper,we have presented an advanced FEC design for remote control and data transmission of AAV.It’s worth mentioning that unlike frame header detection,the proposed method works well for systems,in which one frame header is followed by multiple frames.We verified that nontransparent LDPC codes can solve decoding failures caused by phase inversion.The advanced FEC design based on circulant decomposition keeps nontransparency and realizes the flexibility of code parameters.Experimental results show that the proposed nontransparent QC-LDPC codes have excellent performance and hardware efficiency.

Acknowledgements

This study was supported by Fundamental Research Funds for the Central Universities of China,NSAF of China(No.U1530117),the National Natural Science Foundation of China(No.61471022)and the Young Elite Scientists Sponsorship Program by CAST of China(No.2017QNRC001).