以把握分类标准为教学“支架”

【关键词】分类思想;初中数学;数学思考

【中图分类号】G633.6  【文献标志码】A  【文章编号】1005-6009（2019）91-0071-02

【作者简介】薛瑾，江苏省苏州市教育质量监测中心（江苏苏州，215004）副主任，一级教师。

“数学是思维的体操”，因此，数学教学的一个重要目标，就是要教会学生进行数学地思考。在这里，“教会思考”意味着数学教师不仅仅给学生传授知识，而且更应注重提升学生运用所学知识解决问题的能力，让学生学会思考，形成良好的思维习惯，达成“教是为了不教”这一高层次目标。在初三复习阶段，教会学生有目的、有意识地思考，是培养学生解题能力的关键。

本文以利用分类讨论思想解题为例，以把握分类标准为教学“支架”，浅谈教会学生思考的具体做法。

1.合理分类，通过变式教学让学生学会思考。

把握分类标准，首先要让学生学会在分类标准确定的情况下进行合理分类。同时，通过变式教学，让学生在经历“回顾”与“检验”过程中学会思考。

例1：某等腰三角形的两条边长分别为4cm和6cm，则它的周长为（  ）。

A.10cm B.14cm C.16cm D.14cm或16cm

“分类讨论”思想是指在解决数学问题的过程中，根据问题中所出现的多种情况和可能性，而分别研究的一种常用的数学思想方法。教学中，教师关键是要教会学生如何发现分类依据、确定分类标准、实施不重复不遗漏的分类。在本题中，教师应当引导学生主动回顾等腰三角形相关知识，根据“等腰三角形有三条边，分别为两腰和一底边”，教师可以设问：题目中给出“两条边长分别为4cm和6cm”这一条件，能确定谁是底边长、谁是腰长吗？这一设问旨在让学生自己发现已知条件中的不确定元素，从而发现问题解决过程中的两种可能性：（1）腰长4cm、底边长6cm;（2）腰长6cm、底边长4cm。于是问题便迎刃而解。

为了更好地发挥例题的教学功能，让学生真正地学会思考，解决本题之后，教师可以进一步进行“变式教学”，即把题中的条件改为“两边长为3cm和6cm”，让学生独立去“求此时三角形的周长”。这里看似只改变了一个数据，其实对学生的解题能力要求更高，可以更好地训练和提升学生的思考力。

2.选定标准，通过动态探究让学生学会思考。

把握分类标准，还有一层意思就是在标准多元的情况下需要先行选定标准，不同的标准对应不同的分类方法。

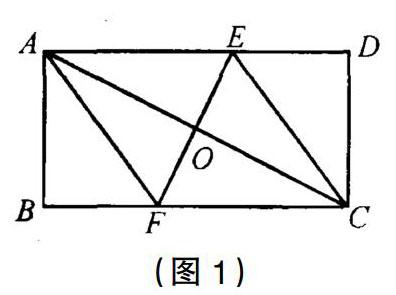
例2：在矩形ABCD中，AB=4cm，BC=8cm，对角線AC的垂直平分线EF分别交边AD、BC于点E、F，垂足为O。

（1）如图1，分别连接AF、CE。求证：四边形AFCE为菱形，并求线段AF的长。

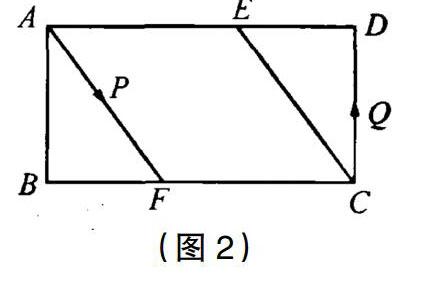
（2）如图2，动点P、Q分别从A、C两点同时出发，沿△AFB和△CDE各边匀速运动一周，即点P自A→F→B→A、点Q自C→D→E→C，一点停则另一点也停止运动。在运动过程中，①若点P的速度为每秒5cm，点Q的速度为每秒4cm，运动时间为t秒，当A、C、P、Q四点为顶点的四边形是平行四边形时，求t的值。②若点P、Q的运动路程分别为a、b（ab≠0），已知A、C、P、Q四点为顶点的四边形是平行四边形，求a与b满足的数量关系式。

在题（2）①的教学中，动点P、Q以不同速度沿着不同路径运动，问题研究起来比较复杂。若将其分成若干种情况逐一研究，就能解决整个问题。为此，教师可以设计不同的“铺垫性问题”，让学生分类探究，使其充分经历和体验思考的过程。

首先，“抓住一点”，实现点上突破。通过对点P运动的分类探究，让学生发现“以点P依次出现在不同路径上的时间范围进行分类研究”的思路。

其次，“两点齐抓”，实现面上突破。研究两个点同时运动的情况，“点P  0秒时在点A处→1秒时在点F处→1.6秒时在点B处→2.4秒时回到点A处，点Q 0秒时在点C处→1秒时在点D处→1.75秒时在点E处→3秒时回到点C处”，指导学生结合双动点同时运动的条件，找到“0

上述引导学生分析的过程，就是引导学生学会如何把握分类标准。在这一过程中，教师要尽可能多地让学生自己去体验、去发现，落实教会学生思考的目标。

题（2）②是对平行四边形存在性问题的研究，不同的判定方法，会产生不同的分类思路。因此，教师可以基于学生提出的判定思路，引导学生通过画图、猜想尝试运用不同的分类标准进行探究。

比如，当学生提出“一组对边平行且相等”的思路时，教师要引导学生有意识地发现“点P、Q必须在互相平行的路径上”的结论，从而得到“当P点在AF上、Q点在CE上”“当P点在BF上、Q点在DE上”“当P点在AB上、Q点在CD上”三种分类情况。又如，当学生提出“对角线互相平分”的思路时，教师要引导学生抓住“线段PQ必经过AC的中点”这一前提，并通过对角线所在直线的旋转得到“对角线交AF和CE”“对角线交边BF和DE”“对角线交AB和CD”三种分类情况，问题便能得到解决。

雅斯贝尔斯在《什么是教育》一书中，多次阐明“自明性”这一观点。他认为，学习任何东西的最好途径是自己去发现、去领悟。这就要求教师在教学过程中，要努力地让学生主动学习，教会他们有目的、有意识地思考，增强“自明性”，才能不断提升问题解决的能力。