矿石颗粒堆积体三维孔隙的CT扫描与量化表征研究

2019-01-14姬程飞

金属矿山 2018年12期

姬程飞

（黄河交通学院，河南焦作454950）

堆浸是指用溶液喷淋矿堆，使液体在往下渗透的过程中选择性地浸出矿石堆中的有用组分，最后从堆底流出的富液中对有用组分进行回收的方法。采用堆浸法回收矿石中金、银、铜等金属是一种经济有效的方法。渗透性是影响矿石堆浸过程有用金属浸出率和回收率最重要的因素［1-4］。矿石颗粒堆积体属松散的多孔介质。与其他任何多孔介质一样，矿石颗粒堆积体的渗透性本质上取决于其孔隙结构特征。孔隙率、孔径分布和孔隙连通度是分析孔隙结构时最重要的3个参数，用以研究孔隙结构和输运系数之间的基本关系［5-7］。用这3个参数来表征矿石颗粒堆积体中的三维孔隙空间结构具有重要意义。然而，由于矿石颗粒的随机分布性，矿石颗粒的形状很不规则，并且试样是松散的，因此其孔隙结构显得非常复杂。在多孔介质孔隙特性的研究中广泛使用的方法有光学显微镜、扫描电子显微镜（SEM）和压汞法（MIP），但均不能用来定量地表征三维孔隙结构［8-10］。作为一种无损检测技术，X射线计算机断层扫描技术（CT）已被广泛应用于许多领域的三维几何形状检测［11-12］。这项技术非常适合于矿石颗粒堆的细观结构观测，其不破坏物料的内部结构，且可以直接获得固相和孔隙相的空间分布特点。此外，由于堆浸形成的矿石颗粒堆积体是一种多孔介质，矿石颗粒和孔隙的密度衰减系数有很大差异，可以满足X射线计算机断层扫描仪（CT）的空间分辨率和密度分辨率的要求。

本研究的主要目的是利用X射线计算机断层扫描和三维图像分析来获取矿石颗粒堆中孔隙结构的关键信息。利用Matlab软件对孔隙率、孔径分布和孔隙连通度进行量化表征，试验结果对深入了解堆浸矿石颗粒堆的渗透特性有重要意义。

1 试验原料及试验方法

1.1 试验原料

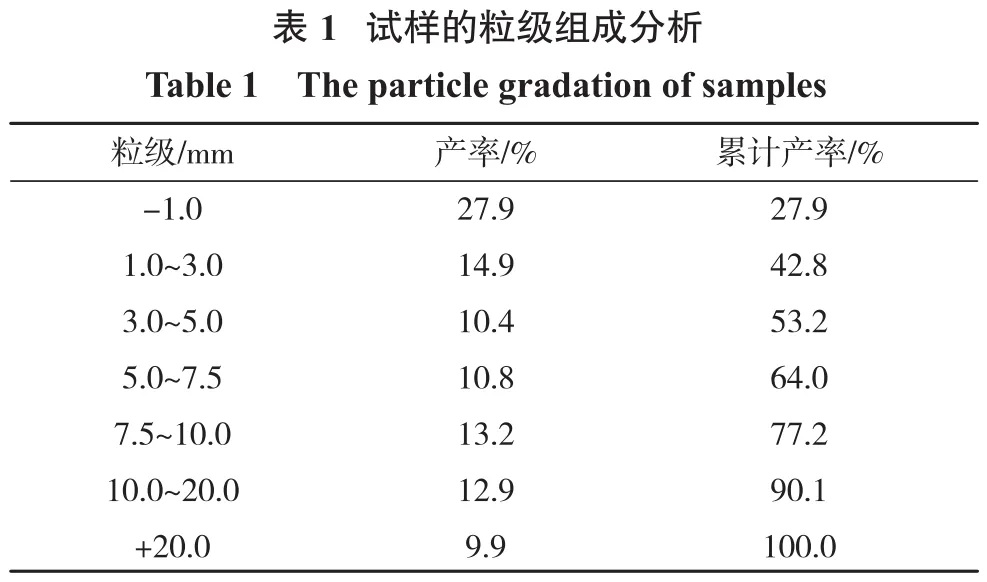
试验用矿样为安徽省铜陵市新桥硫铁矿硫化铜矿石，矿石的粒度分布见表1。可以看出矿石的粒度级配较为均匀。为了研究不同粒度矿石的微观结构。将矿石颗粒进行筛分处理，并将粒径尺寸区间为1～3、3～5、5～7、7～9和9～11 mm的颗粒分别收集，填充在φ50 mm×80 mm的圆柱形有机玻璃柱内。

1.2 CT扫描试验

试验使用SOMATOM医用CT扫描仪，对圆柱形有机玻璃柱内试样分别进行显微CT扫描分析。扫描过程设置CT扫描仪电压和电流参数分别为120 kV和330 mA，扫描的精度约为0.03 mm。经过CT扫描，每个标本可得到大约400张横截面图像。

1.3 图像处理

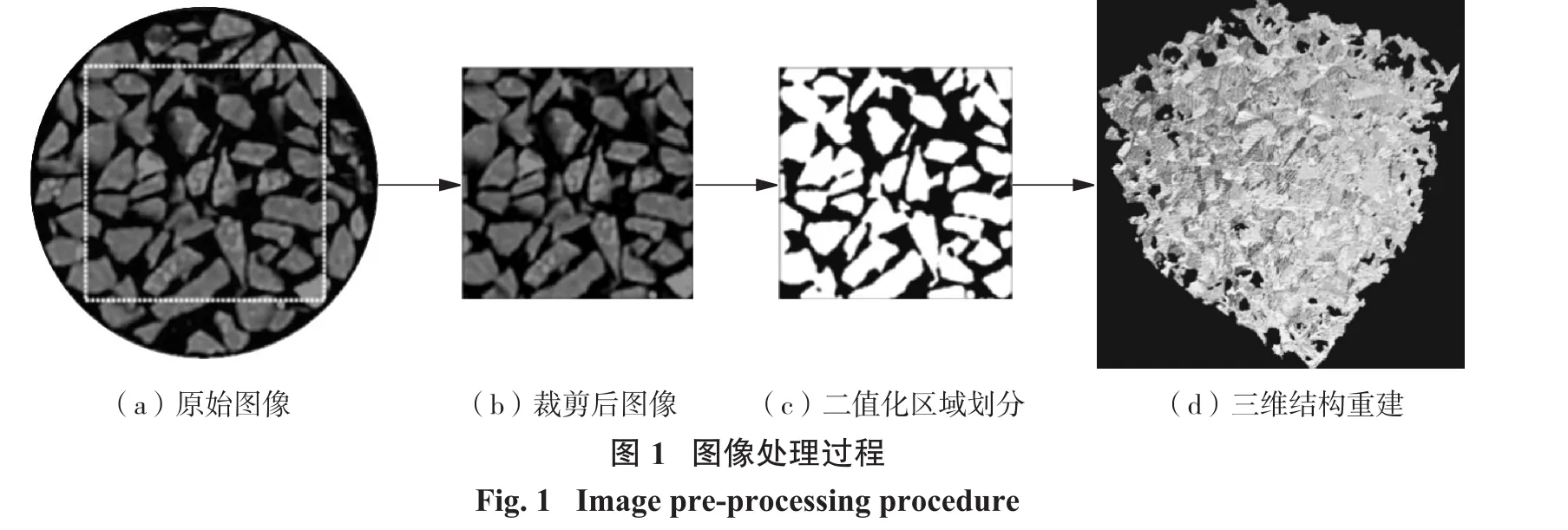
为了保证被测样本内部结构的精确量化，需要对所有的横截面图像进行图像预处理，包括图像的剪裁和分割。本研究采用MATLAB图像处理工具箱编程进行图像处理。首先，将所有原始灰度图像裁剪成360 ppi×360 ppi的正方形图像，然后利用MATLAB软件对图像进行阈值分割，准确分辨每个像素是被固体还是孔隙占据。由于矿石颗粒和孔隙的密度差异很大，因此通过图像灰度直方图的阈值来区分固相和孔隙相是有效的。然而，基于直方图的视觉检查的手动阈值法可能会犯一些错误，使得孔隙相被计为固相，反之亦然。为了克服人工阈值法的局限性，本研究采用自动分割阈值的Otsu方法［13］，该法利用计算机算法自动对灰度值进行统计，并对图像二值化划分区域。在分割完成后，在三维空间中对每组试样的连续二值化图像进行组合。如图1所示，由CT扫描得到的原始图像到三维模型经过了3个步骤，即图像剪裁、图像分割和三维孔隙结构重建。然后利用Matlab软件计算试样的体孔隙率、孔径分布和孔隙连通度。

2 试验结果与讨论

2.1 体孔隙率

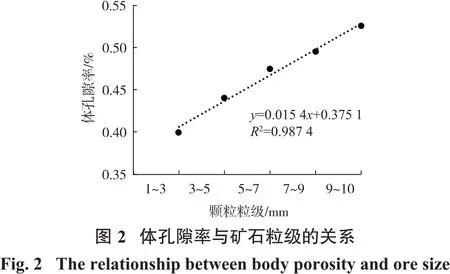
体孔隙率被定义为三维体中的孔隙体素数量与体素总数的比值；面孔隙率被定义为二维截面中的孔隙像素点数量与像素点总数的比值［14］。图2给出了样品的体孔隙率和矿石粒度之间的关系，可以看出体孔隙率随着矿石粒度的增加而增加，且呈明显的线性正相关分布。粗颗粒矿物堆积体的体孔隙率明显比细颗粒矿物堆积体的体孔隙率高。由于大尺寸矿石颗粒具有堆积效应，且颗粒形状不规则度比小颗粒大，造成堆积物的孔隙率随颗粒粒级增加而增大。在颗粒粒度较粗时，单一粒度尺寸区间内被粗颗粒松散地填充，颗粒之间的接触没有细颗粒之间紧密，从而导致体孔隙率随矿石粒度的增加而增加。

图3给出了由三维体统计得到的体孔隙率和由二维截面得到的面孔隙率的对比直方图，可以看出5种试样的面孔隙率与体孔隙率的分布趋势在总体上是相近的。这是因为试样的孔隙面积含量是通过所有二维图像的统计像素数量和总像素数量的平均比值获得的，其原理与三维体孔隙率的获取方法是一致的。经由统计可以得到矿物颗粒堆积体的体孔隙率在0.401%～0.526%之间，面孔隙率在0.383%～0.530%之间，且均随矿石颗粒粒度的增大而增加。

2.2 孔隙尺寸分布

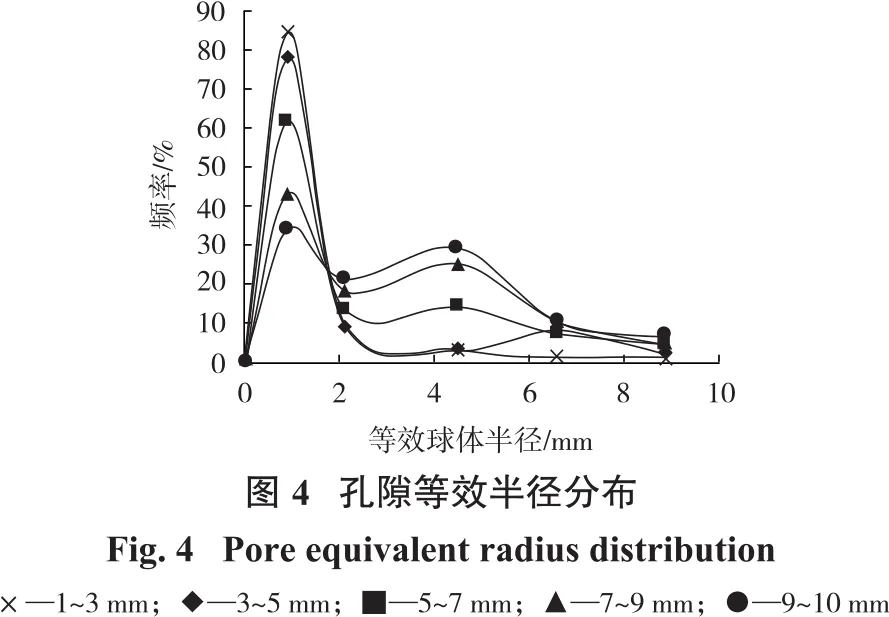
在分析孔隙尺寸分布时，由于孔隙形状很不规则，无法用一个量表征孔隙的尺寸大小，因此采用孔隙等效的方法将所有孔隙等效为球体，利用等效球体半径表征孔隙尺寸。图4表征的是不同粒级的矿石堆积体中孔隙等效球体半径的频率分布情况。从图4可以看出，在小颗粒（1～3和3～5 mm粒级）组成的样品中，孔隙尺寸分布主要以等效半径2 mm以下的小孔隙为主，整体孔径频率的分布曲线向小尺寸孔隙的方向倾斜，如1～3粒级中超过90%的孔隙等效半径小于1.05 mm，只有2%的孔隙等效半径大于2 mm，这种倾斜分布比较符合对数正态分布的特点；其余3种大粒级颗粒组成的样品（粒径5～10 mm）中矿石颗粒较粗且孔隙形状不规则，等效孔径的频率分布范围更宽，可以采用高斯分布对这种分布进行模拟。

中值孔径d50在一定程度上可以反映孔隙的发育程度。图5所示为中值孔径分布曲线。从图5可以看出：随着样品粒度的增加，孔隙的中值孔径明显增大，且在粒径为3～9 mm时，变化速率较大；整体上，中值孔径随颗粒粒级的变化曲线近似于“S”形。

2.3 孔隙连通性

通过簇标记算法，可以检测出样品中某个面与其相对面之间互连的体素的数量。孔隙连通度被定义为被标记的体素与总孔隙体素的比值，这里被标记的体素是顶部和底部表面均相连的孔隙中所有体素的簇［15］。孔隙连通度反映了三维体积中相互连通的孔隙体积占试样总体孔隙体积的比值。

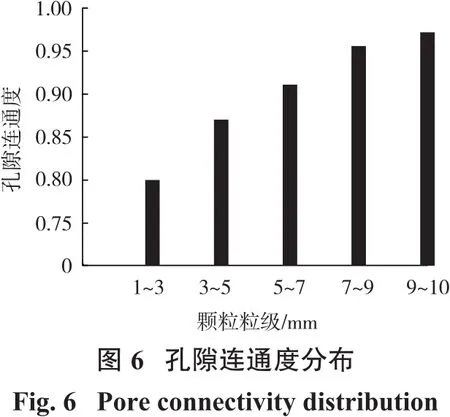
考虑到孔隙结构具有空间变异的特点，从完整的二值化三维模型数据集中提取10个具有200 ppi×200 ppi像素的截面尺寸的随机体，以计算每个样本的平均孔隙连通度。通过将起始坐标移动到2个垂直方向的图像中心以获得各组试样扫描模型的10个随机体。对于每个随机体，用连通的孔体素数除以孔体素的总数来估计其连通度，然后取平均值作为本次样本的连通度，结果见图6。结果表明，5种颗粒粒级样本的孔隙连通性良好，连通度均超过80%，且孔隙连通度随样品粒度的增大而增加，体现了矿石颗粒尺寸的增加对孔隙连通性的贡献。