平面阵分裂波束DOA估计技术研究

匡彪 王琨 袁春姗 要庆生

（昆明船舶设备研究试验中心，昆明，650051）

空间信号到达方向（Direction of Arrival，DOA）估计是阵列信号处理中一个基本的问题。文献[1]表明，分裂波束形成方法具有接近最优的DOA估计精度，并在线阵精确测向中得到广泛应用[2-5]。平面阵相对于线阵，在相同阵元数目的情况下，其尺寸要远远小于线阵，因此在工程上有实际意义。本文以面阵为例，从孔径与信噪比的角度，对分裂波束相关估计与超短基线阵直接相关时延估计定位精度进行性能分析与比较，同时分析分裂阵半波束处理时参考基元选取带来的定位精度影响。

1 方法原理

分裂波束处理是将接收阵列分为具有一定空间距离的不同子阵，对各子阵分别进行波束形成处理，利用不同子阵波束输出估计目标信号到达不同子阵的相位差或时延差信息。现以平面阵为例，平面阵为5×5面阵。阵元编号如图1所示，阵元间距为d，该平面阵按象限划分为4个子阵，每个子阵包含象限内及坐标轴上的9个阵元。

图1 平面阵示意图

选取对称正交的参考阵元各自形成波束，可等效为正交对称四元阵。等效阵型定位示意图见图2(a)。图2(b)为二维波达方向估计示意图，远场声源入射方位角及俯仰角分别为φ与θ，目标相对坐标系xOy的单位方向向量d表示为(sinθcosφ,sinθsinφ,cosθ)。

图2 等效基阵示意图及波达方向估计示意图

传统超短基线四元阵DOA估计原理等同于时延定位原理,如图2(a)所示阵型，建立以等效阵元1～4所在坐标轴的坐标系为x'Oy'，超短基线基阵声学中心位于坐标原点，目标相对坐标系x'Oy'的单位方向向量为d'。假设基线长度为L，c为水中平均声速，Δt为应答测距的双程传播时延，τ14为x'轴的两阵元接收信号时延差，τ23为y'轴的两阵元接收信号时延差，则由平面波近似，可以得到目标S（x',y',z'） 定位方程为：

其中R为目标到超短基线阵的斜距，由下式得到

最终，转换为xOy坐标系，目标位置坐标为

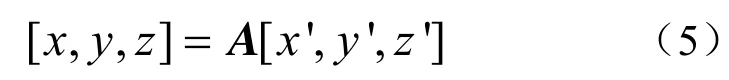
式中A为z坐标轴旋转矩阵。，这里旋转矩阵A表示为

由时延定位方程推出DOA估计方程：

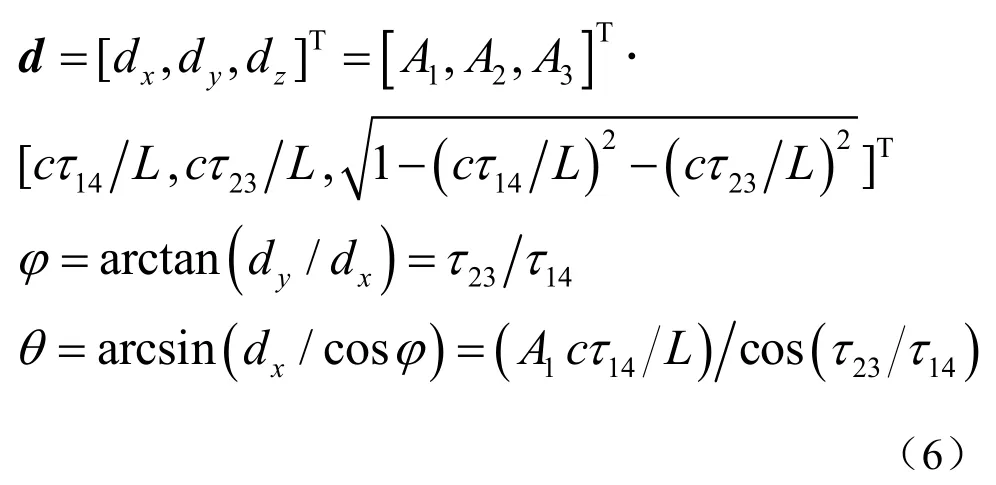
由此，分裂波束方位估计原理如图3所示。xm为面阵中第m阵元接收信号(m=1,2,…,25)，各子阵选取参考阵元进行波束形成，等效为四元平面正交阵，在同一坐标轴的两路等效波束进行互相关，获取相互正交时延数据，利用公式（6）获取方位信息。

图3 分裂波束相关测向原理图

2 分裂波束参考基元选取

如图4所示，参考基元选取主要有两种方式：第一种是以各子阵声中心为参考基元，这种参考基元选取方法主要用于互相关测向；第二种是子阵各阵元均以同一子阵基元为参考点进行相位补偿。两种参考基元选取方法本质上没有不同，仅影响子阵间相位差信息的具体表达，可根据具体应用需求进行选取。

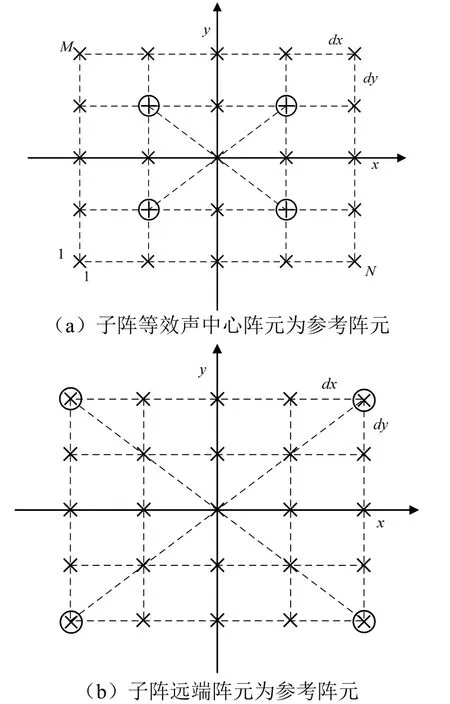
图4 分裂子阵划分及参考阵元选取

假设阵元数为M×N。阵元间距为d，声速为c，入射声波频率为f，当基阵波束对准目标，各阵元接收噪声相互独立，并且信号与噪声也相互独立的情况时，分裂波束相关系统的处理增益为

式中K为各子阵阵元个数，τ为噪声的等效相关半径，T为积分时间。在其他条件相同的条件下，测向精度决定于时延精度与基阵有效孔径，时延估计下限由功率信噪比决定。因此，DOA测向精度应由基阵有效孔径与功率信噪比有关[6]，关系如下式：

式中L为等效基阵孔径，snr为功率信噪比。

选取面阵有效孔径最大的远端4个阵元为正交平面阵模型，采用传统超短基线阵时延估计方法，这里表述为“直接相关法”；以子阵中心阵元为等效点源的分裂波束相关，表述为“分裂波束相关1”；以子阵远端阵元为等效点源的分裂波束相关，这里表述为“分裂波束相关 2”。三种方法孔径及功率信噪比见表1，DOA测向精度随信噪比变化趋势见图5。

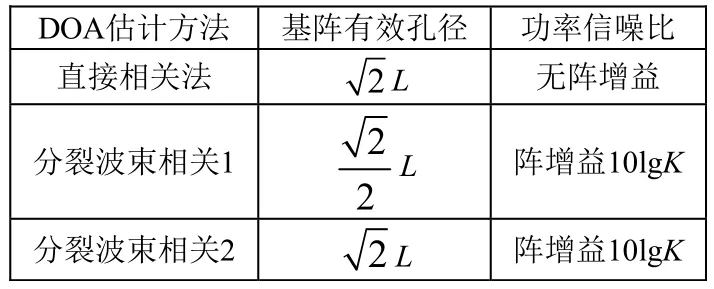
表1 三种方法孔径及功率信噪比对比

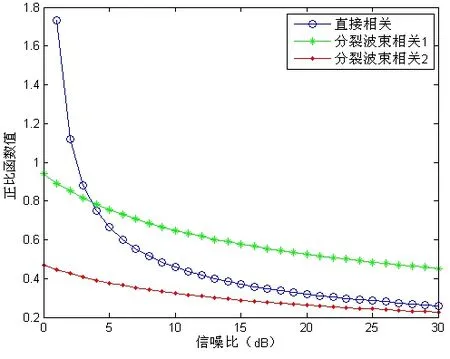
图5 DOA测向精度随信噪比变化趋势

因此可以预见，在检测条件相同的条件下，分裂波束相关2的DOA估计性能应优于分裂波束相关1和直接相关法，在信噪比较低时，直接相关误差急剧增大，在信噪比达到一定值以上，直接相关性能优于分裂波束相关1性能。分裂波束相关法各子阵进行波束形成的过程实际是各路信号相对参考阵元信号延迟滤波并同相叠加的过程。因此从运算量上比较，直接相关法用了两次互相关，分裂波束相关法则需要经过M×N–2次互相关运算，除此之外还需要延迟滤波进行波束形成。相比面阵顶端阵元直接相关，运算量明显增加。

3 仿真分析

仿真参数如下：目标数为1，俯仰角30°，方位角30°，天线阵为5×5的面阵，阵元间距0.05 m，采样率1 MHz，快拍数4 000，两种分裂相关划分的子阵波束形成如图6、图7所示。按上述条件进行50次蒙特卡洛仿真试验，仿真结果如图8所示。结果显示，以子阵远端阵元为等效点源的分裂波束2相关估计性能优于以子阵中心阵元为等效点源的分裂波束1相关估计以及直接相关估计。信噪比较低时，分裂波束相关估计性能远远优于直接相关法，随着信噪比的增高，两者性能接近，在信噪比达到一定值以上，直接相关性能优于分裂波束1相关性能。考虑运算量差异较明显的互相关运算次数，直接相关法经过2次互相关运算，分裂波束相关法经过了23次，运算量增加了十倍以上。

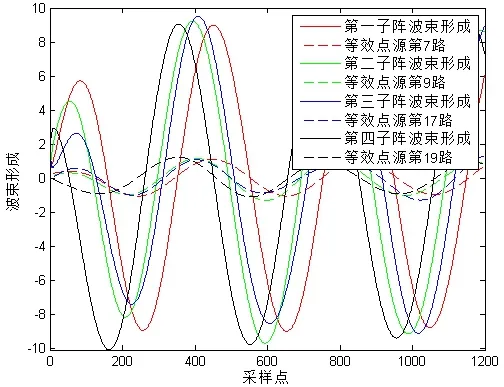
图6 分裂波束相关1波束形成

图7 分裂波束相关2波束形成

图8 分裂波束相关1、分裂波束相关2与直接相关法DOA定位误差比较

4 结论

根据本文的计算及仿真结果可知：（1）结合运算量来考虑，如果目标距离较近，信噪比较高，用直接相关测向较分裂波束法运算量低可满足要求；（2）远距离探测定位，信噪比较低时，分裂波束测向性能较优，并且选取子阵远端阵元为参考阵元的分裂波束模式下，可使增益不变条件下，基阵有效孔径最大，定位性能最好。因此工程实际中可根据测向精度与系统复杂度的需要择优运用。