高浓度气泡群的参数反演

侯森 赵梅 胡长青

（1.中国科学院声学研究所东海研究站,上海,201815；2.中国科学院大学,北京,100049）

在海洋环境中存在着大量的气泡，气泡的来源有自然环境产生的，如风浪形成的气泡和海底甲烷泄漏形成的气泡群等；也有人类活动产生的气泡，如舰船尾流产生的气泡和气幕弹形成的气泡群等。这些气泡不仅会影响海洋环境中的理化性质，而且对声传播也会产生重要的影响，所以获取气泡群的物理参数，对海洋探测和研究水下声信号的传播都有重要的意义。

在对水中气泡群反演方法的研究方面，主要有光学和声学两种方法。光学方法对环境要求较高，不仅需要充足的光照环境，而且需要避免气泡间的影像重叠，在实际应用中适用范围较窄。而声学的方法则对环境要求较低，操作简单且可以对高浓度气泡群进行大面积探测或反演，是探测海洋中气泡群的最主要的方法。

国内对气泡的声学研究主要集中在船舶尾流和海表风成气泡的研究上。通常情况下，这两类气泡浓度较低，空隙率主要集中在 10–7～10–4之间，与此相关的气泡反演方法也主要是针对较低浓度下的气泡参数反演。而在实际情况下，海底甲烷泄漏以及潜艇用气幕弹都可以形成空隙率高达 10–2以上的气泡群。所以研究高浓度气泡群的反演方法在实际应用中有重要意义。早在二十世纪 80年代，钱祖文就对气泡群的反演进行了大量研究，他推导出了考虑气泡间多次散射时的等效入射声场，并解决了实验中阻尼系数远高于理论值的问题[1-3]；到 90年代，Medwin提出了声衰减公式，建立了经典的共振估计模型，并通过大量实验验证了模型可以较精确地反演低浓度的气泡群，但是在反演较高浓度气泡群时存在误差大的问题[4,5]。2011年谢萍将阻尼系数和声速的修正参数引入到经典共振估计模型中，有效解决了频散和声速衰减带来的反演误差，但是反演高浓度气泡群时仍存在误差大的问题[6]。2013年王勇推导了含高浓度气泡水体中的声速模型[7]。

本文对经典的共振估计模型进行了修正和改进，有效降低了对高浓度气泡群的反演误差。通过在经典模型中引入气泡间的相互作用和气泡对声的非共振衰减，较好地解决了理论值明显高于实际值和小半径气泡理论值严重失真的问题。

1 经典的共振估计模型

1.1 共振估计模型理论

经典的共振估计模型认为，声波透射气泡群时的衰减主要是由共振频率与声波入射频率相近的气泡引起，可以通过测量不同频率下的声衰减数据来反演气泡群的半径分布和气泡群浓度等参数。假设声波以频率f入射气泡群时，声波的衰减系数可表示为：

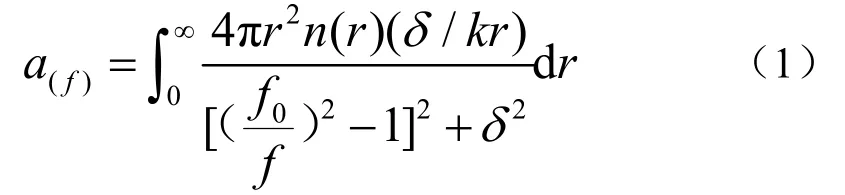
式中，a(f)为声衰减系数，dB·m–1；n(r)为单位体积内半径为r的气泡个数；δ为阻尼系数；f0为气泡的共振频率；f为声波的入射频率。声衰减积分为第一类 Fedholm积分方程，由于其本身不适定的特点，很难直接求解。Medwin基于共振衰减理论对积分做了如下化简并求解出解析式。若入射声频率f近似等于半径为r0的气泡的共振频率，则式（1）可化简为：

式中，f为入射声频率，f0为r0的共振频率，f0与r0的关系式满足：

式中，p0为环境压强；γ为常数 1.4；ρ为密度。式（3）表明在环境参数确定的情况下，气泡共振频率由且仅由气泡半径决定。

将式（3）代入式（2）中求解积分，可以得到不同半径下气泡数量与声衰减的关系：

如式（4）所示，即可以通过测量不同频率下的声衰减得到气泡的半径分布参数。空隙率即单位体积水中的含气量，与气泡群半径分布的关系如下：

式中，β是空隙率，r为气泡半径。在反演得到了气泡半径分布的基础上，可以通过对气泡群半径分布积分来获得空隙率。

1.2 反演气泡群的仿真计算

共振估计模型在气泡群浓度较低时，可以做到较为精确快捷的反演。假设有一气泡群位于浅水环境中，水密度 103kg·m–3，环境压强为105Pa，气泡群为甲烷气体，密度为0.717 kg·m–3，气泡群半径分布满足高斯分布n(r)～N(μ,δ2)，其中数学期望μ为10–4，标准差δ为5×10–5，空隙率为9.72×10–8，气泡的半径分布在 10～250 μm 之间，入射声频率为10～200 kHz.

在低空隙率下，运用经典共振估计法对气泡参数的反演如图1所示。反演得到的半径分布结果与实际分布基本一致，反演得到的空隙率为9.78×10–8与实际值吻合。

图1 经典共振估计法对低浓度气泡群的参数反演

相比于对低浓度气泡群反演时得到的较好结果，经典的共振估计法在反演高浓度的气泡群时会出现非常大的误差。假设一高浓度气泡群所处环境与图1相同且满足同一高斯分布，空隙率为1.38×10–2，运用共振估计模型对气泡群的反演结果如图2所示。

图2 经典共振估计法对高浓度气泡群的参数反演

从图2中可以看出，反演得出的气泡分布明显高于实际的气泡分布，得到的空隙率 2.27×10–2远高于 1.38×10–2的实际值。尤其在小半径气泡的反演上，误差更为明显。这主要有两方面原因，第一点，经典的共振估计模型没有计入气泡间相互作用，在气泡群浓度较高时，气泡间的相互作用会导致气泡群的共振频带展宽，提高气泡群造成的声衰减；第二点原因，论文[3]中实验表明，大半径气泡会对高频率声有较为明显的非共振衰减，随着气泡浓度的增加，这种影响更加明显，所以共振估计法在反演半径范围较广的气泡群时，得到的小半径气泡群数值会高于实际值，即是非共振衰减的影响。

2 共振估计模型的改进

2.1 改进共振估计模型理论推导

为了解决经典共振估计模型在反演高浓度气泡群时误差大的问题，我们建立了改进共振估计模型。一方面我们在模型中引入了气泡间的相互作用，使模型可以适用于对高浓度气泡群的反演。另一方面将非共振衰减引入声衰减计算之中，减小了对小半径区域内气泡群反演的误差。

高浓度气泡群中，气泡之间的平均间距较小，声波在气泡之间会发生多次的散射，文献[2]中给出了等效入射声场的表达式：

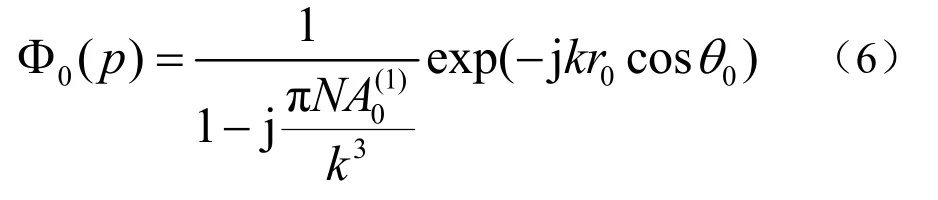
式中，v是气泡瞬时的体积变化，b0是气泡损耗系数，K0是气泡的劲度常数，m0为气泡的伴振质量。对（7）式化简求解可以得到多次散射声场下的气泡等效的劲度常数m和伴振质量K，如式（8）、式（9）所示。

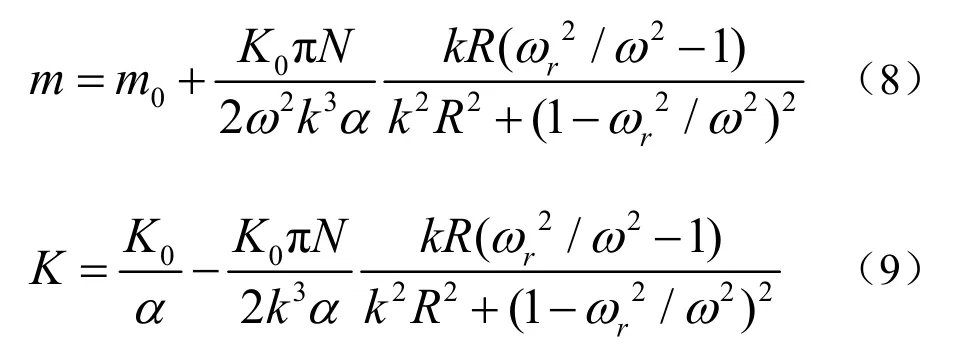
式中，α为多方指数，在过程等效为绝热过程时为1，ωr为不计入相互作用时的气泡共振角频率，ω为入射声的角频率，R为气泡的半径。

进一步通过式（10）可求得在在入射声频率为f时半径为R的气泡的等效共振频率f0。理想情况下，气泡的共振频率仅与气泡半径相关，在考虑了相互作用后，共振频率成为了气泡半径和入射声频率的函数，且具有共振频率展宽的现象：当入射声频率低于气泡共振频率时，共振频率向低频移动；当入射声频率高于共振频率时，向高频移动。

可以通过数值求解积分的方法，反演声衰减系数得到气泡的半径分布和浓度。

2.2 反演高空隙率气泡群的仿真计算

为了验证改进共振估计模型对高浓度气泡群的反演效果，对水中几种较为典型常见的气泡群分布分别做了仿真模拟。气泡的半径为10～250 μm，气泡群的空隙率在 10–2量级，a组气泡群服从高斯分布，期望 100 μm，标准差为5×10–5；b组气泡群服从泊松分布，气泡半径集中在100 μm；c组气泡群服从瑞利分布，气泡半径集中在50 μm；d组气泡群服从指数分布，气泡群主要集中在小半径区。反演结果如图3所示。

图3 反演高空隙率气泡群的仿真

从图3中可以看出，虽然在半径分布的反演上还存在着一些误差，但是相比于经典共振估计法（图2）在反演高浓度气泡群时有了明显的改进。对于不同的分布，得到的结果都比较好，在小半径气泡的反演上没有出现明显的失真现象。

2.3 误差分析

由于气泡空隙率的反演是由对气泡半径分布积分得到，通过空隙率的反演误差可以近似估计整体气泡群分布的反演误差。

对不同浓度下的气泡群的空隙率反演误差做了仿真计算，如图4所示。从图中可以看出，在气泡群浓度较低时，两种模型误差都较小，当气泡浓度较高后经典共振估计模型的误差快速增长严重偏离真实值，改进的共振估计模型误差虽然随气泡群浓度增高有所增加但是一直处于较低水平，在10%以下，反演效果较好。

图4 不同浓度气泡群的空隙率反演误差

3 结论

修正后的共振估计模型与经典估计模型相比，在反演较低浓度的气泡群时，结果相近；在反演高浓度气泡群时，修正后的共振估计模型大大降低了反演误差，将共振估计模型的适用范围从低浓度气泡群扩展到可以对高浓度气泡群的反演。

修正后的模型相比于经典估计模型，增加了计算量，运用共振估计模型反演气泡群时，在浓度较低的情况可以运用经典估计模型；在浓度较高的情况可以运用修正后的模型。本文通过修正扩展了经典模型的适用范围，这将为气泡群的反演研究提供一种新的思路和有益参考。