微器件形状对液桥自组装能力的影响
2019-01-11朱朝飞
朱朝飞, 常 博
(陕西科技大学 机电工程学院, 陕西 西安 710021)
0 引言
微电子机械系统(MEMS)在国民经济与国家安全等相关领域已经证明了其重要意义,作为国家战略必争的前沿高科技因其微型化、成本低和批量化的特点成为全世界增长最快的产业之一[1].伴随着微/纳制造技术的发展,现代微/纳器件的特征尺寸从毫米减小到微米,并向着纳米尺度快速发展,器件的表面效应对MEMS特性的影响也越来越大[2,3].如何实现器件的快速精确装配,成为相关学者的研究重点和难点[4,5].在工程领域利用液体表面张力实现微器件的自组装已经得到了充分的应用.随着MEMS尺度的不断减小,与面积相关的力成为决定系统特性的主要因素.为了更好的借助于回流焊接或者液体表面张力的工艺方法,提高微/纳器件的微组装精度、效率及其成功率,无论是从理论价值或实用价值而言,都有必要充分理解自组装过程中液体表面张力及液桥受力变化的规律[6].
国内外关于液桥受力的研究主要采用以下两种思路:一种是根据平衡液桥内压强具有连续性的原则,从Young-Laplace方程出发,根据液桥表面几何形态建立可解的简化力学模型.但受边界条件或液桥形态的复杂性的限制,该方法仅针对少部分轴对称或悬链曲面进行合理简化后可以直接得到液气界面几何形态的解析解,进而得到其表面张力、毛细作用力等受力情况.另一种是根据能量最小化原理,液体界面形态总是向其系统能量最小值变化至能量最小的稳定形态.该方法通常借助于有限元的思想,可以解决复杂液态曲面的求解问题.
本研究的重点是探究MEMS中常用形状(圆形、方形)微/纳器件与组装基底发生水平错动时,利用液体表面张力实现自组装对齐过程中的液桥受力变化规律.在组装器件与装配基底错动时,液气界面形态表现为复杂的非轴对称曲面,组装圆形或方形结构的微器件时液桥形态特征也不尽相同.因此,本研究将采用有限元的思想建立适当的模型,基于能量最小的原则利用梯度下降法,定量仿真分析不同形状的微器件与组装基底间的液桥在自组装过程中液桥力的变化情况.为提高液桥组装精度、成功率提供理论依据.本研究也可以为微机械电子系统的装配,微通道制造,微流体传输,微器件的黏着失效及相关领域的研究提供理论依据.
1 力学模型及受力分析
1.1 基本组装模型及假设
如图1所示,以圆形和方形微器件的组装作为研究对象.当被组装器件与基底存在水平位置错动Δx时,根据能量最小原则,液体表面张力总是试图通过收缩系统的液气表面积,使系统能量达到最小[7,8],因此必然会产生相应的回复力Fx拖动上部器件向平衡位置运动.
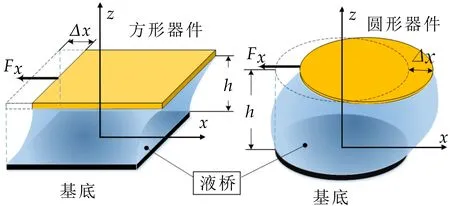
图1 液桥回复力模型
在微器件的自组过程中,为了保证液桥有足够的回复力,液桥的体积必须满足液体布满基底和器件的对应表面.为了研究液桥回复力,首先对液气界面做出以下合理性假设:
(1)自组装过程中,忽略液体蒸发的影响,液桥体积恒定.
(2)液体完全润湿基底的上表面和被组装器件的下表面(液体体积足够大).
(3)自组装过程中液桥高度h不变,微器件平行于基底运动(实际组装过程中高度变化很小).
(4)器件相对基底只在单一方向发生错动且液体不溢出器件或基底.
1.2 能量及回复力计算
在自组装过程中,系统的总能量随着液气表面积的减小向着能量最小的平衡状态变化[6,9,10].系统能量可以表示为:
E=ES+Eg
(1)
式(1)中:ES表示界面能量可通过对面积微元上的表面能积分而来[10]:
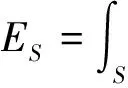
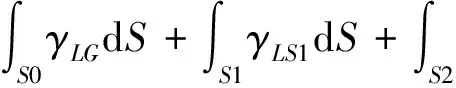
(2)
式(2)中:γLG表示液体和气体界面的表面张力;γLS1表示液体和器件接触面的表面张力;γLS2表示液体和基底接触面的表面张力;S0为液气界面面积;S1为液体在器件上的接触面积;S2为液体在基底上的接触面积.Eg表示液桥系统所具有的势能:
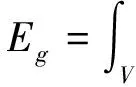
(3)
式(3)中:ρ表示液体的密度;V表示液桥体积;g为重力加速度.根据杨氏方程可知,
γLSi=γSG-γLGcosθi(i=1,2)
(4)
式(4)中:γSG表示气体与固体界面的表面张力;当i=1时,θi表示液体在器件上的润湿角,当i=2时,θi表示液体在基底上的润湿角;将等式(2)、(3)、(4)代入等式(1),忽略积分为0的部分[10]:

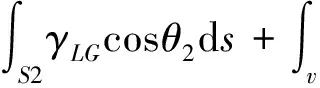
(5)
由于器件自组装过程中,在竖直方面高度不变,即势能Eg的变化对回复力的影响可以忽略,因此器件所受的回复力可表示为[11]:
(6)
2 有限元软件仿真及不同形态液桥回复力分析
2.1 仿真工具及仿真对象参数介绍
自由界面形态的求解问题多是复杂非线性问题,借助于Surface Evolver(SE)软件可以基于最小能量原理和有限元数值分析的方法,通过梯度法实现界面的连续拓扑变换,使所研究的系统能量逼近最小平衡状态,用于分析处理自由表面经过演化形成接近其平衡态的表面形态及系统所具有的能量[12].研究在重力、表面张力以及其他外力作用下一定体积液面形态,迭代计算不同表面积时系统总体能量.基于有限元思想的SE软件将表面离散为由三角微片构成的网络,然后根据能量最小原理智能控制网络演化到最终的平衡构型[13].

表1 仿真器件和液态焊点基本特征参数

图2 器件、基底水平错动下的液气界面形态仿真
2.2 仿真实验及结果分析
以回流焊接工艺过程中的液态焊锡具有的表面张力作为器件的自组装驱动力,分析不同错动量下圆形和正方形微器件周长和面积相同时的液桥受力情况,相关参数如表1所示.液桥系统毛细长度为:

(7)
由表1可知,液桥系统尺寸小于其毛细长度,因此重力相较于表面张力可以忽略不计.
借助SE软件仿真得到如图2所示的仿真结果,其中La、Sa,Lb、Sb,Lc、Sc分别表示正方形器件、圆形器件a和b的周长、面积.由等式(5)可知,在器件相对基底存在不同水平错动量Δd时,液桥系统能量E的变化趋势如图3所示.这符合能量最小原理,即当器件与基底平齐时系统处于受力平衡的稳定状态液桥系统能量最小[14],随着器件与基底错动量的增加,对应的系统能量也不断增大.结合图2和图3分析可知,器件的边长和面积都是影响液桥的系统能量的主要因素.因此要评价方形器件和圆形器件的组装能力,还需要结合器件水平错动时回复力的大小来分析.
根据等式(6)可知,回复力Fx可以由能量对错动量的微分得来.如图4所示的不同错动量下液桥作用在器件上的回复力.回复力Fx的变化趋势与液桥系统能量E的变化趋势是一致的,随着错动量的增加,液桥回复力也不断的增加,但回复力的增加量随着错动的增大而不断减小,并最终会达到一个极限值后开始下降.这是因为当错动量大于一定值时,液体将无法完全覆盖器件或基底的表面,此时随着器件与基底错动量的增加回复力将不断下降.
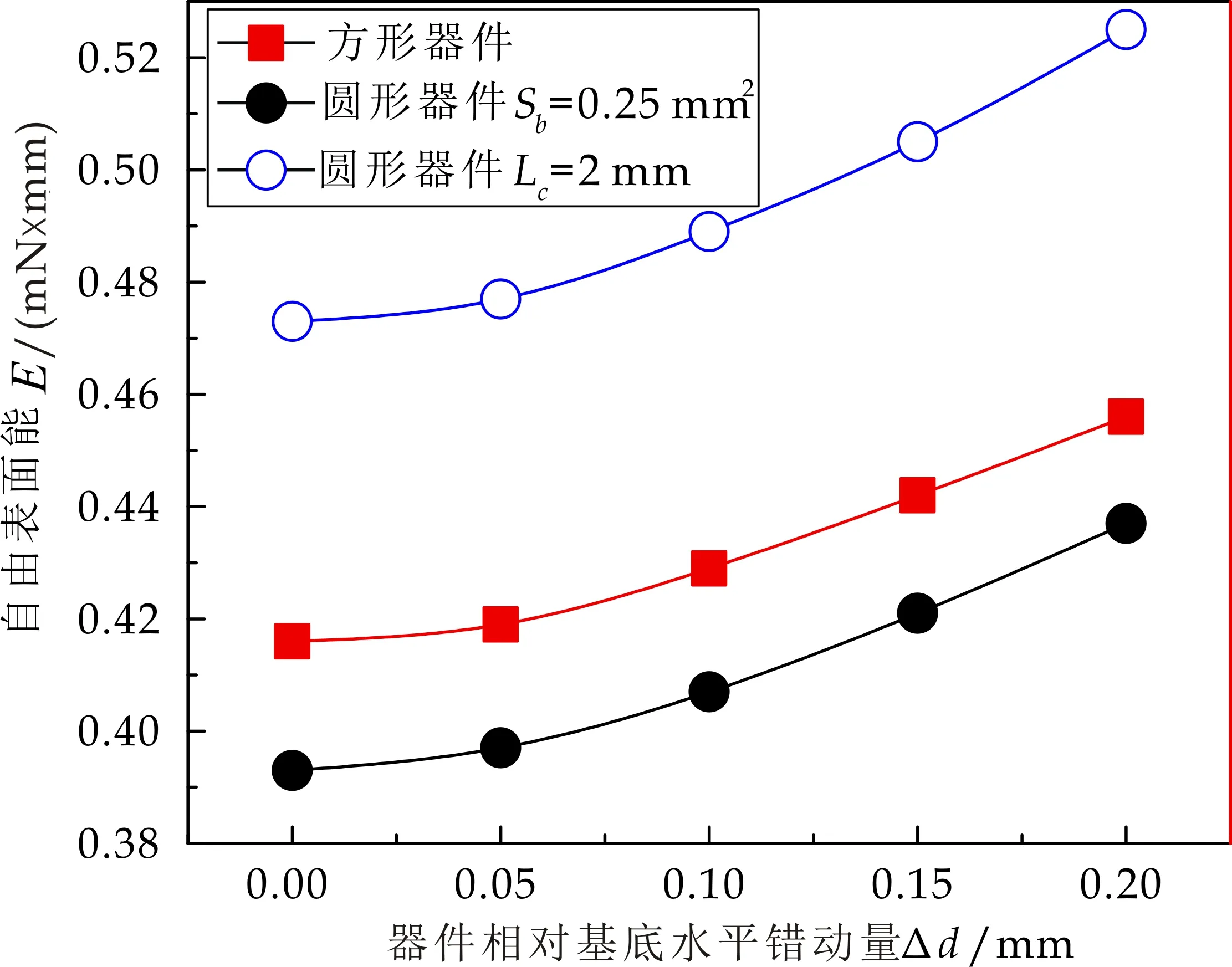
图3 器件在不同错动位置下的液气界面能量变化
结合图2所示的三种尺寸的器件和表1给定的相关液态焊锡参数,分析图4可知:
(1)如图2(a)和图2(b)所示,当圆形器件面积和正方形面积相等时(Sa=Sb=0.25 mm2),正方形器件的周长大于圆形器件的周长(La>Lb).此种情况下,虽然正方形器件间的液桥系统能量大于圆形器件间的液桥系统能量(如图3所示),但反映在回复力上,圆形器件间的液桥回复力大于方形器件间的液桥回复力(如图4所示).
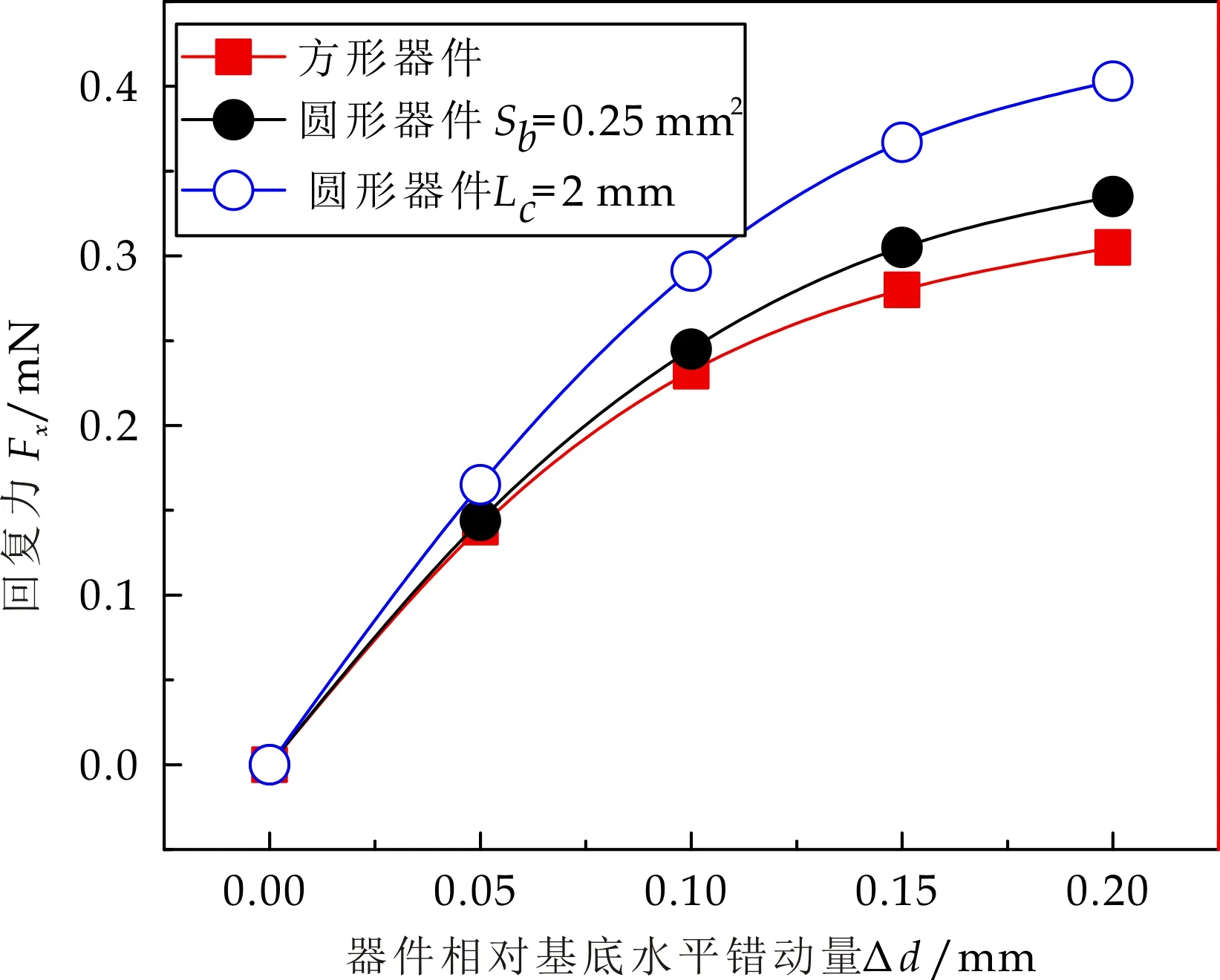
图4 液桥作用在错动器件上的回复力Fx
(2)如图2(a)和图2(c)所示,当圆形器件周长和正方形周长相等时(Sa=Sc=2 mm),正方形器件的面积小于圆形器件的面积(Sa 结合图3和图4,可以明确证明圆形器件可组装能力明显强于方形器件,这也符合工程实践中采用圆形焊盘的电子器件的组装成功率明显高于具有方形焊盘的器件的组装成功率.产生这种现象的本质物理原因是:液桥作用在器件上的回复力主要是因为作用在液气固三相接触线上的表面张力的水平分量产生的.对于圆形器件与基底发生水平错动时,他们之间的液桥表面张力也将在器件或基底的边界约束下沿边界分布,且都能够在水平方向上产生对应的分量.对于方形器件而言,由于平行于错动方向的两边处的液体表面张力未发生较大的角度变化,因此由等式(4)可知其所提供的水平分力很小,水平方向上的回复力主要是由垂直于错动方向上的两个边处约束的液体表面张力提供.因为在相同参数下,圆形器件可组装能力明显强于方形器件,所以在微机械系统中采用圆形器件的组装精度和组装成功率也会高于方形器件. 针对微机械电子工业领域常见的利用液体表面张力组装微小器件的技术,分析器件形状(圆形、正方形)对液体组装能力的影响.本研究采用有限元的思想建立适当的模型,基于能量最小原则利用梯度下降法,定量仿真分析微器件与组装基底间的液桥在自组装过程中系统能量和液桥力的变化情况.从力学的角度证明了在液桥参数相同情况下,圆形器件相比方形器件具有更好的可组装性能.可以为电子装配领域提高液桥组装精度、成功率提供理论依据.本研究结论可以为微机械电子系统的装配,微器件的黏着失效及相关领域的研究提供有益的理论借鉴. 本研究以常见规则形状器件为研究对象,对液桥形态变化进行了适当的简化或假设,忽略了张力自组装过程中的液桥高度变化,具有一定的局限性.另外在实际工业应用中存在形状更加复杂的器件组装问题,还需要根据实际情况具体分析.3 结论
