基于时空上下文与Kalman滤波的视频目标跟踪
2019-01-11李晓静李思禹李长仁
亢 洁, 孙 阳, 李晓静, 李思禹, 李长仁
(陕西科技大学 电气与信息工程学院, 陕西 西安 710021)
0 引言
视频目标跟踪[1]是机器视觉领域的基础问题之一,它是目标识别、行为识别等后续应用的基础,在社会安全、航空航天等重大项目中有着广阔的应用前景[2-5].一般常用的目标跟踪方法包括均值漂移(MeanShift)算法、基于Kalman滤波的目标跟踪、基于粒子滤波的目标跟踪和基于对运动目标建模的跟踪.MeanShift算法[6]可以通过较少的迭代次数快速找到与目标最相似的位置,但是不能解决目标的遮挡问题且不能适应运动目标的形状和大小变化等.对其改进的算法有连续自适应的MeanShift算法(CamShift)[7],此算法可以适应运动目标大小形状的改变,具有较好的跟踪效果,但当背景颜色与目标颜色接近时,容易使目标的区域变大,最终有可能导致目标跟丢.基于Kalman滤波的目标跟踪[8]认为物体的运动模型服从高斯分布来对目标的位置进行预测,然后通过与观察模型对比,根据误差来更新运动目标的状态.基于粒子滤波的目标跟踪[9]每次通过当前的跟踪结果重采样粒子的分布,然后根据粒子的分布对粒子进行扩散,再通过扩散的结果来重新观察目标的状态,最后归一化更新目标的状态.此类算法的特点是跟踪速度快[10],并且能够解决部分遮挡的问题,但是当目标发生严重遮挡时,跟踪效果很差.基于对运动目标建模的方法[11]需要对跟踪的运动目标进行建模,然后利用该模型来跟踪运动目标.此类方法因为要依据先验知识,因此具有一定的局限性.
基于时空上下文的目标跟踪是Zhang等[12]2013年提出的一种目标跟踪算法.该算法基于贝叶斯框架建立了目标与周围内容的时空关系,在低阶特征上对目标与附近区域进行了统计关系建模,通过计算置信图找到似然概率最大的位置即为目标跟踪结果.此算法跟踪速度快,可以实现实时的跟踪,但当目标被严重遮挡时,则容易出现跟错或者跟丢的问题.
综上所述,在运动目标跟踪过程中严重遮挡问题是现有的跟踪算法面临的一项巨大挑战[13],考虑到以上跟踪算法的特性,本文设计了一种基于时空上下文与Kalman滤波的目标跟踪算法,能够解决由于目标被严重遮挡而出现的跟踪失效问题.
1 基于时空上下文的目标跟踪
基于时空上下文的目标跟踪算法的主要思想是通过贝叶斯框架对要跟踪的目标和它的局部上下文区域的时空关系进行建模,得到目标和其周围区域低级特征的统计相关性.然后综合这一时空关系和生物视觉系统上的关注特性来评估新的一帧中目标出现位置的置信图,置信值最大的位置就是新一帧中目标的位置.
在运动目标跟踪过程中,可以将跟踪问题描述为计算一个估计目标位置X似然的置信图:
c(X)=P(X|o)=
∑c(Z)∈XcP(X,c(Z)|o)=
∑c(Z)∈XcP(X|c(Z),o)*P(c(Z)|o)
(1)
式(1)中:X∈R2是运动目标的位置,o表示场景中存在的对象.置信图c(X)中最大的位置X*就是运动目标的位置.从式(1)中可以看到,似然函数可以分解为两个概率部分.一个是建模目标与周围上下文信息空间关系的条件概率P(X|c(Z),o),一个是建模目标局部上下文各个点X的上下文先验概率P(c(X)|o).而目标位置与它的时空上下文关系即条件概率P(X|c(Z),o)需要通过学习得到.
(1)空间上下文模型
空间上下文模型描述的是条件概率函数:
P(X|c(Z),0)=hsc(X-Z)
(2)
式(2)中:hsc(X-Z)表示的是目标和其时空上下文的关系.此模型通过在线学习获得且随着跟踪的进行不断更新.
(2)上下文先验模型
上下文先验模型描述的是先验概率函数:
P(c(Z)|o)=I(Z)*ωσ(Z-X*)
(3)
式(3)中:I(Z)为点Z的灰度值,描述的是上下文Z的外观特征.ωσ是一个加权函数,其定义如下:
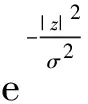
(4)
(3)置信图
置信图的定义如式(5)所示:
(5)
目标X*的位置已知,则可以根据式(5)计算上下文区域中任一点X的似然得出上式中的置信图.其中b是一个标准化常数,α是尺度参数,β是形状参数.
(4)时空模型的学习
基于上下文先验模型和置信图来学习时空模型:
∑Z∈ΩC(X*)hsc(X-Z)*I(Z)*ωσ(Z-X*)=
hsc(X)⊗(I(X)*ω(X-X*))
(6)
式(6)中的卷积可以通过快速傅里叶变换来加速运算:
F(hsc(X))*F(I(X)*ωσ(X-X*))
(7)
由式(7)可以得到学习的空间上下文模型如下:
(8)
根据式(8)可以对时空上下文模型进行更新:
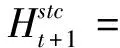
(9)
得到时空上下文模型后就可以在新的一帧图像中计算目标的置信图,置信图中值最大的位置就是目标的位置.
ct+1(X)=
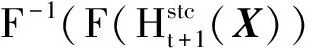
(10)
(11)
基于时空上下文的运动目标跟踪算法步骤如下:
Step1对于第k帧图像,根据第k帧中运动目标的位置学习时空上下文模型;
Step2由时空上下文模型更新公式计算得到第k+1帧的时空上下文模型;
Step3根据第k+1帧的时空上下文模型及上下文先验模型可得到第k+1帧的置信图;
Step4通过计算第k+1帧置信图中的最大值最终得到k+1帧时运动目标所在位置.
2 Kalman滤波
Kalman滤波[14]利用目标的动态信息,设法去掉噪声的影响,得到一个关于目标位置的较好估计.这个估计值可以是对当前目标位置的估计(滤波),也可以是对将来位置的估计(预测),也可以是对过去位置的估计(插值或平滑).本文引入Kalman滤波利用目标的历史位置信息来对目标当前帧的位置进行估计.其中Kalman滤波中的状态变量和观测值均为目标的位置信息.Kalman滤波算法的模型如式(12)、(13)所示:
信号模型:
Xk=AkXk-1+BkXk
(12)
观测模型:
Zk=HkXk+Vk
(13)
式(12)~(13)中:Ak是系统矩阵,Bk是输入矩阵,Xk为状态向量,动态噪声Wk和观测噪声Vk为互不相关的均值白噪声序列;Hk为观测矩阵,Zk为观测向量.
要完成运动目标的跟踪,首先要解决运动目标的模型问题,假设目标是匀速运动的,则运动目标动态特性包括位置、速度,由状态向量Xk=[xk,yk,vxk,vyk]T表示,其中xk,yk分别为目标质心的x,y坐标;vxk,vyk分别为目标速度在x,y轴上的分量;观测向量Zk=[xk,yk]T.
本文所采用的信号模型为:
(14)
观测模型为:
(15)
Kalman滤波方程如下:
时间更新:
(16)
(17)
状态更新:
(18)
(19)
(20)
本文中引入Kalman滤波对目标的位置进行估计,因此输入状态向量uk-1=0.在Kalman滤波过程中观测向量对滤波状态的更新起着至关重要的作用.
基于卡尔曼滤波运动目标跟踪算法的步骤如下:
Step1检测运动目标,并为该目标初始化卡尔曼滤波器,用于预测运动目标的运动状态,并根据运动目标检测的结果,将其作为系统的观测值;
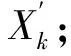
Step3误差协方差矩阵时间更新,由上一时刻的误差协方差Pk-1,得到下一时刻的误差协方差;
Step5误差协方差的修正,根据误差协方差的预测结果修正得到误差协方差矩阵,得到最小化的误差协方差;
Step6运动目标状态的修正,对状态预测结果和观测结果做加权平均,得到当前时刻的状态估计.
3 基于时空上下文与Kalman滤波的目标跟踪
根据基于时空上下文的目标跟踪算法原理可以知道,算法是根据前一帧的时空上下文模型更新计算得到当前帧的时空上下文模型的,而当前帧的时空上下文模型直接决定了当前帧目标跟踪位置的准确性.当目标没有发生严重遮挡时,算法可以准确地跟踪运动目标,但是当目标发生严重遮挡且持续时间较长的情况下,基于时空上下文的跟踪会将遮挡物误认为跟踪目标,从而使得跟踪失效.而Kalman滤波过程包括预测和修正两个部分,其可以根据系统的历史状态信息得到对当前状态的一个较好估计.因而,为了解决跟踪过程中由于遮挡带来的跟踪失效问题,本文考虑当目标发生严重遮挡时,采用Kalman滤波的时间更新,利用目标历史位置信息与运动信息从而得到对当前帧目标位置的一个初始估计.
因此,本文提出了一种基于时空上下文与Kalman滤波的视频目标跟踪算法,其具体过程为:首先通过鼠标手动框出运动目标作为初始化的目标位置,同时对运动目标所在区域进行提取;然后通过基于时空上下文的跟踪算法对运动目标进行跟踪;在每一帧中首先判断目标是否发生了严重遮挡,当目标没有发生遮挡时,则以基于时空上下文的跟踪结果作为Kalman滤波的观测值来更新Kalman的滤波状态;当目标发生严重遮挡时,此时基于时空上下文的跟踪结果失效,则以Kalman的预测值作为Kalman滤波的观测值来更新Kalman的滤波状态.
当目标发生严重遮挡时,基于时空上下文的运动目标检测会出现误跟现象,此时若以其跟踪结果作为Kalman滤波的观测值来更新Kalman滤波的状态必然会导致跟踪错误.因此首先需要判断目标是否发生了严重遮挡.
在通过手动框选运动目标之后,以此时的位置作为目标的初始位置,记为[x0,y0,width,height].在初始帧中提取运动目标所在区域记为img_src,根据当前帧中基于时空上下文的目标跟踪结果[x,y,width,height]提取目标在当前帧中的所在区域记为img_dst,通过计算在不同帧中提取的运动目标所在区域图像对应的灰度直方图向量的相关系数[15]来判断目标是否发生了严重遮挡.
相关系数r是一种数学距离,可以用来衡量两个向量的相似程度.它起源于余弦定理:
cos(A)=(a2+c2-b2)/2bc
(21)
如果两个向量的夹角为0度(对应r=1),说明其完全相似;如果夹角为90度(r=0),则其完全不相似;如果夹角为180度(r=-1),则其完全相反.把余弦定理写成向量的形式:
cos(A)=〈b,c〉(|b|*|c|)
(22)
即:
cos(A)=
(23)
式(23)中:分子为两个向量的内积,分母表示两个向量的模相乘.本文通过设定特定阈值T来判断目标是否发生了严重遮挡,其中0 阈值T的确定:通过统计不同相关系数阈值下遮挡判断的准确率来确定最终的阈值.比如在pets2009视频集的camera2测试视频中,遮挡情况下相关系数阈值分别取0.6、0.7、0.8、0.9时的遮挡情况判断准确率如表1所示. 表1 不同阈值遮挡情况判断结果 由表1的数据可以看到,当阈值取为0.9时遮挡判断准确最好,所以本文将阈值取为0.9.本文仿真实验中其他视频集按照该方法选取的阈值是0.9. 若当前帧中相关系数r小于阈值T时,认为目标发生了严重遮挡,此时将Kalman滤波根据上一帧跟踪结果所得的预测位置作为当前帧Kalman滤波的观测值对当前帧Kalman滤波状态进行更新;若相关系数r大于阈值T时,则认为运动目标没有发生严重遮挡,采用基于时空上下文的当前帧目标跟踪结果作为当前帧Kalman滤波的观测值对当前帧Kalman滤波状态进行更新. 本文提出的改进视频目标跟踪算法流程图如图1所示. 图1 本文提出的改进目标跟踪算法流程图 本文以中科院人体行为分析数据库中的walk视频与pets2009视频集为测试视频,其中walk视频为目标未发生严重遮挡的情况,pets2009为目标发生严重遮挡的情况.在这两组测试视频上分别对MeansShift目标跟踪、基于时空上下文的目标跟踪与本文提出的改进目标跟踪算法进行仿真,其跟踪效果如图2~4所示. (a)未发生严重遮挡情况下的目标跟踪效果图 (b)发生严重遮挡情况下的目标跟踪效果图图2 Meanshift目标跟踪效果图 (a)未发生严重遮挡情况下的目标跟踪效果图 (b)发生严重遮挡情况下的目标跟踪效果图图3 基于时空上下文的目标跟踪效果图 (a)未发生严重遮挡情况下的目标跟踪效果图 (b)发生严重遮挡情况下的目标跟踪效果图图4 基于时空上下文与Kalman滤波算法目标跟踪效果图 通过对比仿真结果图可以看到,当目标未发生严重遮挡情况时,MeanShift目标跟踪当目标颜色与背景颜色接近时出现了误跟,而基于时空上下文的目标跟踪与本文算法的目标跟踪效果较接近,都能实现准确的目标跟踪,且对目标部分遮挡都具有较好的抗干扰性,例如图3(a)里的200帧与图4(a)里的200帧跟踪效果图;当目标发生严重遮挡时,可以看到MeanShift目标跟踪与基于时空上下文的目标跟踪均出现了跟踪失效,如图2(b)里的338帧和380帧跟踪效果图以及图3(b)里的338帧和380帧跟踪效果图.而本文算法依然可以实现准确的目标跟踪,如图4(b)里的338帧和380帧跟踪效果图. 为了定量评价算法的跟踪效果,本文通过跟踪中心误差以及跟踪速率来对算法进行评价.其中跟踪中心位置误差可以用跟踪目标的中心位置(x,y)与手工标注的真实位置(x′,y′)的平均欧式距离来表示.如式(24)所示: (24) 本文以人体行为分析数据库中的walk视频、pets2009中的camera2视频为测试视频,通过手工标定目标的中心位置.其中walk视频中存在背景与前景颜色相近以及部分遮挡等情况;camera2中存在目标被完全遮挡的情况.三种目标跟踪算法在不同视频集上的跟踪中心误差如图5所示. (a)walk视频上的跟踪误差对比 (b)pets2009视频上的跟踪误差对比图5 三种目标跟踪算法在不同视频上的跟踪中心误差变化曲线 通过对比图5中基于时空上下文与本文算法的跟踪中心误差变化曲线可以看到,在目标未发生严重遮挡的情况下,本文算法的整体跟踪误差要小于时空上下文目标跟踪与MeanShift目标跟踪;当目标被严重遮挡时,时空上下文的目标跟踪算法与与MeanShift跟踪均失效,中心误差逐渐增大,本文算法跟踪中心误差虽然也有所增加但是跟踪中心误差最大不超过25,所以综合来看本文算法跟踪中心误差要小于时空上下文的跟踪,算法具有一定的抗遮挡性. 两种算法的平均跟踪速率对比如表2所示. 表2 平均跟踪速率对比 通过表2可以看到,本文算法由于加入了Kalman滤波机制,因此平均跟踪速率相较于时空上下文跟踪有所提升,可以达到20帧/s,因此可以实现目标的实时跟踪. 针对目标跟踪过程中,当目标发生严重遮挡时基于时空上下文的目标跟踪算法容易出现跟踪失效的问题,本文提出了一种基于时空上下文与Kalman滤波的视频目标跟踪算法,能够克服当目标发生严重遮挡时误跟与错跟的问题,可以实现准确的目标跟踪,且能够实时跟踪运动目标.但是在跟踪过程中算法并没有考虑多尺度目标跟踪的问题,因此在后续工作中将加入多尺度因素从而使算法能够达到更好的跟踪效果.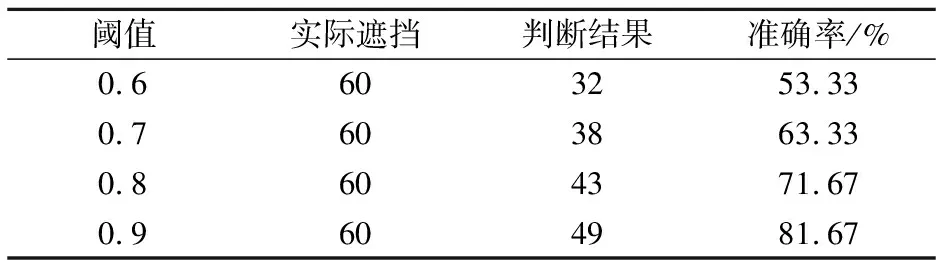

4 仿真结果分析















5 结论
