流场中轻浮颗粒下拉方式数值模拟与对比分析

刘渝丰，陈 炯，李 蒙，孙江龙,3,4，解 德,3,4，刘 曾,3,4

(1.华中科技大学船舶与海洋工程学院,湖北 武汉 430074；2.九江职业技术学院船舶与海洋工程技术研究所,江西 九江 332000；3.高新船舶与深海开发装备协同创新中心,上海 200240；4.华中科技大学船舶与海洋水动力湖北省重点实验室,湖北 武汉 430074)

在以反应物质充分混合为加工前提的化工、医药、冶金、食品等领域中，混合搅拌过程是其生产阶段能耗较大的环节，以国内冶金企业为例，其湿法冶炼车间50%以上的能量消耗几乎都源自搅拌作业环节，如何降低能耗并获得良好的搅拌混合效果是相关产业界亟待解决的实际问题，因此针对搅拌槽内颗粒在混合过程中的行为特点开展研究就显得十分必要[1]。轻浮颗粒因自身密度往往低于液体密度，故趋向于在液体表面层层聚集，也因此造成颗粒与液体不能完全接触。此外，轻浮颗粒相比重颗粒在搅拌过程中更易受到表面涡、表面张力和浮力等的联合作用，导致其在搅拌过程中的行为表现更加复杂[2]。传统的轻浮颗粒搅拌主要依靠叶轮旋转来下拉颗粒至液体中并使其分散[3]，而已有的研究结果表明，使用上下振动的圆盘振动混合器进行轻浮颗粒搅拌操作时，颗粒下拉分散效果会更好，且生产效率更高,如Brauer[4]的研究证实，相比传统叶轮式搅拌器，圆盘振动混合器搅拌系统均质化所需的时间更短。Brauce等[5]在生物学实验中发现，叶轮搅拌器中由叶轮快速转动所产生的剪切力会破坏细胞体，而圆盘振动混合器则能避免这一现象。圆盘振动混合器中由往复圆盘产生的流场比传统搅拌器中的流场状况更加复杂[6]，Wójtowicz[7]对比分析了轻浮颗粒在叶轮搅拌器和圆盘振动混合器中的下拉分散效果，与叶轮搅拌过程中形成的环状流场不同，圆盘振动混合器中上下往复运动的圆盘不断驱动液体，导致其产生较强的轴向流动，在适当的圆盘直径和离底间隙条件下，振动混合器中颗粒分散所耗功率相比叶轮搅拌器相应值可降低11%～30%。有鉴于此，本文基于Fluent软件，采用VOF(流体体积)模型和DPM(离散相模型)对轻浮颗粒在振动混合器和叶轮搅拌器中的下拉过程进行数值模拟，分析了轻浮颗粒下拉的原理，重点探讨了不同参数对振动混合器搅拌效果的影响，并与传统叶轮搅拌器的搅拌效果进行对比，以期为实际生产混合搅拌作业时搅拌器的正确选取提供参考。

1 模型的建立

1.1 VOF模型

Khazam等[8]认为液相涡对颗粒的分散有很大的影响，故本文采用VOF模型模拟表面涡。搅拌槽内流场模拟的基本方程为：

连续性方程

(1)

多相流的连续方程

(2)

体积分数方程

(3)

动量方程

(4)

式(1)～式(4)中：α表示颗粒相体积分数；ρ为流体密度；t为流体运动时间；υ为流体速度矢量,υ1、υ2表示不同方向的速度矢量；ui(i=1,2,3)为沿i方向的流体速度矢量分量；V为物体体积；S为物体的外表面积；n为物体外表面的单位法向量；c为流体的体积分数；τs为应力张量；f为体积力矢量。

1.2 DPM模型

将流体的表面张力系数设置为0.072 n/m，DPM模型的控制方程为

(5)

式中：u为流场速度矢量；up为颗粒速度矢量；τr为颗粒表面的受力分量；gx为重力加速度分量；ρp为颗粒密度；F为作用在颗粒上的外力。

1.3 搅拌器模型

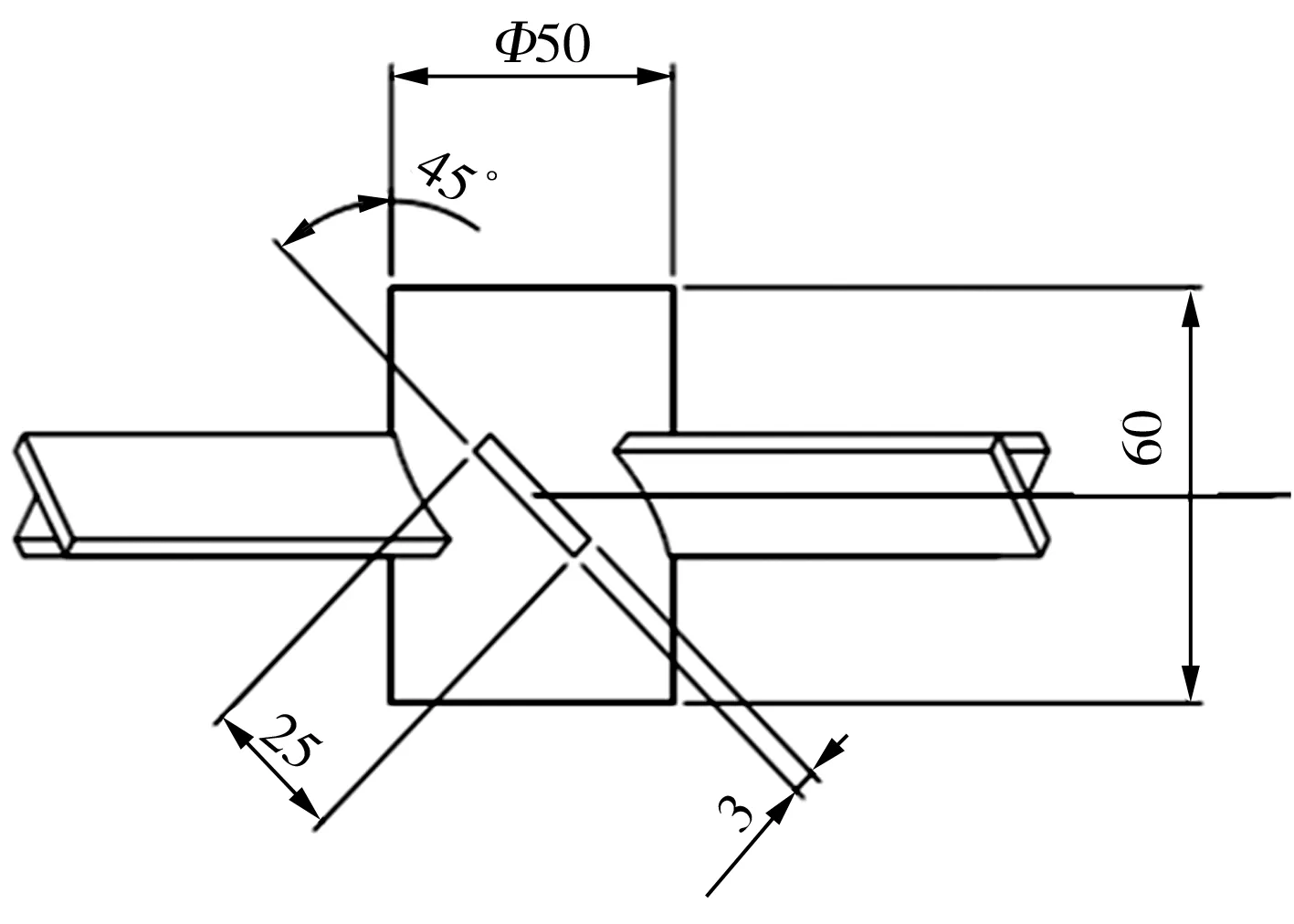
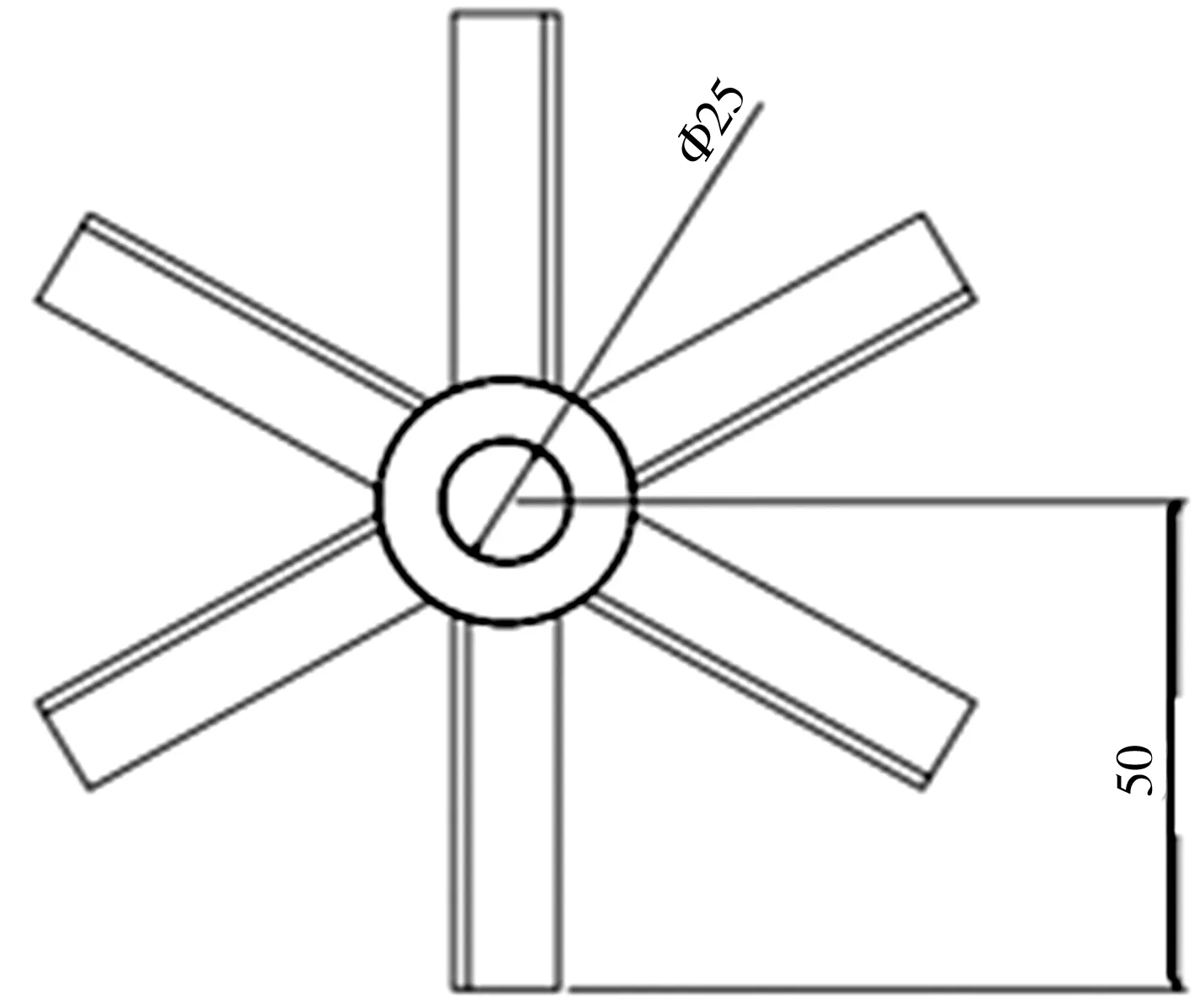
本文选取叶轮式搅拌器和圆盘式振动混合器作为研究对象。其中叶轮式搅拌器参考Wójtowicz[7]的实验结果，选取搅拌效率最佳的斜叶桨式搅拌器，其模型如图1所示。图1(a)中圆柱形搅拌器罐底面直径为0.29 m，罐高为0.4 m，静液面高度H为0.29 m，此外，在装备叶轮的搅拌罐中单独配置宽度B为0.01 m的四个平面挡板。搅拌器中叶轮直径dt为0.05 m，叶轮厚度gt为0.06 m，叶片长度D为0.05 m，叶片厚度a为0.003 m，叶片宽度b为0.025 m(见图1(b)、图1(c))。设定叶轮与罐底的距离(离底间隙)hy分别为0.0725、0.0957、0.1450、0.1943、0.2175 m，叶轮旋转速度为300 r/min。

圆盘式振动混合器模型如图2所示。圆柱形振动混合器罐底面直径为0.29 m，罐高为0.4 m，静液面高度H为0.29 m，其中实心圆盘直径Dc分别设定为0.204、0.220、0.238、0.260、0.276 m，圆盘厚度gd为0.003 m。圆盘与罐底的距离(离底间隙)hp取值与hy相同，混合器工作时的振动频率f为4.17 Hz，振动振幅A分别为0.02、0.03、0.04、0.05 m。

(a)搅拌器主视图

(b)叶轮片正视图

(c)叶轮片俯视图

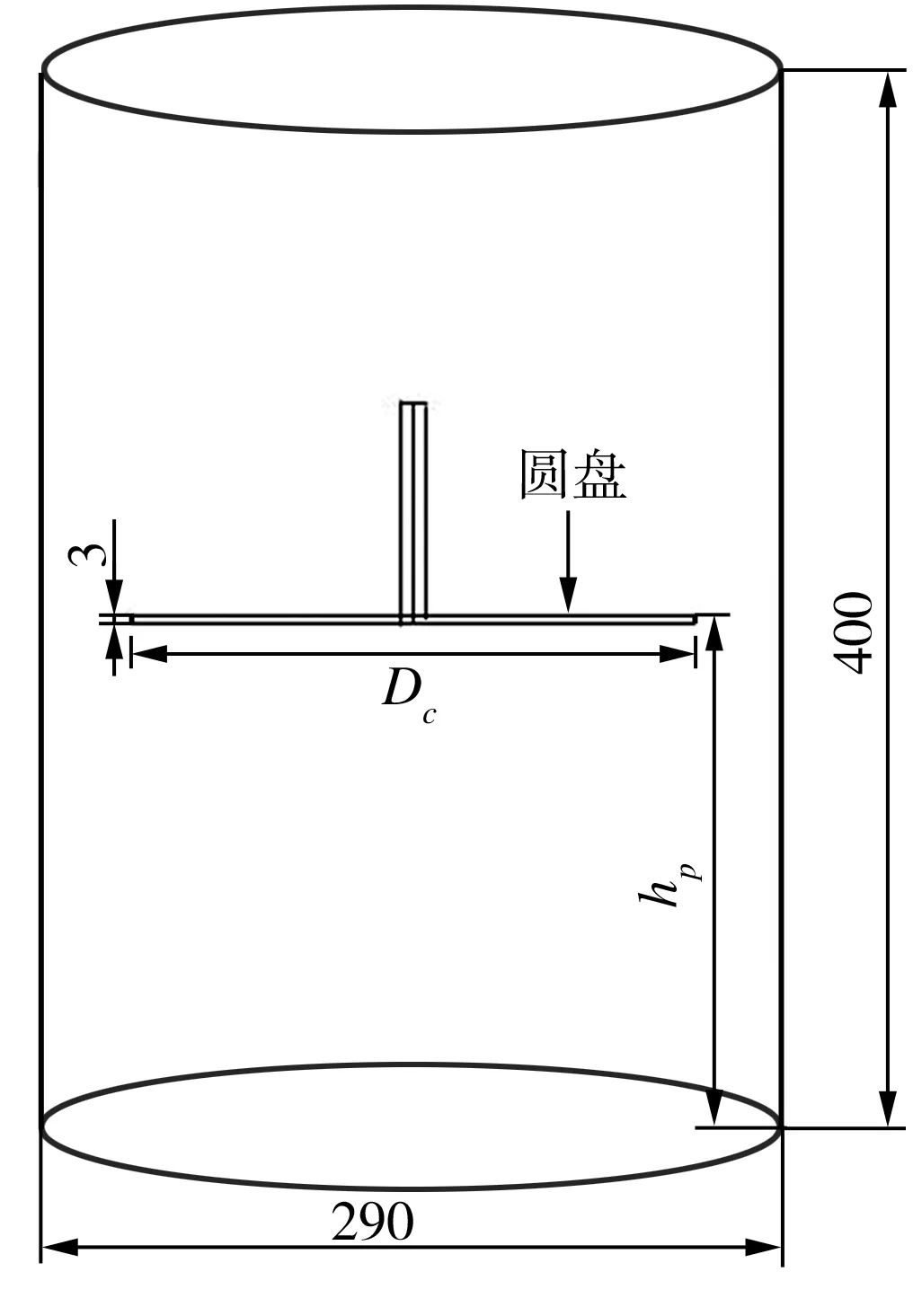
图2 振动混合器模型Fig.2 Model of vibratory mixer

在两种模型中均选取水为搅拌液，其密度为998 kg/m3，运动黏度为0.894×10-3Pa·s；使用粒状聚乙烯作为轻浮颗粒，其密度为920 kg/m3，颗粒直径为0.5 mm。在搅拌开始之前，将1000个轻浮颗粒均匀分布在水面上。

1.4 网格模型和设置

多重参考系和滑动网格法均可用来模拟不同域间网格的相对运动，Tamburini等[9]的研究表明，滑动网格法模拟效果更佳，故本文采用该法进行数值模拟。基于Sun等[10]的网格敏感性研究，综合考虑不同网格数量条件下的计算量及计算精度，将叶轮搅拌器和振动混合器模型中的网格数分别设定为95万和74万。此外，在振动混合器模型中建立不同域间的网格结合交界面，边界条件设置为interior条件，同时利用udf文件控制圆盘的运动。

1.5 计算方法

将整个流场域沿轴向等体积划分为10层以计算颗粒分散度。离散颗粒在搅拌罐中分散程度的计算公式为[11]

(6)

式中：σ为颗粒的分散度，nl是整个计算域的分层数，xj是第j层粒子数，Vj是第j层的体积，X、V分别为颗粒和液体的总体积。理论上当分层的数量足够多时，初始分散度等于1。在搅拌过程中，颗粒逐渐被下拉分散，分散度值越小表明颗粒分散程度越好，分散度接近于0时表明颗粒已完全分散。

圆盘振动混合器消耗功率P的计算公式为

(7)

其中T表示圆盘运动周期，w为圆盘上下运动时的瞬时速度。叶轮式搅拌器消耗功率P的计算公式为

P=2πNM/60

(8)

其中N为叶轮旋转速度，M为叶轮扭矩。

在搅拌开始前，所有颗粒均匀分布在静止的液面上，初始分散度为1。

2 结果分析

2.1 叶轮搅拌器模拟

叶轮搅拌器中颗粒在不同时刻的分散状况如图3所示，由图3可见，当叶轮开始转动后，搅拌器中形成表面涡速度较高的环形流场将颗粒从液面处下拉，大多数颗粒集中分布在叶轮下方一定的高度层，随着搅拌的进行，1 s后颗粒明显分散(见图3(a)和图3(b))，2 s以后颗粒分散程度基本稳定(见图3(c)～图3(e))。叶轮与罐底不同距离条件下搅拌器中的颗粒分散度及搅拌消耗功率变化曲线如图4所示，由图4可见，在叶轮搅拌器中，叶轮与罐底之间的距离对颗粒分散有较大影响。当叶轮与罐底间距较小时，液体射流加强了罐内流场的径向循环(见图5)，将颗粒更快地从表面拉入液体中，但当叶轮向上接近液面时，颗粒分散效果明显变差，这是因为中心涡流对颗粒的下拉深度有限。

(a)0.8 s (b)1.4 s (c)2.7 s

(d)3.4 s (e)4.8 s

图3叶轮搅拌器中颗粒的分散过程

Fig.3Dispersionofparticlesintheimpelleragitator

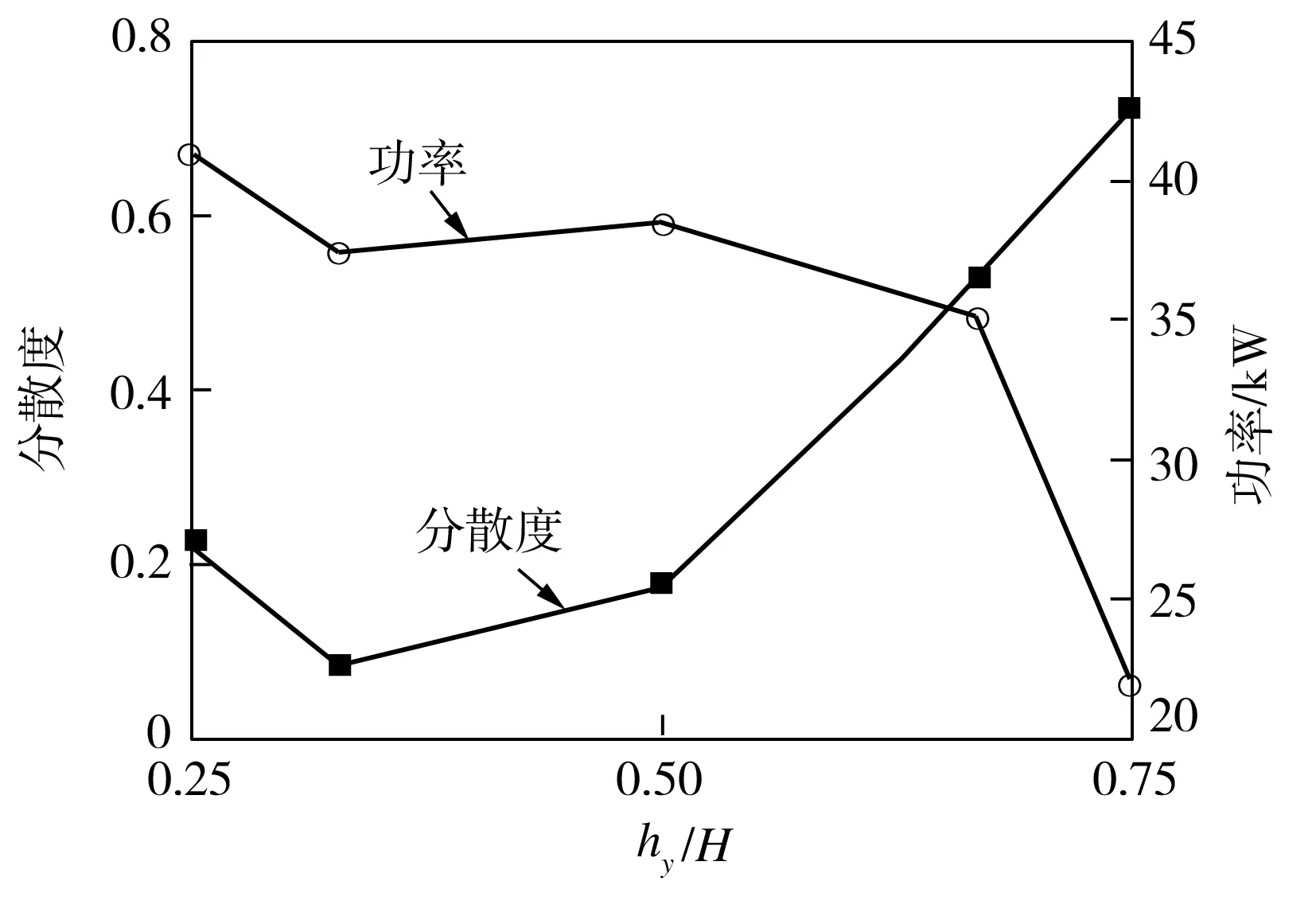
图4 叶轮搅拌器中的颗粒分散度及功率消耗

Fig.4Particledispersionandpowerconsumptionintheimpelleragitator

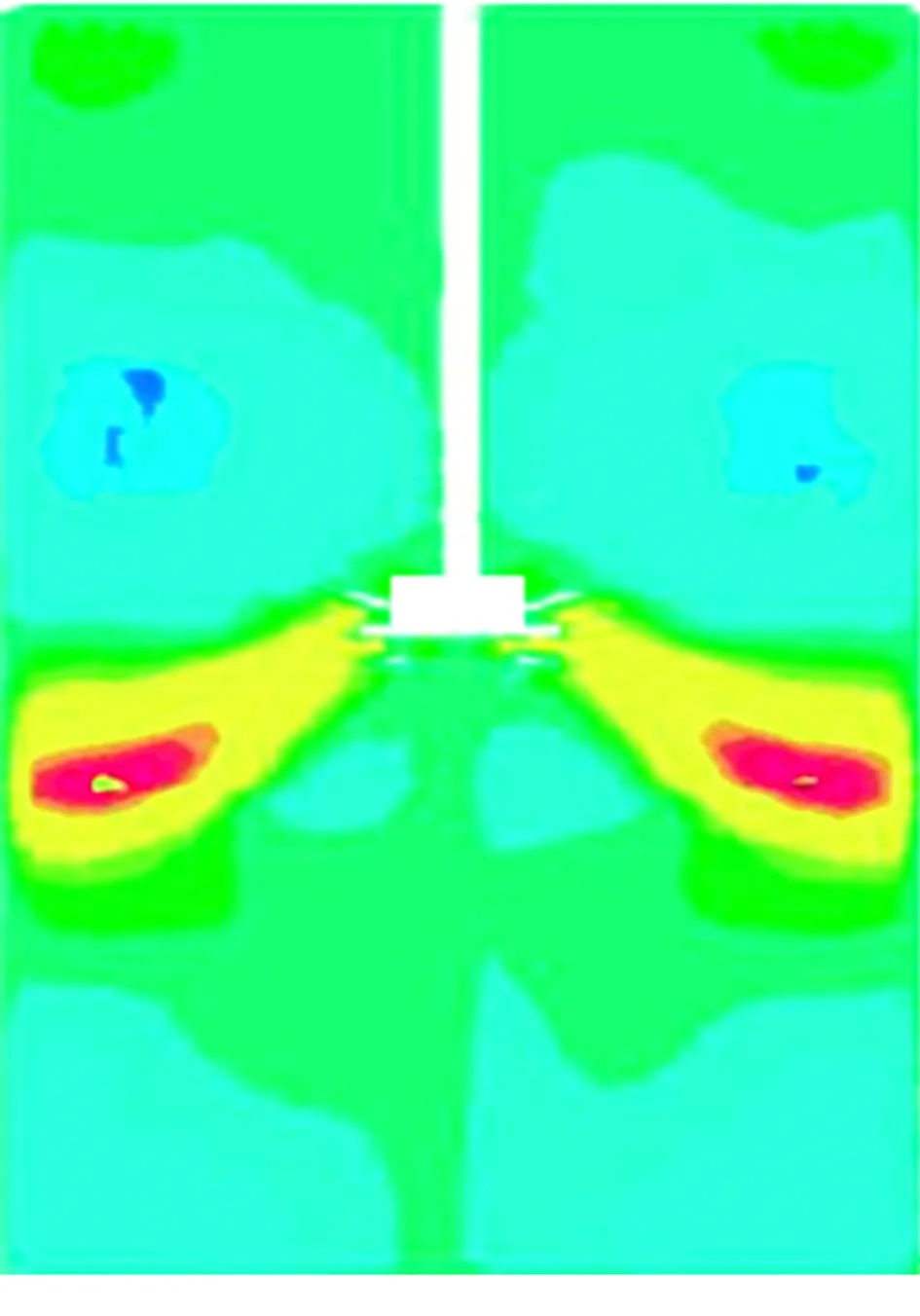
图5 叶轮搅拌器中的流场径向速度Fig.5 Radial velocity of flow field in the impeller agitator

2.2 振动混合器模拟

振动混合器中颗粒在不同时刻的分散状况如图6所示，由图6可见，当圆盘开始振动后，随着液面的波动，1 s后颗粒明显分散，颗粒随着液体流动集中在液面中心处，随后颗粒在圆盘往复运动中下拉，分散效果显著提高(见图6(a)～图6(c))，6 s以后颗粒分散程度基本稳定(见图6(d)和图6(e))。振动混合器中流场主要流动模式为轴向流动(如图7所示)，表现为大规模的轴向对称环形旋涡以及圆盘和罐壁之间的强烈对流。圆盘引起的强轴向流动与叶轮搅拌器中的环形流动不同，颗粒在振动混合器罐体空间中所有位置处都能被强力向下吸入液体中，因此由圆盘振动产生的轴向-径向流动对轻浮颗粒下拉和分散的效果更好。

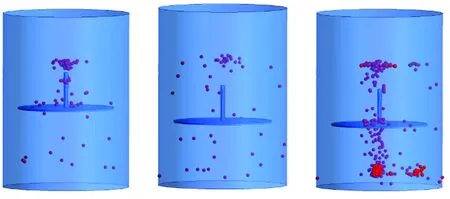
(a)1.2 s (b)3.4 s (c)6.8 s

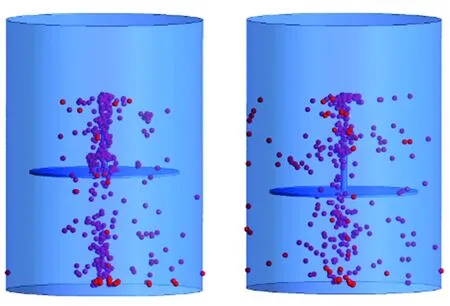
(d)9.2 s (e)12.7 s

图6振动混合器中颗粒的分散过程

Fig.6Dispersionofparticlesinthevibratorymixer

图7 振动混合器中的流场轴向速度Fig.7 Axial velocity of flow field in the vibratory mixer

当圆盘直径为0.204 m，振动振幅为0.03 m时，圆盘与罐底不同距离条件下振动混合器中的颗粒分散度及搅拌消耗功率变化曲线如图8所示。从图8中可以看出，随着圆盘与罐底距离的增大，颗粒的分散度呈现出先减小后增加的趋势，分散效果变化明显，与此同时，混合搅拌的功率消耗却在不断增加。因此，在振动混合器中，圆盘与罐底的距离偏大或偏小都将导致分散度变差，圆盘处于居中位置将获得较好的分散效果。

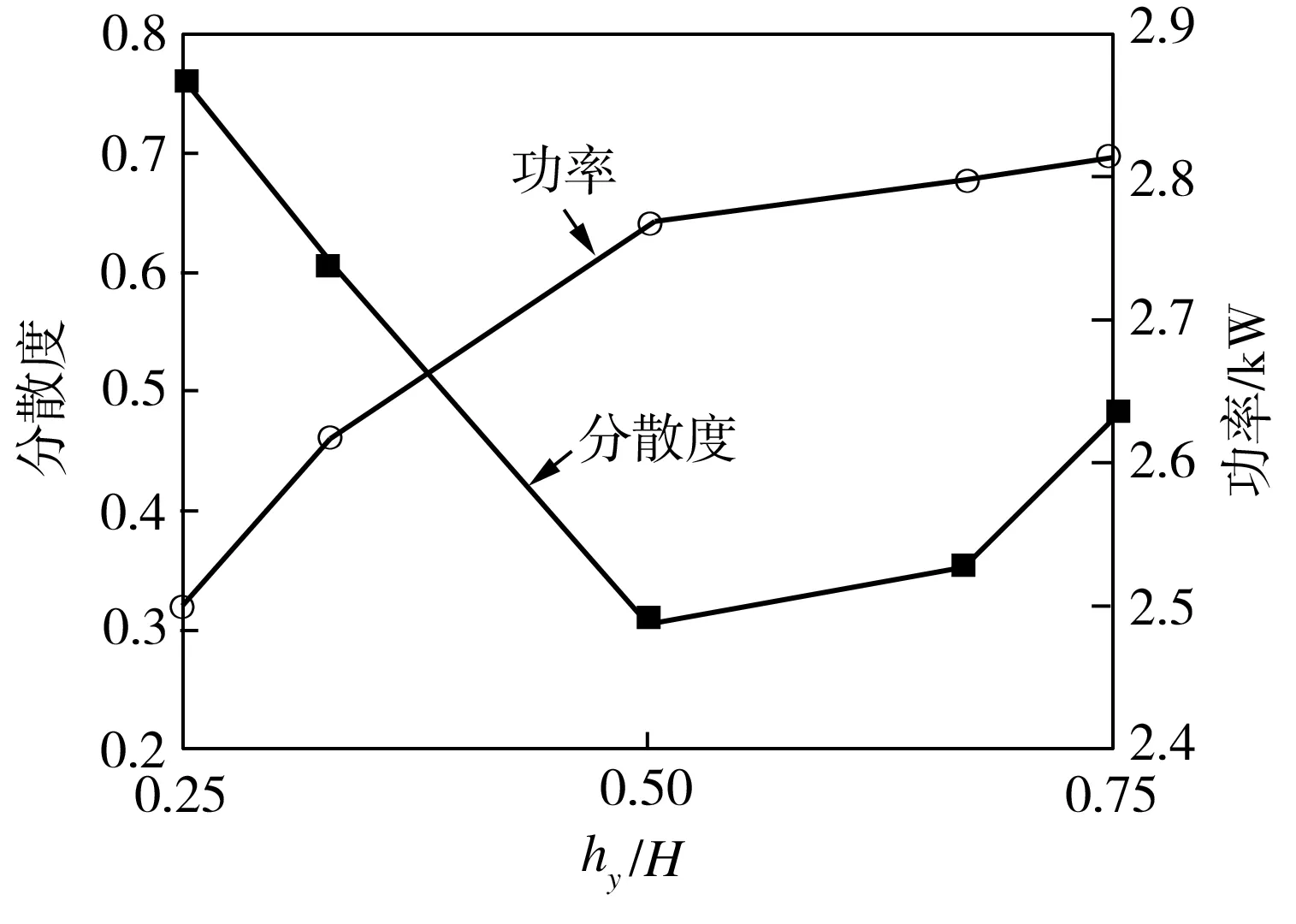
图8 振动混合器中的颗粒分散度及功率消耗

Fig.8Particledispersionandpowerconsumptioninthevibratorymixer

当圆盘直径为0.204 m，与罐底距离为0.1450 m时，不同圆盘振动振幅条件下振动混合器中的颗粒分散度及搅拌消耗功率变化曲线如图9所示。由图9可见，随着圆盘振幅的增大，颗粒分散度不断减小但搅拌混合功率消耗却持续增加，并且颗粒分散度的减幅逐渐变缓而功率消耗的增幅逐渐加大，这表明在考虑功率消耗的情况下应适当调整圆盘振幅以改善颗粒分散度。

图9 不同振幅条件下的颗粒分散度和功率消耗

Fig.9Particledispersionandpowerconsumptionfordifferentamplitudesinthevibratorymixer

当圆盘与罐底距离为0.1450 m，振动振幅为0.05 m时，不同圆盘直径条件下振动混合器中的颗粒分散度及搅拌消耗功率变化曲线如图10所示。由图10可见，当圆盘直径从0.204 m增加到0.260 m时，颗粒分散度显著降低，同时功率消耗在缓慢增加，流场轴向流动有效改善了颗粒分散情况；当圆盘直径超过0.260 m时，颗粒分散度触底反弹且此时功率消耗剧增，这是因为当圆盘直径过大时，圆盘与罐壁之间的距离相比其它模型明显减小，罐内液体轴向流动受阻，圆盘所受作用力变大导致功率消耗剧增。

图10 不同直径条件下的颗粒分散度和功率消耗

Fig.10Particledispersionandpowerconsumptionfordifferentdiametersinthevibratorymixer

2.3 叶轮搅拌器与振动混合器的性能比较

由于叶轮搅拌器与振动混合器的结构和操作方式不同，直接对二者工作效能进行比较存在困难，因此本文基于功率需求对二者性能进行对比分析。叶轮搅拌器和振动混合器的流场压力及速度云图分别如图11、图12所示，综合图11及图12结果表明，叶轮搅拌器中存在环形流动的流场，在其搅拌过程中形成的表面涡速度明显高于罐壁处的流体速度，罐体中心处液面高度低于罐壁面处液面高度，从而将颗粒下拉；而振动混合器中不产生环形流场，主要依靠其中往复式圆盘上下振动产生轴向流动从而下拉颗粒，颗粒在下拉过程中需克服表面张力和浮力，振动混合器的壁面流体速度明显高于中心处的速度，液面在中心处的高度也高于壁面处的相应值，振动混合器通过强烈的流场轴向流动将颗粒向下吸入整个流场。模拟结果显示，当圆盘与罐底间距为0.1450 m、圆盘直径为0.260 m且其振动振幅为0.05 m时，振动混合器中颗粒分散度值最小(见图(10))，相比叶轮式搅拌器中叶轮与罐底间距同为0.1450 m时的颗粒分散度下降了79%，相应功率消耗下降了15%，比叶轮搅拌器获得的颗粒分散度最小值下降了47%，相应功率消耗下降了9%(见图(4))。振动混合器中圆盘振动产生的流场对轻浮颗粒下拉和分散效果更好，在较小的功率消耗下可获得更好的分散度。

(a)叶轮搅拌器 (b)振动混合器

图11流场压力云图

Fig.11Pressurenephogramoftheflowfield

(a)叶轮搅拌器 (b)振动混合器

图12流场速度云图

Fig.12Velocitynephogramoftheflowfield

3 结语

(1)振动混合器与叶轮搅拌器中轻浮颗粒分散的机理不同。叶轮搅拌器依靠中心涡流，借助叶轮产生的液体射流加强径向循环，将颗粒从表面拉入液体中。而振动混合器主要依靠圆盘上下往复运动产生大规模的轴向对称环形旋涡以及流体在圆盘和罐壁间隙处的强烈对流，这种轴向-径向流动将颗粒向下吸入整个流场中。

(2)在叶轮搅拌器中，轻浮颗粒下拉和分散所需功率主要取决于叶轮与罐底间的距离，间距越小，颗粒分散性能越好，但功率消耗较大；而在振动混合器中，当其它因素一定时，颗粒分散度随圆盘振幅增大而不断降低，与此同时，功率消耗逐渐增大；当其它因素一定，圆盘直径超过0.260 m时会降低流场的轴向流动,同时功率消耗会急剧增大；圆盘与罐底距离也是影响颗粒分散性能的重要因素，该间距适中时分散效果最佳。