转子不对中非线性动力学特性研究
2019-04-11马文生李方忠陈平伟李长波李忠刚
马文生,李方忠,陈平伟,李长波,李忠刚
(1.重庆水泵厂有限责任公司总经办, 重庆 400033; 2.重庆机集团博士后科研工作站,重庆 400033;3.北京化工大学 机电工程学院, 北京 100029; 4.哈尔滨工业大学机电工程学院, 哈尔滨 150001)
据有关资料统计表明,约60%的旋转机械振动故障由轴系不对中引起或与之相关[1-6]。随着科学技术的进步和工业不断发展,旋转机械朝着大功率、高转速、高精度、高温和重载的方向发展,由于这些特殊工作环境,对联轴器的功能与作用提出了更新、更高的要求,除了连接两个轴段,传递扭矩和动力外,有时还要求其具有补偿两轴段的相对偏移,起到减振、缓冲的作用,不仅要求提高传动精度及效率,而且要求降低噪声,达到节能的目的,还要优化转子系统工作性能。当连联轴器发生不对中故障时,转子容易发生如下故障:振动过大、轴变形、油膜振荡和轴承损坏等,对转子系统危害较大。随着旋转机械的设计规范和设计要求的提高,转子和静子之间的间隙也逐渐变小,联轴器-转子系统发生不对中故障时,联轴器-转子系统受到的影响也较大[7-13]。
1 不对中力学模型建立
齿式联轴器可以由左套齿和右套齿组成,左半套齿联轴器和右半套齿联轴器设计轴心线和连个套齿的轴心线重合时,转子系统对中较好,这是转子系统轴向不对中力较小,进而不考虑转子的轴向振动,并且齿式联轴器可以对轴向位移进行补偿,可以假设这种情况联轴器-转子系统是对中的。当左半套齿联轴器和右半套齿联轴器设计轴心线和连个套齿的轴心线不重合时,此时联轴器-转子系统有一定的径向不对中量,如图1所示,本文模型只有研究平行不对中引起的非线性动力学问题。

图1 联轴器平行不对中
建立具有联轴器的转子系统动力学方程,需要确定联轴器的模型,简化后联轴器模型如图1所示。联轴器转子系统采用有限元梁单元建模,首先把联轴器-转子系统系统分为若干个节点,每个节点之间采用轴段连接到一起,将轴段和结点分别建立相对应的方程,汇总所有轴段和节点的方程,最终得到整个转子系统的动力学方程。通过选取支承处到联轴器的轴段,并对该部分的齿式联轴器进行等效处理,将左半套齿联轴器和右半套齿联轴器等效为左、右两个节点,假设等效后的左右半套齿联轴器的两个节点为O1和O2,将左、右半联轴器的质量集中到假设的左右半联轴器的两个节点上。由于支承处到联轴器的轴段距离较短,可以认为是刚性轴段,此时左、右两个半联轴器作柱形涡动。转子系统两端支承假设采用弹性支承,其刚度分别取k1和k2。假设联轴器引起的不对中量为δ,在联轴-转子系统高速运转时,齿式联轴器具有一定限位功能,假设左、右两个半联轴器在高速运转过程中,一直保持着不对中量δ。
1.1 联轴器-转子系统的能量方程
1.1.1 联轴器转子系统的系统动能
左、右两个齿式半联轴器的型心坐标是O1(x1,y1)和O2(x2,y2)如图2所示,左边齿式半联轴器存在着一定偏心量e,而右侧齿式半联轴器偏心量为0。假设联轴器-转子系统的转动角速度为Ω,初相位为0,左半联轴器的质心为C1,右半联轴器的型心与质心重合,质心坐标向量分别为:
(1)
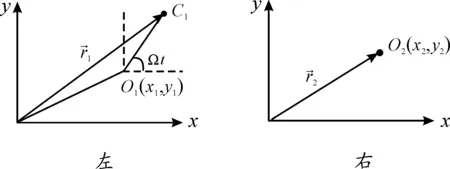
图2 半齿联轴器截面坐标
(2)
故系统的动能为:
(3)
在上式中,左边联轴器在节点处的等效质量为m1,右半联轴器在节点处的等效质量为m2,左半联轴器的转动惯量为J1,右半联轴器的转动惯量为J2,对时间t求导为“·”。
两个半联轴器在运转过程中,一直保持着固定的不对中量δ,故两个半联轴器之间满足约束方程:
(x1-x2)2+(y1-y2)2=δ2
(4)
将型心O2投影到型心O1的平面上,将型心O2的坐标用型心O1的坐标表示,由式(4)得到
(5)
以坐标平面上的型心O1中心,建立相应的动坐标系η、ξ,建立的动坐标系以转子系统的运转角速度Ω围绕着对应的固定坐标系x、y转动,其运转方式如图3所示,得到φ=Ωt+θ,故用x1、y1和θ表示的O2的坐标位置:
(6)
将式(5)代入到式(6)得到系统的动能表达式:
(7)

图3 联轴器型心运转方式
1.1.2 联轴器-转子系统的势能
齿式联轴器和轴段为刚性连接,进而不考虑不考虑其重力势能以及弹性势能,假设联轴器-转子系统两端的支承为弹性支承,其间的轴段运动形式为柱形涡动,获得联轴器的型位移和支承的径向位移具有相同的方向和大小,U表示联轴器-转子系统德势能,联轴器-转子系统的势能只有支承位置的弹性势能,其势能为:
(y1-δsin(Ωt+θ)2]
(8)
1.1.3 系统的耗散能
系统的能量耗散可以用Rayleigh耗散函数ψp表示:
(9)
在式中,左齿式半联轴器的黏性阻尼系数为c1,右齿式半联轴器的黏性阻尼系数为c2。
将式(5)代入式(9)得到O1的坐标和θ表示Rayleigh耗散函数ψp:
(10)
1.2 不对中动力学方程
运用拉格朗日方程,考虑系统存在不平衡力,由此得到系统的动力学微分方程组:

(11)

(12)
由z=A-1F可以得到方程:
(13)
联轴器的结构通常为对称式,假设质量m1=m2=m,左半齿半联轴器刚度等于右半齿联轴器的刚度,令k1=k2=k,假设左半齿联轴器存在一定阻尼,而右半齿联轴器不存在黏性阻尼,c2=0,c1=c,令x1=x、y1=y。获得式(13),得:
(14)
对联轴器的动力学方程进行无量纲化处理,令X=x/δ、Y=y/δ、τ=Ωt,式(14)化为:
(15)
式中,X′、X″、Y′、Y″、θ′、θ″分别表示对τ的一阶、二阶导数。
2 不对中和不平衡对系统响应的影响


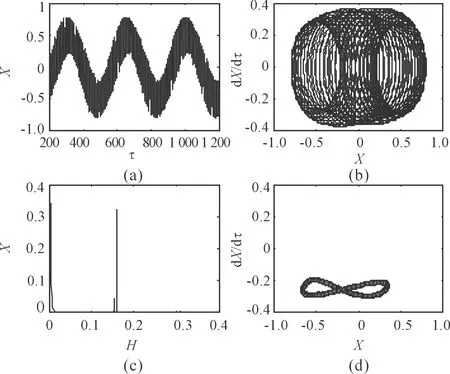
图时X响应图

图5 X的幅值谱图
3 结论
带有联轴器的转子系统在低转速运转,转子系统不平衡量激起的不平衡力和不对中激起的不对中力共同作用于转子系统,其运动形式为拟周期运动,转子不平衡量引起的激励力随转速增大而增大,而不对中激起的不对中力影响逐渐变小,联轴器-转子系统变为以基本为主的单周期运动形式。联轴器-转子系统的响应也与不平衡量和不对中比值有关,当不对中和不平衡的比值较大时,联轴器不对中对转子系统的影响明显,当不平衡量和不对中量的比较大时,不平衡对转子系统的影响明显。
