幂零群与内幂零群的幂图
2019-01-08郭秀云
郑 涛,郭秀云
(上海大学理学院,上海200444)
幂图是通过群G的幂结构定义的图,即以群的全部元素作为图的顶点,不同顶点x与y有边相连当且仅当x=ym或y=xm,其中m∈N∗.幂图最早是在2002年由Kelarev和Quinn在半群中研究的,即半群中的不同元素x与y存在弧x→y当且仅当y=xm,其中m∈N∗[1].对于抽象有限群,2009年Chakrabarty等[2]开始考虑乘法半群Zn和其单位群Un的幂图,并决定了其为完全图、可平面图以及Hamilton图的条件.2010年,Cameron[3]证明了两个有限群无向幂图同构与有向幂图同构等价.此外,2011年Cameron等[4]证明了有限交换群的幂图同构则群同构.考虑到幂零群、内幂零群以及内交换群在有限群研究中的重要地位,研究这三类群的幂图在一定程度上有助于人们进一步研究一般有限群的幂图结构以及群与图的关系.本工作基于2013年Chelvam等[5]关于有限交换群幂图的研究和2015年Doostabadi等[6]以及Pourgholi等[7]关于幂零群真幂图研究的一系列相关成果,对上述三类群的幂图性质与结构进行探究.
本工作主要是研究幂零群、内幂零群以及内交换群所对应幂图的一系列图论性质.由于这类群结构比较清晰,可以对其相应幂图或真幂图的性质作进一步研究,主要从能否为线图、独立数性质、可平面性以及连通性等角度讨论.特别地,由于一般群G的任意元素都与单位元相连,故在考察连通性时仅对真幂图P∗(G)进行讨论.
1 准备工作
假定本工作中出现的群皆为有限群,所用到的一系列符号与定义如下.V(Γ),E(Γ)分别表示图Γ的顶点集合与边集合.设G为有限群,用P(G)以及P∗(G)分别表示群相应的幂图与真幂图,其中真幂图是幂图去掉单位元顶点后所诱导的子图.K5为5个点的完全图,K3,3为由两个含3个元素的集合构成的二部图.此外,设Γ1,Γ2为两个图,则Γ1∪Γ2表示以V=V(Γ1)∪V(Γ2)为新的顶点集,以 E=E(Γ1)∪E(Γ2)为新的边集所得到的图;Γ1+ Γ2表示在Γ1∪Γ2的基础上还满足Γ1中所有点与Γ2中所有点相连的图.图Γ的线图L(Γ)是一个图,其全部顶点是Γ的所有边并且当边e=uv和f=vw在Γ中出现时才有ef∈E(L(G)).图Γ中一个顶点子集合称为是独立的,如果该集合中任意两顶点都不邻接.图Γ的点独立数β(Γ)定义为Γ中点独立集的最大基数.图Γ称为一个平面图,如果Γ能够画在一个平面上而使得任何两条边都不会交叉.对于图Γ中的两点x与y,用x~y表示两个不同顶点有边相连,用x≃y表示两顶点或者x=y或者x~y,用x/~y表示顶点不相连,d(x,y)表示两顶点间距离.此外,diam(Γ)表示图Γ的连通直径,k(Γ)表示其连通分支个数.设群G为p群,s1(G)表示其p阶子群的个数.下面给出主要应用的引理.
引理1[8]图G是某图的线图当且仅当图G不具有图1中9种形式的诱导子图.
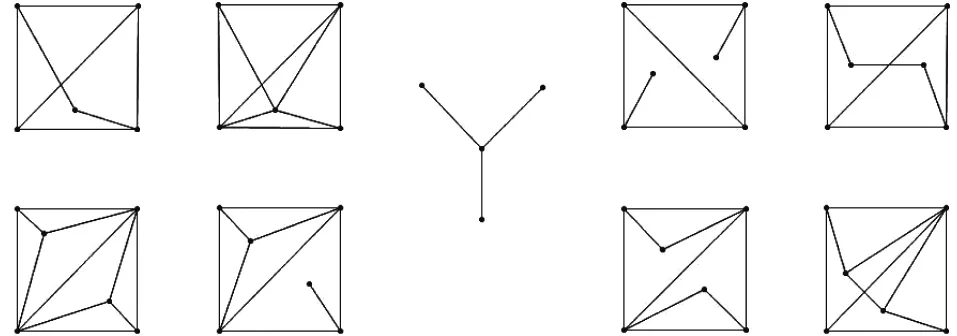
图1 9种诱导子图Fig.1 9 induced subgraphs
引理2[2]设G是有限群,则其幂图P(G)是完全图当且仅当G为pm阶循环群,其中p为素数,m∈N.
引理 3[5]设G为群,且|G|=,其中p1,p2,···,pn是一些互不相同的素数,则群G的独立数β(P(G))≥n.
引理4[8]K5和K3,3是不可平面图.
引理5[9]设G是有限群,则其幂图P(G)可平面化当且仅当每个元素的阶属于集合{1,2,3,4}.
引理6[6]设G是有限p群,则其真幂图P∗(G)的连通分支与G的p阶子群一一对应.
引理7[10]设G是内幂零群,则G有下列性质:
(1)|G|=pnqm,p/=q均为素数,且适当选择符号便有G的Sylow p-子群PG,而Sylow q-子群循环,故QG,并有Φ(Q)≤Z(G);
(2)Φ(P)≤Z(G),特别地c(P)≤2;
(3)若p>2,则exp(G)=p,而若p=2,则exp(P)≤4.
2 主要结果
下面分别对幂零群、内幂零群以及内交换群的幂图或真幂图进行讨论.一般地给出了有限群的幂图为某图之线图的充要条件,研究了相应幂图独立数的临界取值与可平面化的充要条件以及相应真幂图的连通性.
定理1 设G为有限群,则幂图P(G)是某图的线图当且仅当G为素数幂阶循环群.
证明 必要性:设有限群G的幂图P(G)是某图的线图,下面分三步证明结论.
(1)群G的Sylow子群皆循环.设P为Sylow p-子群,由p群的计数定理(见文献[11]中定理8.8)可知p阶子群的个数s1(G)≡1(mod p).若s1(G)/=1,则s1(G)≥1+p≥3.取x,y,z∈G分别为3个不同p阶子群的生成元,幂图P(G)在顶点子集H={1,x,y,z}上诱导的子图P(H)为爪形图,由引理1知不可能是某个图的线图,矛盾.故P有唯一极小子群,从而P是循环群或者广义四元数2群(见文献[10]中定理5.7.1).若群G=〈a,b:a2n-1=1,b2=a2n-2,b-1ab=a-1〉为广义四元数2群,幂图P(G)在顶点子集K={1,a,b,ba}上诱导爪形子图P(K),即P(G)不是线图,从而P为循环群.
(2)群G的Sylow子群皆正规.若否,存在一个Sylow子群不正规,不妨设PG,此时群G的Sylow p-子群的个数np≥1+p≥3,取x,y,z为3个不同的循环Sylow p-子群的生成元,则子集合M={1,x,y,z}在幂图P(G)中诱导的子图P(M)为爪形图,即P(G)不是某个图的线图,矛盾.
必要性得证.
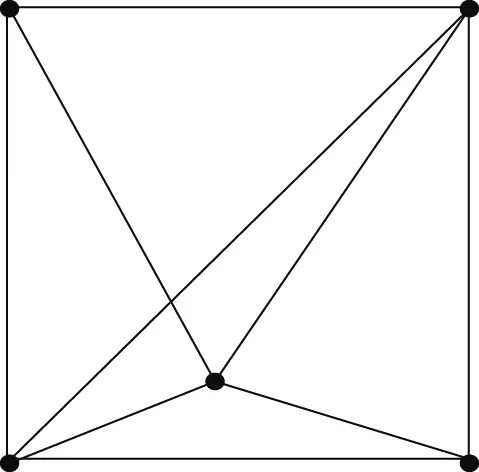
图2 诱导子图P(N)Fig.2 Induced subgraph P(N)
充分性:若G是素数幂阶循环群,由引理2知幂图P(G)为完全图,自然可看作星图K1,|G|的线图,充分性显然.
定理 2 设幂零群G=P1×P2×···×Pn,其中Pi为群G的Sylow pi-子群,则其幂图P(G)的独立数β(P(G))=n当且仅当G为阶是p1p2p3或p1rp2或pr1的循环群,其中pi(i=1,2,3)均为素数,r∈N.
证明 必要性:由于G有n个不同的素因子,由引理3可知幂图P(G)必存在含有n个元素的点独立集.又已知β(P(G))=n,则群G的每个Sylow p-子群皆为循环群.设,当n≥4时,在集合{g∈G:o(g)=pipj,1≤i,j≤n,i/=j}中即可找到含n+1个元素的点独立集,矛盾.从而n≤3.当n=1时,因为β(P(G))=1,G必为素数幂阶循环群;当n=2时,若r1,r2≥2且o(x)=,o(y)=,则有{x,y,xp1yp2}为G的势为3的点独立集,矛盾,从而至多只有一个素因子幂指数大于等于2,即|G|=;当n=3时,应用前述方法可知|G|=若r1≥2,设o(x)=,o(y)=p2,o(z)=p3,则有{xp1y,xp1z,x,yz}为一个势为4的点独立集,矛盾,从而|G|=p1p2p3.
充分性:若G为阶是p1p2p3或的循环群,下面依次讨论.
(1)当|G|=p1p2p3时,P(G)~=K1+(Kϕ(p1p2p3)+K),其中K如图3所示,可以验证独立数β(P(G))=3;
(2)当|G|=p1rp2时,Γ=K1+(Kpr1-1∪Kpr1(p2-1))是P(G)的子图且β(Γ)=2.又子图Γ的顶点集V(Γ)=V(P(G)),边集E(Γ)⊆ E(P(G)),则β(P(G))=2;
(3)当|G|=pr1时,P(G)~=Kpr1为完全图,独立数β(P(G))=1.
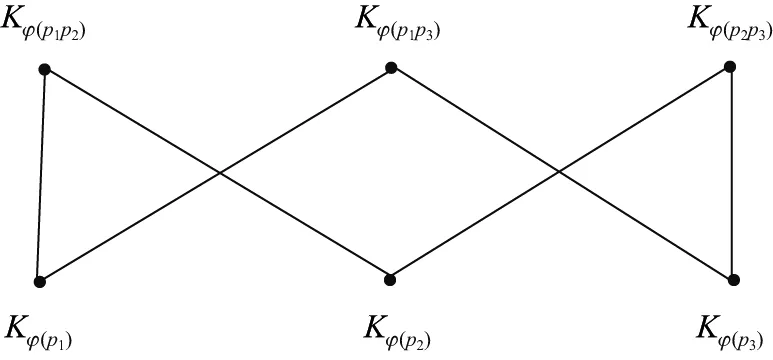
图3 抽象图KFig.3 Abstract graph K
定理3 幂零群G的幂图P(G)可平面化当且仅当群方次数exp(G)=3或exp(G)整除4.
证明 必要性:若有限群G的幂图P(G)可平面化,由引理5可知群元素的阶只能取自集合{1,2,3,4}.又G幂零,则G只能为2群或3群,故有exp(G)=3或exp(G)整除4.
充分性:若exp(G)=3,作出其幂图P(G)~=K1+lK2;若exp(G)整除4,其幂图为P(G)~=K1+(mK1∪nK3),其中l,m,n∈N,显然二者均可平面化.
定理4 内幂零群G=PQ,其中P为正规Sylow p-子群,Q为循环Sylow q-子群(见引理7),则其幂图P(G)可平面化当且仅当G为以下情形之一:
(1)G是Frobenius群且满足P为初等交换2群,Q为3阶循环群;
(2)G是Frobenius群且满足P为初等交换3群,Q为2阶循环群.
证明 必要性:由于内幂零群G的幂图可平面化,由引理5可得{p,q}={2,3}.
Case 1.p=2,q=3.先证明CP(Q)=1.若否,则可取x∈CP(Q),o(x)=2与y∈Q,o(y)=3,显见子群H=〈x〉×〈y〉诱导的子图P(H)含有K3,3,由引理4可知不可平面化,矛盾.此时P为初等交换2群,又由于Q为3阶循环群,故Q在P上作用为无不动点自同构,即G为Frobenius群.
Case 2.p=3,q=2.先证明|Q|=2.若否,显然|Q|=4,可取x∈P,o(x)=3与y∈Q,o(y)=4,因G内幂零,则有子群H=〈x〉×〈y2〉诱导的子图P(H)含有K3,3,从而可得幂图不可平面化,矛盾.故|Q|=2,类似Case 1可以证明CP(Q)=1,则有P为初等交换3群且G为Frobenius群.
充分性:命题中两种情形相应的幂图P(G)~=K1+(mK1∪nK2),其中m,n∈N,从而可平面化.
定理5 有限群G=PQ为内幂零群,其中P为正规Sylow p-子群,Q为循环Sylow q-子群.设|G|=pnqm,则其真幂图P∗(G)的连通性有如下结论.
Case 1.m≥2,真幂图P∗(G)连通且满足:
(1)若P是循环群或广义四元数2群,diam(P∗(G))≤3;
(2)若P既不循环也不是广义四元数2群,diam(P∗(G))≤4.
Case 2.m=1,设 Q= 〈a〉,真幂图 P∗(G)满足:
(1)若CP(a)=1,则P∗(G)不连通且连通分支个数k(P∗(G))=
(2)若CP(a)>1,则P∗(G)的连通分支个数为k(P∗(G))=s1(P)-s1(Φ(P))+1.
证明 Case 1.m ≥ 2,设Q= 〈a〉,令Q1= 〈aq〉,则G1=P ×Q1幂零,根据文献[6]中定理2.6可知,其真幂图连通且满足若P是循环群或广义四元数2群,diam(P∗(G1))=2;若P既不是循环群也不是广义四元数2群,diam(P∗(G1))=4.任取不同两点g1,g2∈G,下面在两种情形下讨论真幂图P∗(G)的连通性.
(1)P是循环群或广义四元数2群.若p∈π(o(g1))π(o(g2))则存∩在m1∈N∗使得o()=p满足g1≃≃ g2,即 d(g1,g2)≤ 2;若q∈ π(o(g1))π(o(g2))则存在m2,m3∈N∗满足o()=q.由Q1的正规性可知其包含在群G的任意一个Sylow q-子群中,从而,即d(g1,g2)≤2.若g1为p元素,g2为q元素,当o(g2)<qm时,构造g1~g1g2~g2;当o(g2)=qm时,构造,故d(g1,g2)≤3.综合上述3种情况可知d(g1,g2)≤3.∩
(2)P既不是循环群也不是广义四元数2群.若q∈π(o(g1))π(o(g2)),由(1)可知d(g1,g2)≤2.若g1是p元素且q∈π(o(g2)),存在m4∈N∗使得1<o()<qm,则g1~≃ g2,即d(g1,g2)≤ 3.若g1,g2均为p元素,g1~ g1µ ~ µ(∈ Q1)~ g2µ ~ g2.综合上述3种情况可知d(g1,g2)≤4.
故内幂零群真幂图P∗(G)连通且直径diam(P∗(G))≤3或4.
(1)CP(a)=1,则〈a〉为P的无不动点自同构群,从而G为Frobenius群,且Φ(P)=CP(a)=1,此时P初等交换群且G=.故易得其真幂图P∗(G)的连通分支数:
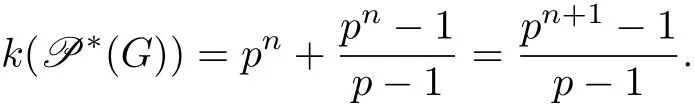
(2)CP(a)/=1,考虑商群G=G/Φ(P)=P/Φ(P)(〈a〉Φ(P))/Φ(P),则由文献[10]中定理其中l=|P|.进而有 G=P Φ(P)QΦ(P)Qh2··· Φ(P)Qhl.又Φ(P)=CP(a)/=1,顶点集连通且连接P中与Φ(P)相连的顶点,故P∗(G)的连通分支个数为k(P∗(G))=s1(P)-s1(Φ(P))+1.
定理6 设内交换群G=PQ,其中P为正规Sylow p-子群,Q为循环Sylow q-子群,|G|=pnqm,则其幂图P(G)的独立数β(P(G))≥q+1且等号成立当且仅当以下情形之一成立:
(1)当m≥2时,Sylow q-子群个数为q+1;
(2)当m=1时,G ~=S3或G为2n(2n-1)阶Frobenius群,其中Sylow 2-子群正规,2n-1为素数.
证明 对于G=PQ,考虑Q在P上的作用,则有P=CP(Q)×[P,Q](见文献[10]中定理8.2.7).若CP(Q)>1,则[P,Q]<P,从而G交换,矛盾.故CP(Q)=1,P是初等交换p群,取P中的p阶子群的生成元代表A={x1,x2,···,xt},其中t=又循环群Q非正规,由Sylow第三定理可知其Sylow q-子群的个数至少∪为q+1,取出这q+1个循环群的生成元代表B={y1,y2,···,ys},其中s=q+1,显然AB即构成了势为q+1的点独立集,不等式显然成立.下面考虑等号成立条件.
必要性:若m ≥2,由于Sylow q-子群的个数nq≥q+1,若不等号严格成立,用上述方法可以得到势至少为t+2q+1的点独立集,矛盾,即nq=q+1.若m=1,由CP(Q)=1可知Q在P上的作用是无不动点的,此时G为Frobenius群,相应的Frobenius分划为 〉取点独立集D={x1,···,xt,y,yg2,···,yg|P|},若要使等号成立必须有 t+|P|≤ t+q+1,又 q+1||P|,故得|P|=q+1,若p是奇素数,显然q=2,|P|=3,此时G为非交换的6阶群,即G~=S3.若p=2,则有q=2n-1为素数,此时G为2n(2n-1)阶Frobenius群.
充分性:当m≥2时,群G中不存在阶为pαqm(α/=0)的元素,若否,则与CP(Q)=1矛盾. 设集族容易验证任意g∈G都属于该集族中某个元素.对于S的子族至多可选择 t个群 G 中元彼此不相连. 若否,存在 g1/~ g2且不妨设〉均为 Sylow q-子群, 存在g=,u ∈ N,a ∈ P, 使得 〈y2〉= 〈y1〉g= 〈y1〉a,即存在 v ∈ N,y2=y1av, 此时〉.又 c≡ 1(mod p),c≡ v(mod qm-1),由孙子定理[13]可得 c有解,故因o(g1),o(g2)有整除关系,则g1∪~ g2,矛盾.从而等号恒成立.当m=1 时,若 G ~=S3,则其幂图 P(G) ~=K1+(3K1K2),则有 β(P(G))=4.若G为2n(2n-1)阶Frobenius群,其中Sylow 2-子群正规,q=2n-1为素数,此时P(G)~=K1+(qK1(q+1)Kq-1),则有β(P(G))=2q+1.从而两种情形均可取到等号,命题得证:
定理7 设群G内交换,则其幂图P(G)可平面化当且仅当以下情形之一成立:
(1)G=PQ是Frobenius群且满足P为初等交换2群,Q为3阶循环群;
(2)G=PQ是Frobenius群且满足P为初等交换3群,Q为2阶循环群;
(3)exp(G)=4时有G=Q8,M2(2,1),M2(2,2),M2(2,1,1)或M2(2,2,1);
(4)exp(G)=3时有G=M3(1,1,1).
证明 若内交换群G=PQ,则G内幂零,此时由定理4可得G有形式(1),(2).下面考虑G为p群.由引理5得可平面化群的元素之阶取自集合{1,2,3,4},故p=2或p=3.由内交换群的分类(见文献[14]中定理2.3.7)可知,G=Q8或G=Mp(n,m),n≥2,m≥1或G=Mp(n,m,1),n≥m≥1按方次数讨论:当exp(G)=4时群的可能形式有G=Q8,M2(2,1),M2(2,2),M2(2,1,1)或M2(2,2,1);当exp(G)=3时群的可能形式有G=M3(1,1,1);当exp(G)=2时群的可能形式有G=M2(1,1,1).下面逐一验证上述形式群幂图的可平面性.
Case 1.由定理4可知(1),(2)中群的幂图显然可平面化.
Case 2.当G=Q8或G=M2(2,1)=D8时,显然方次数exp(G)=4可平面化.当G=M2(2,2)时,元素(biaj)4=b4ia(4+12i)j=1;当G=M2(2,1,1)时,元素(aibjck)4=(aibj)4=a4ib4j[b,a]6ij=1,从而其幂图可平面化.同理M2(2,2,1)幂图可平面化.
Case 3.当G=M3(1,1,1)时,元素(aibjck)3=(aibj)3=a3ib3j[b,a]3ij=1,幂图可平面化.
Case 4.当G=M2(1,1,1)=D8时,exp(G)=4/=2,矛盾.
综上可知,命题得证.
定理8 有限群G为内交换群,则其真幂图P∗(G)的连通性有如下结论.
(1)若m≥2,则P∗(G)连通且diam(P∗(G))≤4;
(2)若m=1,则P∗(G)不连通,连通分支个数k(P∗(G))=
Case 2.G为内交换p群,则真幂图P∗(G)满足:
(1)若G=Q8,则P∗(G)连通且diam(P∗(G))=2;
(2)若G=Mp(n,m),n≥ 2,m ≥ 1.当G/=M2(2,1)时,P∗(G)连通分支个数k(P∗(G))=p+1.当 G=M2(2,1)时,k(P∗(G))=5;
(3)若G=Mp(n,m,1),n≥m ≥1.当G/=M2(1,1,1)时,P∗(G)连通分支个数k(P∗(G))=p2+p+1.当G=M2(1,1,1)时,k(P∗(G))=5.
证明 对内交换群G分为非p群与p群两种情形讨论.
Case 2.G为内交换p群.根据文献[14]中定理2.3.7可得G仅有Q8,Mp(n,m)n≥2,m≥1,Mp(n,m,1)n≥m≥1这3种情形.
(1)若G=Q8,其真幂图P∗(G)=K1+3K2,显然连通且满足diam(P∗(G))=2;
(2)若G=Mp(n,m),此时G={biaj:ab=ba1+pn-1},|G|=pn+m,故知biaj两两不同.容易计算
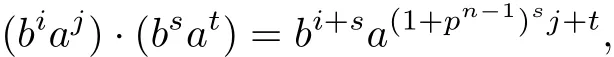
利用上式求G的p阶元,则有
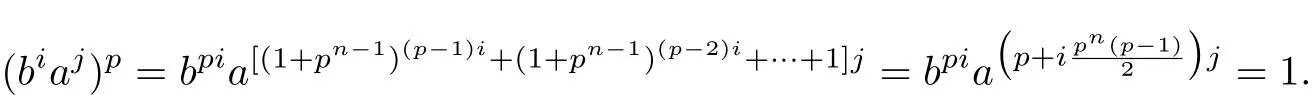
①m ≥ 2,于是得pm|pi,即pm-1|i,i.e.i=pm-1,2pm-1,···,pm,故bi∈ Z(G),此时(biaj)p=bipajp=1,即j=pn-1,2pn-1,···,pn,从而易得p阶元的个数为p2-1,p阶子群个数为p+1.由引理6可知P∗(G)的连通分支个数k(P∗(G))=p+1.② m=1,此时G=Mp(n,1)= 〈a,b:apn=bp=1,ab=a1+pn-1〉,容易计算
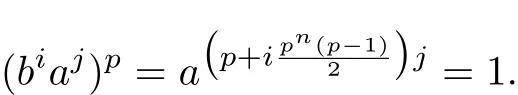
若p为奇素数,即apj=1,于是j=pn-1,2pn-1,···,pn,i=1,2,···,p.此时G有个p阶子群,真幂图P∗(G)不连通且k(P∗(G))=p+1.若p=(a)当i=0时,(biaj)2=a2j=1可得2阶元为a2n-1;(b)当i=1时,2n|j(2+2n-1),若2 ł j得到2n|2+2n-1,此时仅有n=2时成立,群G为M2(2,1)即二面体群,若2|j得到a2j=1,此时2阶元为ba2n-1,b.故可得当G/=M2(2,1)时k(P∗(G))=3;当G=M2(2,1)时k(P∗(G))=5.
(3) 若 G=Mp(n,m,1)则 G′= 〈c〉,G={aibjck:i=1,2,···,pn;j=1,2,···,pm;k=1,2,···,p},其中c∈ Z(G).设aibjck为G的一个p阶元,则有(aibjck)p=(aibj)pckp=(aibj)p=1,由于
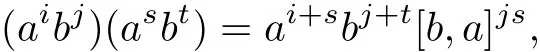
利用上式可得
故可得i=pn-1,2pn-1,···,pn,j=pm-1,2pm-1,···,pm.当 n ≥ 2或 m ≥ 2时,G 的 p阶元 aibjck满足 i=pn-1,2pn-1,···,pn,j=pm-1,2pm-1,···,pm,k=1,2,···,p,且 i,j,k不同时取pn,pm,p.故真幂图P∗(G)的连通分支个数k(P∗(G))=+p+1.当n=m=1时,可得(aibj)p=apibpj[b,a]p(p2-1)ij=[b,a]p(p2-1)ij=1,若p≥3,同上,G有p3-1个p阶元,即连通分支个数k(P∗(G))=p2+p+1.若p=2,则G=M2(1,1,1)=D8,k(P∗(G))=5,命题得证.
3 结束语
本工作讨论了幂零群、内幂零群以及内交换群和它们相对应幂图的关系问题,主要从线图、独立数、可平面性以及连通性等图论性质出发进行研究.一般地得到了有限群G的幂图P(G)是某图的线图的充要条件,刻画了幂零群与内交换群独立数的临界情形以及3类群可平面化的充要条件.此外,给出了内幂零与内交换群真幂图连通时的连通直径估计以及不连通时连通分支数目计算.对于这3类特殊的有限群幂图的图论性质给出了清晰的描述.相反地,也从相应幂图的图论性质出发进一步刻画了群结构.
