长杆弹侵彻半无限混凝土靶的理论研究
2019-01-08卢正操张元迪文鹤鸣李名锐钱秉文
卢正操,张元迪,文鹤鸣†,周 刚,李名锐,钱秉文
(1.中国科学技术大学中国科学院材料力学行为和设计重点实验室,合肥230027; 2.西北核技术研究所,西安710024)
混凝土结构被广泛应用于国防和土木工程中,经常受到不同形式载荷的作用,尤其是在军事防护工程中,混凝土防护结构可能会受到各种弹体冲击及爆炸载荷的作用。因此,研究混凝土结构的侵彻问题对于防护结构的安全计算和安全评估均具有重要意义。Forrestal等对刚性弹侵彻半无限混凝土靶进行了实验研究[1-5],采用钢卵形弹以不同速度侵彻水泥砂浆和混凝土靶,当弹体的冲击速度v0小于1 300 m·s-1时, 弹体的质量损失在8%之内,且弹体的侵彻深度随冲击速度的增大而增大。Gold等利用无氧铜(OFHC)和钽材料制成的球头长杆弹以冲击速度为1 500~1 900 m·s-1侵彻混凝土靶,给出了弹体的残余质量与侵彻深度的时程曲线[6]。Nia等利用铜锥头弹以冲击速度为650~1 200 m·s-1侵彻半无限混凝土靶[7],结果表明:虽然在侵彻过程中,弹体存在少量的质量损失,但其依旧可被视为变形弹。Mu等利用38CrSi钢卵形弹以冲击速度为500~1 500 m·s-1侵彻混凝土靶[8],实验结果表明,当弹体的冲击速度大于一个临界值时,弹体的侵彻深度急剧减小,弹头形状从卵形变成半球形,弹体从刚体侵彻状态过渡到变形侵彻状态甚至是销蚀侵彻状态。Kong等对洛氏硬度为11.5~11.9的45#平头钢弹侵彻砂浆靶进行了一系列实验[9], 弹体的冲击速度范围为510~1 850 m·s-1。实验结果表明, 当弹体的冲击速度大于997 m·s-1时,弹体开始发生销蚀;当冲击速度小于1 373 m·s-1时,弹体以变形状态侵彻混凝土靶,此时弹体的形状类似于酒瓶状[9]。与长杆弹高速侵彻金属靶[10]一样,实验中也观察到了由弹体冲击速度决定的3种侵彻模式。

本文基于长杆弹侵彻半无限金属靶的理论[19-25],对长杆弹以不同冲击速度侵彻半无限混凝土靶进行了研究,得到了长杆弹侵彻混凝土靶不同侵彻模式间的临界转化条件及相应的参数计算方程,并将模型计算结果与文献中的相关实验数据进行了比较分析。
1 混凝土统一侵彻模型
根据弹体动态强度Yp和混凝土靶静阻力a0的相对大小,将长杆弹对半无限混凝土侵彻分为Yp≤a0和Yp>a0两种情况。
1.1 Yp≤a0
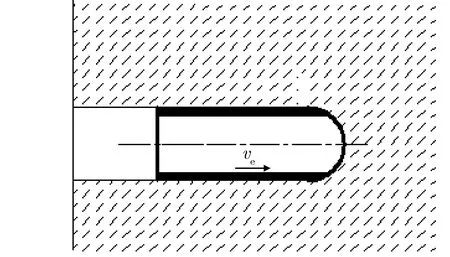
当Yp≤a0,且v0>vid时,弹体以销蚀状态侵彻混凝土靶。侵彻时,弹体头部形成蘑菇头,同时向后抛射的弹体销蚀碎片呈圆管状。受弹体侵彻速度、弹靶密度及弹体强度等因素的影响,由向后抛射的弹体销蚀碎片形成的空心圆管可能会对混凝土靶体进行二次侵彻[24]。
当弹体的侵彻速度u大于临界速度uf0时,弹靶附近的材料会产生极大的静水压,因此可以忽略靶体材料的剪应力,此时弹靶界面材料可以看成近似流体(此为A-T模型的基本假设)。基于文献[19,20-21,25]的研究,本文认为长杆弹侵彻混凝土靶体时,靶体的响应区与金属靶板的响应区类似,同样可以划分为流动区、塑性区(包括破碎区和开裂区)和弹性区。图1为长杆弹侵彻半无限混凝土靶示意图。

(a)Response regions in the target

(b)Rosive penetration

(1)
式中,n为参数,通常n=3[19]。弹体顶点O的压力可由修正的Bernoulli方程计算得到[19]:
当u≥uf0时,
(2)
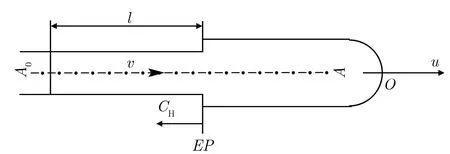
当u (3) 式中,ρp为弹体密度;σr(u)为空穴表面的径向应力,可利用动态球形空穴膨胀理论计算得出[16]: σr(u)=a0+a1u+a2u2 (4) 式中,a1,a2为拟合的动阻力参数。在销蚀侵彻过程中,弹体的销蚀速率和减加速度可以表示为 (5) (6) (7) 式中,vid定义为当Yp≤α0时,弹体侵彻靶体的最小速度,即,当冲击速度低于该临界速度时,弹体不能侵彻靶板,此时弹体行为类似于泰勒圆柱撞击。u=0时,可以得到: (8) 此时的u~v关系可以通过式(1)--式(4)确定。 弹体残余长度Lres,h可表示为 (9) 式中,L0为等效弹长,是将弹体等效为质量及横截面积均相同的平头弹长度,mm。 当ρp>ρt,且冲击速度足够高时,在销蚀侵彻过程中,弹体形成的销蚀碎片将沿中轴线向前运动并且继续侵彻靶体。图2给出了弹体以冲击速度v0撞击靶体时,弹体向后抛射的销蚀碎片形成的圆管二次侵彻靶体的示意图。此时,弹体已完全销蚀。 图2弹体向后抛射的销蚀碎片形成的圆管二次侵彻靶体示意图Fig.2 Debris tube penetrating the target when a penetrator is completely eroded 销蚀碎片形成的圆管动态强度Ytub为0,销蚀碎片形成的圆管二次侵彻靶体的侵彻深度为[24] (10) 式中,ve为弹体向后抛射的销蚀碎片速度;ue为v=ve时,所对应的侵彻速度;ve可通过式(11)计算得出: ve=φ(v-u)-u (11) 式中,φ可以表示为 (12) Ltub是销蚀碎片形成的圆管的长度,可通过式(13)确定: Ltub=φ(L0-Lres,h) (13) 式(10)中,α为等效密度因子,可由式(14)给出[24]: (14) 式中,ρave为销蚀碎片形成的圆管的平均密度;Rm为弹体蘑菇头半径;r0为弹体初始半径。Rm与r0之比为[22] (15) 其中,p(θ)可以通过将式(1)--式(4)中的u替换为ucosθ计算得到。 由此,当Yp≤α0,弹体的总侵彻深度表示为 Ptot=Ppri+Psec (16) 当Yp>a0时,根据冲击速度的不同,弹体侵彻混凝土靶体有刚体侵彻、变形非销蚀侵彻和销蚀侵彻3种侵彻模式。本文给出3种侵彻模式的求解方程,并确定3种不同侵彻模式之间转换的刚体速度vr和流体动力学速度vh两个临界速度。 1.2.1刚体侵彻 当v0较低时,由于Yp>a0,弹体以刚体状态侵彻靶体,弹体不会发生变形或钝粗。 图3为卵形弹头侵彻半无限混凝土靶体的示意图。 图3卵形弹侵彻半无限混凝土靶体的示意图Fig.3An ogival-nosed rigid projectile penetrating a semi-infinite concrete targets (17) 当vcosφ0≥uf0时,存在一个临界角度φc,使得vn=vcosφc=uf0;当vcosφ0 (18) p(φ)=σr(vn),φc≤φ≤π/2 (19) 式中,vn=vcosφ为侵彻速度沿卵形弹圆弧表面的法向速度分量,对于一个给定的弹头形状,如卵形弹,其所受的靶体合力F(r0,v)与Ψ,r0及v有关: (20) 因此,刚体侵彻时,弹体的侵彻深度为 (21) 式中,m为卵形弹的初始质量。 本文提出的刚体侵彻模型是在文献[16]提出的模型基础上改进的。当vcosφ0 1.2.2变形非销蚀侵彻 图4为长杆弹变形非销蚀状态示意图。从图中可以看出弹体变形非销蚀侵彻半无限混凝土靶体的初始状态和变形状态。图中,A0为弹体未变形的横截面积;A弹体变形后的横截面积;L为初始弹长;EP为弹体变形部分与未变形部分的界面;CH为界面EP相对于O点的运动速度。 (a)Initial state (b)Deforming non-erosive state 如果v0满足vr Ptot=Pdef+Pres,r (22) 式中,Pdef为弹体在变形非销蚀状态的侵彻深度;Pres,r为残余弹体以刚体状态侵彻的深度。 由质量守恒和动量守恒定理可以得到: (v-u+CH)A0=CHA (23) (v-u+CH)A0ρp(v-u)= F(rd,u)-YpA0= f(u)A-YpA0 (24) 式中,F(rd,u)为弹头所受阻力的合力,可通过式(20)得到。rd为弹体变形后的横截面半径。弹体未变形部分的长度变化以及加速度可表示为 (25) (26) 联立式(23)-式(26),得到弹体变形非销蚀状态下的u~v关系为 (27) 因此,弹体以变形非销蚀状态侵彻混凝土靶的侵彻深度可以表示为 (28) (29) 因此,残余弹体的总长度为 (30) (31c) 式中,a,b为实验拟合参数;vc为式(31a)值与式(31b)值相等时所对应的弹体冲击速度。常数c可通过文献[22]中长杆弹侵彻半无限靶的理论确定。 1.2.3销蚀侵彻 当v=vh时,弹体的侵彻模式从销蚀侵彻转变为变形非销蚀侵彻,弹头半径不再变化且与v0=vh时的弹头半径相同;当v=vr时,弹体由变形非销蚀状态转变为刚体状态,并以刚体状态继续侵彻混凝土靶体直到侵彻过程结束。此时,弹体总侵彻深度为 Ptot=Ppri+Pdef,r+Pres,r+Psec (32) 式中,Ppri为弹体销蚀侵彻的侵彻深度;Pdef,r为残余弹体在变形非销蚀状态下的侵彻深度;Prig,r为 弹体刚体状态下的侵彻深度。Ppri可以通过将式(7)中的vid替换成vh得到: (33) 销蚀侵彻阶段,弹体的u~v关系与Yp<α0时的关系相似。当销蚀侵彻结束时,残余弹长Lres,h的计算公式为 (34) 计算Pdef,r的公式与式(28)类似,只需将其积分上限v0替换为vh,即, (35) 当v=vr时,弹体残余长度的计算方法也与式(29)--式(30)基本相同,只需将其中的L0替换成Lres,h,v0替换为vh即可。 (36) 除去蘑菇头之外,弹体的残余长度可以近似表示为 (37) 在刚体侵彻阶段,残余弹体的Prig,r为 (38) 式中,mres为残余弹体质量;二次侵彻深度的计算方法与Yp>α0中的侵彻深度计算方法相同,即, (39) 1.2.4vr和vh的确定 (40) vr=F-1(YpA0) (41) 其中,F-1为F的反函数。 基于先前的工作[25],本文认为,判断弹体是否进入销蚀侵彻状态的主要依据为长杆弹头部是否形成了稳定的蘑菇头。由式(11)和式(12)可以看出,长杆弹形成稳定蘑菇头,且销蚀碎片抛射出的条件为 (42) 因此,vh的计算公式为 (43) 其中,uh为v=vh时所对应的弹体的侵彻速度。 图5卵形4340钢弹侵彻不同强度混凝土靶板模型预测深度与实验数据[2-5]比较 从图5中可以看出,与He[16]及Forrestal[15]的模型相比,本文理论模型预测的刚体侵彻深度与实验得出的结果十分吻合。 Kong等利用45#钢平头弹正撞击半无限混凝土靶的侵彻实验[9],如图7所示。从图中可以观察到弹体在侵彻过程中的3种状态。该实验中,弹击的冲击速度为510~1 855 m·s-1,ρp为7 757 kg·m-3,υ为0.3,Y0为380 MPa,Yp为665 MPa。L0为30 mm,r0为3 mm。 (a)v0=238 m·s-1 (b)v0=276 m·s-1 (c)v0=314 m·s-1 (d)v0=370 m·s-1 图745#钢弹残余弹体实验图[9] Fig.7Post-test photographs of 45# steel penetrators[9] 本模型计算中将弹体假定为球形弹,将上述参数代入式(41)和式(43)得到,vr为599 m·s-1,vh为1 503 m·s-1,这些理论计算值与实验观察结果[9]一致。当弹体以较高冲击速度侵彻混凝土靶板时,由于烧蚀和磨损效应会造成一些质量损失,这将在以后的工作中予以考虑。 弹体形成的蘑菇头半径与初始半径的比值R/r0和弹体撞击初速v0的关系为 599 m·s-1≤v0≤769 m·s-1 (44a) 769 m·s-1 (44b) (44c) 图8(b)为理论模型预测的弹体残余质量与实验结果[9]的比较。由图8(b)可知,本模型的预测结果与实验数据基本吻合。当v0>vh时,弹体残余质量随冲击速度的增加而减小,当冲击速度为1 200~1 500 m·s-1时,模型预测的弹体残余质量高于实验结果,而当冲击速度高于1 500 m·s-1时,模型预测结果相比实验结果偏低。需要注意的是,模型并没有考虑在较高的侵彻速度下,烧蚀和磨蚀效应造成的一些弹体质量损失。 (a)Diameter of residual penetrator (b)Mass of residual penetrator mass 图9给出了模型预测的总侵彻深度随冲击速度的变化关系,并与Kong等得到的实验数据[9]进行比较,图中虚线表示无相互作用模型预测的侵彻深度,实线表示与残余弹体有相互作用模型预测的侵彻深度。 图9本文模型预测的侵彻深度与实验数据[9]的比较Fig.9Comparison of our model predictions with the experimental data[9] 如果弹体未完全销蚀,销蚀碎片形成的圆管与残余弹体之间有相互作用,那么碎片圆管对总侵彻深度的影响可以忽略;如果弹体完全销蚀,销蚀碎片直接对混凝土靶板产生二次侵彻,那么就需要考虑其对总侵彻深度的贡献[25]。因此总侵彻深度可以写为 Ptot=Ppri+Psec,v0>vce (45a) Ptot=Ppri+Pdef+Prig,v0≤vce (45b) 其中,vce为弹体完全销蚀的临界速度; 对于45#钢弹侵彻半无限混凝土靶板,vce为2 380 m·s-1。 从图9可以看出,本文模型很好地预测了弹体在变形侵彻阶段和销蚀侵彻阶段的侵彻深度,但对刚体侵彻阶段的侵彻深度预测过高,这是因为目前的模型是针对球头弹建立的,而实验中使用的是平头弹,与球头弹相比,平头弹所受阻力更大,因而会导致侵彻深度更小。当冲击速度高于2 500 m·s-1时,利用式(32)与式(45)计算得出的侵彻深度几乎相同,因为此时弹体近乎完全销蚀。由此可以发现,式(32)和式(45)分别代表弹体能以销蚀状态侵彻混凝土靶体的总侵彻深度的上、下限。此外,本模型预测的3种侵彻模式与实验观察结果基本一致。 表1本模型计算中的各参数值 Tab.1Thevaluesofvariousparametersusedinourmodelcalculation f'c/MPaρt/(kg·m-3)a0/(108 Pa)a1/(105 kg·m-2s-1)a2/(kg·m-3)50.0[9]2 2003.123.442 45539.0[7]2 4092.915.12 636 44.1[7]2 5353.204.83267751.9[7]2 5173.306.212 63765.6[7]2 4373.767.022 64937.4[7]2 2402.953.862 575vr/(m·s-1)vh/(m·s-1)vc/(m·s-1)vce/(m·s-1)5991 5037692 3804901 4166292 1004261 3855442 0803601 3714572 0702901 3993552 0704101 0815102 430 图10本文模型预测侵彻深度与锥头铜弹侵彻不同强度混凝土实验结果[7]的比较 图11给出了本文理论模型预测的侵彻深度与球形铜(OFHC)弹正撞击37.4 MPa混凝土靶实验结果[6]的比较。 图11本文模型预测侵彻深度与OFHC铜弹侵彻半无限混凝土靶实验数据[6]的比较Fig.11Comparison between our model predictions and the test data [6] for the penetration of concrete targets struck normally by copper (OFHC) penetrators 值得注意的是,在Gold等的实验中[6],相同的弹体以较高撞击初速侵彻混凝土靶板后还有弹体残余,而在撞击初速度较低时,弹体完全销蚀,这也许是其实验数据分散的原因。虽然如此,总体上讲,模型预测的侵彻深度与实验数据大致吻合。从图11中可以明显看出,本文模型预测结果与锥形铜弹侵彻混凝土靶板的实验数据吻合较好。 图12为本文理论模型预测的侵彻深度随时间变化的曲线与Gold[6]实验数据的对比,弹体冲击速度为1 836 m·s-1,图中虚线为A-T模型预测的侵彻深度时程曲线。从图中可以看出:本文模型预测结果优于A-T模型的预测结果,与实验数据吻合较好。 图12本文模型预测的侵彻深度时程曲线与实验数据[6]的比较Fig.12Comparison of the model predictions with the experimentally obtained penetration-time history[6] 本文对长杆弹侵彻半无限混凝土靶体问题进行了理论分析, 在已有的长杆弹侵彻金属靶理论模型的基础上,在统一框架内建立了混凝土侵彻的理论模型。模型中根据弹体动态强度Yp和靶板静阻力a0的相对大小,将混凝土侵彻问题分为Yp≤a0和Yp>a0两类情况分别进行了讨论: 1)Yp≤a0:当长杆弹撞击初速度v0小于界面失效速度vid时,长杆弹不能侵彻混凝土靶板;当v0大于vid时,弹体只能以销蚀状态侵彻靶板。 2)Yp>a0:通过刚体速度vr和流体动力学速度vh将弹体侵彻过程分为3个阶段。当v0小于vr时,长杆弹以刚体状态侵彻靶板;当v0介于vr和vh之间时,弹体以变形非销蚀状态侵彻靶板;当v0大于vh时,弹体以销蚀状态侵彻靶板。此外,理论确定了这两个临界速度,并给出了相应的计算公式。 3)当弹体完全消失时需要考虑弹体销蚀碎片对混凝土靶二次侵彻的影响。 4)模型预测结果与实验得到的侵彻深度、侵彻模式、残余质量和时程曲线等数据吻合得较好,验证了本文理论模型的准确性。
1.2 Yp>a0





2 与实验结果的比较与讨论


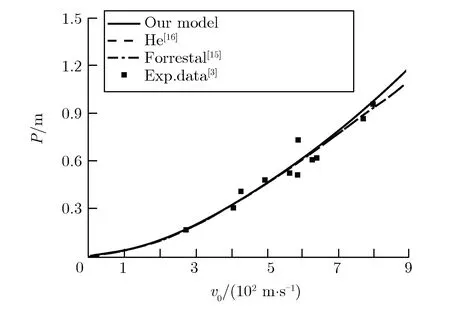


Fig.5Comparisonofourmodelpredictionswithtestdataforthepenetrationofconcretetargetsimpactedbyrigidogival-nosed4340steelprojectiles













Fig.10Comparisonofourmodelpredictionswiththetestdata[7]forthepenetrationofcopperpenetratorsintoconcretetargetswithunconfinedstrength

3 结论
