系统电磁脉冲模拟中的发射电子参数计算

陈剑楠，陶应龙，陈再高，王 玥

(1.西北核技术研究所，西安710024；2.西安交通大学电子与信息工程学院，西安710049)

系统电磁脉冲(system-generated electromagnetic pulse, SGEMP)是X射线或γ射线作用于腔体并在腔体内外引发的电磁脉冲，是核电磁脉冲的重点研究内容之一[1]。由于高空环境下空气稀薄，X射线与γ射线的作用范围和破坏影响相当大，所以需要解决卫星、弹道导弹等空间飞行器在强射线辐射环境中的生存问题。在SGEMP模拟中，电子发射状态的确定对SGEMP计算结果起决定性作用。模拟中，为了简化计算，电子状态参数通常取近似值[2-4]。本文利用蒙特卡罗(Monte Carlo, MC)程序MCNP模拟了X射线辐照圆柱腔体的光电子发射过程，计算了SGEMP模拟中需要的发射电子能谱、角分布、光电产额及不同黑体温度X射线的能谱参数。在计算电子能谱中表征射线能量的能谱参数E1时，发现了用射线黑体温度T代替E1的近似取值方法，并利用全电磁粒子模拟(particle in cell, PIC)程序对MC模拟和近似取值两种能谱取值方式下的SGEMP计算结果，进行了对比分析。

1 计算模型

计算模型如图1所示。一束平行X射线沿轴向均匀照射在圆柱腔体的端面。圆柱腔体外径D为21 cm，柱长L为21 cm，材料为铝。X射线能谱是温度为T的黑体辐射谱。X射线时间谱为

N(t)=N0sin2[πt/(2τ)]

(1)

其中，τ为半高宽;N0为积分常量。电子发射面取为受照的端面。因为发射面为平面，所以可认为整个端面是均匀发射，各点发射状态相同。

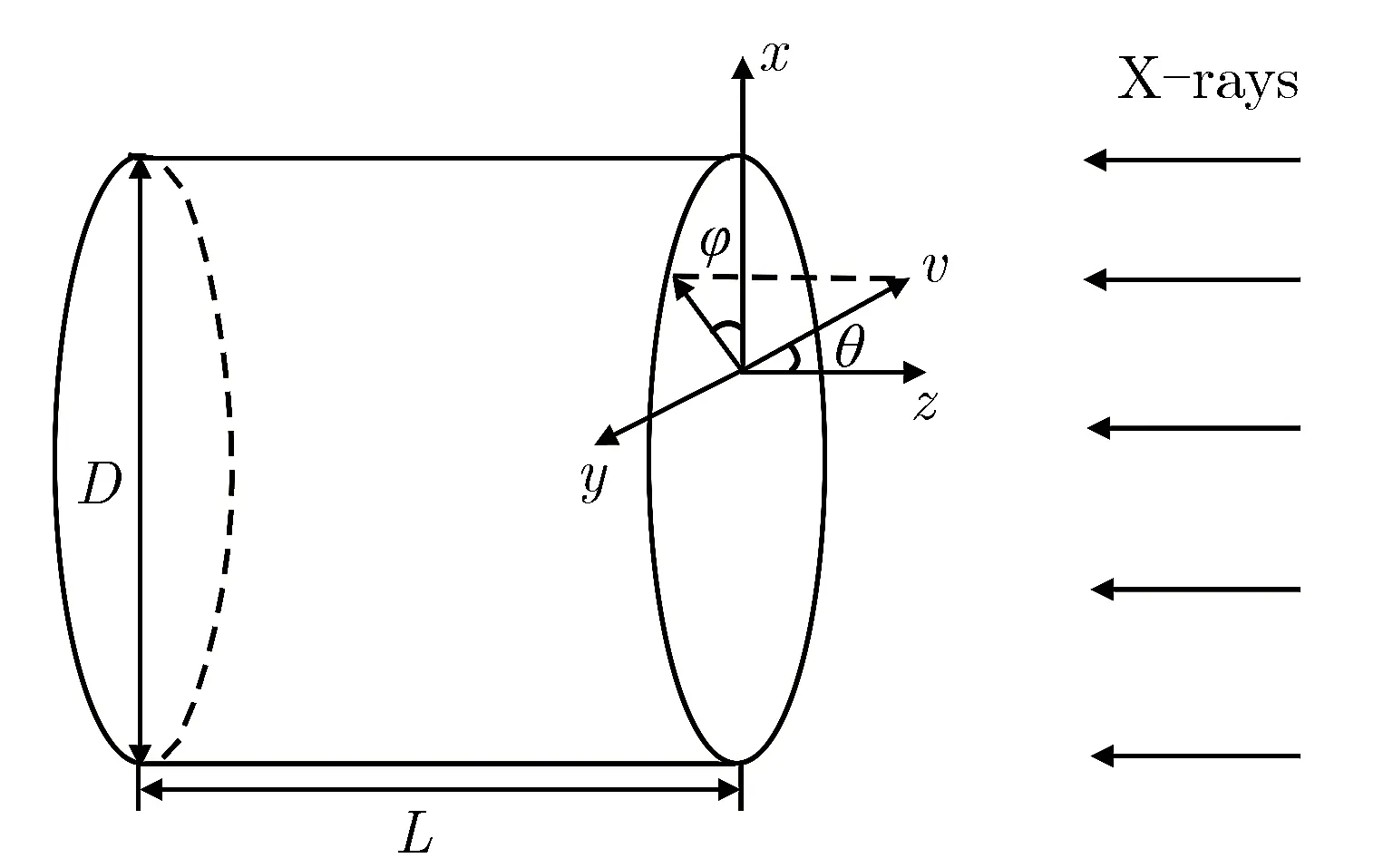
图1计算模型Fig.1Computational model

X射线入射腔体，与腔体介质发生相互作用，主要是光电效应，在端面的内、外壁面分别向腔外和腔内发射光电子，从而在系统周围和内部激励电磁脉冲，产生的电磁场为TM模。

2 电子发射参数计算分析

利用MCNP程序，计算了不同黑体温度的X射线照射圆柱腔体时的电子发射参数，包括光电产额、出射电子角分布和出射电子能谱，可以为SGEMP的计算提供较为准确的电子发射信息。

2.1 光电产额

为了与文献[5]的结果进行比对，本文给出了能量为1 cal(1 cal=4.187 J)的不同黑体温度的X射线辐射平板铝靶产生的背向散射光电子数N，如表1所列。可见，本文计算结果与文献[5]中的值符合较好；并且，随着X射线黑体温度T的增大，光电子数随之减小。这主要是因为： 1)在X射线注量不变的条件下，X射线能量越高，参与反应的光子数目越少，因此产生的光电子数目降低； 2)低能光子与Al主要发生光电效应，Al的光电效应作用截面σ随光子能量E的变化，如图2所示。可见，光电效应作用截面随着X射线能量增大而不断减小，即发生光电效应的概率不断降低。因此，在二者的共同作用下，光电数随X射线能量增大而减小。

表1不同黑体温度的X射线辐照平板铝靶产生的背向散射光电子数

Tab.1BackscatteredphotoelectronnumberofAlforvariousblackbodytemperatures

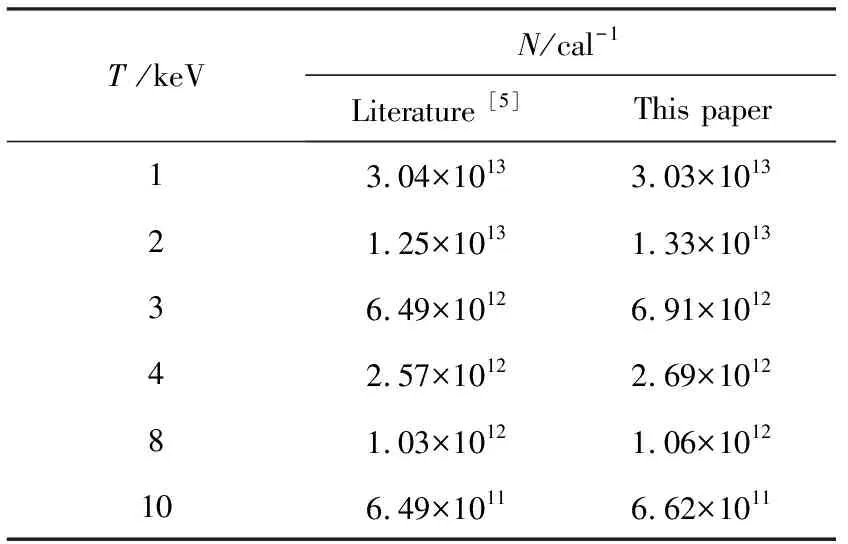
T /keVN/cal-1Literature [5]This paper 13.04×10133.03×101321.25×10131.33×101336.49×10126.91×101242.57×10122.69×101281.03×10121.06×1012106.49×10116.62×1011

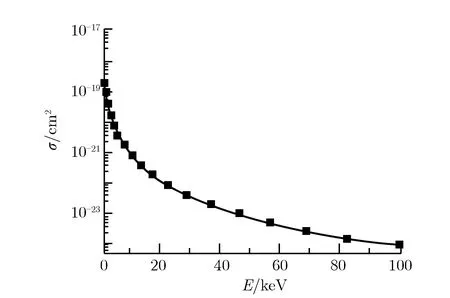
图2Al的光电效应作用截面随X射线能量的变化Fig.2Photoelectric cross section of Al vs. energy of X-rays

定义光电产额Y为单位能量(1 J)的光子与材料相互作用产生的光电子数。表2给出了不同黑体温度的X射线端面入射本模型得到的前向散射光电产额YFW和背向散射光电产额YBW。光电产额随X射线能量的变化情况，如图3所示。可见，背向散射光电产额随射线能量增大而不断减小，这与表1结果是一致的。前向散射光电产额随射线能量增大呈现先增大后减小的趋势，这是由于射线穿透腔体的能力随着射线能量的增大而增大，即射线能量增大时会存在更多与腔体内壁相互作用的光子，而光电效应截面及光子数目随射线能量的增大而减小，在三者的竞争关系下，前向散射光电产额随射线能量先增大后减小。在模拟中发现，当射线能量低于2 keV时，难以在腔内形成电子出射，所以内电磁脉冲更多是对应于高能射线作用时的结果。

表2端面入射的背向及前向散射光电产额

Tab.2Backwardandforwardphotoelectronyieldsforhead-onincidence

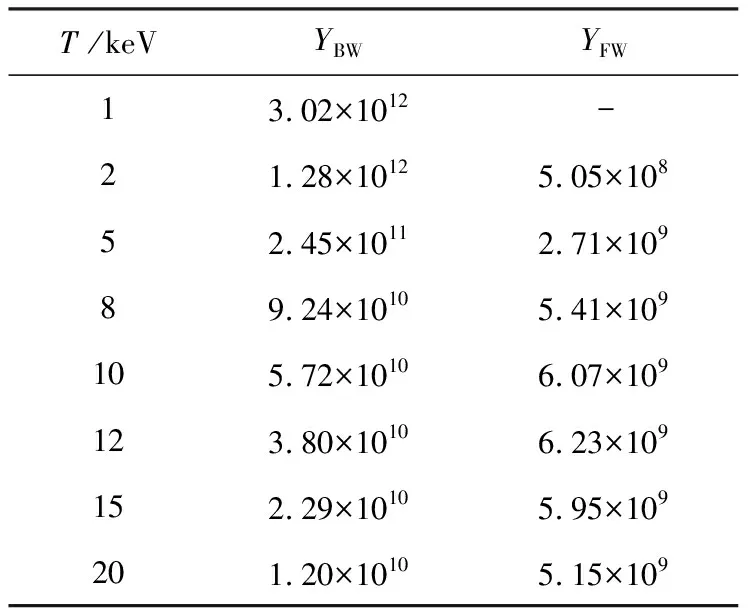
T /keVYBWYFW 13.02×1012-21.28×10125.05×10852.45×10112.71×10989.24×10105.41×109105.72×10106.07×109123.80×10106.23×109152.29×10105.95×109201.20×10105.15×109

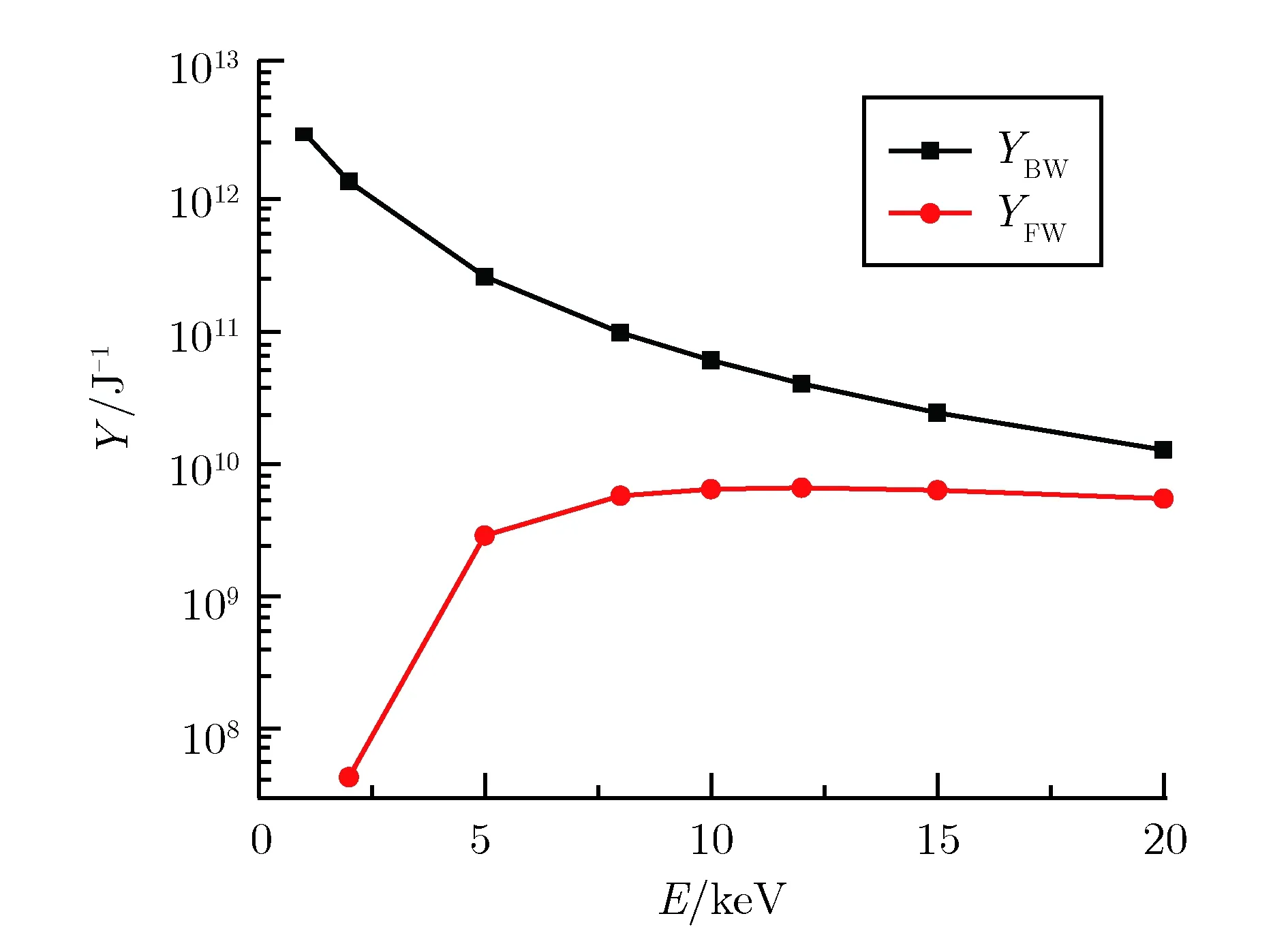
图3端面入射的背向及前向散射光电产额随X射线能量的变化Fig.3Backward and forward photoelectron yields for head-on incidence vs. energy of X-rays

2.2 角分布

发射电子的角分布包括方位角φ的角分布和偏转角θ的角分布。在本文的计算模型中，发射电子的概率密度在φ方向为均匀分布，在θ方向上与cosθ成正比[5-6]。

图4给出了X射线垂直入射本文模型时，前向散射电子和背向散射电子在θ方向上的角分布情况。可见，发射电子的概率密度正比于cosθ，与理论规律吻合较好。计算还发现，该θ方向的角分布规律在能量低于100 keV的X射线作用下具有较好的普适性，即不仅在射线垂直入射时，而且在不同入射角度下，背向散射的电子概率密度均与cosθ成正比，前向散射电子的概率密度与cosθ的绝对值成正比。

对比图4(a)和图4(b)可以看出，前向散射电子角分布曲线存在波动。这是由于前向散射电子数目较少，低能射线作用时，其电子数目比背向散射电子数目低3～4个量级，所以角分布在部分统计粒子数目较少的角度区间内存在统计误差，但是整体上与背向散射电子具有相同的角分布规律。

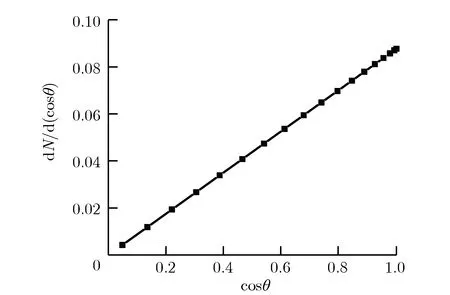
(a)Backward θ spectrum

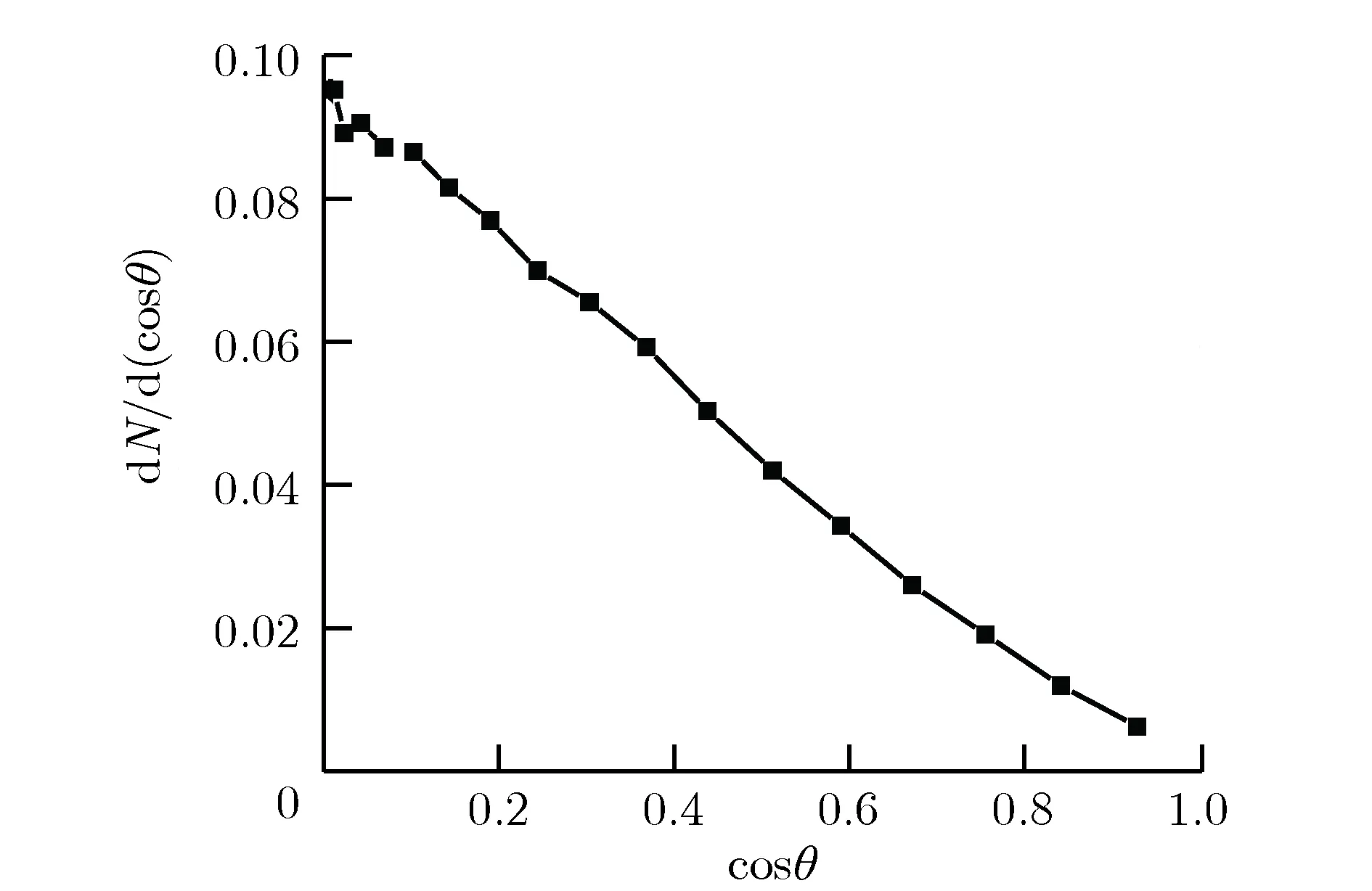
(b)Forward θ spectrum

2.3 能谱分布

利用MCNP计算得到几种黑体谱X射线产生的电子能谱，如图5所示。

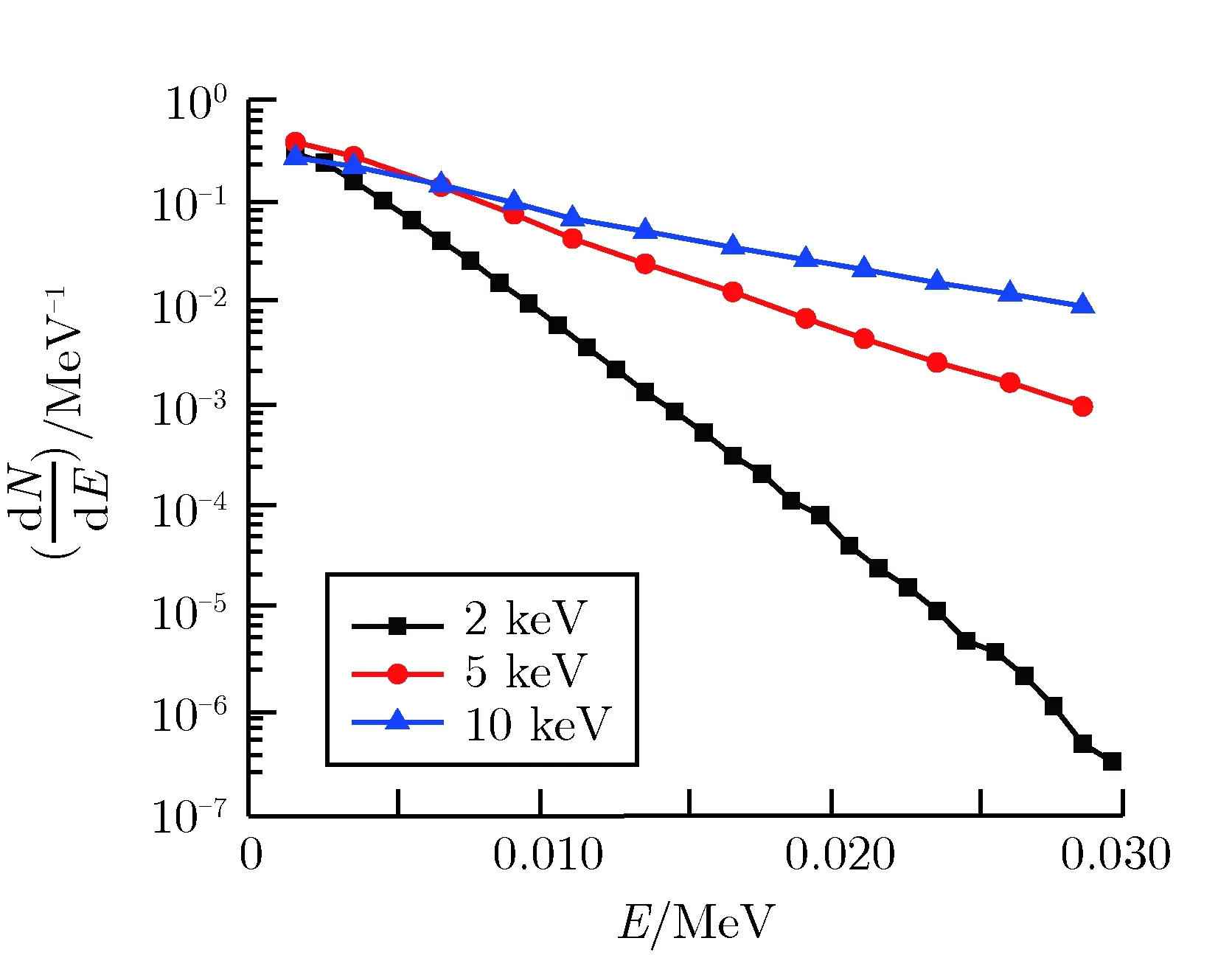
图5几种黑体谱X射线产生的电子能谱Fig.5Backscattered electron spectra for several blackbody spectrum X-rays

对图5中曲线进行拟合发现，所有黑体温度下，背向散射电子能谱均近似服从指数分布形式[5]，即

(2)

其中，E1为表征射线能量的一个参数，其值为图5中直线斜率的负倒数。通过对更多复杂模型的背向散射电子能谱进行计算，发现该指数分布规律普遍适用。本文模型中不同黑体温度X射线对应的E1，如表3所列。

表3不同黑体温度下的能谱参数E1

Tab.3ParameterE1forseveralblackbodytemperatures

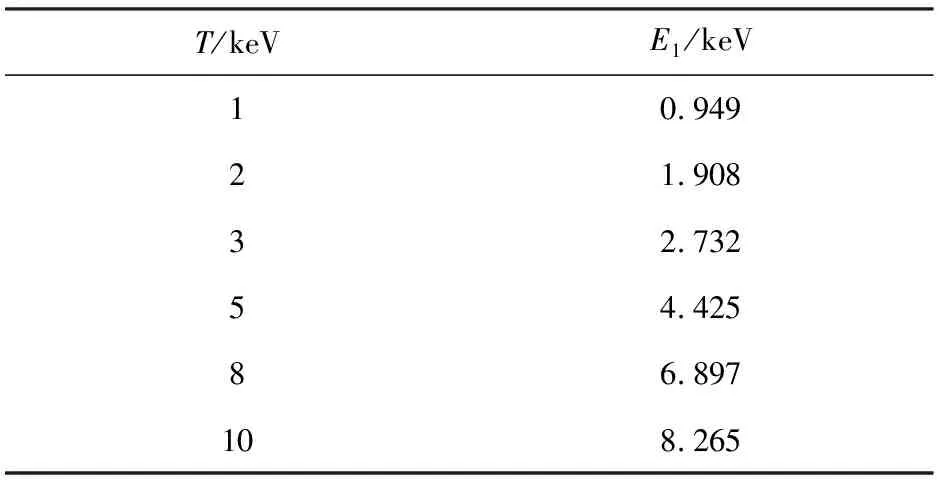
T/keVE1/keV10.94921.90832.73254.42586.897108.265

可见，在低能时，E1与X射线黑体温度T相近。因此，在文献[2-4]的SGEMP模拟中曾采用近似取值的方式简化计算，即对于特定的黑体谱射线，直接将黑体温度T作为能谱参数E1，则背向散射电子能谱经验公式为

(3)

近似取值具有一定的局限性。低能射线时，参数E1与黑体温度T偏差较小，可以直接替代；而随着黑体温度的升高，参数E1的数值会明显小于黑体温度T，二者的差值随射线黑体温度增大而增大。尽管不同计算模型下E1的数值会稍有偏差，但上述E1与T间差异的变化规律不变。下面比较能谱参数的两种取值方法对SGEMP参数的影响。

3 两种电子能谱取值方法的比较

利用MC模拟和近似取值这两种电子能谱取值方法，模拟相同条件下的SGEMP电磁场波形，对比分析电子能谱近似取值方法带来的偏差。SGEMP模拟选用3维全电磁粒子模拟PIC 程序UNIPIC[7-9]，该软件采用粒子共形的电子发射技术及电磁场共形推进算法[10-11]。

以黑体温度10 keV的X射线辐照Al圆柱腔为算例。X射线能注量Φ取4 J·m-2和400 J·m-2两种条件，其中，低能注量条件下，无空间电荷限制；高能注量条件下，存在空间电荷限制。X射线的时间谱为正弦平方脉冲，半高宽τ为25 ns。出射电子的θ方向角分布为余弦分布，φ方向角分布为均匀分布。由于可忽略光电效应的反应时间，所以发射电子的时间谱近似取X射线时间谱。

发射面上的轴向电场主要由发射面附近的电荷激励产生，圆柱侧壁磁场主要由发射电流感应产生。本文分别计算了两种X射线注量条件下，圆柱腔的发射面中心点轴向电场强度Ez和圆柱侧壁横向磁场强度Hy，如图6和图7所示。可以看出在400 J·m-2的较高注量下，由于出现了空间电荷限制，电磁场随注量的增速减弱，虽然图6与图7 中整体波形相差不大，但是不同能谱取值方式下，电磁场峰值大小关系发生了变化。两种电子能谱取值方法下计算得到的电场强度峰值Ez，peak和磁场强度峰值Hy，peak的比较，分别如表4和表5所列。以表中MC模拟结果作为参考，可以计算得到Φ为4 J·m-2时，近似取值方法得到的发射面中心电场强度峰值与参考值的偏差为-3.87%，发射面侧壁横向磁场强度峰值与参考值的偏差为0.87%；Φ为400 J·m-2时，电场强度峰值与参考值的偏差为-0.79%，磁场强度峰值与参考值的偏差为5.37%。

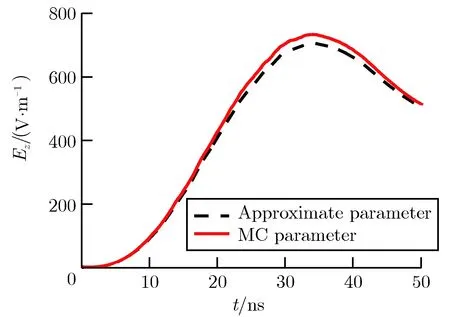
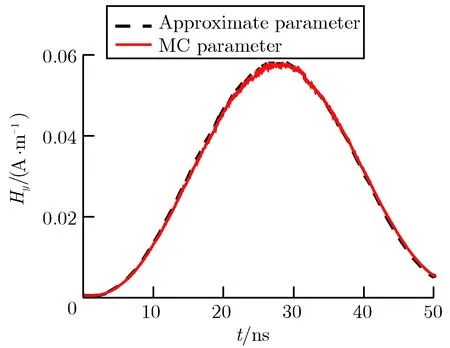
(a)Waveform ofEzat center point of emitter surface (b)Waveform ofHyat side point of emitter surface

图6Φ=4J·m-2时，两种电子能谱取值方法下的电磁场波形比较
Fig.6ComparisonofelectromagneticwaveformsofthetwoelectronspectrummethodsforΦ=4J·m-2

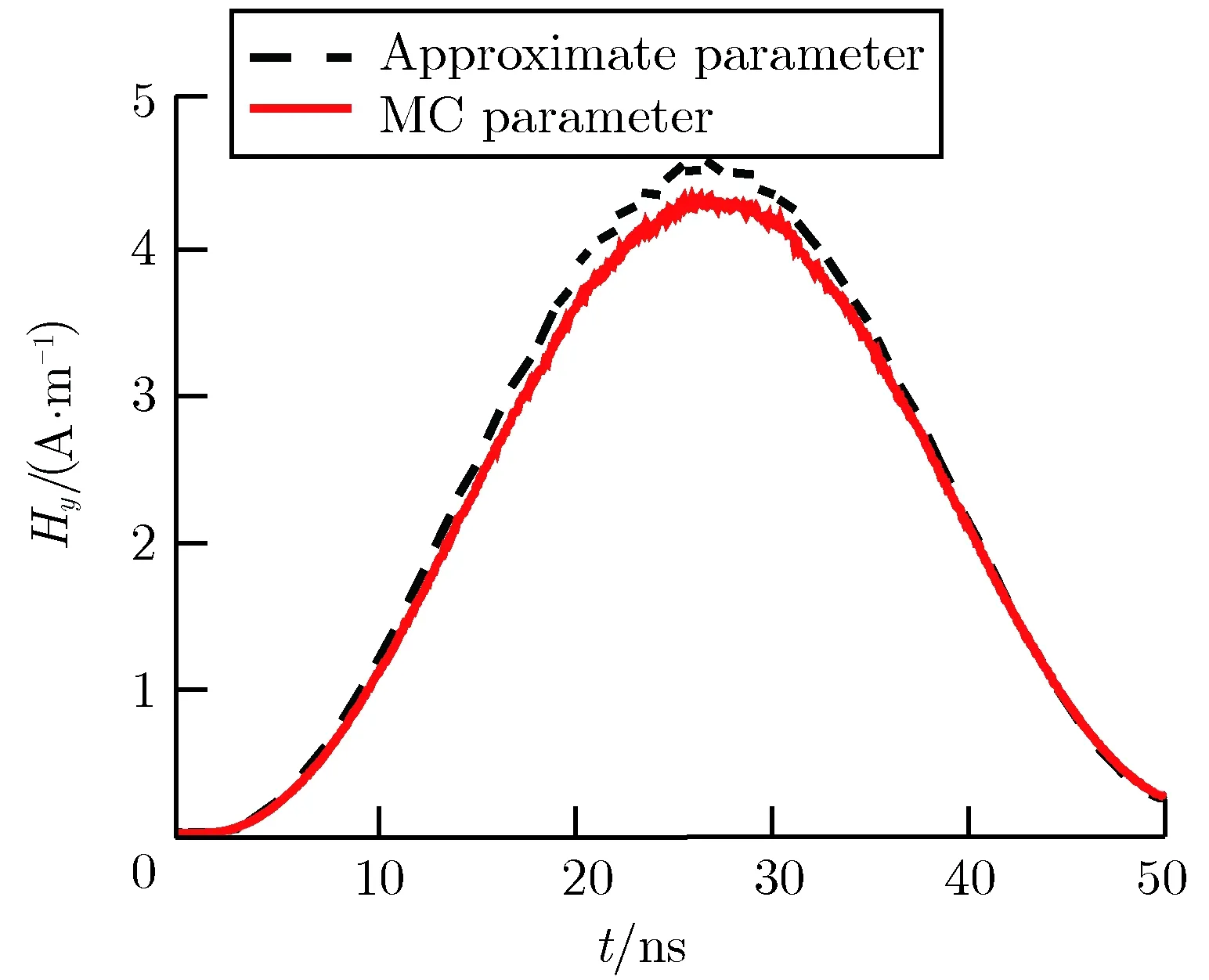
(a)Waveform ofEzat center point of emitter surface (b)Waveform ofHyat side point of emitter surface

图7Φ=400J·m-2时，两种电子能谱取值方法下的电磁场波形比较
Fig.7ComparisonofelectromagneticwaveformsofthetwoelectronspectrummethodsforΦ=400J·m-2

表4Φ=4J·m-2时，两种电子能谱取值方法计算的峰值参数对比

Tab.4ElectromagneticfieldpeakvaluesofthetwoelectronspectrummethodsforΦ=4J·m-2

MethodEz,peak/(V·m-1)Hy,peak /(10-2 A·m-1)Approximate method703.15.77MC method731.45.72

表5Φ=400J·m-2时，两种电子能谱取值方法计算的峰值参数对比

Tab.5ElectromagneticfieldpeakvaluesofthetwoelectronspectrummethodsforΦ=400J·m-2

MethodEz,peak/(kV·m-1)Hy,peak /(A·m-1)Approximate method61.214.566MC method61.704.333

由式(2)和式(3)可知，能谱参数数值越大，则对应的电子平均能量越大，高能电子数目越多。所以在相同的电子发射率下，取黑体温度T作为能谱参数将会使对应的电子能量整体增大。当电子更快离开发射面时，发射面附近的电子数目较少，其电场强度较小；而相应的发射电流密度较大，其磁场强度较大。同时，高能注量下的空间电荷限制会使得电子返回发射面，减弱电子发射能力，并使电磁场产生相应的改变。

在低能注量(Φ=4 J·m-2)的线性区域内，电子受发射面正电荷的静电作用可以忽略。此时，虽然两种取值方法存在能谱偏差，但是实际电子发射速率相差不大，故两种取值方法计算得到的发射电场强度和磁场强度偏差较小；而电场主要由电子静电作用产生，电场强度值与距离的平方成反比，速度偏差带来的影响会因距离的平方被放大。在高能注量(Φ=400 J·m-2)的非线性区域内，会出现空间电荷限制。此时大量电子回到发射面，使得不同能谱参数下的发射面电荷密度相差不大，电场强度值差别较小；而由于高能电子存在打破空间电荷限制的作用，实际发射电流主要由这些高能电子组成，其受能谱参数的影响较大，所以高能注量下反而出现电场强度值偏差减小，磁场强度值偏差增大的情况。

通过上述模拟对比发现，对黑体能量低于10 keV的X射线，由于能谱参数E1与黑体温度T的数值差别相对较小，近似取值方法所引起的SGEMP场值偏差不大。当射线能量进一步增大时，E1与T的差别增大，若仍采用近似取值方法，则带来的场值偏差会随之增大。

4 结论

利用MC方法及MCNP程序模拟并总结了光电产额、角度谱以及能谱等发射电子参数的变化规律，可为SGEMP的 PIC模拟提供准确可信的电子发射状态。针对近似取值方法和MC方法这两种电子能谱取值方式，通过PIC对不同能注量下的SGEMP进行了模拟，得到了出射电子能谱。结果表明，能谱近似取值带来的电子速率的变化，会引起SGEMP模拟计算中电磁场峰值的偏差，故为了得到准确真实的SGEMP结果，在较高能X射线作用时，电子能谱参数需通过MC计算得到。