基于激光位移传感器的倾角误差分析
2019-01-07孙兴伟赵文涛朱新华
孙兴伟,赵文涛,朱新华
(沈阳工业大学 机械工程学院,辽宁 沈阳 110870)
0 前言
随着我国航空航天、船舶舰艇、交通运输等行业的迅猛发展,对产品的精度要求也越来越高,因此精密检测技术也显得愈发重要。与传统的接触式测量相比,激光三角法因其非接触的测量特性,所以可以对表面易划伤工件进行测量,并且具有测试速度更快、测量范围大、无需二次装夹等特点,被广泛应用在工业生产和检测等领域[1-3]。但是,激光位移传感器的测量精度受其系统自身的非线性误差、被测物体表面的粗糙度、被测物体表面的颜色以及被测物体表面的倾斜角等因素的影响[4-6],导致被测物体的精度不能准确测得。因此,研究测量精度的影响因素变得尤为重要,本文对误差影响因素中影响最大的——测点物面倾斜对测量精度的影响做了分析与研究。
1 激光三角法的测量原理
典型的直射式激光三角法测量原理图如图1所示,其光路主要由激光发射装置、汇聚透镜、接收透镜、线阵COMS和后续信号处理设备五部分组成等。激光三角法的测量原理:激光源发射的激光束经过汇聚透镜后照射到被测物体的表面上,接收透镜接收由被测物体表面所反射和散射的激光束,然后在线阵COMS感光元件上成像,从而把被测物体表面的光信号转化为电信号,再经后续电路处理就可以识别出被测物体的位移变化量。测量过程中,激光位移传感器的轴线,接收透镜的光轴以及线阵CMOS平面,三者位于同一个平面内。当被测物体表面发生位移时,散射光线在线阵COMS感光元件上成像点的位置也发生变化,如果能够准确测出像点在线阵CMOS上的变化量,那么通过激光三角法的测量原理,就可以进一步计算出被测工件的移动距离。
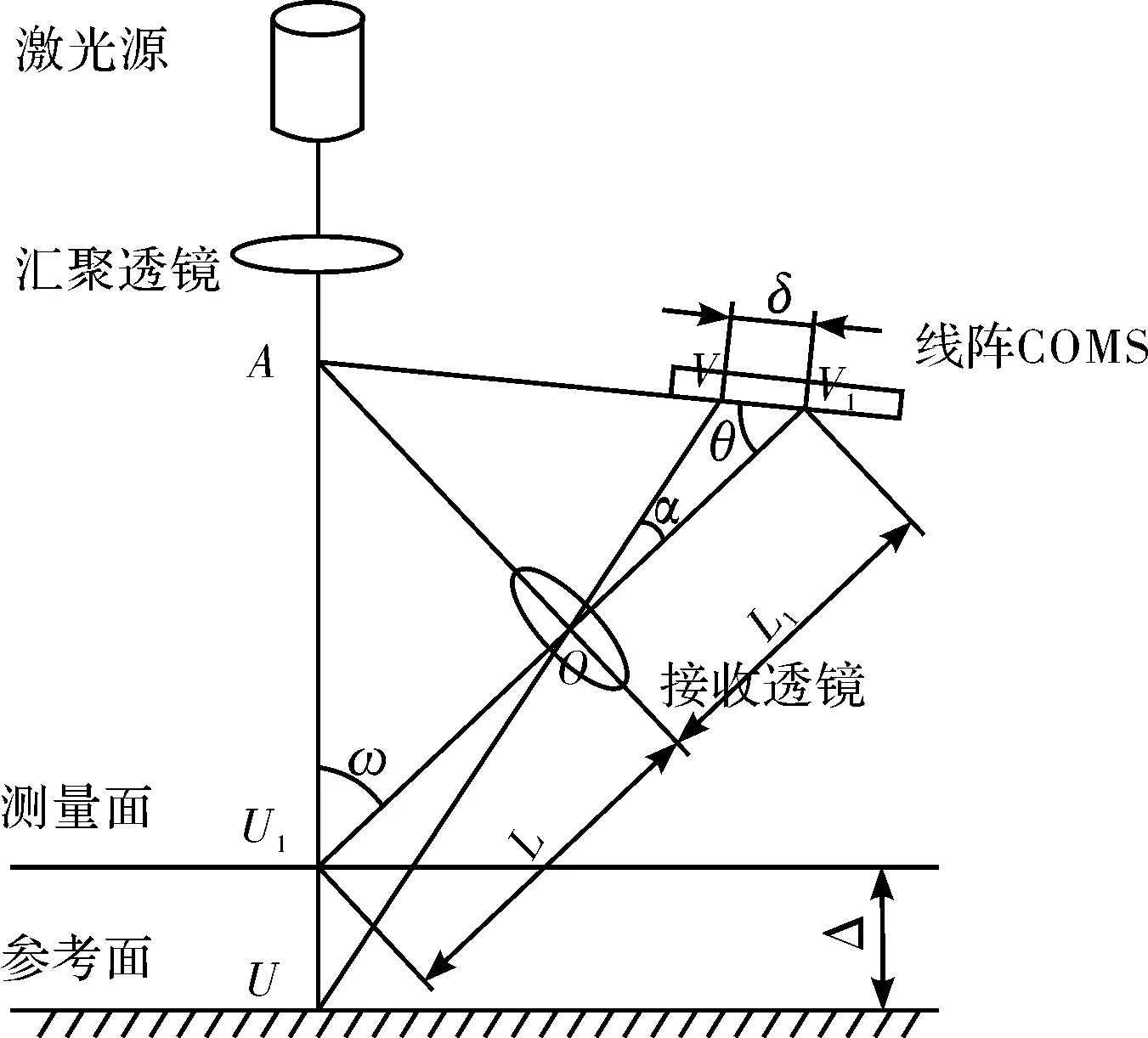
图1 直射式激光三角法测量原理图
假设当激光源发射的激光束照射到参考平面上的位置U时,散射光束经接收透镜接收后在线阵COMS上的成像位置点为V点;当被测表面发生位移Δ后(由位置U移动到位置U1),在线阵CMOS上的光斑像点发生了位移δ(由位置V变化到位置V1),根据正弦定理可得:
在ΔU1OU中,
(1)
整理得
(2)
在ΔV1OV中,
(3)
整理得
(4)
合并可得
(5)
式中,α为两条反射光束的夹角;ω为激光束与接收透镜轴线的夹角;θ为线阵COMS光敏面与接收透镜轴线的夹角;L为接收透镜的物距,即测点U1到接收透镜中心O点的距离;L1为接收透镜的像距,即接收透镜中心O到线阵CMOS上V1的距离。
2 倾角误差补偿模型的建立
2.1 倾角误差产生的原因分析
由激光三角法的测量原理可知,测量过程中激光源发射的激光束与被测物体表面的法线方向在理论上是一致的,但是在实际测量时,激光位移传感器发出的光束总是和被测物体表面处的法线方向存在一定的夹角,这个夹角称之为倾斜角,用β表示。被测物面倾斜改变了散射光束相对于接收透镜的空间位置,相应的被测点在线阵CMOS上的成像点位置也发生了变化,从而导致实际测量的结果与激光三角法测量原理中理论公式计算的结果存在一定的偏差。这就是物面倾斜时测量误差产生的主要原因。
2.2 线阵CMOS上汇聚光斑的光能质心位置的确定
由倾角误差产生的原因可知,当被测物面倾斜时,检测到的线阵CMOS光敏面上的成像光斑点的光能质心位置相对其几何中心发生了一定的偏移,因此光能质心不再是成像光斑的几何中心。为了定量的分析由于被测物面倾斜造成的误差的变化规律,需要推导出在线阵CMOS上的成像光斑的光能质心位置与被测物面倾斜角之间的关系。
首先,假设被测物面为理想的漫反射面,根据郎伯定律可知,散射光场的光强分布可以表示为[7]
I(φ)=I0cosφ
(6)
式中,φ为散射光束与物面法线的夹角;I(φ)为φ方向上单位立体角内的散射光功率值;I0为法线方向的I值。
2.2.1 接收透镜上光能质心线角位置的确定
图2给出了接收透镜上接收面元的几何示意图,其中r=UO,即被测物光点U到接收透镜中心O的直线距离,dS为接收透镜上与接收面垂直的条状面元,dΩ为该条状面元所对应的物光点所张的立体角。由于接收透镜的半径R很小,所以近似地认为该面元上的散射光处处相同。因此,在单位时间内dS接收的光能为
dE=Icos(γ0-γ)dΩ
(7)
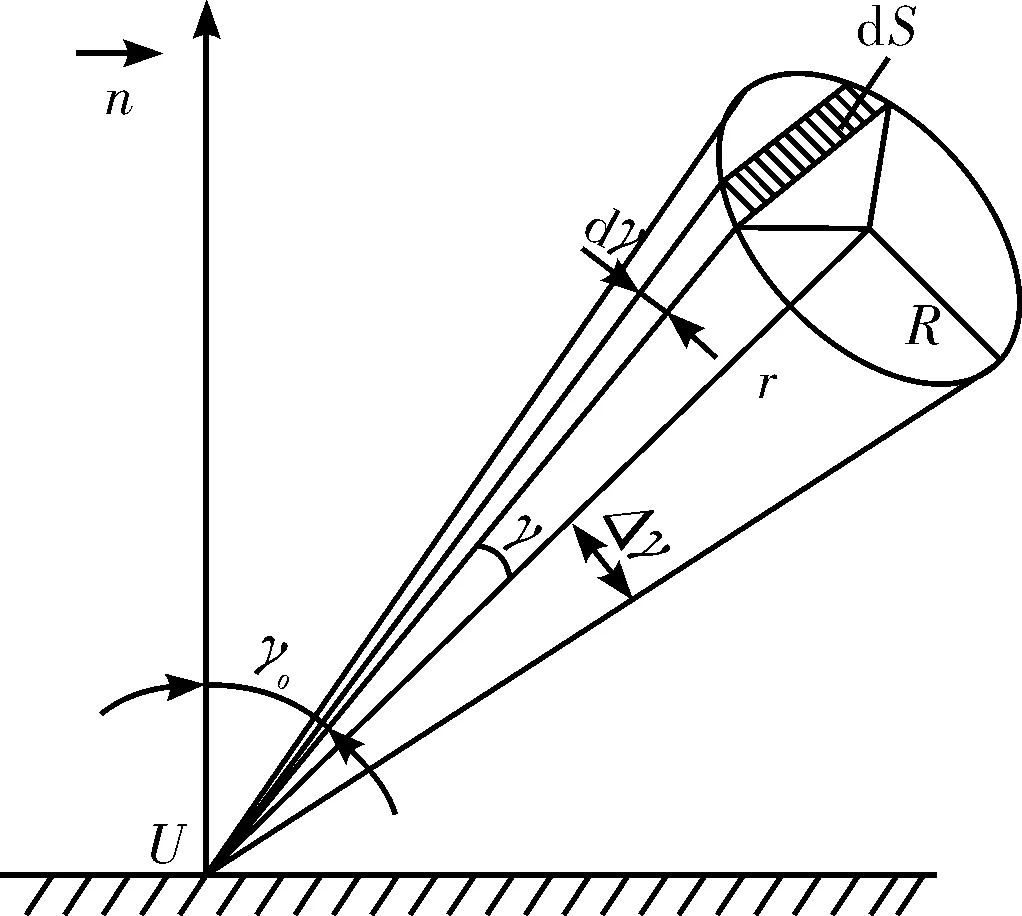
图2 接收面元几何示意图
根据接收面元几何示意图可知:
(8)
(9)
由于R≤r,将式(8)、(9)带入(7)整理得
(10)
本文中当γ顺时针转动时为正。假设当γ=γ′时,接收透镜在垂直接收面处被分成两个光能接收量相等的部分,此时称γ′为接收透镜上光能质心线的角位置。
(11)
整理后得出接收透镜上光能质心线的角位置γ′为
(12)
2.2.2 线阵CMOS上汇聚光斑的光能质心位置的确定
图3给出了线阵CMOS上汇聚光斑的光能质心示意图,反射光线MB经接收透镜折射后入射到线阵CMOS上的C点。M的像点为M2,物距a与像距b满足
(13)
根据几何关系可推得
(14)
(15)
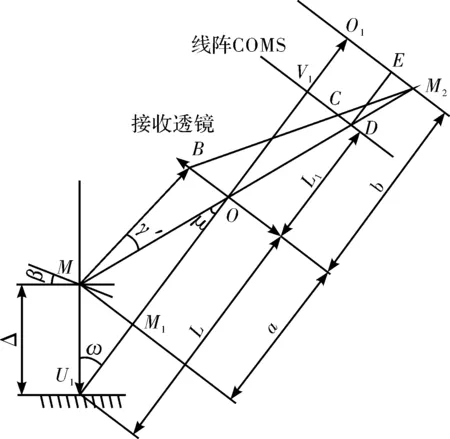
图3 汇聚光斑的光能质心示意图
所以质心线在线阵CMOS上的投射点C的离轴距离为V1C,也就是V1D与CD的差,即线阵CMOS上汇聚光斑的光能质心坐标为
(16)
2.3 物面倾斜造成的测量误差的确定
根据式(12)、(16)就可以求出被测物面的倾斜误差,从而分析其变化规律。
当激光位移传感器的入射光线与被测物面的法线方向一致,即物面的倾斜角为0时,线阵CMOS上成像光斑的光能质心坐标为
(17)
式中,γ″是被测物面倾角为0时的γ′值。
所以由物面倾斜产生的线阵CMOS上光斑的光能直线移动量为
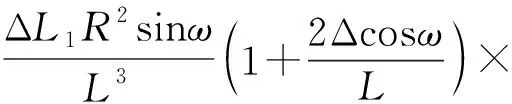
[tanω-tar(ω-β)]
(18)
由此可知Δ″与倾角误差Δ0之间的关系为
(19)
整理后得到倾角误差Δ0为
(20)
根据式(20)可知,倾角误差Δ0除了与激光位移传感器的结构参数有关外,还和被测物体表面移动距离Δ以及物面倾角β有关,并且可以发现如下规律:
(1)倾角误差的大小与激光位移传感器的结构参数有关,与R2成正比,与L2成反比,且随着ω角的增加而增大;
(2)当被测物体表面的位移Δ一定时,倾角误差随倾斜角β的增加而增大;
(3)当倾斜角β一定时,倾角误差随被测物体表面的位移Δ的增加而增大;
(4)当β为负值时,倾角误差的正负与被测物体表面位移的正负相反;当β为正值时,倾角误差的正负与被测物体表面位移的正负相同。
3 倾角误差实验分析
实验采用日本KEYENCE公司生产的IL-030型激光位移传感器进行了实际测量,其光路参数为:R=5 mm,L=60 mm,ω=30°,将实验测得的数据与经过误差补偿后的数据用MATLAB处理后得到图形如图4所示。
通过图4可以看出,激光位移传感器的测量精度在经过倾角误差补偿公式补偿后得到了明显提高。
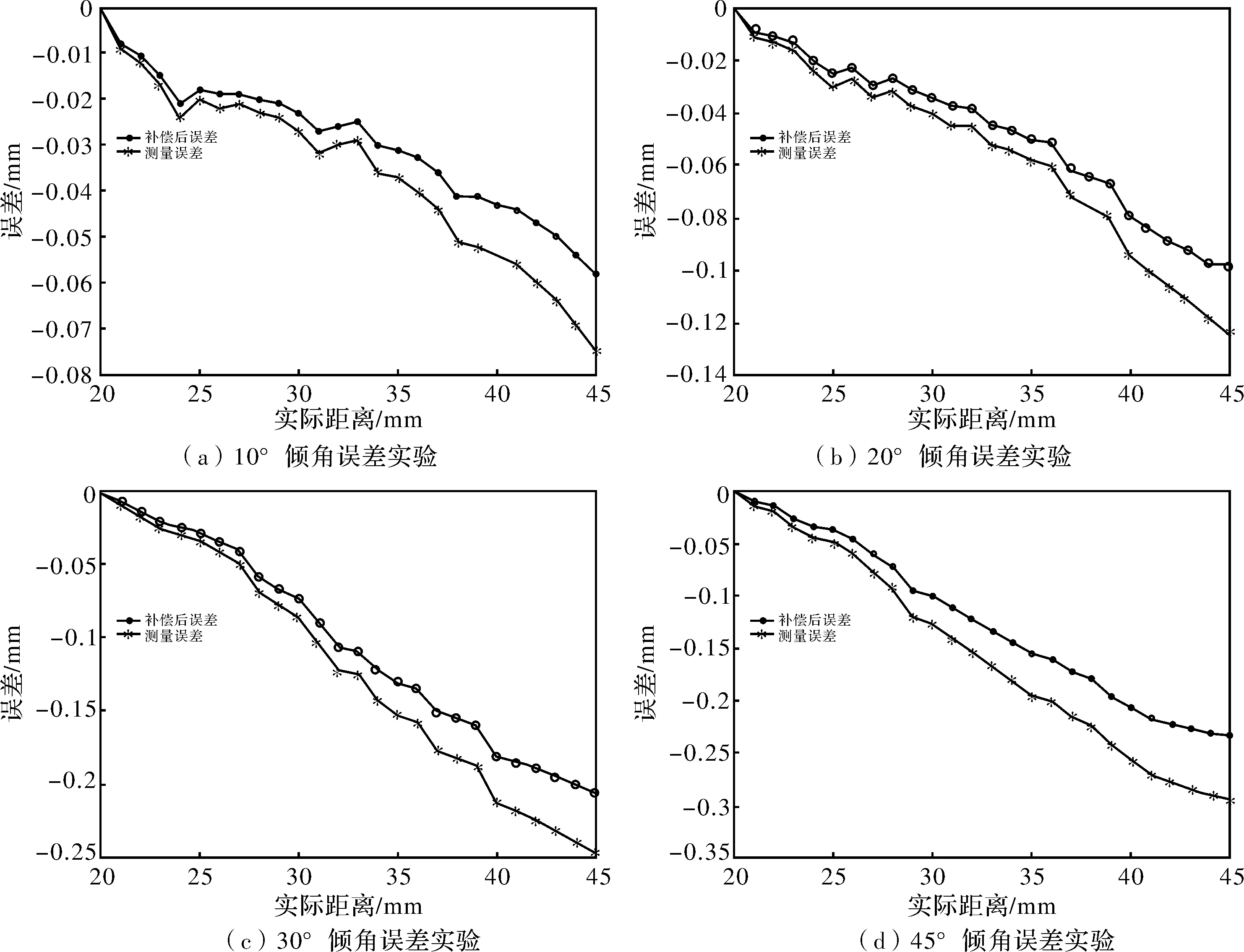
图4 倾角误差补偿实验曲线图
4 结论
在假设被测物面为理想的漫反射面的前提下,推导出了被测物面倾斜角与测量误差的几何关系。实验表明,该方法提高了被测物面的测量精度,对产品的加工和检测具有一定的指导意义。
