基于目标机动预估的空空导弹可发射区建模及仿真分析
2019-01-05丁达理董康生
王 杰,丁达理,许 明,董康生,库 硕
(1.空军工程大学 航空工程学院,陕西 西安710038;2.中国人民解放军95478部队,重庆 401329)
可发射区是衡量空空导弹战术使用性能的最重要因素。通过对当前空战态势下的导弹可发射区进行快速解算,掌握导弹的攻击特性和限制范围,在保证命中概率的前提下,拓宽导弹的可攻击边界,有利于高效地发挥空空导弹的作用和攻击机可靠攻击占位,具有重要的军事意义。
近年来,针对空空导弹可发射区问题,国内外学者从以下几个方面进行研究:①从概念角度阐述可发射区的表征思路和分析方法[1];②通过多层感知机[2]、遗传规划[3]等方式,实现对空空导弹可发射边界的预测;③双机[4]及多机[5]编队条件下空空导弹协同可发射区域;④空空导弹发射后的动态发射区[6],及随机风场[7]等实际约束条件下射后动态可发射区的规律及变化。
分析现有文献,在对导弹可发射区解算时,均使目标保持直线定常状态或给定的机动状态。现代空战的高对抗性,意味着目标机动变化十分剧烈。在对可发射区解算时,若能通过一步预估的形式对目标的机动行为做出预判,得出更符合目标状态变化实际的可发射区解算结果,将有利于攻击机提前做好攻击准备,更好地做出机动选择,从而有利于拓宽导弹的可发射边界,便于导弹作战使用性能的充分发挥。而基于目标机动预估的导弹可发射区问题至今尚无公开文献涉及。
在前人研究的基础上,本文提出基于目标机动预估的空空导弹可发射区的新概念。仿照人在回路中的决策方式,从战术层面,对目标机最大概率的机动行为进行一步预估;在此基础上,采用改进的黄金分割搜索策略实现对导弹的可发射区边界值的快速精确求解。
1 导弹可发射区问题描述
空空导弹可发射区是指以攻击机为参考中心,在满足一定攻击条件下,攻击机发射导弹且能以一定的概率命中目标的初始位置范围[4,8]。导弹的可发射区主要受导弹性能、目标运动状态和攻击机运动状态的影响。相同初始状态下,同一型导弹,随目标进入角不同,可发射区范围存在很大差异。在表现形式上,可分为水平可发射区[1]、垂直可发射区[1]和倾斜面可发射区[9]等形式,通常采用水平可发射区用于可发射区问题的描述。
当目标机进入攻击机火控雷达截获距离范围内时,导弹导引头位标器解锁,导引头偏离导弹轴线瞄准、捕获并稳定跟踪目标,最终实现导弹发射。受发射前导引头位标器所允许的动态视场角限制,存在最大离轴发射角βmax。假定目标运动规律已知,以攻击机为中心,在导弹最大离轴角允许的范围内,随目标方位角的不同,计算出导弹能够命中目标的最远距离和最近距离,即可发射区的远边界和近边界。由远边界、近边界及导引头动态视场角等约束形成的包络,即为导弹的可发射区,如图1所示。
传统意义上的可发射区,在解算时往往取决于导弹发射时的初始条件,即假定目标保持原运动状态,因而,难以适应目标逃逸机动的态势变化。为了适应目标逃逸机动的状态实际,存在不可逃逸区[1,10-11]的概念。在攻击平面内,同一目标方位角随目标机动方式的不同,可发射距离存在差异。在规定的目标最大机动过载范围内,使目标机以任意过载实施逃逸机动,可解算出由不同发射区域构成的攻击平面簇,这些攻击平面的公共交集即为导弹的不可逃逸区。不可逃逸区表征了导弹的最大攻击能力,在不可逃逸区内,理论上无论目标实施何种逃逸机动,导弹都可以以一定的概率命中目标。显然,由于需要兼顾所有可能的机动情况,不可逃逸区的范围必然较小。
2 基于目标机动预估的空空导弹可发射区问题
基于目标机动预估的可发射区是指:模仿人在回路中的决策方式,根据导弹发射时刻目标机与攻击机之间的相对态势关系,预估目标机为避免被直接瞄准而采取的机动应对策略。根据目标机动预估结果,基于导弹飞行状态、发动机工作状态、弹体质量、制导导航与控制系统等各子系统的状态,在各种约束条件下,能够以一定的概率命中目标的平面或空间区域。相较于传统意义上的可发射区和不可逃逸区,该发射区在解算方法上往往是一致的,区别在于对目标逃逸机动状态进行了一步或多步预估,以适应剧烈的空战态势变化。
由于精确预测目标的运动状态十分困难,且考虑到目标实际机动能力大小难以界定,因而,本文首先根据发射时刻、导弹与目标的相对方位信息,从战术层面,基于导弹实际战术使用性能,对目标可能的逃逸机动方式进行一步预估。
导弹实际作战使用中,当攻击平面内离轴发射角为0,即机头直接指向瞄准的情况下,导弹受导引头视场角限制的程度最低,因而具有最大的命中概率。目标机为避免攻击机达成机头直接指向瞄准的不利态势,应朝向远离攻击机机头方向实施逃逸机动,即目标沿远离攻击机机身轴线方向具有更大的概率意图。对于目标做三维机动的预估问题,是一种多步预估问题。在战术层面上,对目标做三维机动的预估难以实现,因此文中主要考虑目标做二维机动的情况;从能量角度和操控便利性来看,目标机并不会频繁地进行俯冲和拉升机动,为简化计算过程,并尽可能地保证预估目标信息的可靠性,文中假设目标仅在水平面内实施逃逸机动。
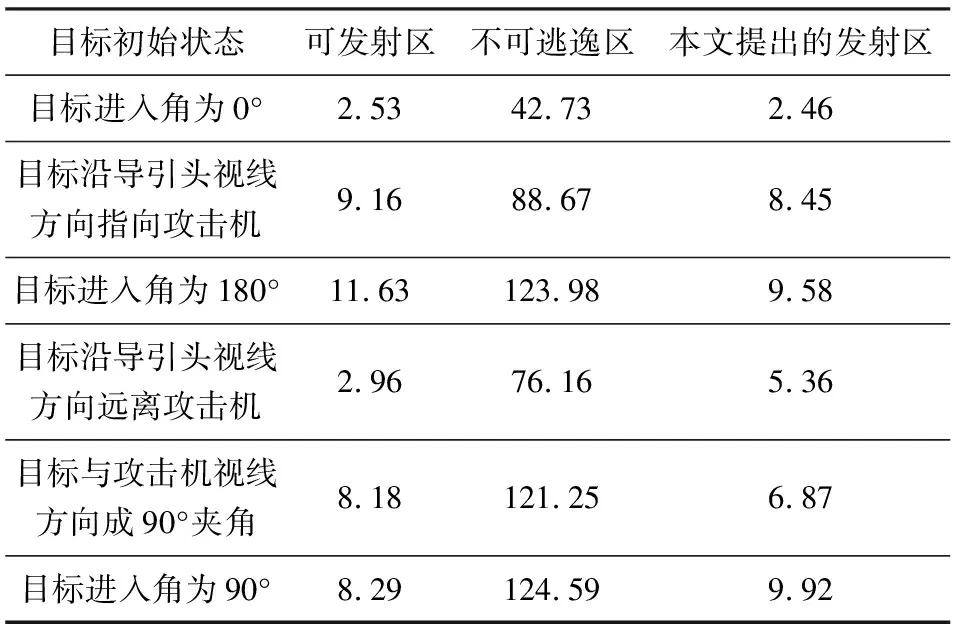
如图2所示,当目标机头瞄准本机飞行的条件下,目标进入角满足π/2<|aoff|≤π。若目标机位于本机左侧,即目标方位角0 目标方位角目标进入角目标机动意图概率目标机动预估结果0 由于目标机动实施时,其侧(法)向过载的实际大小对可发射区域的解算面积存在较大影响。且考虑到,实际空战中目标机动能力的大小不易界定,因此文中假设目标在导弹发射时刻侦测到攻击机信息,且以平台极限过载实施逃逸机动。 综上分析可知,本文提出的机动预估方式是战术层面上的。所采取的目标机动预估方式,将是否沿远离攻击机机身轴线方向实施逃逸作为概率大小评判的标准,是符合人在回路中的决策思维及导弹的战术使用特性的。虽然在表现形式上较为简单,但从战术层面上讲,预估的目标机动信息往往是可靠的。 惯性坐标系下,导弹运动学方程[12]为 (1) 式中:(xm,ym,zm)为导弹在惯性坐标系下的坐标;vm,γm,ψm为导弹的速度、航迹俯仰角和航迹偏转角。 弹道坐标系下,导弹的质点动力学方程为 (2) 式中:Fp,Fz为导弹的推力和空气阻力;mm为导弹的质量;nm,x,nm,z为导弹在偏航方向和俯仰方向的侧向控制过载。 Fp,Fz和mm的变化规律为[4] (3) (4) (5) 导弹采用文献[14]提出的比例导引律,并假设在相互垂直的2个控制平面内导引系数均为K,偏航方向和俯仰方向的2个侧向控制过载定义为 (6) 式中:β和ε为导弹和目标质心连线相对惯性坐标系水平和铅垂方向的夹角,即视线偏角和视线倾角。 导弹刚离开载机时,为保证载机安全和导弹顺利达到超音速,防止失控,存在非可控飞行时间t0。在该时间内,制导电路不产生控制指令,导弹做自由飞行;考虑导弹结构的稳定性,导弹侧向需用过载不应突破导弹最大可用过载nmax限制。故导弹实际控制过载n表示如下。 当t0≤t≤t0+tc时, 当t n=0 式中:n1为侧向需用过载,由式(6)求得;tc为导弹最大可控飞行时间。 目标运动模型与导弹运动动力学模型类似,不考虑目标推力及气动力的情况下,目标运动方程可简化为 (7) (8) 式中:(xt,yt,zt)为目标在惯性坐标系的位置;vt,ψt,γt为目标速度、航迹偏航角和航迹俯仰角;nt,y为沿目标速度方向的切向控制过载;nt,x,nt,z为目标偏航和俯仰方向的侧向控制过载。 为了准确描述导弹追踪过程中相对目标的位置变化,需要建立导弹-目标相对运动模型。设空空导弹相对于目标的位置矢量为r,在惯性坐标系下用(r,β,ε)表示为 (9) 式中:rx=xm-xt,ry=ym-yt,rz=zm-zt;r为导弹相对目标的距离。 对式(9)关于时间求导可得: (10) 导弹击中目标可定义为[4]:r≤e且t≥tyx。e为战斗部杀伤半径或导弹引信可靠作用距离;tyx为导弹引信解除保险时间。 导弹性能约束制约着发射区的范围,是仿真终止的关键。为了准确描述导弹的跟踪状态,基于导弹工作实际,对导弹性能约束分析如下。 ①导引头动态视场角限制。 导弹发射后,导弹-目标视线偏离导弹轴线的角度(发射后离轴角)突破动态视场角限制时,导引头丢失目标。即: (11) 式中:φx,max,φz,max分别为导弹发射后,导引头在偏航和俯仰方向所允许的最大动态视场角。 ②导弹最大飞行时间tmax限制。 当飞行时间大于导弹最大飞行时间时,导弹自毁。即: t≤tmax (12) ③目标影像探测距离限制。 对于红外型空空导弹,在初始制导时刻,导弹相对目标距离小于目标影像最小探测距离Rmin时,目标影像尺寸过大,调制盘寻的部分失去调制作用,不能形成探测信号,导弹失控。即: (13) 式中:δ是个很小的数。 (14) 式中:Rrs为相对距离判断值。 除此之外,导弹需要满足的约束还应包括:导引头跟踪角速度限制、高度限制、导弹最小可控速度限制、战斗部有效起爆区限制等,在此不做赘述。 为了快速有效地求解基于目标机动预估的空空导弹可发射区边界包络,需要对攻击机周围目标的位置进行搜索,即通过仿真打靶验证:当目标初始位置在某一点,且执行预估逃逸机动的情况下,导弹能否以一定概率命中目标。 在一维搜索中,黄金分割法具有不需要预先知道搜索循环次数、收敛速度快的优点,因而在描述可发射区解算问题的文献[4,15]中被广泛采用。以导弹发射载机为坐标原点建立坐标系,其基本原理如下。 首先在导弹离轴角允许的范围内,确定目标初始位置相对于载机的方向,即确定目标方位角;预估初始距离范围[a0,b0],计算黄金分割点R0=a0+0.618(b0-a0);以分割点位置为目标初始位置进行仿真,根据导弹性能约束判断导弹是否命中目标。在远边界搜索中,如命中目标,令a1=R0,b1=b0;如未命中,则令a1=a0,b1=R0;重新循环计算,直到求出满足约束|bi-ai|<δ′的边界为止。近边界搜索与远边界类似,在命中目标时,令ai=ai-1,bi=Ri-1,否则令ai=Ri-1,bi=bi-1。距离找到后,改变目标方位角或俯仰角,重新计算,直到导弹导引头可探测的角度搜索完毕为止;最后,所记录的Ri-1值即为空空导弹可发射区的边界值。 由上述分析可知,黄金分割搜索策略通过判断初始位置位于黄金分割点处的目标是否可使导弹构成攻击条件,即导弹是否能够在满足3.5节所提到的多约束条件下命中目标,并根据搜索任务的不同,沿数轴向左或向右收缩搜索区间。在远边界搜索中,初始位置在分割点处的目标,导弹不构成攻击条件时,搜索区间将以分割点为界沿数轴左侧收缩;当构成攻击条件时,搜索区间以分割点和原搜索区间右边值为界沿数轴右侧收缩。在该搜索策略中,导弹对初始位置位于黄金分割点处的目标是否具备攻击能力直接影响下一步的搜索方向与区间选择,因此搜索区间的设定对发射区边界的解算结果影响极大。实际解算中,初始搜索区间预估困难,可能导致难以输出完备的可发射区解算结果。 以远边界搜索为例,假定可攻击距离真实取值区间为[Nt,Ft],远边界值初始搜索区间为[a0,b0],第i次循环的搜索区间为[ai,bi],黄金分割值为Ri。存在以下2种情况使搜索值输出无效: ①导弹对黄金分割点处的目标不具备攻击能力。此时,前一循环的黄金分割点Ri-1不属于可发射区真实取值区间,且当前循环的黄金分割点Ri小于真实可发射区间左边值Nt。即: (15) 式中:i≥1。此时远边界值沿数轴左侧持续搜索,最终不存在可攻击距离值输出。假设取值足够小,随取值不同,又可分为不同的状况子集。设i=1满足式(15),具体状况可阐述为: 初始搜索区间右边界值大于远边界实际值,黄金分割初始值小于近边界实际值; 初始搜索区间右边界值小于近边界实际值; 初始搜索区间右边界点介于远边界与近边界值之间,初始黄金分割值小于近边界实际值; 初始黄金分割值大于远边界实际值,二次黄金分割点小于近边界实际值。如图3所示。 ②导弹对黄金分割点处目标具备攻击能力,但初始搜索区间取值不合理,使区间右边界值小于远边界实际值,如图4所示。此状况只存在于初始分割点处目标可使导弹构成发射条件的情况。即: 此时,远边界输出值为初始搜索区间右边界值b0。近边界搜索存在的问题与远边界类似,在此不做赘述。 针对上述提到的两类问题,本文设置外层循环,通过自适应修正初始搜索点,实现边界值的二次搜索:首先对搜索输出结果进行评估,当满足边界输出值为0或远界输出值等于搜索范围边界值时,执行外层循环。通过平移初始搜索点,对初始搜索范围进行动态修正。假设动态修正距离为d,最大动态修正次数为s,则基于目标机动预估的远边界搜索流程如图5所示。 由于修正了初始搜索范围,在d取值合理的情况下,第②类问题易于解决;对于第①类问题,通过边界值动态重复搜索,极大地降低了导弹误判不存在可发射区间的概率。当修正次数达到最大修正次数s时,若导弹仍无法命中目标,则认为在该态势下导弹不存在可发射距离。目标进入角为180°,以侧向过载为4执行匀速右转弯机动的条件下,在相同初始状态,2种算法所求得的可发射区对比仿真结果如图6所示。可见本文提出的改进方法相较传统的黄金分割法在发射区域面积上有了明显提高。 由于只对无效输出的情况进行修正,本文算法在保证求解精度的同时,在解算时间上与原搜索算法无太大差异。解算时间与修正次数、角度划分粒度及修正距离等方面存在相关性,因而要在解算精度与求解速度方面进行权衡。 以初始时刻目标进入角为0°作为算例。选取某型导弹的气动参数和相关数据,导弹最大离轴发射角为60°,发射后最大动态视场角为70°;导弹可控飞行时间为20 s,最大飞行时间为27 s;引信可靠作用距离为7 m;导弹最大可用过载为40;比例导引系数K取值为3。发射时刻,载机位于坐标原点,Ma=0.8,高度为5 km,航向角为0°,航迹倾角为0°;导弹速度与高度大小与攻击机保持一致,且假定已完成发射前的相关准备;目标与载机位于同一高度的水平面内,初始时刻以Ma=0.8做匀速直线飞行,最大侧向可用过载为6。 远边界初始搜索范围a0=0,b0=25 km,动态修正距离为d=5 km,最大修正次数s=10;近边界初始搜索范围a0=0,b0=5 km,动态修正距离d=0.5 km,最大修正次数s=8。 ①目标保持原运动状态,以侧向过载nm,x为0,nm,z为1,做匀速直线飞行。根据图5给出的解算流程,导弹的可发射区解算结果如图7所示。图中处于中心位置,坐标为(0,0)的是攻击机,散布于攻击机四周的是目标机;靠近攻击机的三角部分连线为近边界,远离攻击机的圆连线为可发射区远边界。在导弹轴线-60°~60°的离轴角范围内形成封闭的包络。 ②导弹的不可逃逸区。目标在其极限过载所允许的,过载范围为[0,6]的区间内,以等梯度变化值为1,向左或向右实施水平等速转弯机动。遍历该范围内的7个过载值对应的13个状态,通过图5给出的解算流程,计算所有状态下可发射区的公共交集作为不可逃逸区。导弹不可逃逸区的解算结果如图8所示。 ③基于目标机动预估的可发射区。从战术层面进行目标机动预估,由于目标进入角为0°,因此,目标方位角为正时,预估目标实施左转弯逃逸机动;目标方位角为负时,实施右转弯机动。为了快速摆脱导弹直接瞄准,假定目标以最大过载逃逸,导弹的可发射区如图9所示。 3种发射区的比较结果如图10所示。由图可知,在目标进入角为0的相对态势下,不可逃逸区的可攻击面积最小,本文提出的基于最大概率机动预估的可攻击面积最大。对于载机前方一定角度范围的目标,本文提出的发射区相较另外2种发射区在发射区域面积上有了较大范围的提高。这主要是由于目标实施逃逸机动时,目标沿y轴方向的速度分量减小,导弹与目标沿y轴方向的相对速度增大,从而使该方向的远边界值向高值方向延伸。当目标方位角绝对值大于36°时,基于目标机动预估的发射区,较目标保持原运动状态时的可发射区,在远边界上有所减小。这主要是由于目标方位角增大时,导弹受动态视场角的影响程度有所增大,导弹可攻击的距离减小。这也从侧面证明,目标沿远离攻击机机身轴线方向实施逃逸机动的有效性。 在文中给出的速度、高度等初始状态下,不同目标进入角时,3种形式的发射区实时在线解算时间如表2所示,所有解算过程均在Windows 7系统、主频3.2 GHz,内存2.96 GB的PC机上,采用Matlab R2013a编程实现,每种状态均进行20次实验重复,并记录其平均解算时间。从解算时间上看,本文提出的可发射区与保持原运动状态的可发射区基本一致。相较于考虑任意机动状态的不可逃逸区,解算时间大大减小。 目标沿导引头视线方向远离攻击机、目标与攻击机视线方向成90°夹角和目标进入角为90° 3种目标初始状态下,不同表示形式的发射区,在发射区域解算面积上的对比结果如图11所示。综合图10和图11可知,速度、高度等初始条件相同的情况下,初始态势不同,3种发射区的解算结果也存在很大差异。整体来看,本文所提出的基于目标机动预估的可发射区相较于传统的不可逃逸区,可攻击范围有了较大提高,解算时间大大降低,有利于充分发挥导弹的战术使用性能;与传统的可发射区相比,解算时间基本一致,但由于对目标机动有了一步预估,更符合空战对抗实际,因而具有更广泛的应用价值。 表2 不同相对态势下3种可发射区解算时间 s 本文提出了基于目标机动预估的空空导弹可发射区的新概念,并系统论述了概念的含义;基于多种实际约束,建立了导弹、目标和相对运动模型;针对黄金分割搜索算法的不足,提出了改进办法;并利用改进的黄金分割搜索策略实现对基于目标机动预估的可发射区进行了快速解算。仿真结果表明: ①基于目标机动预估的空空导弹可发射区在攻击面积上明显大于不可逃逸区;在实时解算时间上远小于不可逃逸区,且其解算时间与保持目标原运动状态的可发射区基本一致。 ②基于目标机动预估的可发射区相较于目标保持原运动状态的可发射区在攻击面积上不存在相关性,二者区域面积的大小关系与目标机初始时刻运动方式有关。 ③基于目标机动预估的可发射区由于对目标运动状态进行了一步预估,因而该可发射区有利于更好地适应空战中剧烈的态势变化。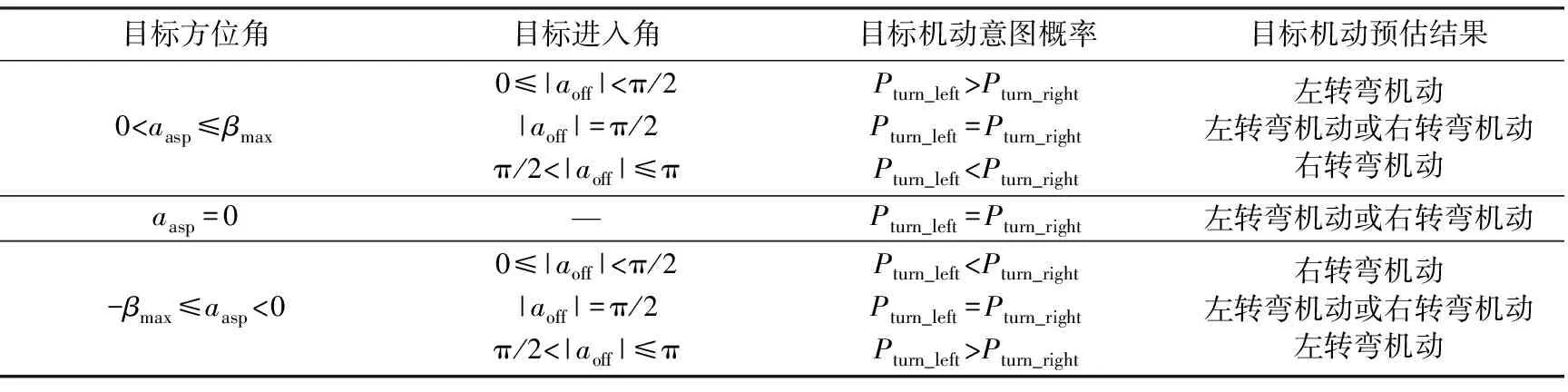
3 空空导弹、目标、约束模型
3.1 空空导弹运动动力学模型

3.2 导弹导引控制模型
3.3 目标运动模型
3.4 导弹-目标相对运动模型
3.5 导弹性能约束条件分析

4 基于改进黄金分割搜索算法的可发射边界求解策略
4.1 黄金分割策略的基本原理
4.2 黄金分割搜索策略的不足
4.3 黄金分割策略的改进办法
5 模型验证与仿真分析
6 结论
