基于瞬态启车数据的透平机械叶片健康监测方法*

张 娅 陈 康 王维民 屈 维

（1.压缩机技术国家重点实验室;2.北京化工大学 高端机械装备健康监控与自愈化北京市重点实验室）

0 引言

旋转叶片是通风机、鼓风机和透平压缩机等机械进行能量转换的核心部件，其工作安全与工作效率对机组的平稳运行意义重大。振动问题一直是限制透平机械向大型高参数化方向发展的主要障碍，而叶片振动导致的疲劳断裂故障和事故尤为突出，因此，对叶片的状态参数进行监测极为必要。叶片振动测量主要有接触式和非接触式两种方法[1]，叶尖计时法作为非接触式测量方法是目前叶片测振领域的研究热点。目前国际上公开且有效的基于叶尖定时法原理的叶片振动参数识别算法主要有单参数法[1]（非线性最小二乘拟合法或速矢端迹法）、双参数法[2]（又称椭圆拟合法）、正弦拟合法[3]（包括三参数、四参数、六参数法）、自回归法[4]（AR法以及基于其发展而来的GAR法及GARIV法）、Number of Aliases法[4]、基于速矢端迹法的倍频遍历法[5]、最小二乘复频域法[6]。

各个方法各有优缺点，如双参数法对信号质量要求较高，速矢端迹法无法求出倍频值，倍频遍历法需要较多的传感器才能求解出倍频值等。从机器启停车或者转速波动数据中，进行叶片的动频测量，是一种有效的进行叶片状态参数监测的方法。提出基于非线性最小二乘拟合和AR方法相结合的基于叶片同步振动的叶片状态参数精确辨识方法，模拟和实验研究结果表明，该方法具有在所测试的转速范围内，可以达到0.02%的精度。

1 风机叶片振动频率辨识方法

基于叶尖定时法原理的叶片振动监测经过多年的研究，已经基本上可以进行叶片的振动幅值、频率、恒偏量、阻尼等测量，并取得不少成果[7-10,12]。本文基于现有的成果并结合工程实际需求提出的基于一次启车或停车过程的叶尖计时法叶片振动数据，采用非线性最小二乘拟合法和自回归法（AR法）相结合的叶片参数识别方法。该方法具体为通过非线性最小二乘拟合法对启车（停车）过程的扫频数据进行拟合确定同步振动中谐共振点处的中心频率、幅值等参数；同时根据拟合得到的参数建立各个传感器在该共振中心频率附近的拟合曲线，截取谐共振中心附近一定范围的转速对应的拟合曲线数据，通过自回归法（AR法）分析获得对应谐共振中心的倍频值，进而获得较为完整的叶片同步振动参数。本方法的提出可在传感器使用的数量上减少到4支，安装的位置较为紧密，传感器夹角较小，且可以获得较高的参数辨识精度。

1.1 新的固有频率的识别方法

基于扫频拟合和自回归法的叶片同步振动参数辨识流程如图1所示。

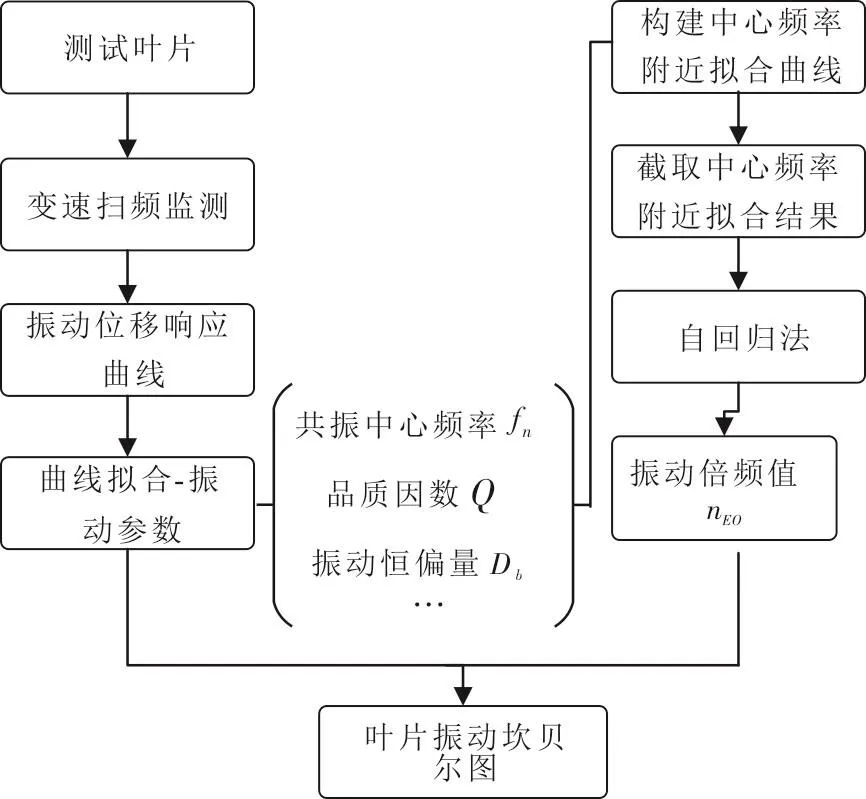
图1 叶片同步振动参数辨识流程图Fig.1 Flow chart of blade synchronous vibration parameter identification

首先需要通过变速扫频监测叶片的振动位移随转动频率之间的变化情况，进而确定发生的同步振动区间。截取不同传感器采集到的同一编号叶片的谐共振区域分别进行参数拟合，获得叶片同步振动参数，扫频过程传感器采集的同步振动信号曲线拟合法拟合目标函数[11]为：

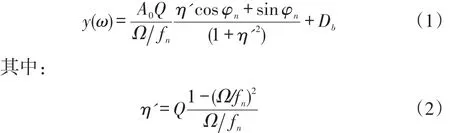
式中记Q=1/(2ξ)表示品质因数；fn称为谐共振中心频率，Db表示叶片振动存在的振动恒偏量，式（1）中共有5个待求解未知量，即A0,Q,fn,Db,φn，通过变速扫频过程可以获得叶尖振动位移随转频的变化关系y(ω)，由式（1）可根据LM法来求解上述未知量，同时根据得到的参数建立在各个叶片各个传感器在该共振区间的拟合曲线，截取谐共振中心附近一定范围的转速序列对应的拟合结果，通过AR法分析四个传感器的拟合振动序列获得对应谐共振中心的倍频值。根据自回归法原理[4]，假设四支安装间隔夹角相等的叶顶传感器监测得到的振动位移依次为x1，x2，x3，x4，最终求解的方程（3）中含有两个未知数，即a1及振动恒偏直流分量xDC。

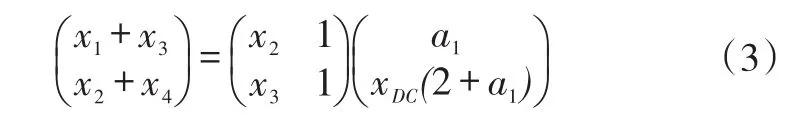
解出a1值并结合a1=2cos(ωnΔtp)可得到叶片振动频率ωn值。叶片同步振动过程中谐共振中心对应的倍频值可表示为

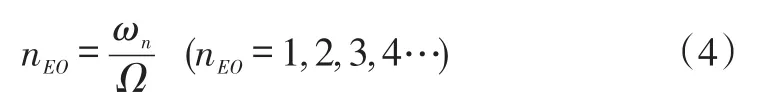
其中Ω运转转频值（单位：Hz）。将a1=2cos(ωnΔtp)带入式nEO=ωn/Ω中可得：

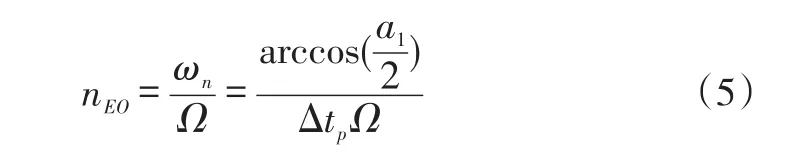
当传感器等间距分布之间的夹角为α时，则Δtp表示为：

带入式（2）可得：

推导中假设叶片组运转转频为谐共振中心处转频，通过分析式（7）可知该运转转速对振动倍频的求解没有影响。因此可以认为只要a1值的求解准确，则在不同的谐共振中心频率都可以准确求解出振动倍频值。先前研究[7-8,12]表明在谐共振中心频率附近恒速运转使用上述方法同样有效，而当转速在小范围内发生上升或下降可近似认为是一个恒速但有转速波动过程，其4支传感器采集到的振动信号依旧满足式（3）所示关系，所以扫频过程中可同样适用，并在后续模拟仿真及实验得到验证。

当阻尼系数很小时，可以由式（8）求得叶片在共振中心频率的振动幅值Amax:

最后可根据拟合获得的谐共振中心频率、振动幅值等参数，结合式（9）计算叶片的振动频率，做出叶片振动坎贝尔图。

2 对新算法的模拟仿真验证

2.1 仿真模型的建立

在相关领域中实际使用的叶片结构复杂，可以认为有无限多个自由度，无法使用数学表达式表达其复杂的结构特征及运动特性。通过有限元分析能有效地解决这一问题，对叶片的振动进行必要的简化，有助于进一步应用于叶尖计时分析。以下将通过有限元方法建立叶片振动的数学模型。

多自由度叶片受迫振动微分方程可以表示为：

式中M，C，K分别表示整体结构的质量矩阵、阻尼矩阵和刚度矩阵，f(t)表示激励向量，q表示多自由度的叶片振动位移。每个叶片受到的激振力函数可以表示为：

式中,Fb为激振力幅值常量;nEO为叶片振动倍频值;Ω为转子系统运转转速值;b为叶片编号;φ为叶片b的延迟相位。

本文所用到的多叶片振动系统模型图如图2所示，每个叶片有自身的质量、刚度以及阻尼，同时相邻俩叶片之间不存在耦合，即叶片间互相独立。

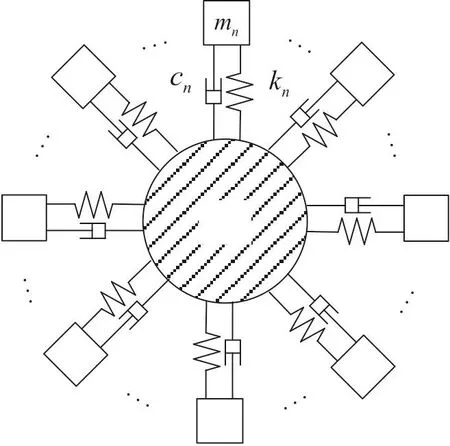
图2 多叶片振动模型（激振力无示出）Fig.2 Assembly model of multi-blades vibration(forces not shown)

建立叶尖计时振动采集模型，具体过程国内外文献[4,10]已有较多介绍，故不在此介绍。

建立4个叶片振动模型，各个叶片参数设置相同，仿真中涉及参数设置如表1所示：

表1 相关参数设置Tab.1 Related parameter settings

2.2 算法的模拟仿真验证

2.2.1 不同信号质量（高斯白噪）对辨识精度的影响

模拟启车过程，转速从0Hz升速到120Hz，升速速率为2Hz/s。采用4支传感器，夹角6度均布（与现有实验台相同）。

通过4支传感器对4个叶片进行叶尖振动信号采集，并对模拟采出信号进行分析，分为3种情况进行对比，即无噪声理想信号，信噪比为0.8的信号，信噪比为0.6的信号。所添加噪声为高斯白噪声，具体添加方式为：

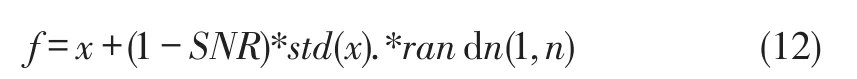
其中：x表示理想仿真所得的传感器信号数据；SNR表示信噪比，其取值范围为SNR∈(0,1]，SNR越大，信号质量越好；n为信号长度；f为添加高斯噪声后的信号数据。

以下以1号叶片为例进行说明。

对以上三种情况的数据进行分析，首先截取各个振动中心附近的数据进行最小二乘法拟合。分别截取0到40Hz（区间a）及60到100Hz（区间b）进行拟合，图4所示为1号传感器所得的信噪比为0.6的数据的拟合情况。

对不同传感器采集的数据在不同信号质量下进行拟合分析并求取平均值，共振中心频率拟合结果如表2所示：

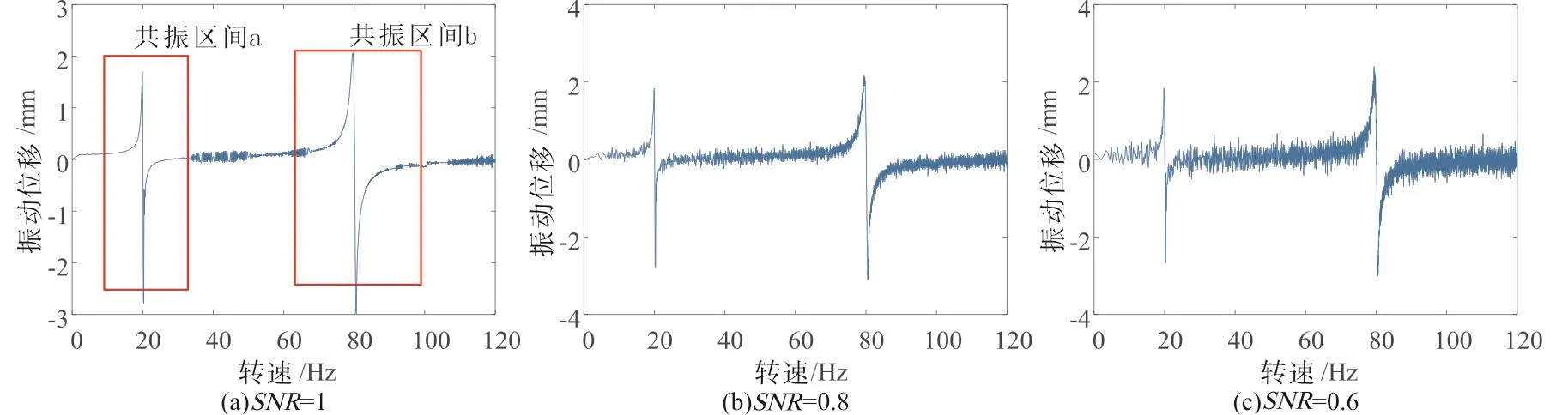
图3 一号传感器不同信号质量下的启车数据Fig.3 Data under different signal quality gathering by No.1 sensor

图4 SNR=0.6时两个共振区间拟合曲线与采样数据对比Fig.4 Comparison of Two Resonance Interval Fitting Curves and Sampling Data

表2 1号叶片拟合结果Tab.2 Fitting results of No.1 blade

截取共振区间共振中心附近的数据进行自回归法（AR）求取倍频值，共振区间a截取范围为19.9～20.3Hz，共振区间b截取范围为79.5Hz到80.5Hz，转速数据点间距均取0.01Hz。图5所示为信噪比为0.6时分析的拟合2曲线。倍频求解结果如下表3：

以上圆整后求得的倍频数分别为20和5。

图5 自回归法所截取的拟合数据Fig.5 The fitting data intercepted for AR method

故综合以上分析计算不同信号质量下求得的叶片的固有频率及误差，如下表4所示：

由表4可知，该方法在不同信号质量下表现稳定，且误差较小，共振中心b处数据求解所得的误差甚至在2‰以内，所以可以认为本文所提出的方法是有效的。

2.2.1 不同升速速率下对辨识精度的影响

同样进行0到120Hz的升速，分别进行上升速率为1Hz/s和0.5Hz/s的扫频分析，均不添加白噪声。

分析操作同上小节相同，辨识结果如下表5所示：

以上均可以认为所求得的倍频数分别为20和5。

故综合以上分析计算不同信号质量下求得的叶片的固有频率，如下表6所示：

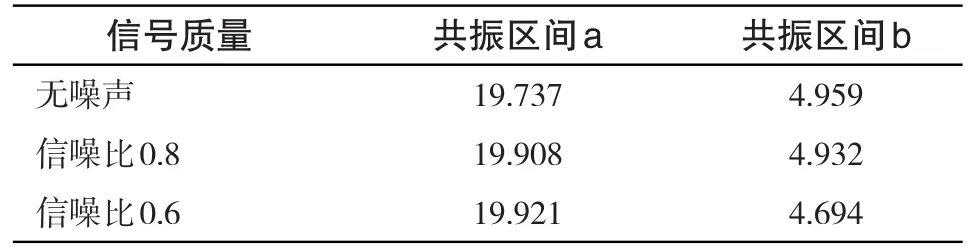
表3 1号叶片倍频求取结果Tab.3 Solving the EO of No.1 blade

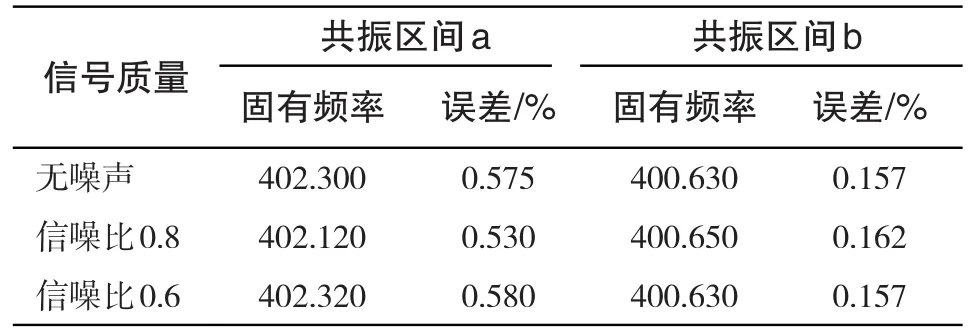
表4 固有频率求取结果及误差Tab.4 Natural frequency and deviation

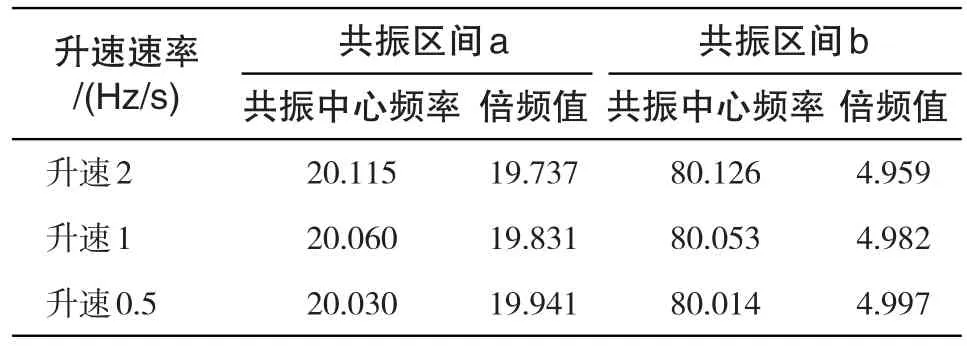
表5 叶片参数识别结果Tab.5 Result of blade characteristics

表6 叶片固有频率求取结果及误差Tab.6 Natural frequency and deviation

通过对比可知随着升速速率的下降，本文所述的方法的求解精度不断上升，且在0.5Hz/s的情况下对共振区间b进行求解的误差小于万分之二。同时需要说明的是在多次相同原始数据的基础上添加高斯白噪所得的数据进行倍频求解的过程中，还发现当转速上升速率过高时，对倍频值的求解影响较大，可能偶发求解不准的情况。以上现象的原因在于随着转速上升速率的不断增加，在相同的转速区间内所能采集到的数据就越少，可供分析的数据量也就越小，由此导致采集过程中的噪声干扰对最小二乘拟合法和自回归法的影响增大，进而所得的固有频率（动频）的误差也将增大。对于共振区间a与共振区间b之间求解结果的误差相差较大同样也与转速相关，由于共振区间a附近的转速较低，每分钟所转过的圈数也就相对于共振区间b来说要少的多，而叶尖计时原理可知对于单个叶片每旋转一圈仅经过一次传感器，即传感器采集到1个脉冲信号，因此相同情况下共振区间a内的数据量要比共振区间b内的要小得多。因此在实际的应用中需要尽可能地采集更多的数据，即需要选择合适的升速速率。

3 实验研究

3.1 实验台及测试系统

验证识别算法所采用的高速直叶片振动实验台的具体细节和整体概貌如图6所示。试轮盘外安装兼做传感器支架的护罩，护罩周向开有若干个等角度（6°）传感器安装孔，护罩顶部开有12个永磁激励部件安装孔。激励部件内嵌一个钴基永磁铁以提供激振力，通过调整部件数量及分布情况，可开展若干组合下的激励测试实验。

图6 高速直叶片实验台和测试系统Fig.6 High-speed straight blade test bench and testing system

测试系统至少需要激光源通道数为5个（其中1个通道用于键相、4个通道用于叶尖计时，剩余备用）。叶顶光纤传感器的安装要求为间隔夹角6°，为实现实验中转速控制，通过模拟输出卡对变频器进行输出控制，可按设定参数进行升降速运转、恒速运转等。

本实验台叶轮的剖视图如图7(a)所示，在叶片根部进行叶片局部减薄以期降低叶片的固有频率，该结构局部放大图示于图7(b)。轮盘俯视图如图7(c)所示，整个轮盘由32个叶片组成。根据键相的位置和叶轮实际运转方向对叶片进行了编号，如图7(a)中红色数字所示。

图7 叶轮结构图及叶片编号Fig.7 Impeller structure and blade number

用ANSYS软件对其模态进行分析，得到叶片部分振动坎贝尔图，如图8所示。一阶振动频率为2 285Hz（转速为7 000r/min时的预应力模态）。该值可以粗略估计谐共振出现时的运转转频值。

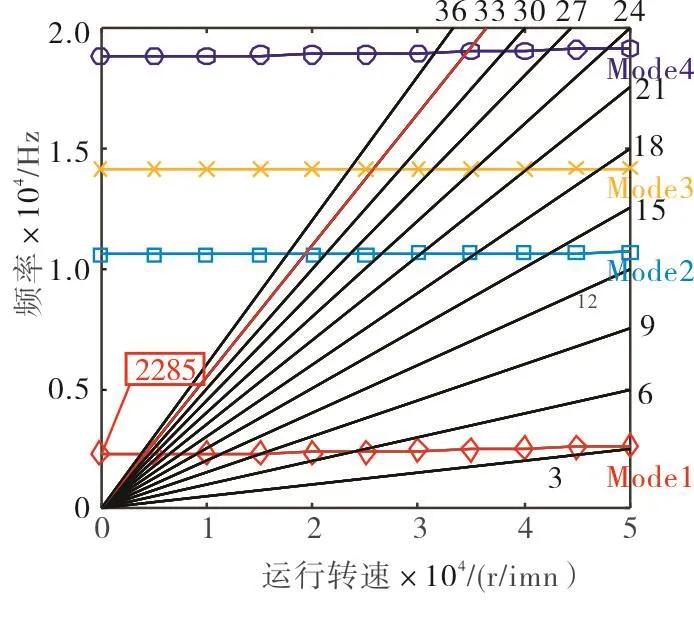
图8 高速直叶片振动坎贝尔图Fig.8 Campbell diagram of high-speed straight blade

3.2 实验及数据分析

实际的实验测量与模拟仿真之间有较大的差距，如在模拟仿真中可以直接获得较为准确的叶片振动位移值，但在实际的测量过程中，叶片的振动位移需要通过叶尖定时技术测量来获得。已知叶尖定时测量最重要的是获得实际到达叶顶传感器的时间与理论到达传感器的时间差值来求取叶片振动位移。但实际测量过程中理论到达时间的确定是非常难的，针对本实验台采用动态标定法标定理论到达时间[7]。实验中对叶片同步振动参数辨识流程进行了实验测量，实验台周向均布安装12个磁铁激励，进行分析的运转转频范围为75～132Hz，采用的升速速率为1Hz/s，通过四个叶顶传感器监测的5号叶片振动位移随转频的变化情况如图9所示。

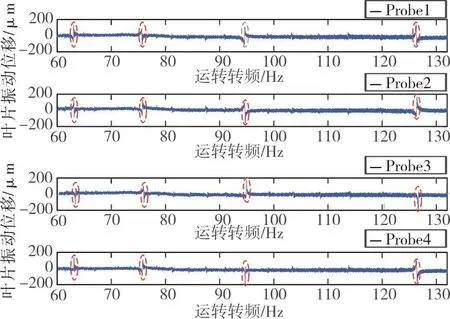
图9 四支传感器监测到的5号叶片振动位移响应情况Fig.9 The vibration displacement response of No.5 blade monitoring by four sensors

如图9所示，叶片在该段运转区间内被激起的谐共振区间有7个，图中用红色圆圈标记。分别对各谐共振区间段截取拟合，以下将以振幅最大的谐共振区间（图9中左起第3个红圈所示）为例进行说明。

3.2.1 LM拟合

截取4个传感器采集到的对应于5号叶片从92Hz到96Hz的振动数据进行拟合，拟合效果如下图10所示：

拟合结果如下表7。对振动中心频率求平均为93.729Hz。

3.2.2 倍频求解

根据拟合结果，构建4条对应的拟合曲线，如图11所示，截取共振中心93.729Hz附近的拟合曲线上的数据点进行自回归法（AR）求取倍频值，范围为93.6Hz到93.8Hz，数据点间距取0.01Hz。得到的结果为23.950 5，圆整后为24。

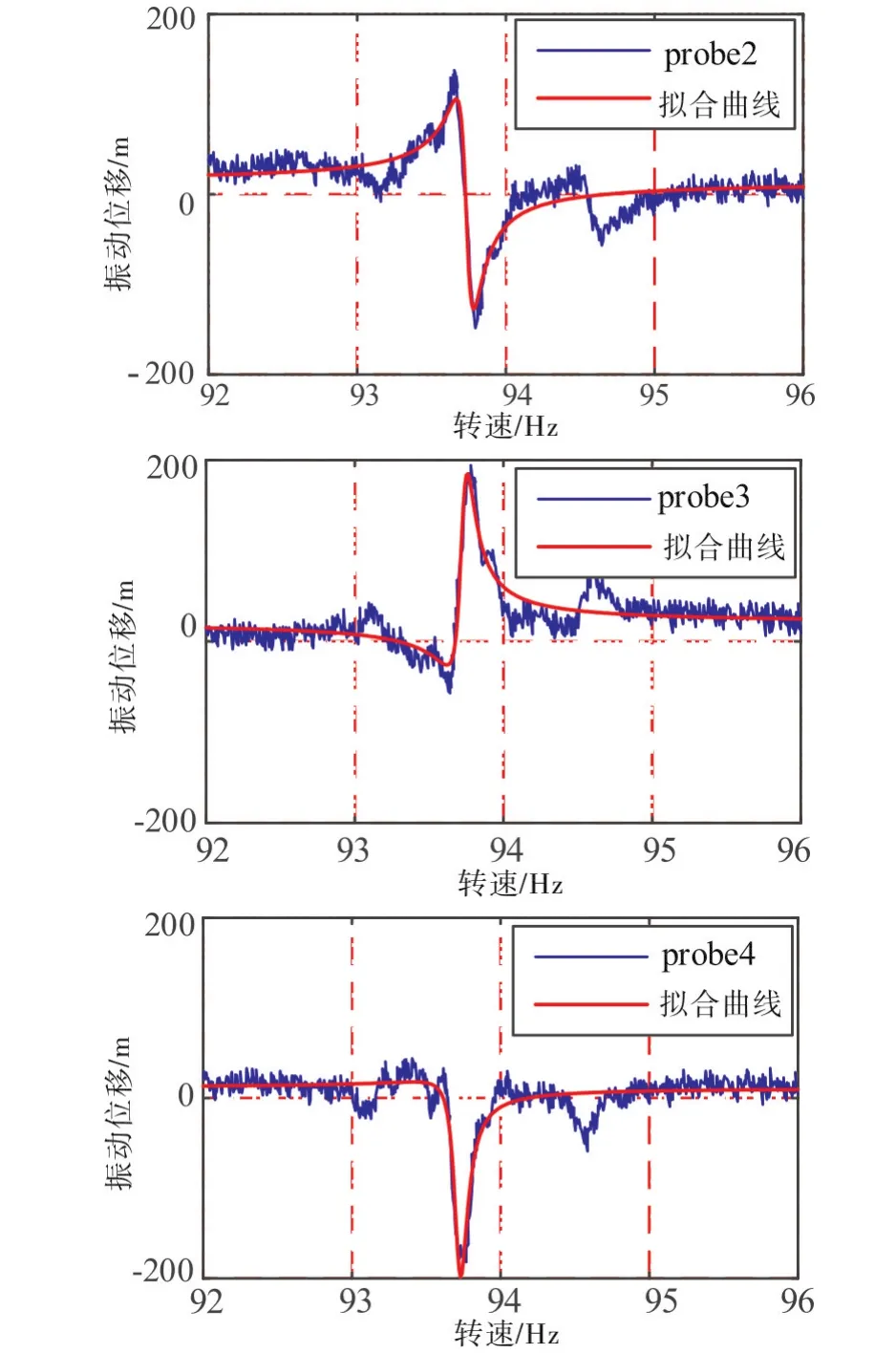
图10 四支传感器监测到的5号叶片振动位移拟合情况Fig.10 Curve fitting of vibration displacement response of No.5 blade monitoring by four sensors

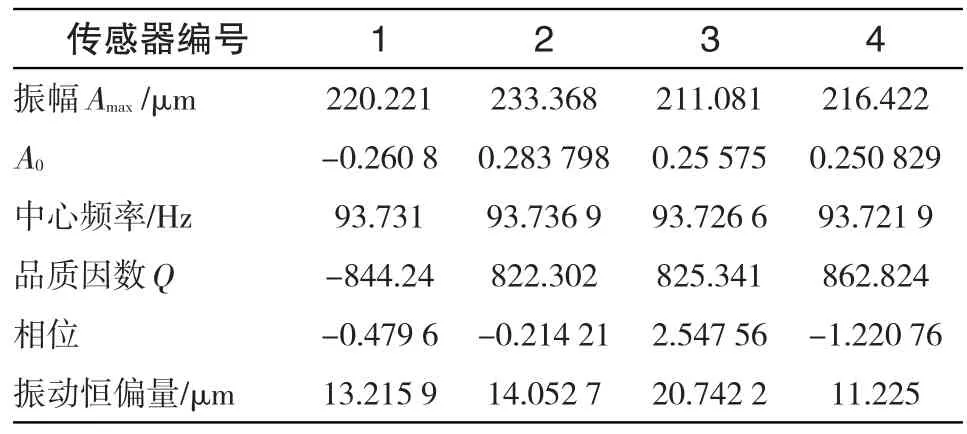
表7 拟合结果Tab.7 Fitting result

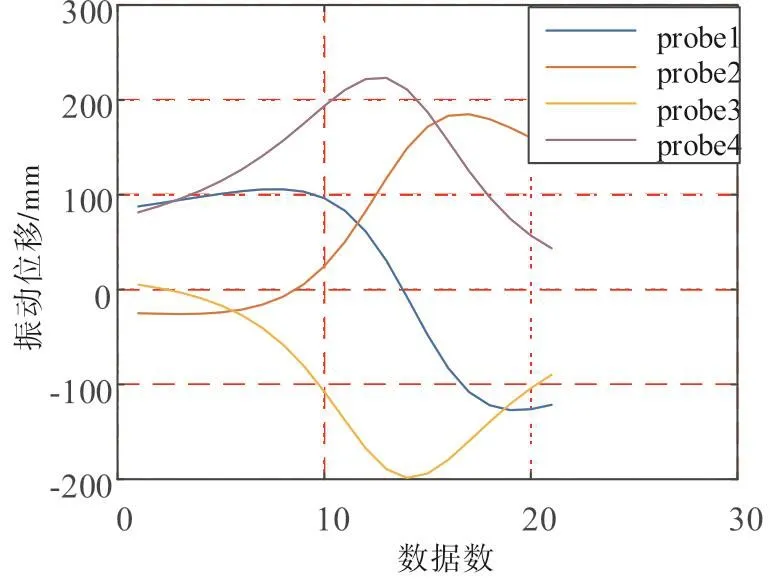
图11 自回归法截取的数据Fig.11 The fitting data intercepted for AR method

3.2.3 综合各个共振区间的求解结果

截取各个谐共振区间进行分析，分析过程及结果见表8。由表8可以看出，通过本文所述方法求解得到的叶片振动频率基本相等，同时随着倍频值的降低叶片振动频率值呈现出逐渐增大的趋势，这是由于转子叶片随着转速的增大，叶片的离心刚度增大，进而导致叶片振动频率增大。

表8 整体分析结果Tab.8 Results of overall analysis

4 结论

通过模拟仿真及实验，验证了本文提出的基于瞬态启车数据的叶片健康监控方法的可行性，实现了通过分析单次启车或停车的叶尖振动信号得到叶片振动参数。减少传感器数量到4个，模拟仿真结果显示共振中心在4 800r/min左右，升速速率为30r/min/s时，本文所提出的方法可以达到万分之二的测量精度，同时实验分析各个共振区间得到的振动频率之间的相对误差在千分之三以内，说明了辨识方法的准确性，可以用于辨识叶片的健康状态。