Perfect Gas Approximation of Real Gas Behavior of an Organic Working Fluid Applied in the Aerodesign Simulation of a Radial-inflow Turbine

（Turbomachinery and Engine Technology Dept.,Product Development Center,IHI Corporation,Shin-Nakahara-cho,Isogo-ku,Yokohama 235-8501,Japan）

Abstract:Today the Organic Rankine Cycle(ORC)is considered as one of the most promising technologies to recover the power from low-grade heat resources.In order to realize a high performance ORC turbine,the Computational Fluid Dynamics(CFD)is extensively used to simulate the internal flow in the aerodynamic design.But due to the high non-ideality of the working fluid,it is crucial to take the real gas effect into consideration.In the present study,an accurate and reliable method of the perfect gas approximation for an organic working fluid(R245fa)is developed.At first,the effectiveness of a perfect gas approximation is examined in two-dimensional CFD simulations of a convergent-divergent nozzle.Then the accuracy of the perfect gas approximation,definition of suitable nondimensional performance parameters and effective conversion method between the different gas models are studied in three-dimensional CFD simulations of an ORC radial-inflow turbine.

Keywords:Organic Rankine Cycle(ORC),Radial-inflow Turbine,Organic Working Fluid,Real Gas Effect,Perfect Gas Approximation

Nomenclature

Subscripts

1 Introduction

Recently industrial/governmental/municipal efforts to recover the power from low-temperature heat resources are getting more intensive than before due to the increasing interests in more sustainable society.Among many innovative technologies,the Organic Rankine Cycle(ORC)power generation is considered as one of the most promising ones for this purpose.For medium or large ORC generators,a radial inflow turbine is suitable for its ruggedness and relatively simple construction,with an organic working fluid in a binary system.Due to the high non-ideality of the working fluid,it is crucial to take the real gas effect into consideration.Although most current meanline performance prediction tools and commercially available Computational Fluid Dynamics(CFD)tools are capable of incorporating real gas models,simulations with such a gas model tend to be more time-consuming than those with a perfect gas model in terms of both CPU time and manual post-processing time.Further it can be unstable due to the simulation near the saturation boundary.Therefore simulations with a perfect gas approximation are still an attractive option to stably and swiftly conduct design tasks.

Harinck et al.(2010)[1]carried out a comparative study of gas models with different degrees of fidelity,such as the polytropic ideal-gas(PIG),the Peng-Robinson-Stryjek-Vera(PRSV)and high-accuracy multiparameter equation of state(MPEoS).CFD simulations on an axial-flow turbine nozzle operating at subcritical/supercritical conditions were conducted,with R245fa as one of the working fluids examined.It was shown that the perfect gas approximation is advantageous in terms of the computational cost,but the deviation of the blade surface isentropic Mach number from that with MPEoS was unacceptably high,as high as 5%at the subcritical condition.For the supercritical condition,the deviation doubled.In this research,the specific heat ratio of PIG was defined on the basis of the gas constant(the universal gas constant divided by the molar mass)and the low-pressure isobaric specific heat evaluated at the critical temperature.

Another issue associated with the gas modeling is the way the performance parameters should be converted to the actual intended condition when they are acquired in a simulation with a different working fluid than the intended one,or vice versa.Walsh and Fletcher(2004)[2]suggest using a set of non-dimensional parameters to convert the performance,such as the tip Mach number,the flow coefficient,the isentropic load coefficient and the efficiency.Roberts and Sjolander(2005)[3]took a similar way for a centrifugal compressor but developed a method to correct the effects of the different specific heat ratios.ASME PTC-10(1997)[4]requests to use the density ratio,the flow coefficient,the load coefficient and the efficiency for the conversion of the compressor performance.Similarly,Macchi and Perdichizzi(1981)[5]suggest the use of the density ratio to accurately correlate the performance of the axial-flow turbines.Von Backström(2008)[6]described a translation of the compressor characteristic by means of the density ratio.

Some past researches focused on the accuracy and the cost-performance of the perfect gas approximation.Nevertheless,due to less proper definition of the perfect gas properties and/or the less physical evaluation of the resulting performance and fluid dynamic parameters,the validity and the effectiveness of the perfect gas approximation have been evaluated wrongfully low.Some researches compare the dimensional parameters directly,such as the pressures obtained by two different gas models.Other researches confuse the meanings of the isentropic exponent and the specific heat ratio,or use a physical gas constant without taking the compressibility factor into consideration.In the present study,it is intended to provide a way to approximate the real gas nature of an organic working fluid(R245fa in this study)as a perfect gas in more physically meaningful manner.Problems in the approximation in the aerodynamic design of the ORC turbine were examined.The research issues discussed are(i)how to select the proper value of the isentropic exponent,and(ii)how to specify the operating condition in the fictitious perfect gas world and how to convert the resulting performance/fluid dynamic data back into the real gas world.A modern CFD simulation tool is extensively used,but at the same time,the isentropic flow theory is also used frequently to enhance the physical understanding.

2 Perfect Gas Approximation

2.1 Selection of Isentropic Exponent and Gas Constant

The perfect gas model(more rigorously,the calorically perfect gas model for which both the thermal and the caloric equations of state are“perfect”)has only two independent modeling parameters,the gas constantRand the isentropic exponentγ.Here the isentropic exponent of a general real gas is defined by

and this is equal to the specific heat ratioCpCvunder the perfect gas assumption.The isochoric/isobaric specific heats are then derived respectively asand

What we want to do here is to select a set of the gas constant and the isentropic exponent which can best approximate the specific real gas behaviour in terms of non-dimensional parameters.According to the similarity theory,the value of the gas constant does not substantially affect the non-dimensional performance and the isentropic exponent is the only gas property which enters into the problem of expressing the non-dimensional performance characteristic of the turbine with a perfect gas as its working medium.Thus,we can select an arbitrary value as the gas constant.

Now what we need to do is to select an appropriate value for the isentropic exponent so that it will give the flow solution as closely approximate the real gas one as possible.Figure 1 shows the variation of isentropic exponents of saturated vapors of some randomly selected organic compounds,such as hydrocarbons(HC),hydrofluorocarbons (HFC),hydrochlorofluorocarbons(HCFC),hydrofluoroolefins(HFO),hydrofluoroethers(HFE)and siloxanes.Generally the isentropic exponent becomes smaller at higher temperatures,gets less than unity for most fluids near the critical temperature.Fluids with a higher critical temperature tend to have lower isentropic exponents.Figure 2 shows a variation of the isentropic exponent of R245fa on thep-Tplane.It varies from place to place in a turbine,therefore it is natural to select one value which falls in the range of its variation or which represents an average.The problem is that the inlet condition of turbines can be close to the critical point where the value of the isentropic exponent can get smaller than unity.An isentropic exponent less than unity means a negative specific heat,thus in such a fluid the temperature increases while the enthalpy drops.Such a hypothetical fluid is unstable(Prigogine and Kondepudi,1999)[7].

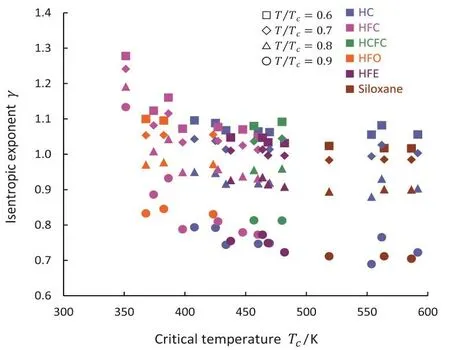
Fig.1 Isentropic exponents of organic compounds on vapor saturation conditions

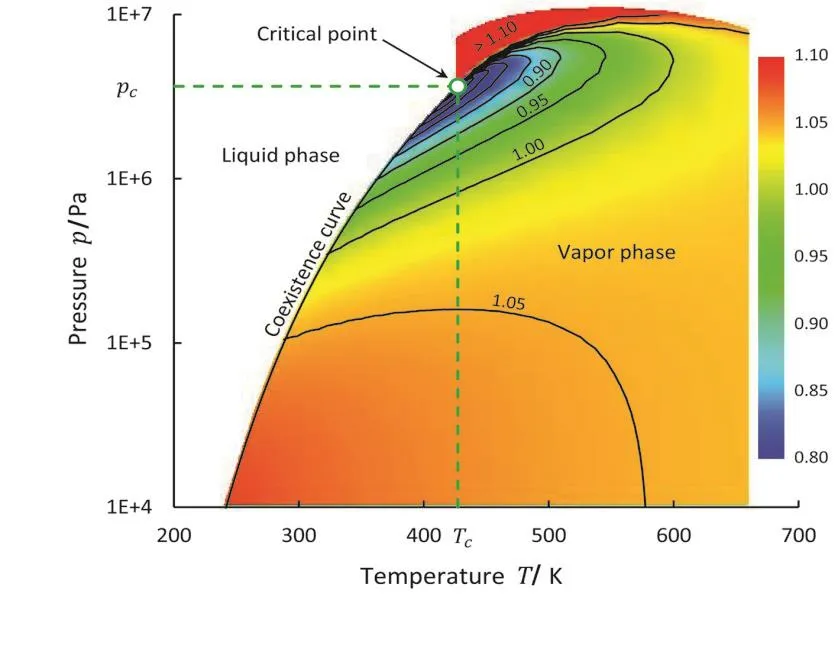
Fig.2 Variation of isentropic exponent of R245fa

The isentropic exponent of a perfect gas defines two aspects of the gas behavior.One is the isentropic relationship and the other is the caloric equation of state.In the aerodesign,the former is the more important because it dictates the mechanical interaction between the fluid and the blades.The latter predicts the temperature change through the flow which is less focused in the aerodesign.For the accurate design prediction,we must regard the former of higher importance.But for the stability of the simulation,we cannot ignore the latter aspect.From this argument,we must recognize that the perfect gas approximation is merely an engineering compromise between these two aspects.

2.2 Perfect Gas Models with Definitions of Non-Dimensional Performance Parameters

In this research,the following two methods of the perfect gas approximation are investigated,call PG2 and PG2S,respectively.In the following discussions,the parameters with a subscript“PG”intentionally express that they are used in the perfect gas condition.If with a subscript“RG”or unless specified explicitly with any subscript,it suggests that they are associated with the real gas condition or they are commonly used in both situations.

2.2.1 Perfect Gas Model“PG2”

In this first model,for the given turbine operating parametersp01,T01,p2,N,the performance parameters are defined as usual,

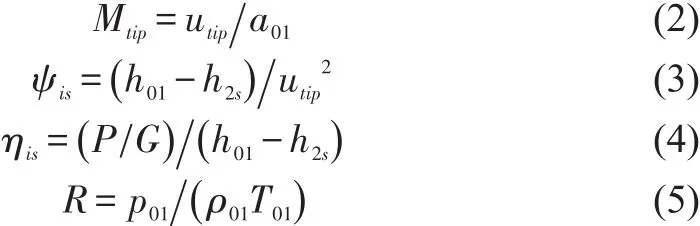
In the corresponding perfect gas world,p01andT01are set to be the same as those in the real gas.By virtue of the definition of the gas constant,ρ01is also the same.If the isentropic exponent defined by the inlet conditionwere greater than unity,we could have used the sameNin the perfect gas simulation.Unfortunately it is not true,thus we will useγdefined with the outlet condition.Consequently,the other operating parameters used in the perfect gas simulation are defined as

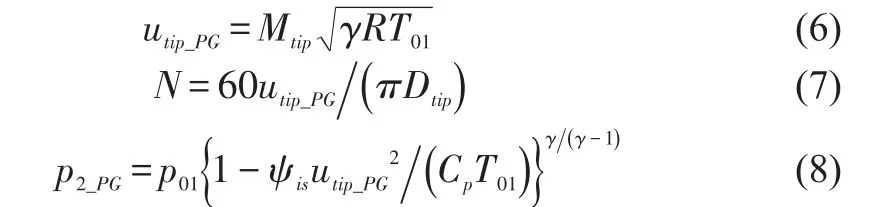
withMtipandψisas those evaluated in the real gas condition.The resulting mass flow rate should be corrected as

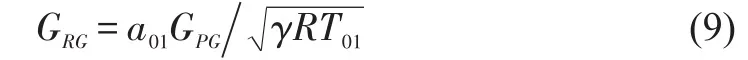
in order to compensate the inconsistent selection of the isentropic exponent.

2.2.2 Perfect Gas Model“PG2S”

In the second model the non-dimensional performance parameters are defined as follows:

In the corresponding perfect gas condition,withp2,T2s,R,γgiven as above,the relevant parametersρ2s,a2s,utip,Mtip,ψisandNhave not to be modified.The inlet total condition is specified as

The resulting mass flow rate has not to be corrected either.

Actually,in place ofp2,any pressure value smaller thanp01can be used as the reference pressure in a similar manner as PG2S and each corresponding perfect gas models can be derived.

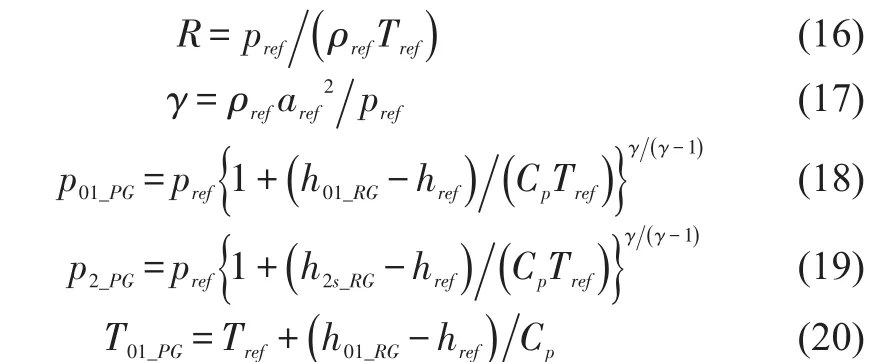
The geometric/operating parameters,like cross-sectional passage areas,flow angles,and so on,are extracted from an actual ORC radial-inflow turbine stage which will be discussed in later sections.Several perfect gas models can be defined with reference static pressure taken at some locations ranging from the nozzle leading edge(L/E)to the rotor trailing edge(T/E),and the deviations are compared.Apparently the diagonal part of the table shows lower deviations than elsewhere.It means that the deviation of each model is smallest at the location where the reference pressure is taken.

Though the isentropic calculation for Table 1 does not suffer from the instability with any value of the isentropic exponent,the actual CFD simulation cannot stably be conducted when it is smaller than unity.Actually even if it is greater than unity but still very close to the unity,the simulation can be quite oscillatory and requires longer simulation time for the convergence.So it is advisable to use a reference pressure close to the turbine exit.This is expected to be effectiveto predict more accurate power output which is directly resulting in an accurate prediction of the efficiency.In light of the above considerations,the exit condition is considered to be suitable for the reference state.

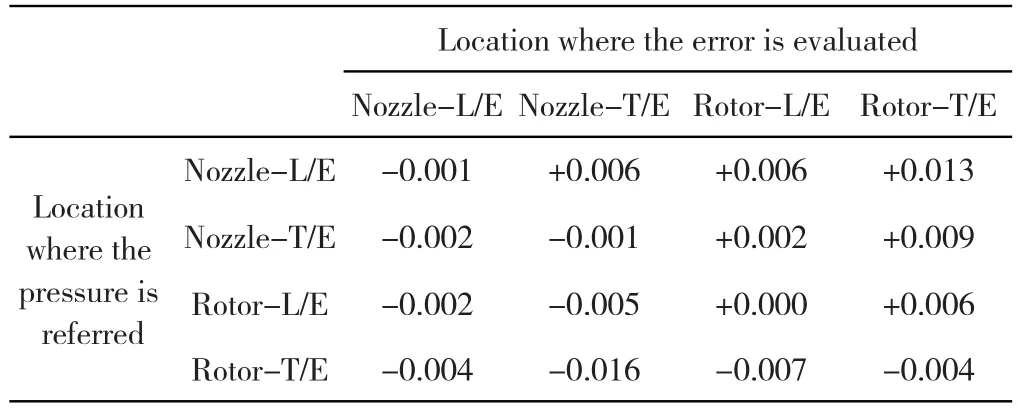
Tab.1 Deviations in Mach number in isentropic calculations

3 Validation of Perfect Gas Approximation in CFD Simulations

3.1 Evaluation of Perfect Gas Model by CFD Simulations of a Convergent-Divergent Nozzle

In order to evaluate the effectiveness of the perfect gas model over some more sophisticated models,a convergent divergent nozzle(de Laval nozzle)is simulated which has a supersonic region downstream of the throat terminating with a shock wave the upstream Mach number of which is 1.4,an arbitrarily decided value.The working fluid is R245fa and the inlet total pressure and the total temperature are set to the same values as those used for the actual turbine described in the later section.The applied equations of state(EoS's)in this study includes a perfect gas model(PG),defined in the previous section as PG2,van der Waals(VDW)model(Prigogine and Kondepudi,1999)[7],Peng-Robinson-Stryjek-Vera (PRSV)model(Stryjek and Vera,1986)[8],Soave-Redlich-Kwong(SRK) model(Soave,1972)[9]and the real gas(RG)model.The RG model is provided by NIST REFPROP.As the CFD solver,ANSYS Fluent is used.In an attempt to compare the CFD results directly with the theoretical solutions,the fluid is modeled as inviscid.A second order upwind scheme is used for the convection terms.Among EoS's used in this study,PG2 and RG are defined by means of the standard Fluent setting capabilities,while VDW,PRSV and SRK are implemented by the User Defined Real Gas Model functions.A two-dimensional axisymmetric mesh is generated with axially 120 and radially 20 equispaced divisions.The corresponding theoretical solution to each EoS is derived from the isentropic relation and the Rankine-Hugoniot relation which are applicable to general real gas EoS's.

Figure 3 compares the distributions of Mach number obtained with five applied EoS's and their deviations from the real gas solution.All models give almost identical solutions.The deviation level is highest in the neighbor of the shock wave.This is due to the slight difference in the shock position rather than due to the difference in the shock strength.

Figure 4 shows the relative comparisons of the applied EoS models.The Mach number deviation in this graph is the value evaluated at an immediate vicinity of the shock wave on the downstream side(compared not at the same place but just behind the shock wave in each solution).The deviation is defined by the difference between a solution by PG,VDW,PRSV or SRK and the RG solution,see Equation(21).Both the theoretical and the CFD results are shown here.The CFD results follow closely each corresponding theoretical counterparts,indicating that all the gas models were correctly implemented in each simulation.Generally the level of Mach number deviation is negligibly small.Even PG gives much smaller deviation(less than 2%)than those reported by Harinck et al.(2010)[1](5%for subcritical R245fa).It is quite possible that the current selection ofγvalue for PG is more appropriate than the one used by them which was selected without a detailed comparison in prediction accuracy.

Fig.3 Distributions of Mach number and its deviation from real gas solution

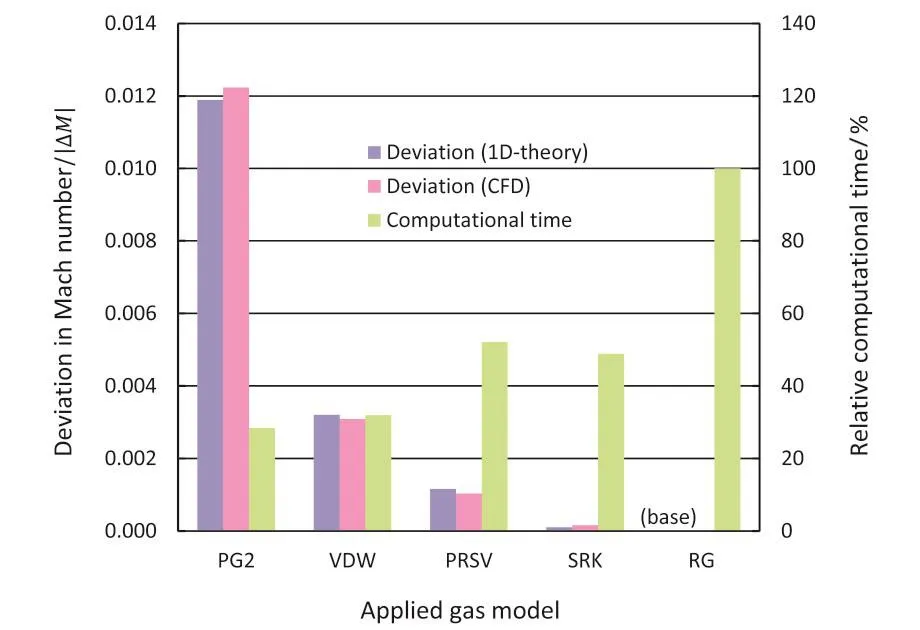
Fig.4 Mach Number Deviation and Computation Time

Also compared in figure 4 is the time consumed in each simulation.PG is very attractive in computational time.It takes only 30%of RG(actually,for a turbine stage discussed in a later section,PG takes only 10%～20%of RG).VDW is a good compromise between the perfect gas approximation and more sophisticated models.With this model,a great amount of the improvement in accuracy can be achieved at a very small increase of computation time against PG.PRSV and SRK give essentially the same solution as RG with the half computational time.REFPROP is one of the most accurate gas property prediction tools,thus it must be designed with the accuracy and the robustness as the top priority.Such an accuracy level can be attained with a cost of a high computational loading.That is why RG requires such a long computational time.But for the most aerodesign purposes,PRSV and SRK(or even VDW)may be considered to be sufficiently accurate.PG is less accurate though its accuracy level is well acceptable in the most design purposes,while the computational burden is greatly reduce.

From the above arguments,it can be said that the application of the perfect gas approximation in the turbine design is promising if the accuracy against the real gas solution is sufficiently high.

3.2 Validation of Perfect Gas Models by CFD Simulations of an ORC Radial-Inflow Turbine

3.2.1 CFD Simulation Method

A CFD validation study about the usage of the perfect gas models described in the previous section was conducted against an actual ORC radial-inflow turbine stage.This turbine stage has a volute casing,a vaned nozzle and a semiopen rotor as its constituting sub-components.In the CFD simulations only the nozzle and the rotor are three-dimensionally modeled and the volute is substituted by a one-dimensional model.In this study,ANSYS Fluent is again used.The convection terms are modeled with a second-order upwind scheme.The fluid(R245fa)is assumed to be viscous and the turbulence closure is conducted by the realizable kepsilon model with the enhanced near-wall treatment.The rotor and the stator are connected by the mixing-plane interface,thus only one pitch of each of the rotor and the nozzle passages is modeled with a periodic boundary condition.The passage is discretized with hexahedral cells and the number of cells is approximately 0.6 million in total.The total pressure,the total temperature and the flow angles are specified at the nozzle inlet while the back pressure is specified at the rotor exit.

3.2.2 Validation of Perfect Gas Model“PG2”

At first,PG2 was applied in the perfect gas CFD simulation and the results were compared with a corresponding real gas simulation.The real gas model applied in this comparison is again provided by NIST REFPROP.The post-processing outside of Fluent(calculations on an MS-EXCEL spread sheet,for example)was conducted using exactly the same gas model as used in each corresponding CFD simulation to strictly insure the consistency.

Figure 5 compares the overall turbine performance:the pressure ratio,the isentropic efficiency and the power output predicted with two different gas models.For the PG2 case,all these performance parameters are once non-dimensionalized and converted to the corresponding real gas condition by means of the method stated in the previous section.All the data are normalized by each design point value acquired in the real gas simulation.In all of these performance comparisons,there can be observed only a negligibly small difference between the two solutions.Especially in the vicinity of the best efficiency point(the design point),the agreement is very good.

Figure 6 displays Mach number contours obtained with PG2 and with RG,respectively.Fundamental flow patterns are quite similar to each other,but a difference in the relative Mach number level is apparent near the exit region of the rotor.PG2 predicts higher rotor exit Mach number than RG.

In order to quantitatively evaluate the deviation in Mach number,the isentropic Mach number was calculated.At first,for the rotor passage,the local relative total enthalpy is calculated using the conservation of rothalpy as

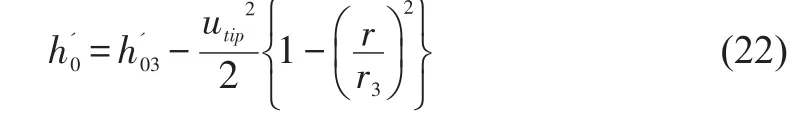
Then the isentropic enthalpy and the speed of sound corresponding to the local static pressure are evaluated asand,and the isentropic Mach number is calculated by

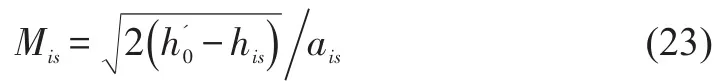
The isentropic Mach number in nozzle passage case can be calculated in a similar manner.

Figure7(a)displays the deviation in the isentropic Mach number on the nozzle vane surface at the mean section.As can be expected from the result of the previous de Laval nozzle study,no substantial deviation in the isentropic Mach number can be observed in this stationary nozzle passage.On the other hand,the Mach number deviation of the rotor blade surface is as high as 0.1,see in Figure 7(b).

In an attempt to examine the reason of this discrepancy,the isentropic density ratio is expressed in terms of relevant non-dimensional parameters as,

This expression suggests that the higher the isentropic exponent,the lower the exit density,and similarly,the higher the parameter,the lower the exit density.This latter parameter is related to the stage pressure ratio.Generally speaking,a higher pressure ratio stage,which has an inlet condition closer to the critical point and has a larger difference between the real isentropic exponent value and the numerically stable one,tends to have a lower predicted exit density.The adopted value ofγin PG2 is the highest one in the actual turbine passage,thus PG2 should predict an excessively low exit density.The deviation in Mach number is considered to be mainly caused by this excessive decrease of the density,which results in the higher through-flow velocity.

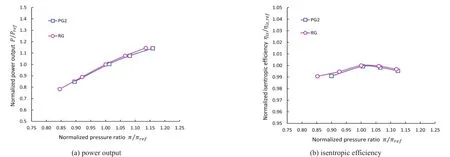
Fig.5 Overall turbine performance(total-total)

Fig.6 Mach number at mean section(relative Mach number in rotor,absolute Mach number in nozzle)

3.2.3 Validation of Perfect Gas Model“PG2S”

Next PG2S was applied in the CFD simulation of the same turbine stage.Figure 8 compares the performance characteristics.In Figure 5,the pressure ratio and the efficiency are defined by total-total basis.But in order to emphasize the influence of the density on the performance as seen in the previous sub-section,they are now defined by total-static basis.

The efficiency discrepancy between RG and PG2 is about 1%,rather a big difference,and is supposed to be caused by the differences in the discharge velocity and density.By applying PG2S,the efficiency is predicted quite closely to RG.The output power is not affected appreciably,whether defined in total-total or total-static,and PG2S predicts it as accurately as PG2 does.

Figure 9 displays the Mach number difference between PG2S and RG.The deviation in the nozzle increased only slightly compared with PG2,but still negligibly small.On the other hand,the deviation in the rotor is greatly suppressed.This is a consequence easily expected from Table 1.On the other hand,no appreciable deviation can be observed in the leading edge part of the rotor,implying that PG2S can more accurately predict the rotor inlet flow vector.The gradual increase of the deviation toward the trailing edge observed in PG2 is also disappeared.

3.2.4 Improvement of“PG2S”

A further improvement of PG2S was attempted using Equations(16)-(19).Hereafter,we call this model as“PGS”.In this model,the non-dimensional parameters and the real gas parameters are defined based on any isentropic condition.Therefore it is applicable even whenγis lower than unity still at the turbine exit,by adopting a sufficiently lower reference pressure of arbitrary selection.PG2S is a special case of PGS,in which the turbine exit static pressure is used to define the isentropic condition for the modelling.

In order to evaluate the effectiveness of this modification,Mach number deviations by several PGS models(severalγvalues),including PG2S,are compared in Figure 10.Here,notice that the vertical axis is more exaggerated than Figures 7 and 9 in order to clearly display the difference among the models.Generally,the deviation levels are similar to each other,confirming that PGS is as accurate as PG2S,but the deviation is apparently smaller for the lowerγbecause it is a better representative of the turbine internal thermodynamic behaviour.Aγvalue higher than PG2S corresponds to an isentropic condition the pressure of which is lower than that of the turbine exit,thus inevitably less accurate.But such a modelling may be indispensable when the turbine back pressure is still close to the critical value and the correspondingγvalue is close to or even lower than unity.

Finally all three perfect gas models,PG2,PG2S and a series of PGS's,are compared in terms of deviations in turbine exit flow parameters,the Mach number and the swirl angle,in Figure 11.It is obvious that PG2S is much more accurate than PG2 and PGS's can further improve the accuracy.All PGS models including PG2S are satisfactorily accurate for the aerodynamic design purpose,though the smallerγvalues give slightly better accuracy.But aγvalue excessively close to unity may cause a slow CFD convergence or even an unacceptably high residual due to the intrinsic instability even ifγis higher than unity.

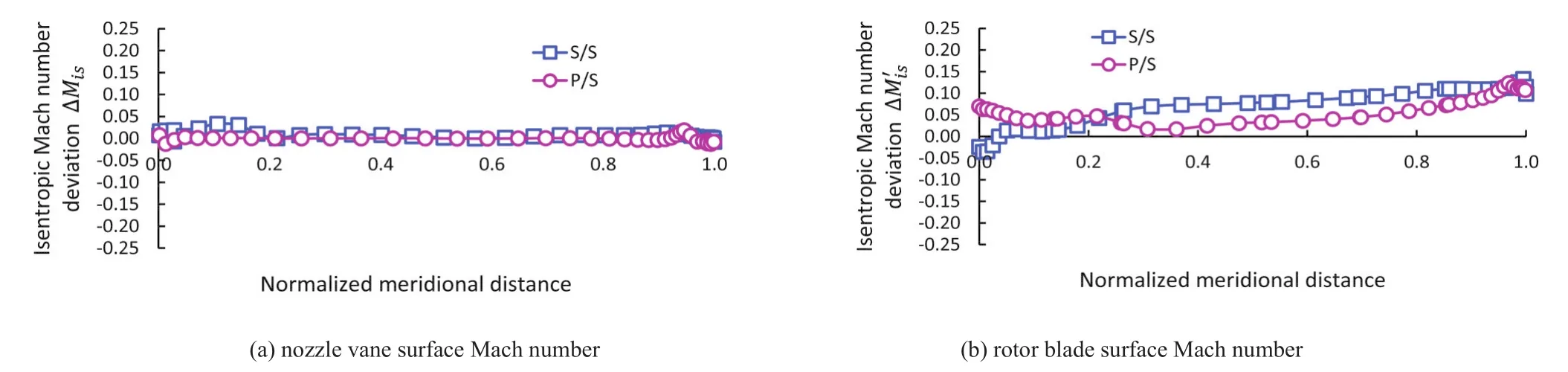
Fig.7 Deviations in blade/vane surface isentropic Mach numbers(PG2)

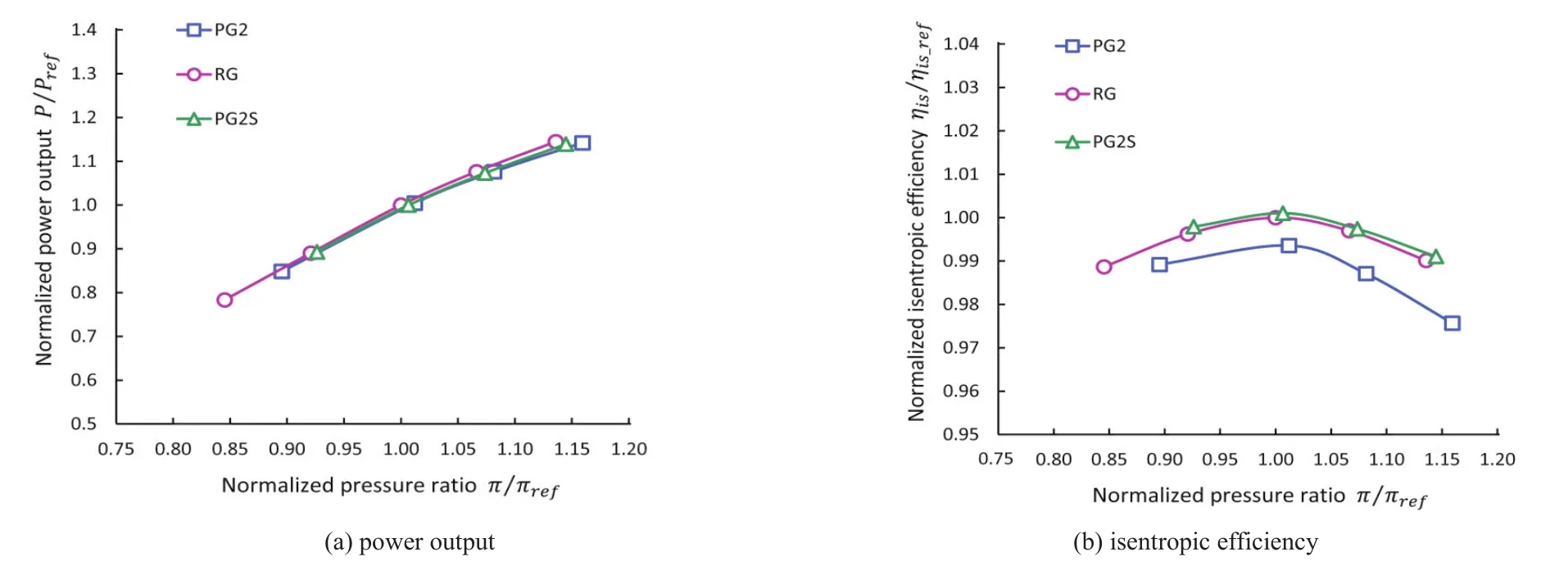
Fig.8 Overall turbine performance(total-static)

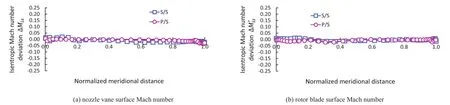
Fig.9 Deviations in blade/vane surface isentropic Mach numbers(PG2S)

Fig.10 Deviations in blade/vane surface isentropic Mach numbers(PGS)

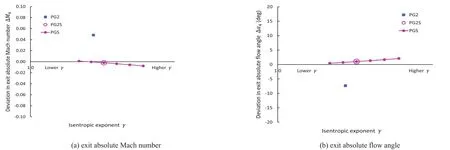
Fig.11 Deviations in turbine exit flow parameters

4 Conclusions

An accurate and reliable method of the perfect gas approximation for R245fa was developed which can be successfully applied in the aerodesign of the ORC turbine.The accuracy of the perfect gas approximation and the validity of the performance conversion method between the different gas models through the suitably defined non-dimensional performance parameters were demonstrated.The deviations in the performance parameters and in the internal Mach number were suppressed to negligible levels.The proposed perfect gas model can accelerate the design simulation of the ORC turbine without spoiling the accuracy and the stability.