实际安装状态下的盘式拉杆转子模态测试分析*

（华北电力大学电站设备状态监测与控制教育部重点实验室）

0 引言

近年来，燃气发电作为一种清洁发电技术受到普遍关注。与常规的蒸汽发电机组相比，燃气发电机组结构及工作条件具有特殊性，燃气轮机转子多采用盘式拉杆组合式结构，具有质量轻、强度大、便于加工以及易于装配等优点。但是盘式拉杆转子的拉杆持续在高温状态下运行将产生蠕变松弛，使得转子整体性下降，当拉杆松弛到一定程度，转子盘间接触面的刚度下降，转子在旋转过程中会产生类似裂纹一样的效果，如果不能及时发现这种现象，任由拉杆蠕变松弛状况发展，可能发生严重的转子解体事故，造成严重的设备损失，因此拉杆转子动力学特性的研究成为近年来的热点。目前国内外在该领域的研究主要集中在拉杆转子非线性动力学特性的数值模拟研究，有关研究现状的论述见文献[1]。在实验研究方面，国内外学者都进行过相关的工作。文献[2-6]对拉杆转子进行了模态测试实验，测得了转子的固有频率；文献[7-8]中对拉杆转子试验台上的拉杆转子进行了动态特性测试。上述试验测试中的拉杆转子都是处于自由状态。而在实际状态下转子由轴承支撑，两端连接启动设备和发电设备，与自由状态的边界条件差别很大，转子的固有特性必然会受到影响。因此，探究实际安装状态下拉杆转子的固有特性具有实际意义。基于此，本文对多盘拉杆式转子结构在两端安装电机和未安装电机两种状态下的动态特性进行实测分析，以“电站设备状态监测与控制”教育部重点实验室搭建的多盘拉杆转子实验台为对象进行实验模态分析，研究转子边界条件变化对拉杆转子模态参数的影响。

1 模态测试原理

对于多自由度系统，其在任意激励下的基本振动方程为：

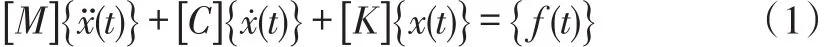
其中，[M]为质量矩阵，[K]为刚度矩阵，[C]为阻尼矩阵，{x（t）}为位移矢量，{f（t）}为激励力矢量。

对方程（1）进行拉氏变换，可得：

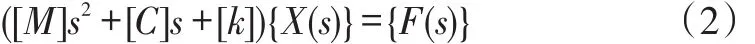
则系统的传递函数为

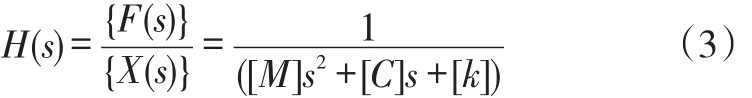
若令s=jω，得到系统的频响函数：

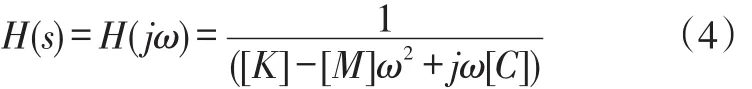
若激励信号为{F（t）}，响应信号为{X（t）}，通过以上变换可以得到系统的传递函数矩阵

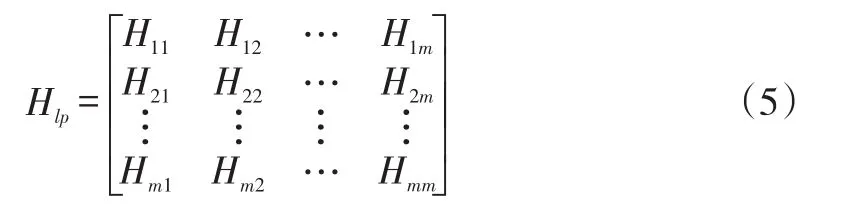
传递函数矩阵中每个元素Hij对应激励点i和响应点j之间的传递函数，其中包含有对象的固有特性信息；而传递函数矩阵中的任一行或任一列元素中还包含了对象的振型信息。试验模态分析就是给对象施加激励，测取激励和响应信号，计算传递函数，通过模态参数识别方法得到对象的模态参数。为了得到对象的振型，需要测取式（5）传递矩阵中的一行或一列元素，相应地可以采用多点激励、单点响应的方法，或者单点激励、多点响应的方法。对被测对象施加激励的主要方法之一是锤击法[9-15]，使用力锤敲击被测结构，通过测量力锤的激励信号和响应点的响应信号，对信号做傅里叶变换可以获取两点之间的传递函数。通过锤击法将结构上各测点之间的传递函数全部获取，便可得到整个结构传递函数矩阵中的一行或一列元素。从传递函数中，可以提取出系统的模态参数（模态频率和模态振型）。模态参数识别方法主要分为时域法和频域法两类。时域法即从时域响应数据中获取模态参数。频域法又称传递函数法，即在频响函数的基础上，利用最小二乘法以获取模态参数，得到系统的固有特性。

2 实验对象试验装置

“电站设备状态监测与控制”教育部重点实验室搭建的多盘拉杆转子实验台结构如图1所示。该实验转子为某型燃气轮机拉杆转子的简化模型，转子部分长度约为2m，分为两个带有叶轮的转子，中间通过刚性联轴器连接。图中左侧转子由5个轮盘组成，用于模拟压气机转子，右侧转子由3个轮盘组成，用于模拟透平转子。两部分轮盘均由6根周向拉杆拉紧。整个转子一端由交流电机驱动，另一端带发电机作为转子负载，可以实现并网发电。

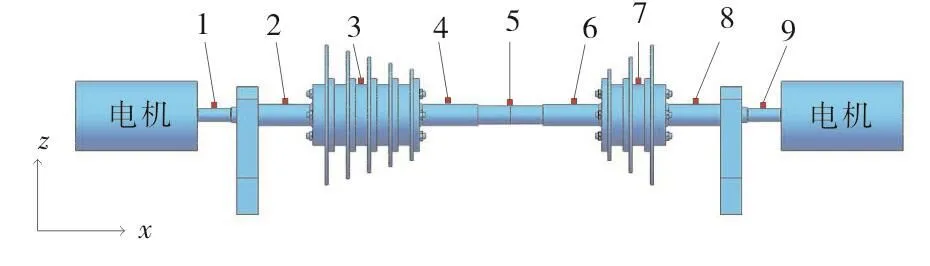
图1 测点布置图Fig.1 Measuring point layout

采用锤击法对转子结构进行模态分析，模态实验采用单点激励、多点响应方法，用力锤沿竖直方向进行敲击，由加速度传感器采集各测点Z方向的响应信号。考虑转子的结构特点，沿转子轴向设置9个测点，测点布置图如图1所示，力锤激励点为2点。试验所用模态测试和信号分析软件为SmartOffice V4.4，信号采集前端为m+p vibRunner 16通道LXI总线，模态测试分析仪采样频率为512Hz，频率分辨率为0.5Hz。模态测试系统分析图如图2所示。

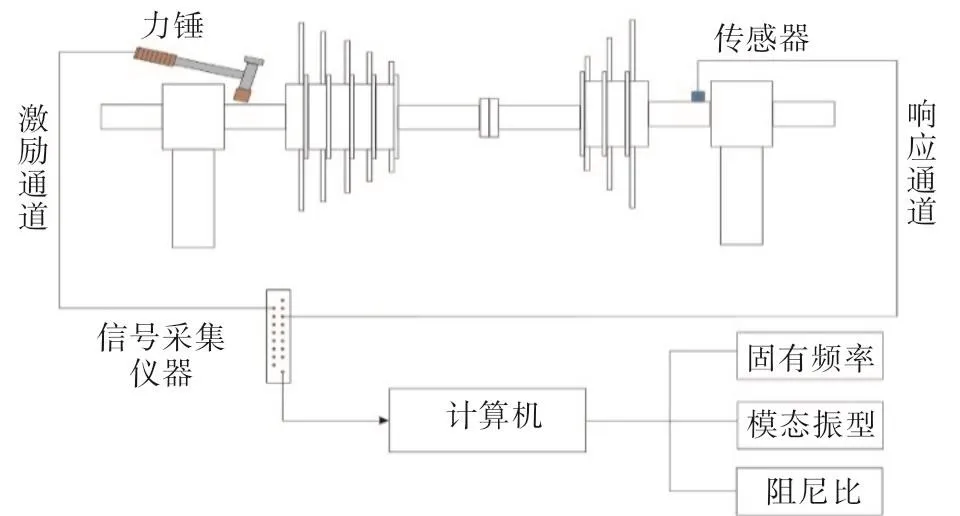
图2 模态测试系统分析图Fig.2 Modal test system analysis diagram

试验中转子采用原装支撑的方式进行模态测试，即转子由轴承支撑，固定在实验平台上。试验分两部分进行，首先进行连接电机状态下的模态测试，之后将电机拆卸，进行无电机连接状态下的模态测试。

3 试验结果及分析

分别对转子带电机和不带电机两种状态下的结构模态进行测试分析。每种状态下进行多次锤击测试，取相干函数较好的数据进行模态参数识别。图3示两种状态下的测试数据相干函数图。从图中可以看出两种状态下的相干函数值均在0.8以上，说明激励信号和响应信号的相干性好，试验数据可信度高。

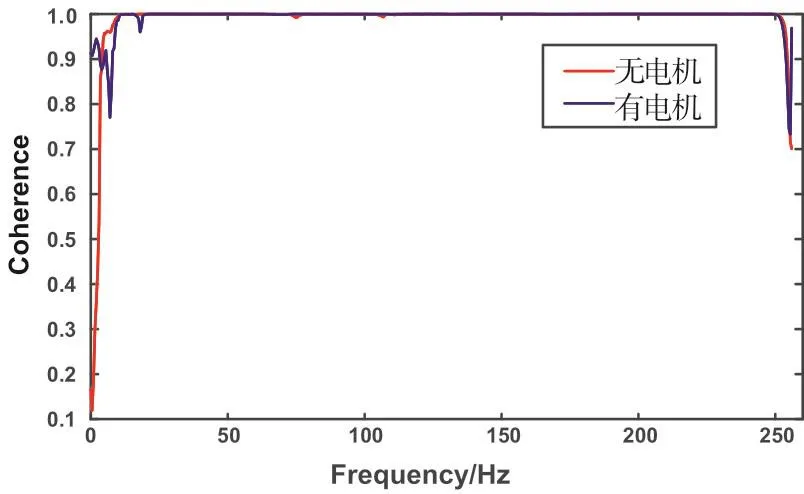
图3 两种状态下的相干函数Fig.3 Coherence function in two states

图4示出两种状态下的转子结构上第7测点的频响函数曲线，其中红色曲线为未安装电机时的频响函数，蓝色曲线为安装有电机时的频响函数。频响函数的峰值处的频率值即为转子的固有频率。从图中可以看出，安装有电机时的频响函数的曲线相对于未安装电机有整体向右偏移的现象。其中曲线的第一、第三个峰值向右偏移，即转子的第一、第三阶固有频率增大。曲线的第二个峰值保持在原来的位置，未发生改变，即转子的第二阶固有频率未发生变化。

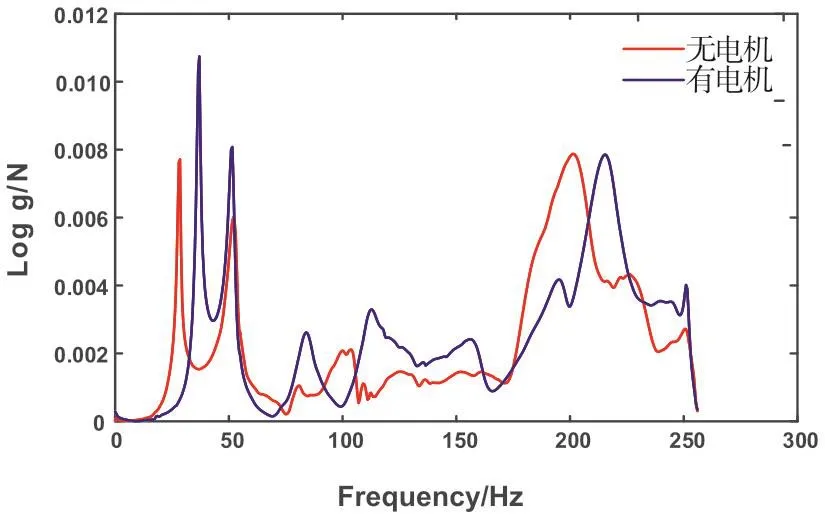
图4 两种状态下的频响函数Fig.4 Frequency response function in two states

在测试数据基础上，计算识别出转子的前三阶固有频率及其振型。固有频率如表1所示，从表中可以看出，安装电机时的转子第一、三阶固有频率要高于未安装电机时的固有频率，而第二阶固有频率相差不大，仅为0.64Hz。可以看出，安装电机后转子的固有频率从整体上有增大的趋势，意味着电机改变了转子的支撑状态，增大了转子的支撑刚度，从而改变了转子的固有特性。因此，边界条件对转子的固有特性有明显的影响，在实验时应当尽量做到原装支撑状态，模拟与工作环境接近的边界条件，以避免因实验边界条件和工作边界条件不同而带来的影响。

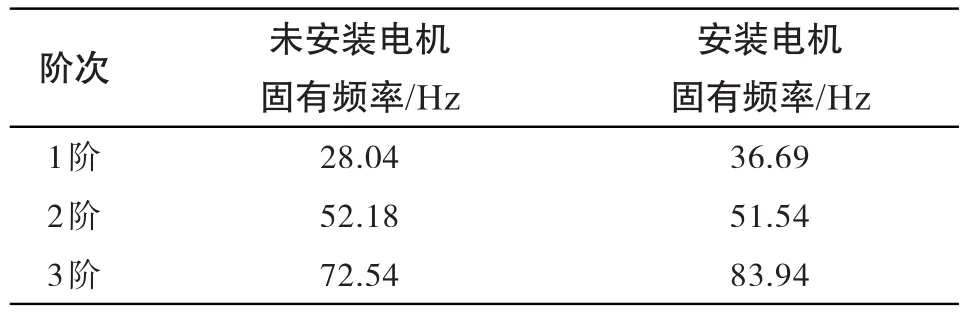
表1 拉杆转子固有频率Tab.1 Natural frequencies of the rod-fastening rotor

图5中所示为安装有电机时的转子结构前三阶模态振型，可以看出，盘式拉杆转子的振型符合一般转子横向振动的振型特征，第一阶振型的节点位于转子两侧固定端，第二阶振型的一个节点在转子中间联轴器附近，第三阶振型有两个节点，分别在转子上3-4测点和7-8测点之间。

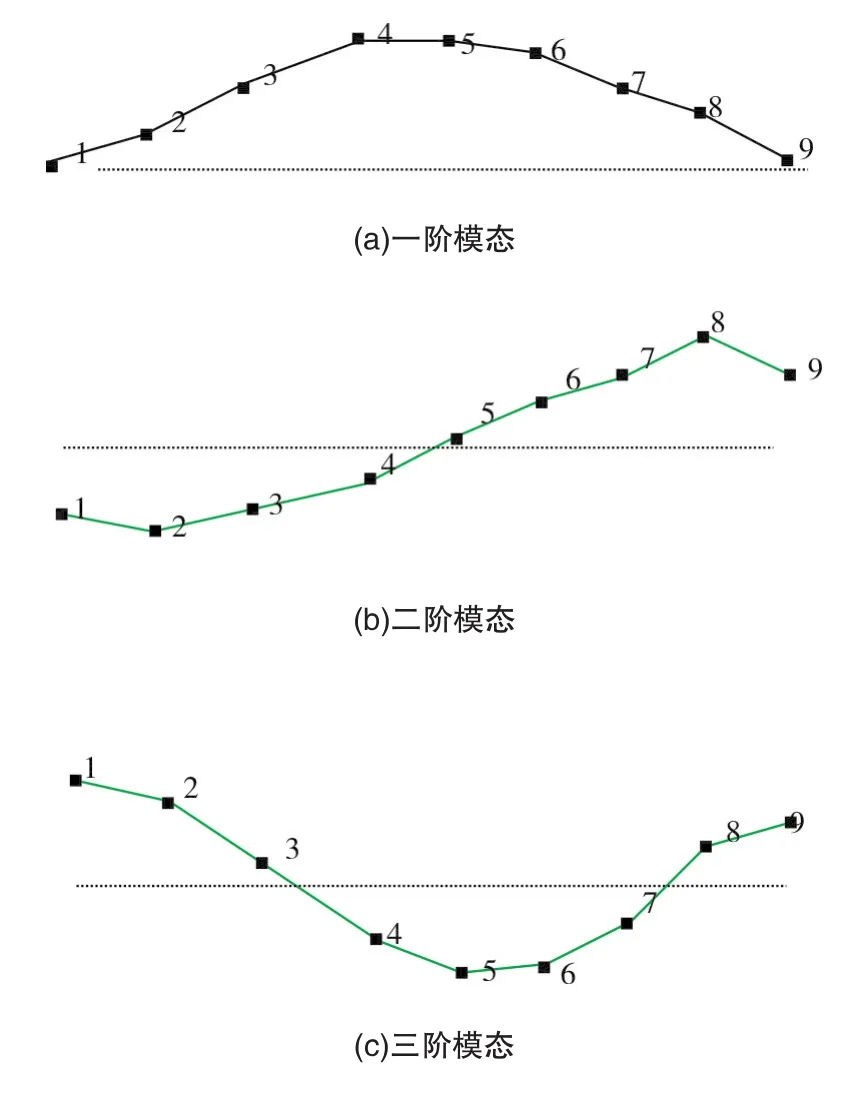
图5 安装有电机时的拉杆转子模态振型Fig.5 The mode shapes of the rod-fastening rotor with motor installed

4 结论

用锤击法测得了某型燃气轮机拉杆转子约化模型在安装电机和未安装电机两种状态下的固有频率和振型，其中未安装电机时的前三阶固有频率为28.04Hz、52.18Hz、72.54Hz，安装电机时的固有频率为 36.69Hz、51.54Hz、83.94Hz。振型为Z向的弯曲振动。

与未安装电机时相比，安装电机后转子的第一、三阶固有频率偏大，第二阶固有频率未发生明显变化。从频响函数曲线中可以看出，安装电机后转子的频响函数的峰值整体向右偏移，说明转子的固有频率整体增大，考虑为电机改变了转子的边界条件，从而影响了转子的固有特性。