仅天基测角跟踪的轨道机动WFMHT检测方法

刘磊, 曹建峰, 刘也

(1.北京航天飞行控制中心, 北京 100094; 2.航天飞行动力学技术重点实验室, 北京 100094)

空间态势感知技术利用对空间目标的测量信息确定其状态、属性和意图，是目前空间安全问题的主要应对和防范手段，其重要内容之一即对空间目标运动状态的实时精确估计和运动状态变化的快速准确检测。从空间目标的信息获取手段来看，天基观测由于不受地面光照、气象和地理条件等限制，近年来受到高度重视和广泛应用，如美国的天基空间监视系统(SBSS)和轨道深空成像系统(ODSI)，以及中段空间实验(MSX)卫星和天基红外预警系统(SBIRS)，其中SBSS使美国对地球静止轨道卫星的跟踪能力提高50%，MSX卫星能够探测7～15星等亮度的卫星和碎片，可同时探测地球低轨道和地球静止轨道卫星[1-3]，未来的空间目标信息获取或将发展到以天基观测为主，同时天基光学观测可能成为今后相当长时间内的主要天基观测手段[3]。在天基光学观测条件下，快速准确检测空间目标轨道机动引起的运动状态变化的难度较大。定性来看，空间目标轨道机动的检测结果很大程度上受观测能力和目标机动特性的制约，由于天基光学观测仅能获取空间目标的方位信息，并无距离和速度等信息，因此观测信息不完备，而且观测量往往较为稀疏。在这种有限观测条件下，常见机动检测方法的成功率往往较低。

目前，空间目标机动检测常见做法有3种，即噪声等价、输入检测与估计、模型切换。噪声等价方法将机动过程动力学建模为白噪声或者有效噪声，采用噪声补偿或者动力学模型补偿进行机动检测[4]。输入检测与估计将机动作为加速度输入进行检测和估计，多将目标机动检测表示为二元假设检验问题，检测方法包括常见的Chi2滑窗式显著性检验及其改进方法，研究内容包括输入序列假设、检测窗口长度选择、检验统计量构造等。如Ru等在大幅机动、小幅机动、CT机动、随机机动4种典型的机动场景下，通过ROC曲线等工具系统地比较了6种滑窗式机动检测器(Chi2-MR、Chi2-IE、Gauss-IE、GLRT、MLRT、滑窗式CUSUM)的性能，同时研究了窗口长度对检测性能的影响[5-7]。Ko等研究了利用推力傅里叶系数建模未知加速度，通过其变化检测轨道机动的方法，该方法无需预定义加速度模型，且适用于脉冲机动和连续小推力机动，还可以估计机动的起始和终止时刻[8-11]。Jaunzemis等研究了基于燃料最省控制距离度量的轨道异常假设检验方法，融合了非高斯边界条件不确定度，并采用二元假设检验以包含检测门限和允许误差率，结果表明对于非高斯边界条件，控制距离方法的检测性能和计算复杂度优于Mahalanobis距离[12-13]。Lubey等研究了用于轨道机动检测和重构的最优控制融合估值算法，采用观测值残差进行机动检测，不过仍然存在检测可靠性和小幅值轨道机动漏检等问题[14-15]。Goff等研究了非合作目标机动重建的参数需求[16]。Lan等将轨道机动建模为带未知扰动输入的非线性随机系统，用迭代最小上界滤波器通过迭代优化来降低估计误差的协方差上界，通过最优衰减因子与经验门限值比较来确定轨道机动[17]。模型切换方法建立包括轨道机动的多个运动子模型，在滤波过程中通过相应策略选择估计模型，典型如常见的交互多模(IMM)及其改进方法。Jia等提出了一种IMM求积卡尔曼滤波器，用于空间目标的天基测角跟踪和机动检测，其中使用了4个天基光学设备进行天基测量[18]。Goff研究了非合作机动目标轨道估计，采用IMM估计瞬时机动轨道[19]。模型切换方法的性能取决于子模型精度和相应切换策略，且严重依赖于轨道机动检测结果。

因此，空间目标机动检测研究一方面多集中于导弹跟踪和制导等高动态系统，相应观测条件良好，并不适用于仅利用天基测角信息的外层空间目标轨道机动检测。另一方面，在天基观测信息类型单一、观测条件苛刻条件下，如何选择轨道机动检测量以及构建高效准确的检测结构，从而仅利用天基测角就可快速准确检测出非合作目标的未知轨道机动，值得深入研究。

为此，本文研究了仅天基测角跟踪的空间目标轨道机动检测方法，建立天基测角跟踪的空间目标运动状态实时估计模型，选择实时估计的测角新息作为机动检测量，基于随机序列的假设检验方法构建空间目标轨道机动的加权融合检测结构，以此降低检测窗口长度和虚警概率，提高空间目标轨道机动检测的快速性和准确性，同时增强机动检测器的鲁棒性能。

1 天基测角跟踪

基于天基测角的空间目标跟踪如图1所示[3,20]，其中S为天基观测平台,T为空间目标。设T和S的地心矢量分别为r和R,二者距离为ρ,于是有

r=R+ρL

(1)

式中,L为S至T的单位方向矢量,设天基角度测量数据为赤经α和赤纬β,易得L

(2)

图1 空间目标的天基测角跟踪

基于天基测角对空间目标的实时跟踪问题,即通过角度测量信息借助状态估计算法,求解空间目标的实时状态。设空间目标的状态量X包含位置和速度,即

(3)

借助轨道动力学,可以得到离散的状态方程

(4)

至于测量方程,可以直接取天基观测平台得到的相对角度作为观测量Y,由(2)式得

(5)

将天基观测几何关系式(1)与(5)式结合可以给出线性化测量方程

y=ΔY=H·ΔX+V

(6)

式中,V为观测误差,设其为零均值白噪声,有E[V(k)VT(j)]=R(k)δ(k-j)。H为观测量对状态量的偏导数阵,即

(7)

(8)

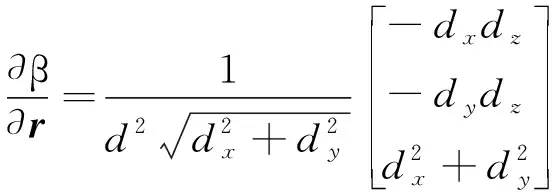
(9)

d=r-R

(10)

利用状态方程(4)和测量方程(6),采用经典的扩展卡尔曼滤波(EKF)方法,可以实现基于天基测角的空间目标运动状态估计,即对空间目标的实时跟踪。

对于非线性连续系统

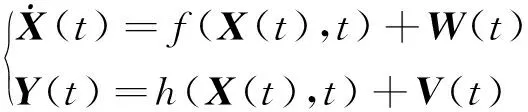
(11)

EKF滤波公式[4]为

式中

由上述模型可见,在观测平台轨道已知条件下,仅利用单星光学测角信息,无法实现对非合作空间目标的单点定位和定轨,因此为了实现对非合作空间目标的实时跟踪滤波,必须首先解决天基测角条件下的初轨确定问题,文献[3]对该问题进行了较为充分的研究,可为本文研究提供可靠的初始轨道。

2 轨道机动检测

仅利用天基测角实现对空间目标轨道机动的快速精确检测,依赖于以下几方面问题的解决,即检测量的选择、假设检验方法、检测器结构方式以及相应参数的确定等。

2.1 检测量选择

检测量的选择需充分考虑其对运动状态变化的反映速度和程度,从而直接决定空间目标轨道机动检测的准确性。在空间目标的运动状态估计过程中,测量新息作为状态估计方法的重要参数,可以较为准确地反映状态估计的精度,充分体现运动状态的实时变化,因此,在目前对飞行器运动跟踪研究中,经常采用状态估计中的测量新息作为状态变化的检测量。

由EKF数学模型可知,各次状态估计的新息υk为

(17)

可以证明,线性最优滤波的新息序列{υk}是零均值白噪声[22],即

(18)

当空间目标发生轨道机动时,其运动状态将会发生变化,此时,新息序列就不再为零均值白噪声。反之,当检测到空间目标运动状态估计的测量新息序列不再呈现白噪声特性,在天基观测平台运动已知,并且假定测量可靠的条件下,由此判断空间目标运动状态产生了变化,即产生了轨道机动。

检测量确定后,可以选择单个或多个数据点进行假设检验,即单点检测和滑窗检测,前者实时性最好,但是检测结果的可靠性和准确性不如后者。下文将采用滑窗检测,且分析窗口选择对检测结果的影响。

2.2 假设检验方法

假设检验方法在假设样本总体满足某个特定分布的条件下,构造检验统计量,然后取一定显著性水平,利用该统计量的分布特性确定拒绝域,进行假设检验。对于总体分布类型未知的采样,可以根据样本来检验关于总体分布的假设,即分布拟合检验[22]。本文采用如下分布拟合检验方法:χ2检验法、SK法(偏度峰度检验法)、JB(Jarque-Bera)法、KS(Kolmogorov-Smirnov)法与LF(Lilliefors)法[23-25]。

在总体的分布未知时,χ2检验法根据样本xi(i=1,2,…,n)检验总体分布的以下假设:

H0:总体x的分布函数为F(x)

H1:总体x的分布函数不是F(x)

χ2检验法的检验关系式为

(19)

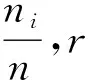
(20)

式中,g1和g2分别为样本的偏度和峰度,也即三阶和四阶中心矩的矩估计

(21)

KS法将总体分布与标准正态分布对比进行检验[23],其检验统计量为

xKS=max(‖F(x)-G(x)‖)

(22)

式中,F(x)和G(x)分别为经验累积分布函数和标准正态累积分布函数。

LF法改进KS法结果易受分布函数影响的缺陷[24],构造如下检验统计量

xLF=max(‖F1(x)-F2(x)‖)

(23)

式中,F1(x)为由样本估计出的经验累积分布函数,F2(x)为均值和标准差与样本相等的正态累积分布函数。

2.3 加权融合检测

(24)

则γk满足自由度为υk维数(设为m)的χ2分布,即γk～χ2(m)。对于仅天基测角跟踪的空间目标机动检测而言,m=2。

上述检测方法简单易于实现,不过由于仅利用单个假设检验方法,检测结果的准确性完全受制于该检验方法的性能,尤其是造成检测器结构单一,可靠性和鲁棒性较差。

为此,这里借鉴信息融合思想,提出一种对测量新息检测结果融合的方法,即利用上述几种假设检验方法分别进行检验,然后对各个检验结果融合作为最终的机动检测结果,相应的检测器结构如图2所示。

图2 空间目标轨道机动的多假设检验融合检测

由图2可见,对多种假设检验结果进行融合的检测结构,可以充分利用各种假设检验方法的优点,从而避免单一方法造成的误检和漏检,提高了检测结果的正确性和降低检测所需时间,而且多检测并行融合有利于增强系统的可靠性和鲁棒性,大大降低了检测器的失效概率。

图2中融合检测结构的关键在于对各个检测结果的融合方式,综合融合效果和计算量考虑,这里采用线性加权方式融合各个检测结果。设当前时刻的新息为υk,取滑动窗口长度为n的采样{υi}(i=k-n+1,k-n+2,…,k),在显著性水平α下,利用{υi}检验新息总体υ是否满足正态分布,设各方法的假设检验结果为

(25)

则线性加权检测融合结果νwf为

(26)

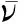
(27)

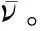
可见,本文方法基于对空间目标运动状态的精确实时估计,通过对测角新息的变化进行加权融合检测以判断目标机动与否,因此,对空间目标运动的精准实时跟踪是机动检测的重要前提。在(4)式和(6)式组成的天基测角跟踪系统中,观测量维度小于状态量,系统不可观,虽然在仿真中即使给定比较恶劣的跟踪条件,均未出现滤波发散问题。但是,在实际任务中,仍然需要充分考虑初值偏差过大、测量精度过低甚至测量中断等异常情况引起的滤波收敛性问题,以确保用于机动检测的空间目标运动实时跟踪新息的正确性。

3 数值仿真

数值仿真验证上述基于新息的多假设检验加权融合检测方法的有效性,同时由于待检验的新息序列长度即检测窗口长度,以及轨道机动量大小等,均直接影响空间目标轨道机动检测结果,故选取不同轨道机动量和窗口长度,给出对应的检测结果,并与常见χ2检验方法进行对比。

仿真中,天基观测平台为高度1 600 km的圆轨道,倾角54°,考虑2个高度不同的空间目标,其中高轨空间目标为高度20 000 km的圆轨道,倾角30°,升交点赤经0°,真近点角40°,低轨空间目标为高度300 km的圆轨道,倾角45°,升交点赤经358.8°,真近点角345.2°。天基观测平台与2个空间目标之间均存在长达1 h的可见弧段,基于目前的天基光学载荷性能,观测间隔取1 s,观测误差为零均值白噪声,标准差为5″。设空间目标的初始位置和速度误差均为白噪声,标准差分别为50 km和50 cm/s。轨道机动假设发生在500 s时刻,机动量大小分别为1 m/s,5 m/s,10 m/s,20 m/s,50 m/s和100 m/s,检测窗口长度n分别选择30 s,60 s,90 s,120 s和180 s。各种假设检验的显著性水平均取0.01。

在上述仿真前提下,若空间目标无轨道机动,用2.2小节各种假设检验方法检验观测α和δ的新息序列,结果均满足与测量一致的正态分布,由此验证了仅天基测角跟踪空间目标的模型正确性。若空间目标发生了轨道机动,以高轨空间目标且轨道机动量5 m/s,机动时刻在500 s为例,α和β的新息序列如图3所示,新息序列明显不再符合正态分布特性。

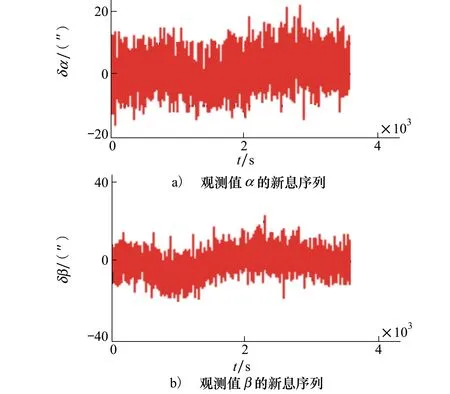
图3 空间目标轨道机动的观测新息

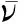
表1 仅天基测角跟踪的高轨空间目标机动检测结果 %

由表1可见,无论是常见χ2检测方法还是新息多假设检验加权融合检测方法,检测成功率均随着轨道机动增大和检测窗口增加而提高,其中,新息多假设检验加权融合检测方法除了对于1 m/s轨道机动的检测成功率在60%左右,对于5 m/s以上的轨道机动检测成功率全部大于78%,且绝大多数在90%以上。

表1中2种方法的对比结果如图4所示,Δη为新息多假设检验加权融合检测方法相对于常见χ2检测方法提高的成功率。

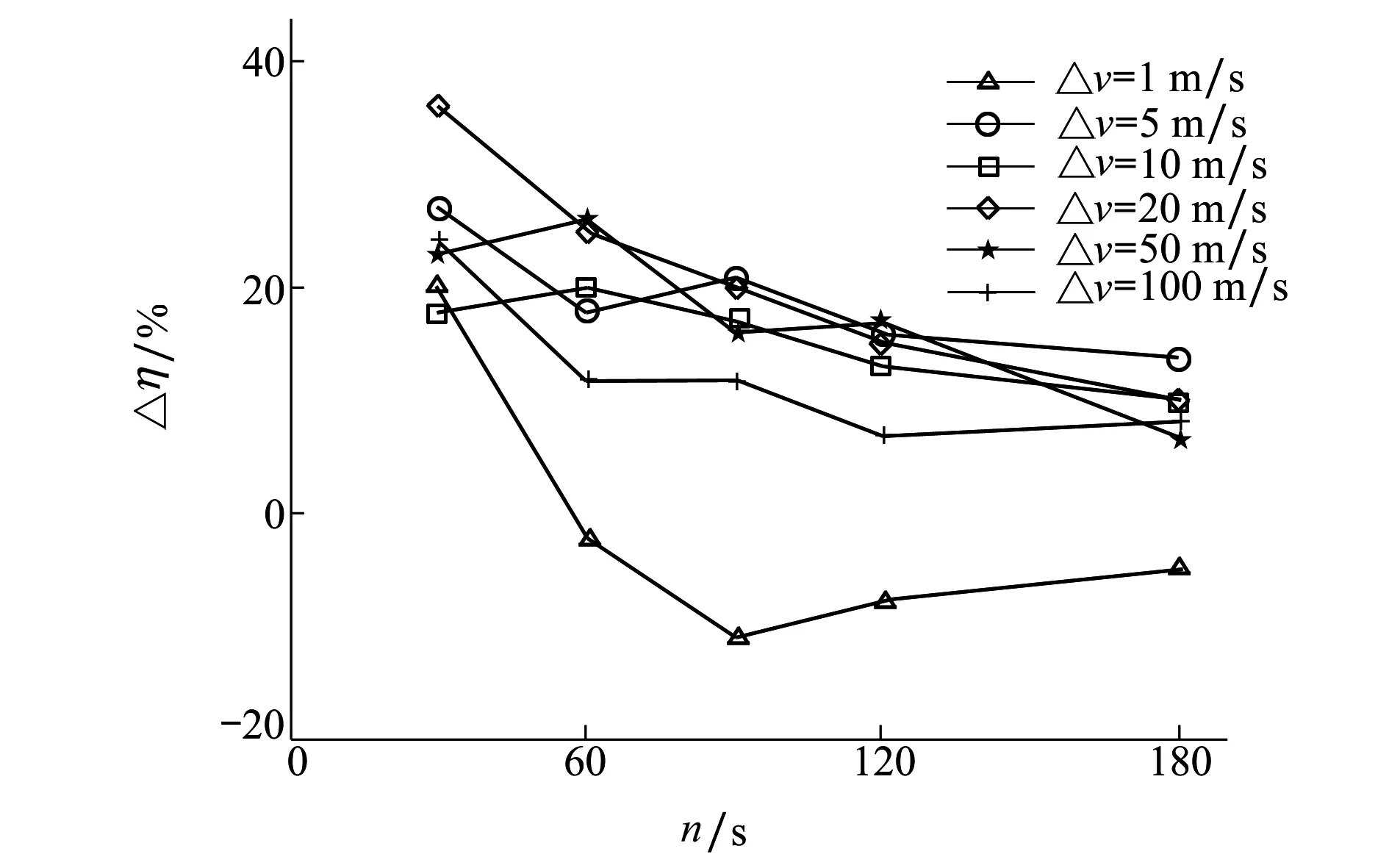
图4 新息多假设检验加权融合检测方法相对于χ2检测方法的改进(高轨空间目标)

由图4可见,相对于常见χ2检测方法,新息多假设检验加权融合检测方法的轨道机动检测成功率明显提高,尤其是在检测窗口较短时,改进效果更加明显。当检测窗口为30 s时,对于给出的6个大小不同的轨道机动,采用新息多假设检验加权融合检测方法的轨道机动检测成功率提高18%～36%。当检测窗口为60 s或90 s时,除1 m/s轨道机动结果大致相当,其它轨道机动的检测成功率均提高12%～26%。当检测窗口增加到120 s或180 s时,轨道机动检测成功率仍有明显提高,最大可以达到17%。

图5 新息多假设检验加权融合检测方法相对于χ2检测方法的改进(低轨空间目标)

由图5可见,对于低轨道空间目标,新息多假设检验加权融合检测方法相对于常见χ2检测方法的检测成功率也有明显提高。当检测窗口为30 s时,对于给出的6个轨道机动,采用新息多假设检验加权融合检测方法的检测成功率提高5%～18%。当检测窗口为60 s或90 s时,轨道机动的检测成功率均提高7%～29%。当检测窗口增加到120 s或180 s时,轨道机动检测成功率提高约9%～26%。与前述高轨道空间目标相比,对量级较小的轨道机动的检测成功率提高明显。

需要说明,低轨道空间目标的轨道机动检测使用与高轨道空间目标相同的融合检测加权系数和检测判断阈值,充分验证了利用上述方法得到的参数的适应性。事实上,如果在低轨道空间目标的轨道机动检测中重新计算融合检测加权系数和检测判断阈值,新息多假设检验加权融合检测方法的检测效果更好,相对于常见χ2检测方法的检测成功率会提高30%以上。此外,还仿真了不同观测精度条件下的轨道机动检测,结果均表明基于测量新息多假设检验加权融合检测的机动检测方法优于常见χ2检测方法。

4 结 论

面向空间态势感知中的空间目标轨道机动检测需求,研究了仅利用天基测角的空间目标轨道机动检测,提出了基于测量新息多假设检验加权融合检测的轨道机动检测方法,并采用数值方法与常见χ2检测方法进行了对比。研究结果表明,基于测量新息多假设检验加权融合检测的机动检测方法,充分利用了多种假设检验方法的优点,可以大大提高空间目标轨道机动检测的成功率,相对于常见χ2检测方法的成功率可以提高36%,尤其改善了短检测窗口的检测结果。同时,本文方法通过对多种检测方法的融合,改变了仅利用χ2检测方法的单一检测结构,提高了系统的冗余性和鲁棒性,可为我国空间态势感知体系建设提供有益借鉴。