基于横向供应与维修比例的民机备件配置优化技术研究
2019-01-03冯蕴雯刘雨昌薛小锋路成
冯蕴雯, 刘雨昌, 薛小锋, 路成
(西北工业大学 航空学院, 陕西 西安 710072)
备件是飞机维修保障的物质基础,合理的备件供应保障策略对飞机持续安全运营有着重要的影响。备件库存不足将会影响飞机的飞行可靠性与签派可靠度,库存过多又会带来高昂的库存保管费用,因此开展备件的库存优化配置研究有着重要的实际意义。在民用航空领域,传统的维修保障模式是由航站直接向基地申请备件补给,没有考虑航站之间发生横向供应。而在实际工程中,某一航站发生备件短缺,为了保障飞机的正常运营,直接从相邻航站进行备件补给这种情况会经常发生,这种情况被称为横向供应模式,并且横向供应模式会比传统保障模式节约更多的时间与成本。但在目前横向供应问题的研究中,尚没有考虑维修比例(即维修站点中能够修复的故障件数量占送修此站点的故障件总数的比例)这一实际因素的影响。在实际中,若故障件在基地不能被修复则会进行报废处理,并购置新的备件,因此若不全面考虑维修比例这一因素的影响将使库存配置结果与实际需求存在差异。为解决这一问题本文开展考虑横向供应及维修比例的备件多级库存配置方法研究以确定更经济、有效的库存配置方案,为民机备件的多级库存优化配置提供指导。
国内外学者对备件多级库存配置问题进行了较多研究,并且取得了一定成果。如Sherbrooke考虑维修保障组织的多级结构,提出了METRIC(multi-echelon technique for recoverable item control)理论用于多级库存配置研究[1];孙蕾等建立了基于METRIC理论的多级库存优化模型,并运用边际分析法对民用飞机关键部件的库存进行优化[2];Wayne等以美国空军保障模式为背景对多级保障组织的优化配置模型进行了研究[3]。以上研究虽然在多级库存配置模型中涉及了维修比例这一因素,但仅考虑了航站的维修比例,而基地仍具有无限修理能力,没有将维修比例这一因素考虑到基地维修过程中,与实际工程不相符致使库存配置结果与实际需求存在差异。而Lee对单个备件建立了考虑横向供应的2级库存配置模型,并基于METRIC用近似估计的方法推导了备件需求可以直接满足、可以通过横向供应满足以及备件发生短缺的概率[4];Axsäter对相似的库存配置模型进行分析,着重考虑需求量建模的准确性,并利用生灭过程推导了在任一库存水平下的稳态概率[5];Wong等结合某航空公司运营数据,以系统可用度为约束对横向供应下的多级库存配置模型进行研究,以减少航空公司维修保障成本以及系统的备件延误时间[6];Jung等针对可修件的2级可修问题,以备件满足率为约束对横向供应下2级库存配置系统进行研究[7];刘任洋等在部队现有保障模式背景下,以装备可用度作为保障效能约束指标建立了考虑横向供应的3级库存配置模型,并利用边际分析法进行库存的优化配置[8]。上述研究对考虑横向供应影响下的库存配置问题进行了分析,论证了横向供应模式的有效性与经济性,但没有考虑维修比例这一实际因素的影响,使得库存配置结果与实际需求存在差异。此外,薛陶等考虑实际中存在报废率的情况,以最小化维修成本为目标构建了2级单层的K/N冷备份冗余系统可修件优化模型[9];冯蕴雯等结合准更新理论、排队论和VARI-METRIC模型提出了考虑不完全维修的民机可修件多级库存规划方法[10]。虽然上述工作针对备件的多级库存配置问题建立了不同的库存配置优化模型,但是在具体应用中仍然存在一些不足:① 文献[1-3]没有全面考虑维修比例这一因素,虽然引入航站的维修比例,但仍然认为基地具有无限的修理能力,没有考虑到基地存在维修比例会产生报废并需要重新购置备件的实际情况,使得模型的库存配置结果与实际不符;② 文献[4-8,11-14]针对横向供应模式下的备件多级库存优化配置进行研究,验证了横向供应模型的经济有效,但没有在模型中考虑维修比例这一实际因素的影响,使得库存配置结果与实际需求存在着差异。
为了解决上述问题,本文针对民机备件的多级库存配置问题,结合民机维修保障模式,提出了一种考虑维修比例及横向供应的备件多级库存配置研究方法。首先,在考虑横向供应库存配置模型中引入维修比例这一实际因素,建立备件多级库存配置模型,并以备件满足率与机队可用度为约束条件,以库存系统总成本为优化目标建立数学模型;其次,运用边际分析法对备件在多级维修保障模式下的库存配置进行优化;最后,结合某航空公司运营数据,以波音737客机典型部附件作为研究对象进行实例验证,并与传统库存配置模型以及只考虑维修比例的非横向供应库存配置模型进行对比,验证了本文模型的有效性与可行性。
1 问题描述与假设
目前,航空公司多采用2级的维修保障体系,即航线级与基地级。传统的备件维修保障模式是由航站直接向基地申请进行备件补给,但对民机系统而言,各航站间的距离相比离基地的距离会近得多,如果某一航站发生备件短缺,直接从相邻航站进行备件的补给,将会比传统保障模式节约更多的时间与成本,这种由同级之间航站进行备件补给的方式就是横向供应。此外,在民机的2级维修保障体系中,航站与基地都具有一定的维修比例,即故障件中能够被修复的数量占故障件总数的比例。但以往的研究中对这一因素的分析不够全面,虽然引入航站的维修比例,但都假设基地的修理能力为无限大。这种假设与实际情况不符,由于维修比例这一因素的存在,基地不能实现对故障件的完全修理,会存在着一定的报废量,这会对备件的多级库存配置产生影响。为此,本文针对民机备件的航线可更换单元(line replaceable units, LRU),开展考虑横向供应与维修比例的2级单层库存配置研究。
民机的库存配置系统由航线级仓库、相应的航站维修站点、基地仓库和相应的基地维修站点组成。民机库存配置系统如图1所示,基地仓库和相应的修理站点数量为m,航站仓库和相应的修理点数量为n,系统中LRU数量为p,且备件在航线级会发生横向供应。库存配置系统示意图如1所示。
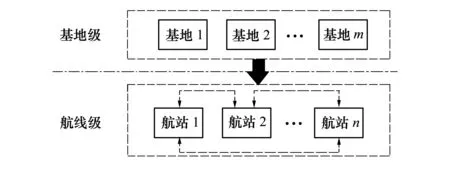
图1 横向供应模式下2级单层库存配置系统示意图
在多级修理模式下,通常按照航站与基地的距离,将航站划分为几个不同的共享组,且只在共享组内允许横向供应的发生,共享组内一般设有2个或3个航站。当飞机在某航站发生LRU故障时,如果该LRU在航站仓库有备件,则更换故障件,直接满足需求;如果航站仓库中没有备件,则向临近的航站提出横向供应申请,并由提供备件的航站向基地仓库提出补货申请;当共享组内的航站中都没有库存时,则认为出现短缺,此时向基地仓库申请备件补给,飞机停飞待件。拆换下来的故障件先在航站维修站点进行修理,航站有一定的维修比例,修理完成则送往航站仓库;若不能修理,则将故障件送往基地进行修理。基地也存在一定的维修能力,修理完成的备件送往基地仓库;若基地也不能修理,则将故障件报废,订购新的备件补充到基地仓库。当备件在后方基地修理完成后,若没有横向供应发生,则送回原航站;若存在横向供应情况,则送到有需求的航站仓库(横向供应中提供备件的航站)。考虑横向供应与维修比例的多级备件库存配置流程图如图2所示。

图2 考虑维修比例及横向供应的两级单层备件库存配置流程图
在上述的2级单层的横向供应库存配置过程中,仓库对LRU采用减少1件补充1件的(S-1,S)库存补货策略,并且满足经典库存平衡公式[2]:
s=sOH+sDI-sBO
(1)
式中,s为仓库的初始库存量,且s为一定值始终不变;sOH为某一时刻仓库的库存量;sDI为某一时刻仓库的供应渠道数,即正在维修的LRU数量以及在运输途中的LRU数量;sBO为某一时刻仓库LRU的短缺数量。当有LRU故障件进行维修时,sDI将增加1个,若仓库有库存,则sOH减少1个,否则sBO增加1个;当故障件维修完成时,sDI减少1个,sOH增加1个或者sBO减少1个。
为了简化建模过程以及提高模型的工程适用性,可以对备件库存优化模型合理地做出如下假设:
1) 所有LRU均为可修件,且LRU的故障服从泊松分布,不同故障件的维修时间相互独立;
2) 认为飞机型号均相同,且LRU的重要程度相同,一旦发生短缺将导致飞机停飞;
3) 每个航站的库存控制采用(S-1,S)库存补货策略;
4) 航线级的备件可以实现共享,当某航站发生需求且没有库存时,允许在共享组内通过横向转运从其他航站获得所需备件,但不可以跨组进行;
5) 组内存在2个以上的库存点时,需要明确转运点的选择原则,即先向距离近的航站申请,只有在近距离的航站没有存货时,才向稍远距离的航站申请;
6) 发生横向供应时,可以立马从相邻航站获得备件,不考虑延误时间;
7) 认为基地级与航线级,以及航线级不同航站之间的运输过程中,无故障发生。
2 考虑横向供应的2级备件库存模型
2.1 基地与航站的年平均需求量与供应渠道数
航空公司的飞机在运营过程中LRU的故障随时都有可能发生,某LRU的年平均需求量等于其1年内的平均更换量。每项LRU的年平均需求量可根据(2)式得到
(2)
式中,λi为每项LRU的年平均需求量,F为飞机年飞行时间,Qi为每项LRU的单机安装数量,N为机队规模,Mi为每项LRU的平均拆换间隔时间(MTBUR)。
飞机在一条航线上可能会经过多个航站,所以航站对某LRU的需求量可以根据航程计算得到。航站j中每项LRU的正常年平均需求量为
(3)

航站与基地都具有一定的维修比例,在航站修理不了的故障件将送往基地进行修理。所以基地某LRU的年平均需求量为所有在基地修理完成的LRU故障件之和。基地中每项LRU的年平均需求量为
(4)
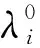

(5)
根据模型假设LRU的失效服从独立的泊松分布,由Palm定理可得,基地中每项LRU的供应渠道数为
(6)

由报废产生的供应渠道数为
(7)


(8)

由Palm定理,航站中每项LRU的供应渠道数为
(9)
2.2 横向供应下航线的需求量


(10)
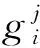
(11)
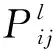
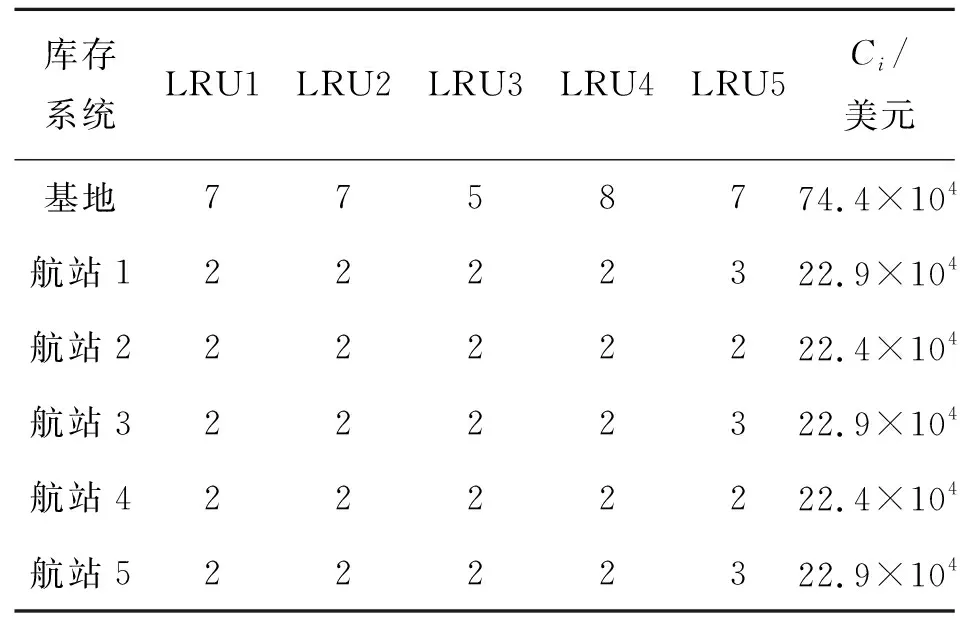
在共享组内,每一个航站的库存系统都可以看作是一个生灭过程[5]。建立航站的库存状态转移过程如图3所示。
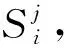

图3 航站库存状态转移过程图
可以得到在某一库存水平下的稳态概率为
(16)
由各库存水平下的稳态概率之和为1,可得
(17)
由此可得到
(18)
2.3 基地与航线的期望短缺量
基地中每项LRU的期望短缺数计算公式为
(19)
基地中每项LRU由报废产生的期望短缺数为
(20)
航站中每项LRU的期望短缺数为
(21)
2.4 数学模型
研究民机库存优化配置模型的目的就是希望在满足机队可用度和备件满足率的前提下,使库存系统的总成本达到最低。因此建立以库存系统总成本为优化目标,以机队可用度和备件满足率为约束条件的2级横向供应库存配置优化模型
(22)

航站中每项LRU的机队可用度为[13]
(23)
航站中每项LRU的备件满足率为
(24)
3 考虑横向供应与维修比例的备件库存配置模型优化流程
本文库存配置模型的优化算法选用边际分析法。虽然边际分析法的求解精度没有遗传算法的精度高,但是边际分析法在求解民机备件库存配置这一类复杂系统问题上具有更高的效率,是一种国内外普遍采用的方法。

图4 边际分析法库存配置流程图
库存配置模型的优化流程为:
1) 首先根据公式(2)~(3)计算各航站对每个LRU的年平均需求量,根据航站的年均需求量按照(4)~(5)式计算基地的年平均需求量和年平均报废量;
2) 初始化基地的库存量,使基地的备件数量为0。
3) 按照公式(6)~(7)计算基地以及因报废产生的供应渠道数,由(18)~(19)式计算基地和因报废产生的期望短缺数EBO。

5) 由(19)~(21)式计算基地与各航站在不同库存量下的期望短缺数,并建立费效比矩阵。
(25)
6) 寻找费效比最大的位置,给费效比最大的位置库存量加一,直到机队可用度和备件保障率满足约束条件。
7) 当基地的库存量发生变化时,航站的平均补货延误时间也会发生变化,所以返回第4)、5)步更新航站的费效比矩阵。
4 算例分析
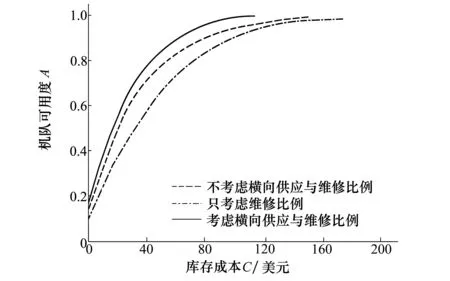
本文以某航空公司波音737客机的5个起落架LRU作为分析对象,且服从上文中的模型假设条件,机队由10架相同型号的737客机组成,年平均飞行小时为3 000 h,机队可用度最小值设为0.99。库存系统由1个基地和5个航站组成,其中航站1,2组成共享组1,航站3,4,5组成共享组2,且航站间距离D34 图5 起落架LRU库存配置系统示意图 LRU编号Mi/hCi/美元Qiρ0iρjiνiνiTsiPi(min)11 5002.7×1042.00.60.40.120.100.170.97 21 0003.3×1042.00.70.50.160.140.180.96 31 5002.9×1041.00.80.60.140.130.170.97 43001.8×1043.00.60.40.150.120.170.96 53000.5×1042.00.70.50.170.150.200.95 根据上述各航站的运营信息以及各项LRU的基本参数,由公式(2)~(9)计算基地以及各航站的年平均需求量与供应渠道数,再根据(10)~(18)式按照迭代法计算各航站的在不同库存水平下的稳态概率,由(19)~(23)式计算得到基地与各航站的期望短缺数、备件保障率以及机队可用度。由此可以建立以库存系统总成本为优化目标,以机队可用度与备件保障率为约束条件的民机起落架LRU在横向供应情况下的两级单层备件库存优化模型。通过边际分析法配置各项LRU在基地与各航站的库存数量,库存配置情况如表2所示。 表2 考虑横向供应以及维修比例的起落架LRU库存配置 由表2可知,当系统中LRU库存总数为57件时,机队可用度达到0.990 9,此时的库存配置系统的总成本为120.5万美元。 为了验证考虑横向供应与维修比例的库存配置模型的可行性与有效性,根据上述航站运营信息与表1中各项LRU的参数,分别在考虑维修比例但不允许发生横向转运以及既不考虑维修比例也不允许发生横向供应的传统配置模型2种情况下,利用边际分析法进行备件的库存配置,系统库存配置情况如表3、表4所示。 表3 考虑维修比例的非横向供应起落架LRU库存配置 由表3可知,在不允许发生横向转运时,系统中LRU库存总数需要达到87件时,机队可用度达到0.990 1,此时的库存配置系统的总成本为187.9万美元。 表4 不考虑横向供应与维修比例的起落架LRU库存配置 由表4可知,在不考虑横向供应与维修比例的传统配置模型中,系统LRU的库存总数达到76件时,机队可用度达到0.990 2,此时的库存配置系统的总成本为161.9万美元。 通过采用边际分析法对上述3种情况下的起落架LRU库存配置进行研究,可以得到3种情况分别对应的机队可用度与系统库存成本的关系曲线如图6所示。 图6 起落架LRU库存配置系统示意图 由图6可以看出,在满足约束条件的情况下,考虑横向供应及维修比例的库存配置模型与只考虑维修比例的库存配置模型以及不考虑横向供应及维修比例的库存配置模型相比,其库存系统总成本分别减少了25.6%与35.9%。这是由于允许横向供应发生时,各航站间可以直接进行备件的横向补给,各航站只需维持较低的库存数量就可以通过横向供应满足备件需求,因此其库存系统总成本相较于其他2种情况显著降低。由图还可以看出在满足约束条件的情况下本文所提出模型的机队可用度高于其他2种情况,且在相同库存成本的条件下,本文所提出模型的机队可用度最大。通过对比表2、表3的库存配置情况可以看出,同时考虑2级维修比例的情况下,当允许横向供应发生时,因为航站与基地的备件需求降低,航站的库存配置数量明显下降,基地的库存配置数量也有所降低;通过对比表3、表4可以看出各航站的库存配置情况基本相同,但当考虑维修比例这一因素的影响时,由于基地的维修比例不为无限大,在基地中存在着一定的报废量,需要重新购置备件,因此考虑维修比例情况下的基地库存配置数量明显增加;对比表2、表4还可以看出考虑横向供应与维修比例情况下的系统库存配置总数与各航站的库存配置数量都明显小于传统的库存配置模型。可以发现横向供应模式对成本的节约效果非常明显,可以为航空公司降低大量库存成本,在此基础上考虑维修比例的影响,虽然使基地的库存配置数量上升,但更符合实际工程的需求。 本文针对横向供应下的多级库存配置问题,在库存配置模型中引入维修比例这一实际因素,提出了一种考虑维修比例及横向供应的民机备件多级库存配置研究方法,并以波音737客机起落架LRU作为研究对象进行实例验证,得到结论如下: 1) 以减少库存系统总费用,提高机队可用度为目标,结合民机维修保障模式,在横向供应下的库存配置问题中引入维修比例这一实际工程因素,建立了考虑维修比例及横向供应的备件多级库存配置优化模型。 2) 在考虑2级维修比例的情况下,以某航空公司波音737客机起落架LRU作为研究对象,建立了以库存配置费用总成本为优化目标,以系统的机队可用度与备件保障率为约束条件的横向供应库存配置模型。通过分析计算,可以得到基地与各航站的备件配置数量,并且当机队可用度达到0.990 9,系统的库存配置总成本最低为120.5万美元。 3) 通过与只考虑维修比例的非横向供应配置模型,以及不考虑横向供应及维修比例的库存配置模型进行对比可以发现,所提出的模型使库存成本得到显著减少,并使机队可用度达到最高。验证了本文提出模型的有效性,证明了在库存配置问题中同时考虑横向供应及维修比例的影响更加符合工程中的实际情况,为民机备件的多级库存优化配置提供理论支撑和方法指导。



5 结 论
