飞行器圆柱类部件的气动外形参数化方法
2019-01-03何小龙白俊强李立杨体浩张煜
何小龙, 白俊强,2, 李立, 杨体浩, 张煜
(1.西北工业大学 航空学院, 陕西 西安 710072; 2.西北工业大学 无人系统技术研究院, 陕西 西安 710072)
近几十年来,波音、空客等飞机设计公司在民用客机典型布局的设计方面开展了大量研究和设计实践,使得这一类布局的气动性能潜力几乎被完全发掘出来。同时,航空业对减少燃油消耗和温室气体排放的要求越来越高,这就促使飞机各部件的设计愈加精细化,新技术和新布局的研究趋向实用化[1]。层流技术作为众多前沿技术的一种,可明显提高气动性能,有许多学者看好其前景[2-3]。在一些非升力部件上,层流技术已经实现工程实用,例如Boeing787的自然层流短舱[4]、HondaJet的层流机头设计[5]。在新布局方面,一些非传统布局性能潜力较大,也吸引了很多学者。例如使用边界层吸入(boundary layer ingestion)技术的DoubleBubble布局[6],其机身复杂曲面、短舱位置和外形都需要进行精细的设计。在飞行器设计领域以外,我国大力发展高铁技术,一些学者在高铁头部外形设计[7]中也使用了气动优化设计方法。以上设计问题都涉及到了类圆柱形物体的气动外形设计,体现出了对于径向变形和精细化设计的特殊需求。由于这种独特的设计特征,设计者需要发展更有针对性的设计方法,尤其是几何外形参数化方法。
作为气动优化设计方法的重要组成部分,参数化方法在近年来发展出了多种针对机翼类部件的较为成熟的具体方法[8],但仍缺少专门针对圆柱类物体开发的参数化方法,在参数化描述能力、灵活性、便捷性方面还需要改善。基于CAD软件的方法[9]、基于non-uniform rational b-spline(NURBS)的曲面参数化方法[10]、class shape transformation(CST)[11]、free-form deformation(FFD)[12]等几种方法得到了广泛应用,但是将之用于圆柱类问题中仍存在一定局限性,例如NURBS方法可以用于圆柱类外形设计,但是考虑到参数化的发展方向是具备针对全机构型等复杂构型的参数化能力,而 NURBS需要对复杂曲面、相交曲面进行处理,因此难以拓展应用于更复杂的外形中;Kulfan等人基于CST方法研究了机身气动特性[13],Fang、Robinson等人分别研究了基于CST的短舱设计方法[14-15],参数化能力良好,但是CST方法在复杂曲面和相交曲面上应用也有一定难度;何小龙等人使用EFFD方法对单独短舱剖面进行参数化并进行轴对称自然层流短舱设计,但是缺少对三维非轴对称短舱外形的研究[16]。以上方法都是在笛卡尔坐标系下进行变形,对于圆柱体径向变形的处理能力偏弱。参数化方法的研究还需要考虑到如何拓展应用于复杂构型,例如对于机翼-挂架-短舱构型的设计问题,FFD具有使用便利的优势,因此在此类构型的优化设计中已经有所应用[17]。
FFD最早由Sederberg于1986年提出[12],早期主要应用于计算机图形学方面,引入气动优化方向以后也得到了较为广泛的应用。NURBS free-form deformation(NFFD)[18]是其中应用较多的一种改进。虽然NFFD可使用圆柱形控制框,但仍然是在笛卡尔坐标系下进行变形。一方面,二者对于圆柱类物体的参数化能力弱,变形特点不适应于圆柱外形;另一方面,对于框的边界处的导数连续问题的处理方法难以用于圆柱物体[12]。为了得到光滑连续的外形,导数和曲率连续特性是需要考虑的因素。Ahn等人提出了一种基于修改公式的使用圆柱形控制框的FFD方法[19],在圆柱周向使用二次B样条以保证周向导数连续。此方法是在笛卡尔坐标系下进行变形,变形特点并不理想,而且对公式进行了修改,只能局限于对圆柱类外形的应用。
本文在NFFD方法基础上,增加坐标转换步骤并使用虚拟框策略,从而将NFFD扩展为适用于轴对称和非轴对称圆柱外形的CYFFD方法,对比分析了二者的变形能力、导数保持能力,并进行若干参数化变形、拟合、优化示例研究。
1 CYFFD方法
在圆柱形物体上直接使用NFFD方法主要有2个方面的问题:
1) NFFD的变形方式着重于沿坐标轴方向或三者的线性组合,在圆周向或直径方向的变形能力较弱,或者需要繁琐的特殊处理,因此会导致所需要设计变量的数目较多、适用性较差;
2) 为了对圆柱表面外形进行精细设计,生成控制框,如何对控制框边界处的外形进行设计并且保持曲率连续是一个需要解决的问题。
针对这两方面的问题,本文基于Lamousin等人提出的NFFD[18]方法,引入坐标转换和虚拟框方法得到了CYFFD方法。本节首先对CYFFD进行介绍,后文将对二者进行详细的对比分析。CYFFD所使用的核心公式与NFFD类似,其使用步骤与NFFD基本相同,主要差异来源于新引入的坐标转换和虚拟框方法,具体使用步骤如图1所示。
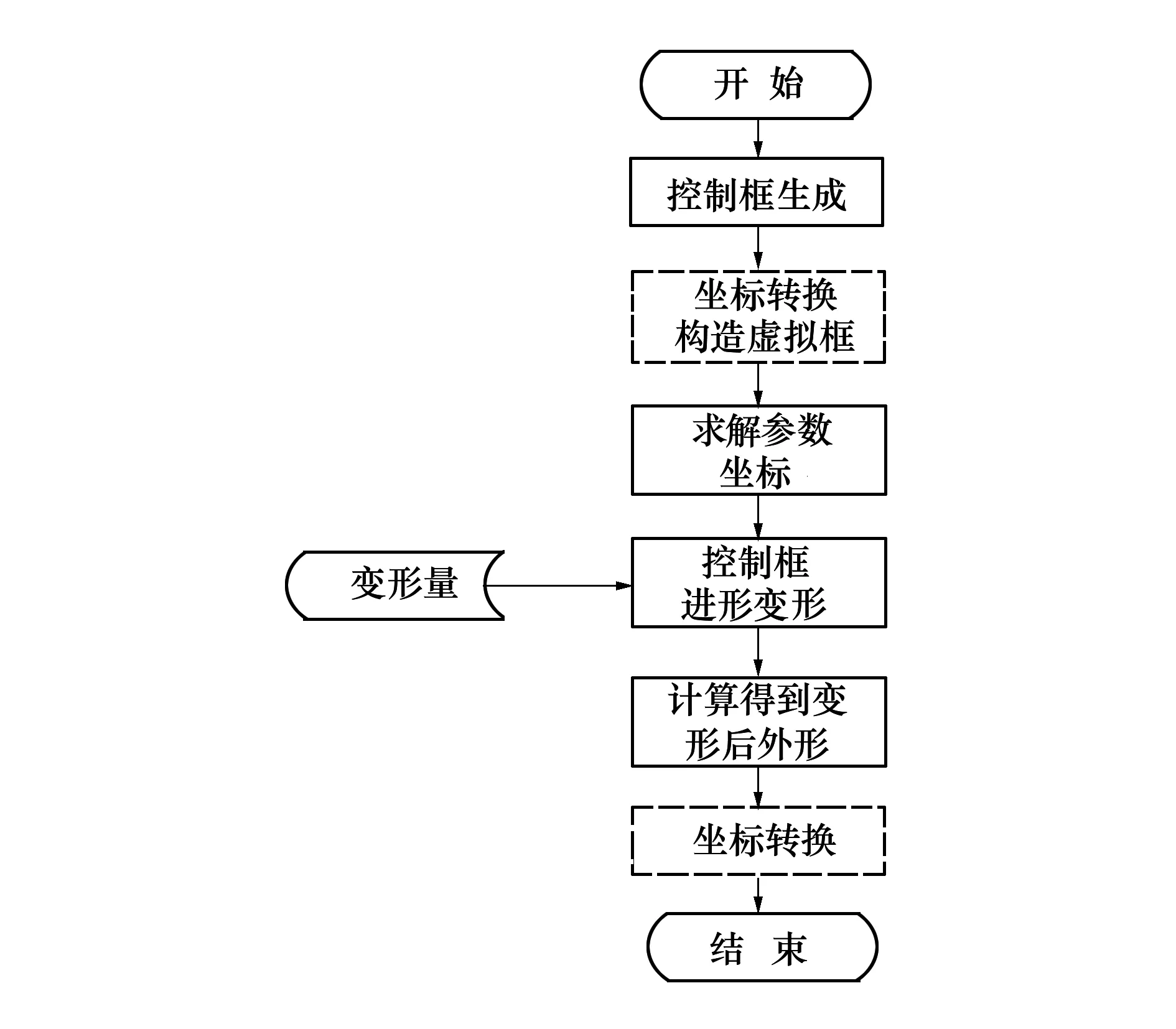
图1 CYFFD使用步骤示意图
(1) 建立CYFFD控制框对于表面任意一点的全局坐标X,也就是几何外形的笛卡尔坐标。在全局坐标下建立一个或者多个FFD控制框Pi,j,k=(xi,j,k,yi,j,k,zi,j,k),控制框沿着i,j,k3个方向分别有l+1,m+1,n+1个控制点。另外,还需要为控制框指定圆柱坐标系的原点和坐标方向。
(2) 坐标转换、虚拟框生成
将控制框的坐标P、变形目标坐标X转换到圆柱坐标系下。坐标转换公式如公式(1)所示,其中T是坐标转换函数。
Pcy=T(P)
Xcy=T(X)
(1)
选取若干个控制点作为虚拟控制点,形成增广的控制框Pcyex。坐标转换和虚拟框的具体方法见下文。
(3) 求解参数坐标
使用Pcyex,Xcy形成映射公式(2),并使用牛顿迭代方法求解得到参数坐标(ucy,vcy,wcy)。
Xcy(u,v,w)=
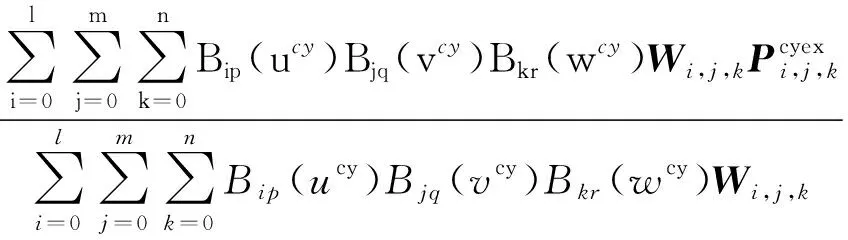
(2)
式中,Wi,j,k是每个控制点的权重系数,Bip,Bjq,Bkr分别是p,q和r阶(p+1、q+1和r+1次)NURBS基函数。
(4) 对控制框进行变形
(5) 得到变形后的曲面

(6) 坐标转换

1.1 坐标转换方法
假设生成的控制框如图2所示,其中的全局坐标系即笛卡尔坐标系oxyz,与框固连的笛卡尔坐标系o′x′y′z′,以及图3显示的基于圆柱框建立的圆柱坐标系oθrh。
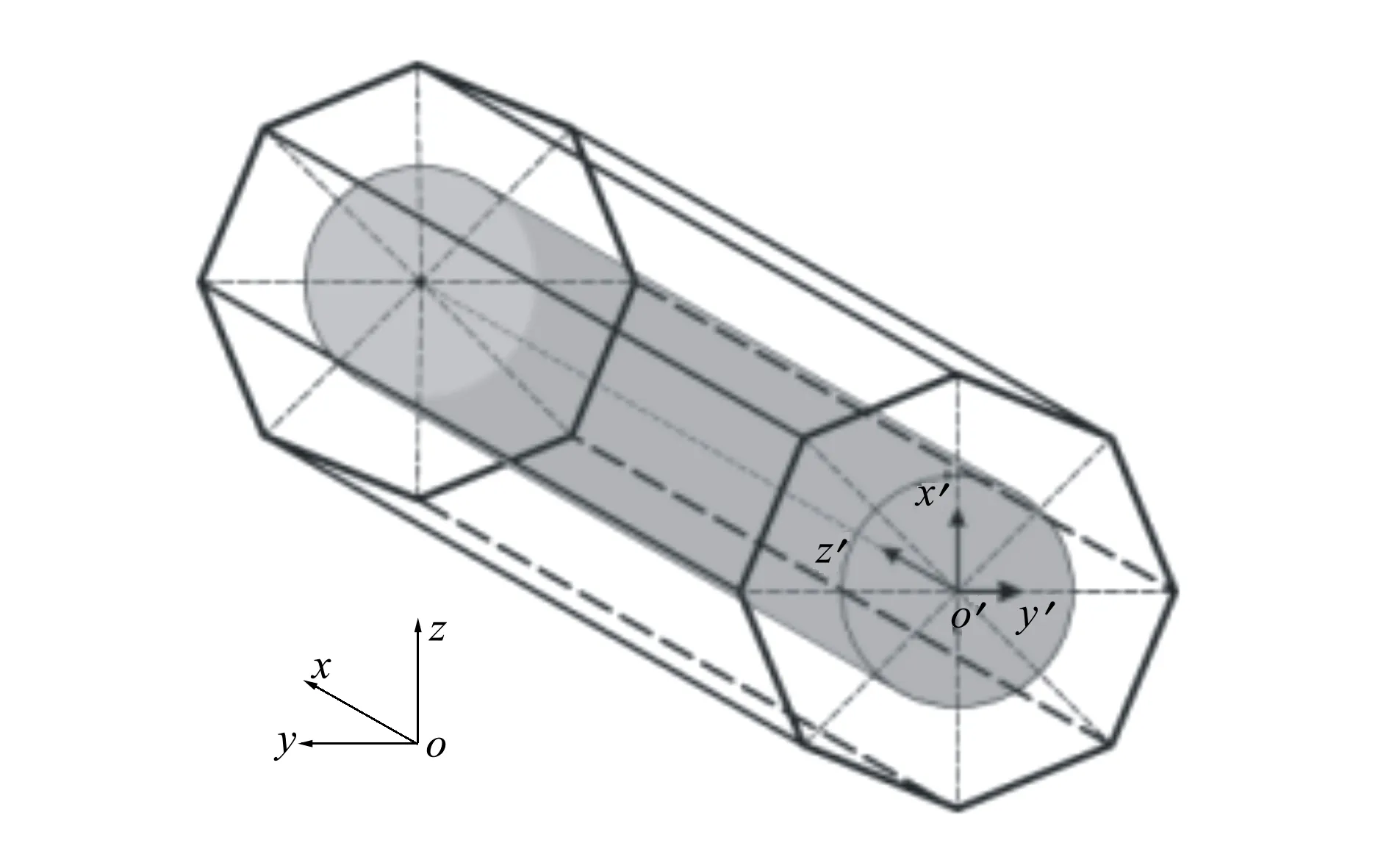
图2 CYFFD控制框示例
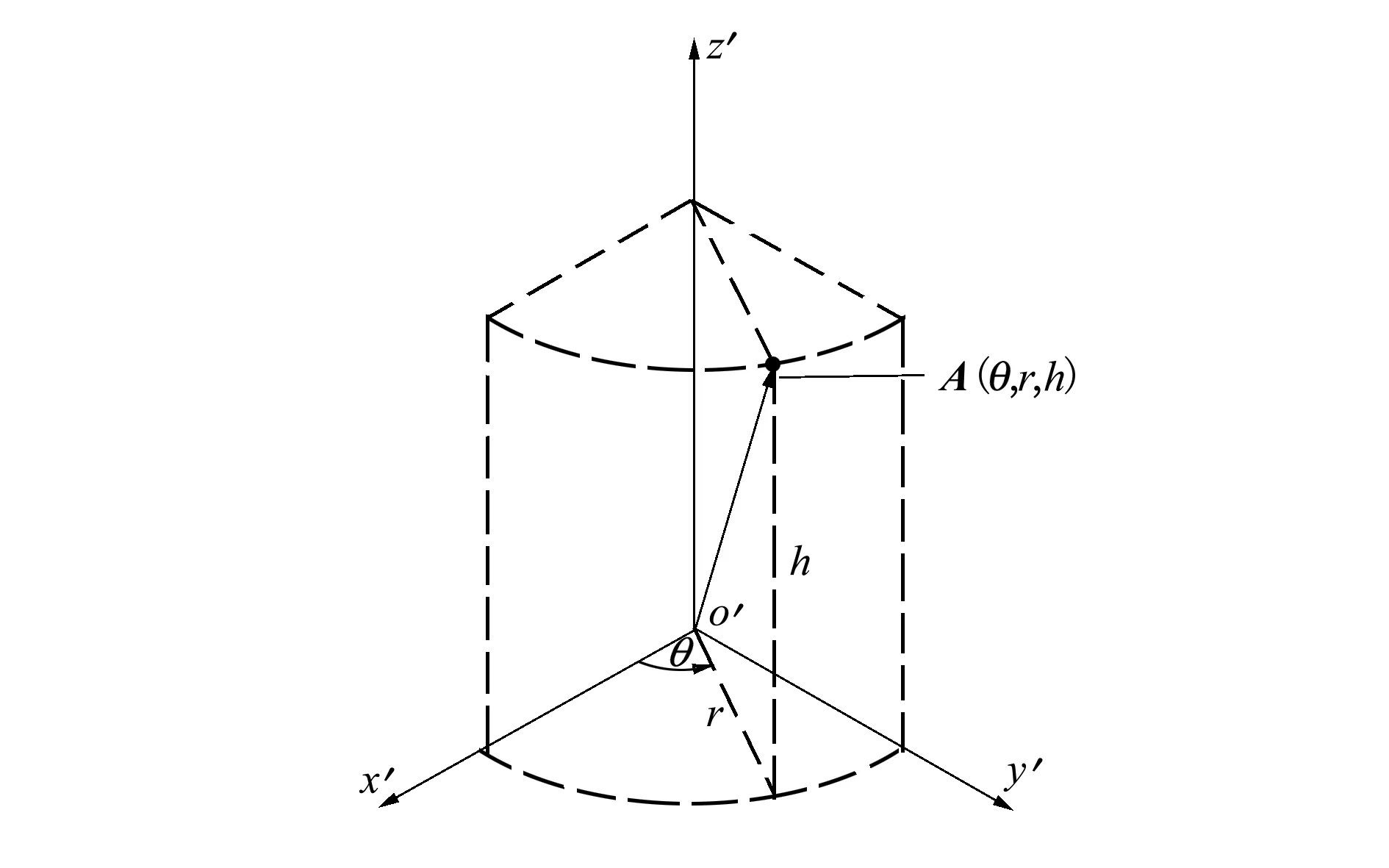
图3 圆柱坐标系布置
笛卡尔坐标系转换到圆柱坐标系的过程可分为2个步骤:①从oxyz向o′x′y′z′的转换,包括平移和旋转;②从o′x′y′z′向oθrh转换。该转换过程以及逆向转换过程见公式(3)定义。
Acy=T(A)=T2(T1(A))
(3)
其中点A=(x1,y1,z1)T是oxyz坐标系下任意一点,Acy是A在oθrh坐标系中的坐标,o′x′y′z′的坐标原点在oxyz中的坐标是o′=(ox1,oy1,oz1)T。公式(3)中的坐标转换函数T及其反函数T-1的定义如公式(4)所示:
(4)
式中,A′是A在o′x′y′z′中的坐标,P-1,Q-1分别是P和Q的逆。P的定义如公式(5)所示:
(5)
式中,e1,e2,e3是oxyz的坐标轴方向单位矢量,f1,f2,f3是o′x′y′z′的坐标轴单位矢量。
Q是变换函数,其作用是实现公式(6)所示的映射:
(6)
1.2 虚拟框方法
为了获得光滑连续的几何外形,导数和曲率连续是外形设计中需要考虑的问题。因此需要一种方法既能够实现对圆柱类外形的变形,同时保持导数、曲率连续。根据FFD理论,在控制框边界处,如果想要保持导数和曲率连续,则需要保持边界处和相邻的一些控制点坐标不变[12],这一要求会使得这些控制点无法移动,也就无法作为参数化的设计变量。
图4显示了一种针对圆柱类外形的控制框布置形式,图中实线是控制框边界,虚线是控制框内部,粗线是首尾重合的两端边界。如果框包裹着圆柱类外形,粗线就必然和外形相交。如果使用NFFD并移动粗线上的控制点,曲面和粗线相交的位置就会存在导数连续性问题。虚拟框方法就是针对这一问题提出。
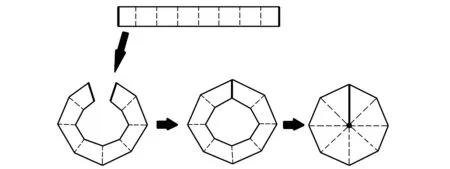
图4 圆柱框拓扑示意图
虚拟框方法利用一些控制点作为虚拟控制点,从而形成一个增广框,也就使得曲面外形被完全包裹在控制框中。图5显示了一个控制框示例和虚拟框点的选取方式,其中包裹着一个圆形作为变形目标。其中C,D,E,F,G,H,I,J,K是人工布置的控制框点,A,B,L,M是取I,J,D,E的周向坐标,然后叠加2π得到。这些点在笛卡尔坐标系下会重合,而在圆柱坐标系下会分散开来,如图5下方的直线所示。
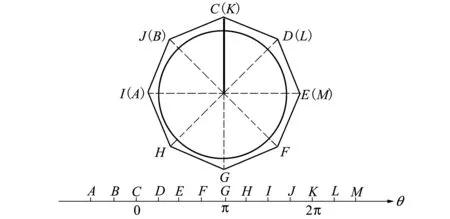
图5 周向虚拟框控制点选取示例
图6显示了虚拟控制框在圆柱坐标系下的情况。沿着角坐标θ,阴影区域对应着用户生成的控制点坐标,而浅色区域是虚拟控制点覆盖的区域。虚拟控制点的数目会影响在边界处的连续性的阶数,如采用一个虚拟控制点,则可保持导数连续,此处示例采用2个虚拟控制点,可以保证曲率连续,这一点可以类比NFFD的导数连续性条件。

图6 圆柱坐标系下三维虚拟框示例
虚拟框方法要求在框变形的步骤中进行特殊处理:如果I,J,D,E的点坐标发生变化,A,B,L,M也随之移动。例如保持I和A之间的2π角坐标差量不变,以及径向、周向坐标保持相等,在笛卡尔坐标系下I和A会始终保持重合。
另外,虚拟框方法也可以用于多个控制框交界处,用于保持多个控制框之间的导数或曲率连续。
2 NFFD与CYFFD对比分析
本节通过理论和变形示例的分析,对比NFFD和CYFFD在变形能力、导数保持特性两方面的异同。
2.1 坐标变换的意义
本节通过分析参数空间的形状,分析坐标变换方法对CYFFD变形能力的影响,并与NFFD进行对比分析。图7、图8中的阴影区域是参数坐标(ucy,vcy,wcy)各自取值为[0,1]所覆盖的参数空间,这个空间的外表面就是ucy=0,ucy=1,vcy=0,vcy=1,wcy=0,wcy=1的6个曲面。此处基函数都使用了均匀节点矢量,并在节点矢量起始和结束位置使用多重节点。在这个空间中,控制点与曲面点的距离越近则影响越大。其中的粗实线表示框的边界,虚线表示框的内部线。假设θ为顺时针方向,如图7a)所示。
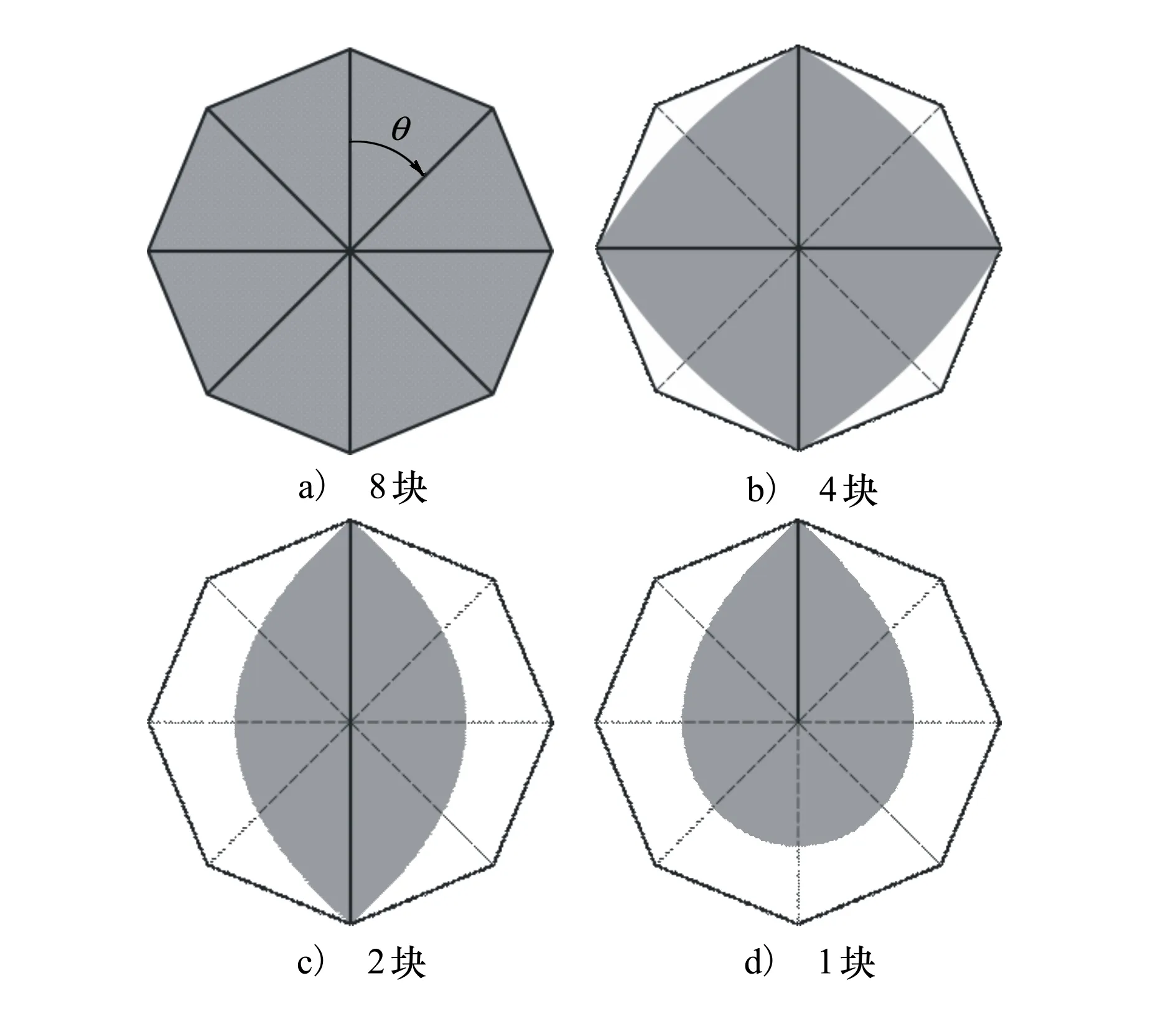
图7 NFFD控制框的数目对参数空间的影响
图7显示了8个、4个、2个、1个NFFD控制框的情况。图7b)中,θ=0°和θ=45°这2个位置的控制点的控制能力明显不同。图7c)、图7d)分别显示了2个及1个控制框的情况,如果θ=45°,θ=135°等位置的控制点进行径向变形,会导致外形发生非轴对称的变形,丧失了基础外形的轴对称特性。另外,这些控制框布置方式都无法保持曲面跨边界的导数连续特性。
图8显示了CYFFD的参数空间形状不受控制框的数目影响,每一个控制点对外形都有着近似相同的影响。而且,即使沿着θ方向非均匀布置控制框,其参数空间仍然会是相同的圆形,不过其变形效果则会是非面对称的。
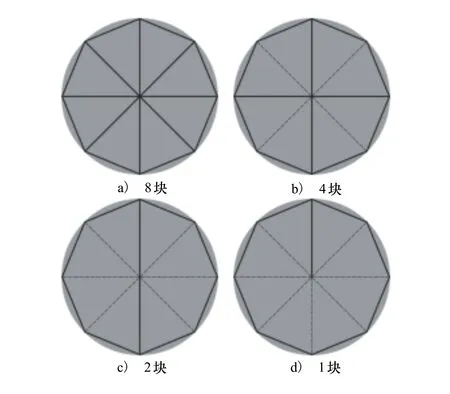
图8 CYFFD控制框的数目对参数空间的影响
从以上观察可以看出,NFFD用于圆柱外形参数化时对控制框布置形式非常敏感,各控制点的影响有所差异,而且边界位置的导数连续性难以保证;CYFFD则对控制框布置形式相对不敏感,各控制点影响基本类似。
2.2 虚拟框方法的作用
本节使用圆柱示例来对NFFD和CYFFD在处理框边界处导数连续性的能力进行对比分析。图9显示了控制框的布置情况,图中与若干控制点重合的圆形就是目标外形,而四周的圆形点就是控制点。对于NFFD,布置多块组合控制框如图9所示,图中的阴影区域就是一个块,沿着θ方向布置了8个块。虚线及其联接的控制点是变形后的控制框点,其z方向位移作为设计变量。而CYFFD和NFFD使用同样的控制点,区别只是把所有块都合并为1个块,并使用2个虚拟控制点,拓扑结构类似于图4所示。

图9 控制框布置
图10a)显示了控制点的变形量为0.1,0.3,0.5时,NFFD及CYFFD的变形结果截面,圆形实线是基础外形。图10b)中显示虚线方框处的放大图,从中可以看出,随着变形量增大,NFFD在控制框边界处的导数不连续问题愈加明显和严重,而CYFFD始终保持了导数连续。
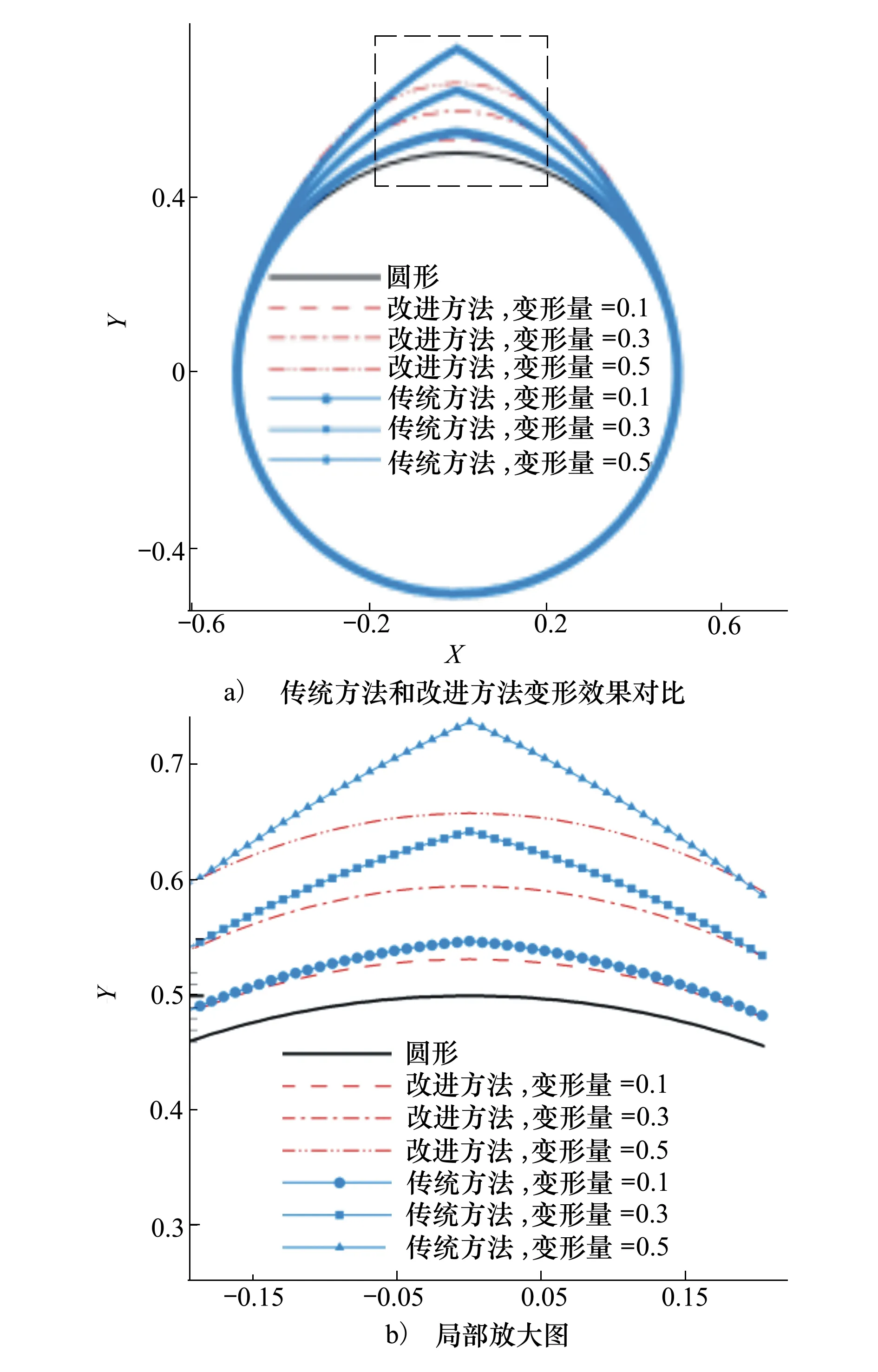
图10 NFFD和CYFFD变形效果对比
3 CYFFD变形示例
有一些学者进行过FFD参数化方法等方法的拟合目标翼型的对比研究[20],表明了FFD方法对于翼型的描述能力较强。对于CYFFD,每个圆周向位置都可以视作一个翼型截面,沿着径向进行变形也就等效于在这个截面内对翼型进行变形,因此CYFFD在这个截面内会具有与NFFD类似的变形能力。对NFFD的拟合测试结论在一定程度上可以代表CYFFD对周向任意截面的参数化能力,亦即轴对称曲面的参数化能力。
本节通过选取若干变形算例、短舱外形拟合算例、优化算例测试来说明CYFFD的参数化性能。
3.1 圆柱示例
第一个示例采用直径为1的圆柱曲面外形进行变形测试。控制框布置如图2所示,周向的首尾各自使用了2个虚拟框点,即图5所示。从图11b)可以看出CYFFD可以单独进行严格的径向变形,而且能够保持轴对称特性;图11c)表明通过控制点的周向移动,可以实现扭转变形;图11d)表明通过径向、周向、轴向组合控制方式,能够变形得到复杂的曲面外形,且变形结果在各个方向都光滑连续。
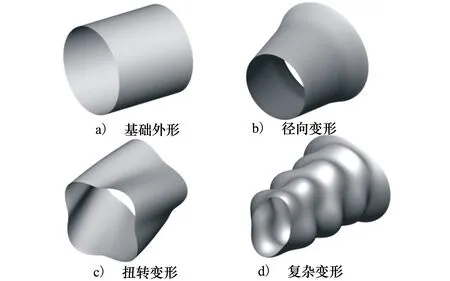
图11 圆柱变形示例
3.2 机身参数化示例
机身参数化示例演示了CYFFD变形和NFFD变形的组合使用,目的是表明二者可以协同工作,从而实现复杂的变形目标。由于CYFFD主要在圆柱坐标系下工作,因此无法实现平移、缩放、旋转等笛卡尔坐标系下的操作,所以此算例的目的在于验证CYFFD和NFFD协同使用的能力,既具备圆柱坐标系下的变形能力,也不会损失已有的NFFD变形能力。
这里选用了圆柱加半球的基础外形如图12a)所示,布置控制框并使用CYFFD进行变形和拉伸得到中间结果如图12b)所示,然后使用NFFD进行变形,从而得到类似于飞机头部外形的曲面图12c)所示。需要说明的是:CYFFD和NFFD可以各自独立使用,也可以组合使用,这里只是用这个例子说明CYFFD具备与NFFD组合使用的能力。

图12 机身变形示例
在这个例子中CYFFD及NFFD被先后使用,在其他情况下可以将二者同时使用。假设存在多个控制框时,可以对其中一些控制框使用NFFD,而对另外一些控制框使用CYFFD。例如对于机身-机翼-挂架-短舱构型,可以布置多个控制框,机翼和挂架使用NFFD,而机身和短舱可以使用CYFFD。
3.3 短舱变形示例
第三个算例是短舱变形示例,目的是考察CYFFD在工程应用中的效果。圆形的发动机进气道有助于实现更高的进气质量,例如发动机设计者需要考虑总压畸变等指标。但是在实际工程中,会由于存在一些其他工程约束导致短舱外形无法制造为轴对称外形。例如Boeing737客机的发动机尺寸增大导致距离地面过近,因此选用了非轴对称短舱外形。
此处采用CYFFD进行径向的变形,从而得到类似于Boeing737客机短舱的非轴对称外形。以DLR-F6模型[21]的短舱为基础外形,布置控制框如图13a)所示,变形结果如图13b)所示。在这个示例中,CYFFD将通过截面控制点进行短舱截面精细变形,通过若干控制点的平移实现较大范围变形。
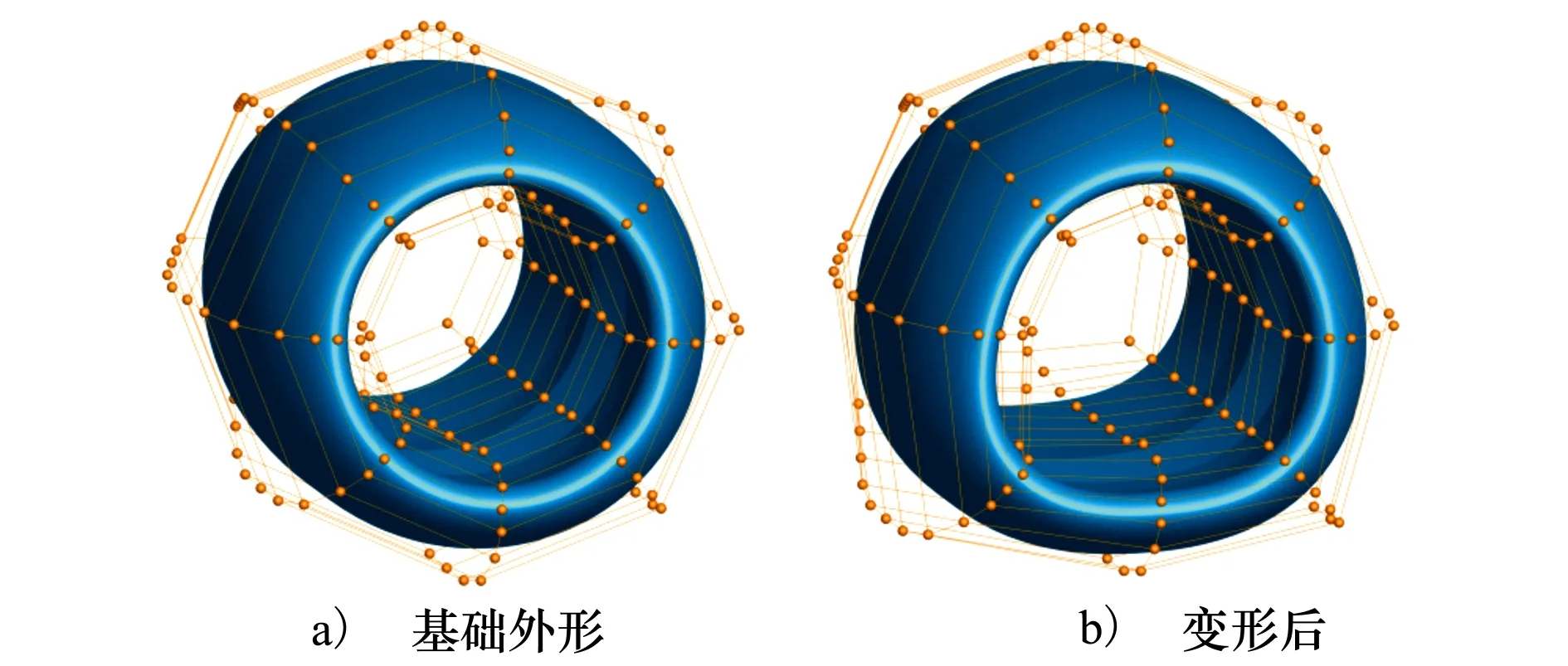
图13 短舱变形示例
3.4 短舱外形拟合示例
本节采用短舱外形拟合算例,以说明CYFFD对于非轴对称短舱的参数化能力。
拟合目标采用common research model(CRM)的机翼-机身-挂架-短舱构型中的短舱外形。实际操作中需要单独取出其中的短舱外形,并填补缺失的挂架位置的曲面。前缘唇口的近似圆心作为坐标系原点,并旋转短舱使得出口面垂直于x轴,坐标系方向见图14。该短舱外形近似圆柱,但仍然是一个非轴对称外形。
基础短舱外形采用CRM短舱的唇口和后缘构造线,并在各个周向位置使用NACA0008翼型生成曲面。
拟合结果命名为拟合短舱(fitted nacelle)。拟合操作采用最小二乘拟合的方法,所需要求解的方程组为Ax=B。雅克比矩阵A的每一项是:任一点的x坐标(y,z同理)对于某个设计变量(此处就是控制点位移)的偏导数,使用(2)式右端项并舍去控制点Pcyex即可计算得到,B是目标外形和基础外形的坐标差值向量。假设短舱表面点数为m,FFD框的设计变量数目为n,那么A是3×m行(三维空间)、n列,x是n行的列向量,B是3×m行的列向量。使用最小二乘法求解得到解x,进行框变形就得到拟合短舱的外形。
图14显示了变形前后的外形和控制框,可以看出拟合外形和目标外形非常接近,CYFFD拟合效果良好,证明其参数化能力较强。为了提高对头部的拟合能力,在接近唇口处布置更密集,在弦向的其他位置使用近似均匀分布的控制点。
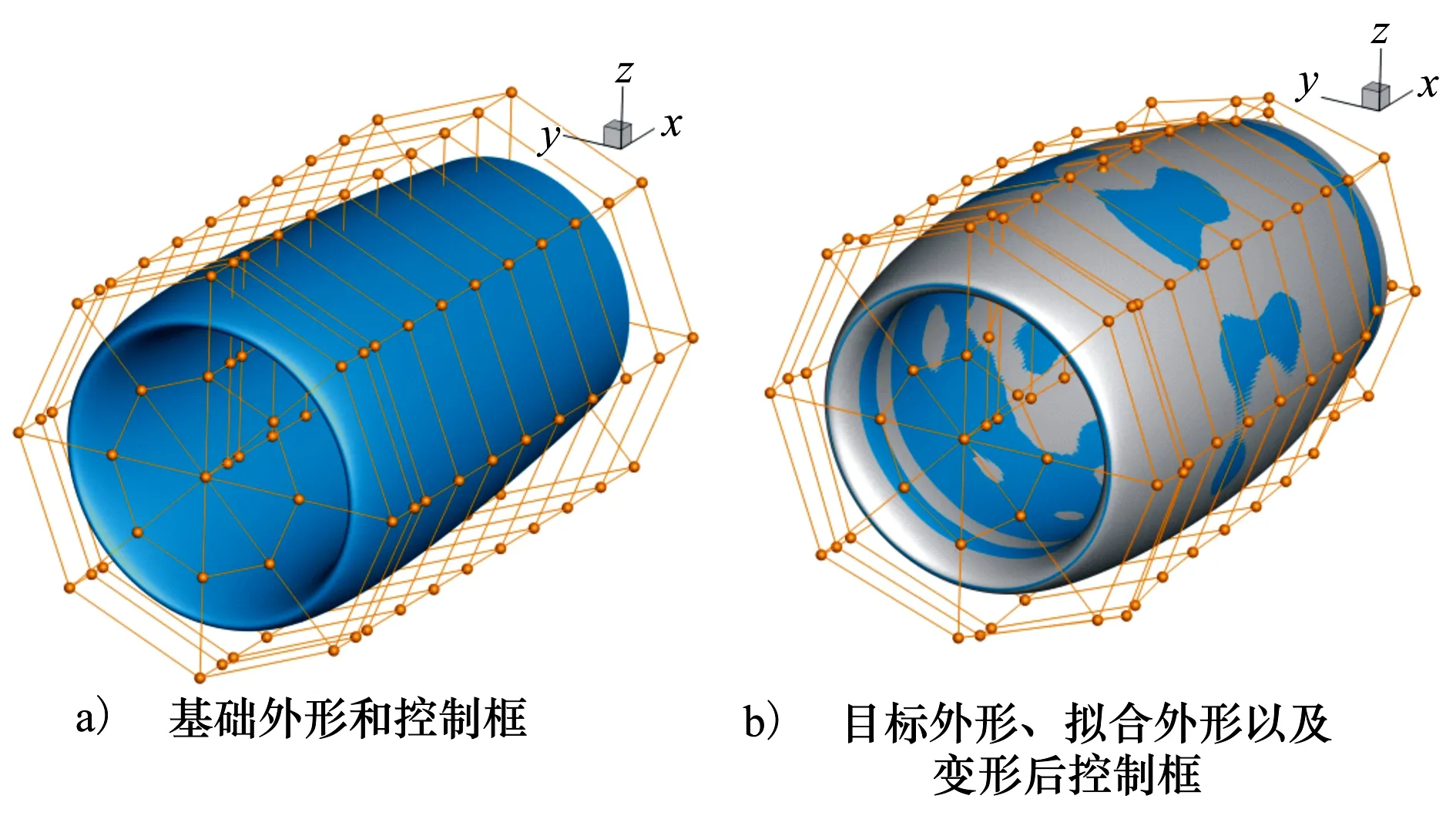
图14 拟合前后的短舱、控制框对比
图15a)、图15b)显示了z=0和y=0平面的短舱截面,即半径最大处的纵向截面和横向截面,可以看出拟合短舱和目标短舱的截面几乎重合,最大误差出现在唇口位置,在其他弦向位置的拟合误差极小。更多的控制点或者更优的控制点分布会有助于减小拟合误差。对于本测试算例而言,该测试结果已经可以表明CYFFD参数化能力较强,拟合效果良好。
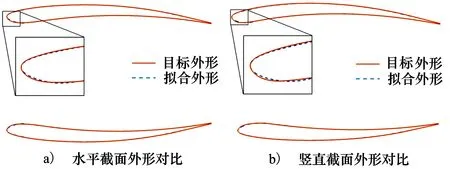
图15 目标和拟合短舱对比
3.5 圆柱头部优化算例
本节对一个圆柱头部外形进行气动优化设计,以初步验证CYFFD的实用性并测试优化设计的效果。本方法的后续研究内容是层流短舱、层流机头、机身后体等优化设计问题,因此这里只采用了圆柱头部作为初步的验证算例。
本算例的几何外形和设计工况均为作者所选取,头部外形长度1 m,等直段长度2 m、半径0.4 m,尾部长度1 m,整个外形是轴对称的旋成体。头部几何形状可用表达式r=0.4x0.5描述,其中的r是旋成体半径,x取值范围是[0,0.9]。x=[0.9,1.1]的范围内,使用样条形成头部和等直段的光滑过渡,尾部外形用Von Karman曲线,几何外形如图16中小图所示。
设计状态是:Ma=0.8,攻角为0°。流场求解采用团队开发的Euler求解器,使用二阶中心差分格式、diagonally dominant alternating direction implicit(DDADI)隐式算法,并使用多重网格和隐式残值光顺以加速收敛。计算网格如图16所示,物面第一层网格高度1×10-3,圆形远场直径约120 m,网格单元总数约12万。计算参考面积3.2 m2。
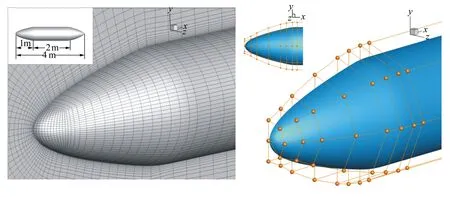
图16 头部外形及网格 图17 控制框布置
使用序列二次规划优化算法、基于反向距离插值的动网格方法、基于伴随方法的梯度求解方法以及本文提出的CYFFD方法构建优化设计系统,所涉及的以上方法及代码详细介绍见文献[22]。优化设计问题数学模型建立如下:
minCd
w.r.txshape
FFD控制框布置如图17所示。设计变量xshape是每个等x截面内的控制点径向位移量,变形效果是使圆柱半径缩小和放大,头部的前7个截面作为设计变量,无几何约束。对于这种控制框布置,如果只使用一个块,使用NFFD也可以进行变形和优化,不过在对称面位置会存在导数不连续问题,也就是对称面会出现一个导数间断的棱。此算例用来验证CYFFD的变形特征和用于优化的可行性。
优化收敛历史如图18所示,图中中显示了阻力收敛曲线。优化后阻力参数从0.001 85减小至0.001 13,优化结果可以说明CYFFD能够良好地实现参数化并用于优化设计。
优化结果与初始外形的对称面几何和Cp对比如图19所示。优化后的头部中段外形更加饱满,这一几何特征削弱了在x=1.0附近的急剧气流加速,使得Cp峰值减小,激波得以削弱,因此阻力得以减小。

图18 优化收敛历史图19 优化结果与初始构型对比
优化前后的马赫数云图对比如图20所示。根据等压线分布来看,初始构型在x=1.0附近相对密集,而优化后更加稀疏,与Cp图趋势对应,表明激波强度有所减弱。
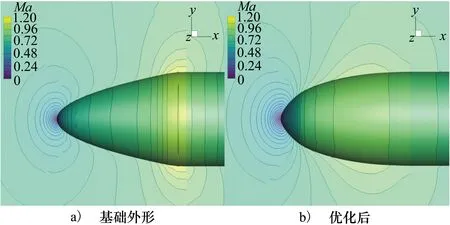
图20 优化前后马赫数云图对比
4 结 论
CYFFD采用和NFFD相同的核心映射公式,并使用坐标转换和虚拟框2种辅助方法提高了对于轴对称和非轴对称圆柱外形的参数化能力,是对NFFD功能的扩展。经过圆柱外形示例、机身头部变形示例、短舱变形和拟合测试、圆柱头部气动优化算例,研究得到以下结论:
1) 使用坐标转换方法可使CYFFD具备良好的径向、周向变形能力,能够充分捕捉圆柱类外形的变形特点;虚拟框方法实现简单、效果良好,在所有测试算例中都能够保持一阶导数、曲率连续,变形后曲面光滑连续,参数化能力较强。
2) CYFFD能够和NFFD交替使用或者组合使用,可以提供对多部件、多特征复杂构型的参数化能力,其描述能力、灵活性、通用性较强。
3) CYFFD用于目标外形拟合和气动优化设计都能够达到良好的效果,在飞行器圆柱类部件的精细化设计问题中具有一定工程实用价值。
