基于M-CFSFDP算法的战场目标分群方法

李伟楠, 章卫国, 史静平, 吴云燕

(1.西北工业大学 自动化学院, 陕西 西安 710072; 2.航空工业自控所, 陕西 西安 710065)

态势估计通过感知战场环境和敌我目标信息,推理敌方意图,预测敌方行动,从而辅助指挥人员做出正确决策,奠定战场胜局[1]。然而,现代战争中存在数量众多、种类繁杂、属性多样的敌我战场目标,这些都导致了信息量激增,从而对态势估计提出了挑战。而目标分群能够根据目标自身属性、目标间的空间关系,将目标分类合并为互不相交的空间群体,大大减少冗余信息,从而降低态势估计难度,提高决策效率。

战场目标分群问题具备以下特点:①空间群数量未知。由于战场敌方目标部署情况未知,而我方目标部署又可能针对敌方发生改变,因而敌我双方目标分群的空间群数量是未知的。②目标属性多样。目标具备多种属性,如位置、速度、航向等,使得目标分群面对的数据往往是高维的。③目标分群动态性。战场战况瞬息万变,目标的状态也在时刻改变,从而导致目标所属空间群的改变。目标分群问题不单是对应某一时刻的静态分群,还是对应一段时间甚至整场战争的动态分群。

针对战场目标分群问题,文献[2-3]对目标属性如位置、速度等建立相似度函数,然后构建空间相似度矩阵来进行目标分群。然而,多个相似度函数中引入了相似度计算阈值,空间相似度矩阵中又引入了相似度判定阈值。过多的阈值,会因为某些阈值取值不当而影响算法效果。文献[4-6]将目标分群看作聚类问题,分别利用k-means算法和chameleon算法进行求解。然而,文献[4]在确定空间群个数时,需要人为指定合理分群数的上限。但是在一些复杂战况下,指挥人员可能无法指定该上限;文献[5-6]则是在合并相邻群时,必须人为指定相对互连性和相对近似性所需要满足的阈值,但文中并未给出指定的依据或方法。最后,上述文献都只是对某时刻战场目标进行静态分群,并未进行动态分群仿真。

本文结合目标分群问题的特点,提出了一种基于M-CFSFDP算法的目标分群方法来将战场目标划分为空间群。首先,建立战场目标分群问题模型,并将其转化为数据集聚类问题。其次,目标分群的特点要求聚类算法能够在类别数量未知的前提下,解决高维数据的动态聚类问题。CFSFDP算法[7]能够自动搜索与发现聚类中心,且可以对高维数据进行聚类,并且已经被用于目标分群问题中[8],故选择CFSFDP算法来实现聚类。再次,针对CFSFDP算法中的欧氏距离无法正确衡量目标之间相似性的问题,提出引入流形距离将CFSFDP改进为M-CFSFDP。最后,应用M-CFSFDP算法对人工数据集和UCI数据集进行聚类仿真实验,并对战场目标进行静态与动态目标分群仿真实验,仿真结果证明了M-CFSFDP算法的正确性与可行性。

1 问题描述

目标分群的输入为战场中的各目标的状态信息,如位置、速度、航向等。某时刻战场目标集合可表示为:

T={O1,O2,…,On}

(1)

式中,Oi表示一个目标,n为目标的数量。对于一个目标Oi,其状态属性可表示为一个多元组:

Oi={xi1,xi2,…,xim}

(2)

式中,xij表示第i个目标的第j个属性值,m为属性的数量,即一个目标对应m维空间的一个点,T对应m维空间一个具有n个点的点集。

本文所需解决的问题,就是根据战场中所有目标的自身属性值,以及目标之间的时空关系,将它们分解到多个互不相交的空间群中,即

∀i≠j,ψi∩ψj=∅

(3)

式中,ψi表示一个空间群,N为空间群的数量。每个空间群由至少一个目标组成。

2 基于流形距离的CFSFDP算法

2.1 CFSFDP算法

CFSFDP算法针对聚类中心提出了2点假设:①聚类中心的局部密度大于其近邻点;②聚类中心距高于其局部密度的点较远。这2点假设实际上描述了聚类中心所具备的2条特性:自身局部密度大,以及聚类中心之间的距离远。而非聚类中心的样本点则只具备其中一个特性,或者都不具备。

1) 局部密度

对于数据集X=[x1,x2,…xn]中的一个点xi,其局部密度定义如(4)式所示:

(4)

式中，dij为数据点xi与xj之间的欧氏距离,dc为截断距离,χ(·)为核函数。核函数可选择3种形态[9]:

(1) 截断核

(5)

(2) 高斯核

(6)

(3) 指数核

(7)

由此可见,以数据点xi为中心,以截断距离dc为半径所划出的一个区域,该区域在二维或三维空间对应一个圆形或球体,在高维空间对应一个超球体。核函数则决定了xi以外的点处于该区域内的概率。局部密度实际上是概率的和,表示了点xi周围近邻点的密集程度。

2) 高密度近邻点距离

高密度近邻点距离定义如下:

(8)

对于点xi,xj是所有局部密度大于该点且与该点距离最近的点。xi与xj之间的欧氏距离即为高密度近邻点距离。如果xi是局部密度最大的点,其高密度近邻点距离为:

δi=maxi(dij)

(9)

3) 截断距离的求取

在求取局部密度时,关键问题就是截断距离dc的取值。文献[7]仅给出dc的经验性取值范围。然而该范围过大,需要人工筛选,不利于算法的自动化;与此同时,对于某些数据集,合适的dc甚至不在该范围内。文献[10-11]中介绍了数据场的概念并应用在数据聚类中,文献[12]则在数据场的基础上利用信息熵给出了自动求取dc的方法。

该方法将数据集等价为一个数据场,将数据点的局部密度ρi等价为该点在数据场中的势能函数φi,其定义如下

(10)

式中,影响因子σ即为截断距离dc。

然后,利用信息熵H来度量整个数据集的不确定性,其定义如(11)式所示

(11)

信息熵与数据集的分布相对应,熵值越小,不确定性越小,数据集越符合其真实的分布方式。当σ从0到+∞增加时,H先从Hmax=log(n)减小,在某个σ处达到最小值,然后又增大到Hmax。在H达到最小值时对应的σ,即为最优dc。

综上所述,CFSFDP首先计算各个数据点的局部密度ρi以及高密度近邻点距离δi,然后构建ρ-δ决策图来快速寻找和发现聚类中心,最后指定剩余点的类别,其类别与高于该点局部密度且距该点最近的点相同[13]。

2.2 基于流形距离的CFSFDP算法改进

2.2.1 CFSFDP算法的缺陷

CFSFDP算法搜寻聚类中心时主要依靠ρi和δi,而δi的求取则依赖于ρi。因此,ρi的正确求解直接决定了CFSFDP算法聚类结果的正确性。在求取ρi时,其核心为首先利用数据点xi与xj间的欧氏距离来衡量xi与xj的相似性,然后通过核函数将相似性转化为ρi。因此,数据点间的欧氏距离越小,相似性越大,ρi越接近1;反之,欧氏距离越大,相似性越小,ρi越接近0。然而,对于很多数据集,尤其是高维数据,欧氏距离却无法正确衡量数据点之间的相似性。某数据集一部分数据空间分布如图1所示:

图1 欧氏距离和流形距离的相似性度量对比图

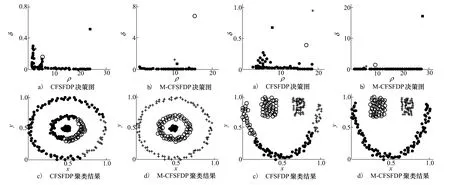
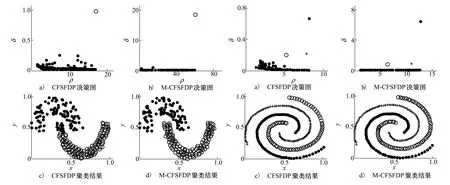
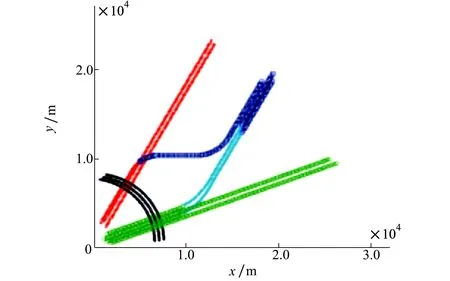
由图1可知,a与c属于同一类,而b属于另一类。然而,a与b之间的欧氏距离dab为0.209,a与c之间的欧氏距离dac为0.458,且dab

究其根本原因,是由于数据集的样本点在空间内不再是简单且彼此隔离的球状簇集,而是形成一个个彼此相连的复杂结构,统称为流形[14]。针对流形结构明显的数据,数据点之间的最短距离并非欧氏距离,而是测地距离,即流形距离。此时,只有采用流形距离才能正确衡量数据点之间的相似性。

2.2.2 M-CFSFDP

空间上xi与xj之间的流形上的线段长度定义如下[15]:

L(xi,xj)=ρdl(xi,xj)-1

(12)

式中,dl(xi,xj)为xi与xj之间的欧氏距离,ρ>1为伸缩因子,此处可取e3。

将数据点xi与xj看作是图G=(V,E)的顶点,令p={p1,p2,…pl}∈V表示图上一条连接点p1与pl的路径,其中边(pk,pk+1)∈E,1≤k≤l-1。令Pij表示连接数据xi与xj的所有路径集合,则xi与xj之间的流形距离定义如下[15]

(13)

式中,L(a,b)表示两点间流形上的线段长度。

由流形距离的定义可以看出,它不像欧氏距离直接计算两点间的空间距离,而是首先将数据点作为图的顶点,将近邻点连线作为图的边,然后从起点开始搜索最短边来寻找下一个最近邻点直至终点为止,最后计算所有最短边流形上的线段长度并加和便得到流形距离。收缩因子使得流形距离相比欧氏距离,放大了位于不同流形的点间距离,缩小了相同流形内的点间距离,如图1所示。

表1 流形距离

a与b之间的流形距离D(a,b)为0.872 4,a与c之间的流形距离D(a,c)为a至c共16个最短边的集合(最短边流形距离见表1),其大小为0.106 1。此时,流形距离可以正确衡量数据点间相似性。

综上所述,M-CFSFDP算法首先计算数据点之间的流形距离,然后在流形距离的基础上计算所有数据点的ρi和δi,再然后建立ρ-δ决策图来搜索聚类中心,最后指定剩余数据点类别,获得聚类结果。

下面给出M-CFSFDP的算法流程:

输入:待聚类数据集

输出:聚类结果

1) 数据标准化。采用min-max标准化将各维数据映射到[0,1]之间。

2) 计算流形距离。首先计算数据点之间的欧式距离;然后指定近邻点个数n,一般可取3～5;再然后将每个数据点与其近邻点连接生成图;最后依据(12)～(13)式计算各数据点之间的流形距离。

3) 求取截断距离。依据(11)式计算信息熵H,取H最小时对应的影响因子σ为截断距离dc。

4) 计算局部密度ρi和高密度近邻点距离δi。计算方法依据公式(7)～(9)。

5) 寻找聚类中心。构建ρ-δ决策图来寻找聚类中心。

6) 非中心数据点归类。归类原则为:对于数据点xi,寻找高于该点局部密度的所有点,选择其中距该点最近的点xj,则xi与xj的类别一致。

3 仿真实验

3.1 人工数据集和UCI数据集聚类

本文同时利用CFSFDP算法和M-CFSFDP算法,来对人工数据集和UCI标准数据库中的数据集进行聚类实验,以期验证M-CFSFDP算法的正确有效,且聚类结果优于CFSFDP算法。实验数据基本信息如表2所示。图2～5是人工数据集的仿真结果。

表2 人工数据集和UCI数据集信息

图2 threecircles数据集聚类结果 图3 lineblobs数据集聚类结果

图4 jain数据集聚类结果 图5 spiral数据集聚类结果

图2～4表示4种人工数据集聚类结果,其中a)、b)分别表示CFSFDP算法和M-CFSFDP算法的ρ-δ决策图,用于确定聚类中心;c)、d)分别表示2种算法的聚类结果。对于图2数据集,图2a)显示CFSFDP算法只能寻找到一个正确的聚类中心,无法准确寻找到其余2个聚类中心,从而导致图2c)聚类结果完全错误;而图2b)显示M-CFSFDP算法可以准确搜寻3个聚类中心,图2d)聚类结果也将所有数据正确分为3类。对于图3、4数据集,虽然CFSFDP算法可以找到聚类中心,然而由于欧氏距离无法正确衡量数据点间的相似性,使得数据点的ρi和δi计算结果出现偏差,从而导致部分数据点的聚类错误,图3c)和图4c)都显示有数据点被错分。而流形距离可以正确衡量数据点间的相似性,故图3d)和图4d)中M-CFSFDP算法聚类结果未出现错分数据点。对于图5数据集,决策图与聚类结果表明,CFSFDP能够正确聚类时,M-CFSFDP也能够正确聚类。此外,对比上述所有数据集的决策图,发现M-CFSFDP能够更加明确地反映出聚类中心。正是由于流形距离的作用,使得M-CFSFDP搜索聚类中心的能力以及聚类效果都优于CFSFDP。

对于高维数据,本文以UCI数据库中的wine数据集为例,对比2种的聚类结果,如图6所示:

图6 wine数据集决策图

由图6a)可知,CFSFDP算法只能找到2个聚类中心,而图6b)中M-CFSFDP算法能够正确搜索3个聚类中心。而图中ρi很小而δi很大的点为单独孤立点,故不算作聚类中心。由于UCI数据集都为高维数据,聚类结果不便以图形表示,故表3给出聚类结果对比。由表3可知,对于iris数据集,M-CFSFDP能够显著提高聚类正确率;对于wine数据集,原方法甚至无法准确搜索聚类中心,确定聚类类别数。M-CFSFDP不但能准确搜索聚类中心,而且能够得到较为理想的聚类结果。对于seeds数据集,M-CFSFDP算法的聚类正确率仅是略微提高,这是由于数据集自身特性导致,说明该数据集仅通过CFSFDP算法就可以获得较高的聚类正确率。尽管聚类正确率提高有限,M-CFSFDP依然得到了较高的正确率,且优于CFSFDP算法。通过对人工数据集与UCI数据集的聚类仿真结果,可以充分证明M-CFSFDP算法的正确有效,且优于CFSFDP算法。

表3 UCI数据集聚类正确率

3.2 战场目标分群

在实际战场中,目标不断运动,其状态不断变化,从而导致目标之间所形成的空间群也会有所改变。一般来说,战场目标群体会存在诸如分裂、合并、单独成群等情况,这对于目标分群方法提出了更高的要求。下面通过一组战场我方目标的任务执行过程,来验证本文目标分群方法的正确性、有效性与可行性。

我方目标任务执行过程如图7所示:

图7 我方目标任务执行过程航迹

1) 起始时刻,目标1～3向北偏东30°方向飞行,执行侦查任务;目标4～7向北偏东60°方向飞行,执行侦查任务;目标8～10由北向西逆时针执行巡逻任务。

2) 当到达t1时刻,目标3,5,6接到突发任务安排,目标3与目标1,2分裂并单独成群,目标5,6与目标4,7分裂为2个空间群。其余目标仍执行原任务。

3) 当到达t2时刻,目标3与目标5,6合并成一个群,并开始向远处执行攻击任务。其余目标仍执行原任务。

下面应用本文提出的目标分群方法,来对上述任务执行过程中的所有目标进行分群。

1) 某时刻目标静态分群结果

t时刻目标状态信息如表4所示:

表4 状态信息表

其中,x,y,z表示目标的位置信息;φ表示目标的航迹方位角;V表示目标的速度。

t时刻目标分群结果如图8～10所示:

图8 t时刻目标分群结果(x-y视图) 图9 t时刻目标分群结果(x-z视图)图10 t时刻目标分群结果(三维视图)

由图8～10可知,t时刻目标被分为5个空间群,如表5:

表5 聚类结果表

由图8～10可知,如果仅仅参考目标之间的位置,可以明显得出目标1,2,目标4,7以及目标8,9,10各自成为一个空间群。然而,本文目标分群方法将目标3,5,6分为2个空间群,则证明了该方法在分群时能够结合目标各属性,切合实际地正确分群。图11表示各目标由起始时刻到达该时刻的航迹,航迹末端为该时刻目标所处位置。

图11 t时刻目标航迹

结合图11可知:目标1,2维持原航线,为空间群1;而目标3已经分裂出去并单独成群,为空间群4;目标4～7此时也已分裂为2个群体,目标5,6为空间群2,目标5,7为空间群4;目标8～10为空间群3。

(2)全时段目标分群结果

任务执行全时段目标分群结果如下所示:

图12 全时段目标分群结果

由图12可知,在起始时刻,目标1～3属于空间群1,目标4～7属于空间群2,目标8～10属于空间群3;经过一段时间后,目标3与目标1,2分裂并单独成群,为空间群4。目标4,7与目标5,6分裂,为空间群5;最后,目标3与目标4,7又合并成空间群4。

图13以全程航迹的形式表现了目标分群结果。上述分群结果与设计的任务执行过程吻合,并且对于目标分裂、合并以及单独成群等特殊情况都可以

正确分群,充分说明了本文目标分群方法对于动态分群的正确性与可行性。

图13 全时段目标分群航迹图

4 结 论

本文针对战场目标分群问题,提出了一种基于M-CFSFDP算法的目标分群方法。该方法利用流形距离替代欧氏距离以期正确衡量目标之间的相似度,并在此基础上对CFSFDP算法进行改进。通过对人工数据集和UCI数据集进行仿真,验证了M-CFSFDP算法搜索聚类中心与聚类效果均优于CFSFDP算法;同时应用该方法对战场目标进行静态与动态分群,仿真结果表明该方法能够在起始空间群数量未知的前提下,对具有高维属性的战场目标既可以进行某时刻的静态空间分群,又可以获得整个任务执行过程的正确分群结果。