斜齿轮修形对负载扭矩和啮合错位的敏感性

袁冰, 常山,2, 刘更, 刘岚, 常乐浩

(1.西北工业大学 陕西省机电传动与控制工程实验室, 陕西 西安 710072；2.中国船舶重工集团第七〇三研究所, 黑龙江 哈尔滨 150078;3.长安大学 道路施工技术与装备教育部重点实验室, 陕西 西安 710064)

齿轮传动系统的振动噪声一直是机械工程领域关注的热点问题。作为齿轮系统减振降噪的主要手段之一，齿面修形技术被广泛应用于齿轮的设计与制造，并得到了国内外科研人员深入广泛的研究。

早期的齿轮修形主要为齿廓修形并大多应用于直齿轮，其概念的提出可追溯到1938年[1]。经过数十年的研究与发展，目前直齿轮齿面修形的相关研究主要涉及齿廓修形直齿轮准静态接触分析[2]，降低传递误差幅值的直齿轮齿廓修形减振设计[3]，齿廓修形直齿轮系统动态特性分析及优化[4]。

不同于直齿轮，斜齿轮的接触线与齿轮轴线不平行，其齿面接触特性的计算为较复杂的三维接触问题。Conry和Seireg基于柔度矩阵法提出了考虑轮齿修形的圆柱齿轮齿面载荷分布计算方法[5]，并得到了其他学者的推广和发展[6]。基于TCA和LTCA技术，蒋进科等采用修形曲面叠加理论齿面构造斜齿轮对角修形齿面，以降低斜齿轮副扭转振动为优化目标，采用改进二阶震荡粒子群优化算法确定最佳修形参数[7]。Wang等采用切片法和能量法建立了考虑齿廓误差和齿面修形的斜齿轮啮合刚度和传递误差计算模型[8]。Maatar和Velex分析了齿廓修形和齿向修形斜齿轮系统的准静态和动态特性[9]。Bruyère等以准静态传递误差幅值最小为目标，推导了窄直斜齿轮齿廓修形最佳修形量和修形长度的解析表达式[10]。

综上所述，现有的斜齿轮系统相关研究大多着重于讨论恒定负载扭矩和理想啮合状况下的齿面修形问题。由于齿面修形的最佳修形参数和轮齿变形量紧密相关，而系统负载扭矩决定了轮齿变形量的大小。因此，在不同负载扭矩下的最佳修形参数也会有所不同。在实际工业应用中，尤其在汽车行业和船舶动力传动装置中，齿轮系统的负载会随着汽车档位或者船舶航行工况的变化而产生较大变化。与此同时，由于安装误差和系统变形等不可避免的因素，齿轮的实际啮合状况与理想状态也有较大差异。因此，考察修形齿轮系统在不同负载扭矩和非理想啮合状态下的减振效果具有重要的工程实际意义。

为此，本文设计了斜齿轮齿廓修形、齿向修形和对角修形3种修形齿面，结合齿面承载接触分析方法和齿轮-转子-轴承系统动力学模型分离出系统振动激振力，确定了设计负载扭矩和理想啮合状况下的最佳修形参数，考察了不同修形方式对齿面接触特性的影响，并着重对比分析了在多负载、不同啮合错位量和多转速工况下3种修形方式的减振效果，为进一步齿面修形稳健设计提供参考。

1 齿面修形设计

斜齿轮齿面修形方式主要有齿廓修形、对角修形和齿向修形等。其中，齿廓修形和对角修形可直接用来降低斜齿轮系统的振动，而齿向修形则多被用来改善齿面载荷分布。实际上，齿向修形对斜齿轮系统振动也有较大影响，合理的齿向修形也可以用来改善斜齿轮系统的动态性能。斜齿轮3种齿面修形如图1所示。

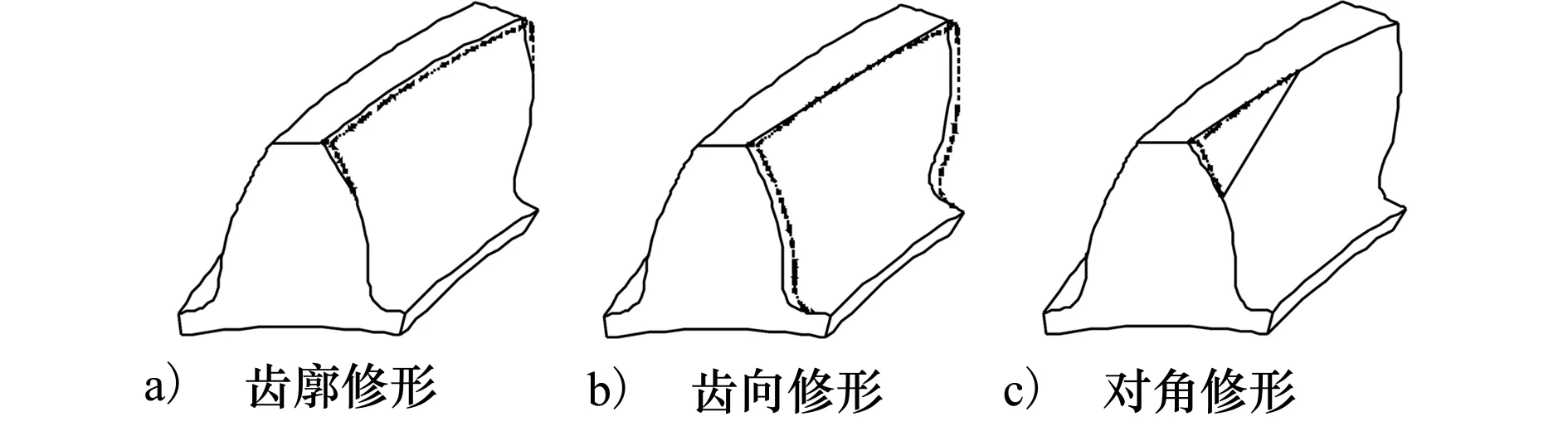
图1 齿面修形示意图

图1所示3种修形方式所构造的修形齿面均需要已知修形量、修形长度和修形曲线才能确定。其中，修形量和修形长度可通过优化来确定，而修形曲线类型必须进行预设定。修形曲线的通用表达式为

(1)

式中,emax为最大修形量,xi表示接触点i距离修形起始位置的距离,l表示修形长度。n表示修形曲线的类型,n=1时为直线修形,n=2时为二次抛物线修形。本文采用二次抛物线修形方式。

2 齿轮啮合错位

齿轮传动系统是一个较复杂的机械装置、轴承间隙、安装误差和制造误差等不可避免又难以测量的因素将会严重影响轮齿的啮合状况。当系统所受负载较大时,轴系的弯曲扭转变形,轴承变形和箱体变形同样会造成轮齿的实际啮合状况与理想状态有所不同。

文献[11]详细归纳总结了造成齿轮产生啮合错位的种种因素并指出齿轮的啮合错位主要可以分为3种类型,即中心距误差、垂直于啮合线方向的角度误差以及平行于啮合线方向的角度误差。平行于啮合线方向的角度误差直接影响齿面接触的法向间隙,其影响等效于齿轮螺旋线偏差,对齿面接触状态的影响最大。因此,本文啮合错位模型仅考虑平行于啮合线方向的角度误差,如图2所示。

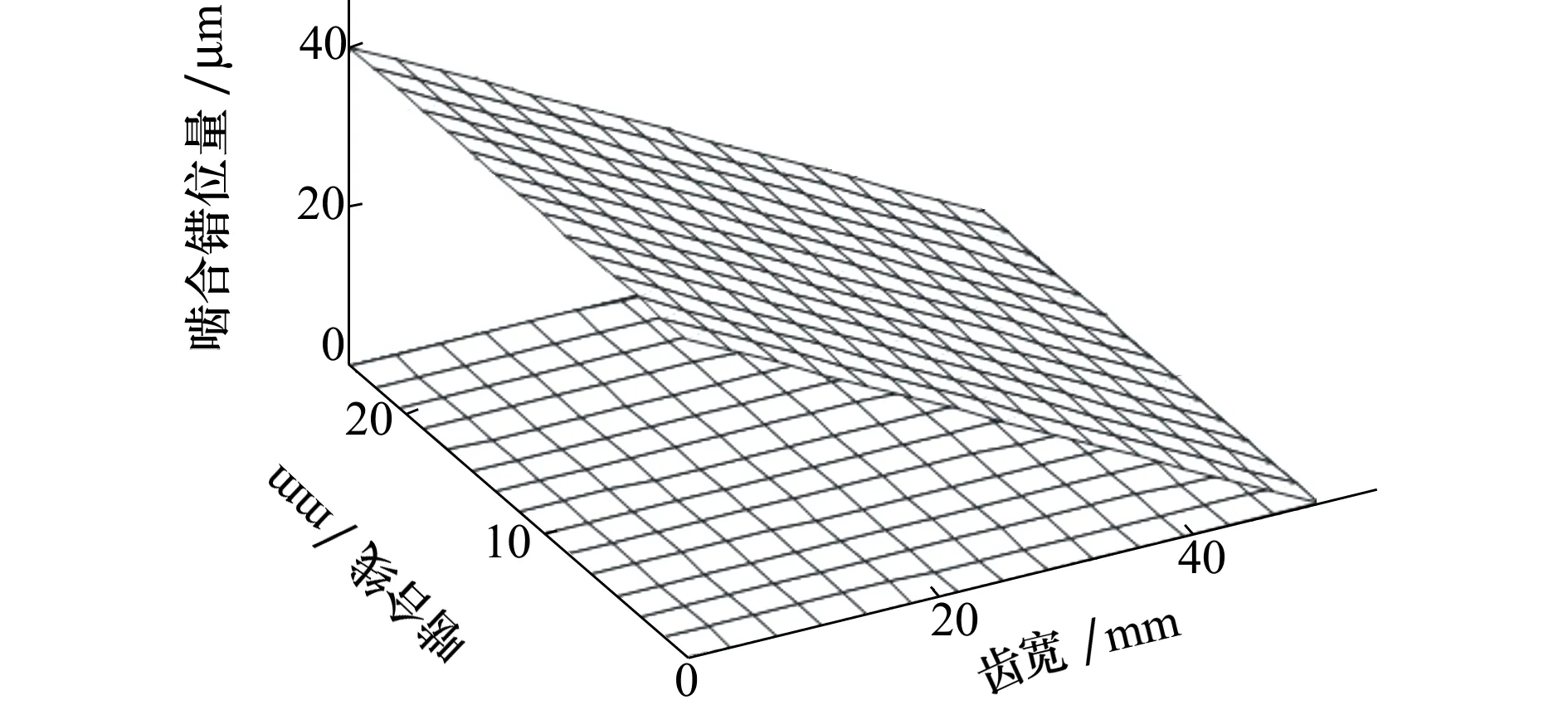
图2 啮合错位示意图

3 承载接触分析和振动激振力

3.1 时变啮合刚度和综合啮合误差

斜齿轮系统的准静态承载啮合过程可通过齿面承载接触分析模型模拟。根据齿轮啮合原理,确定齿轮啮合面并划分啮合位置,将各啮合位置的接触线离散为一系列接触点,从而将斜齿轮线接触问题转化为点接触问题。以总重合度为2～3的斜齿轮副为例,在一个啮合周期内,齿轮副处于双齿和三齿交替啮合状态,其啮合面划分及接触点布置如图3所示。

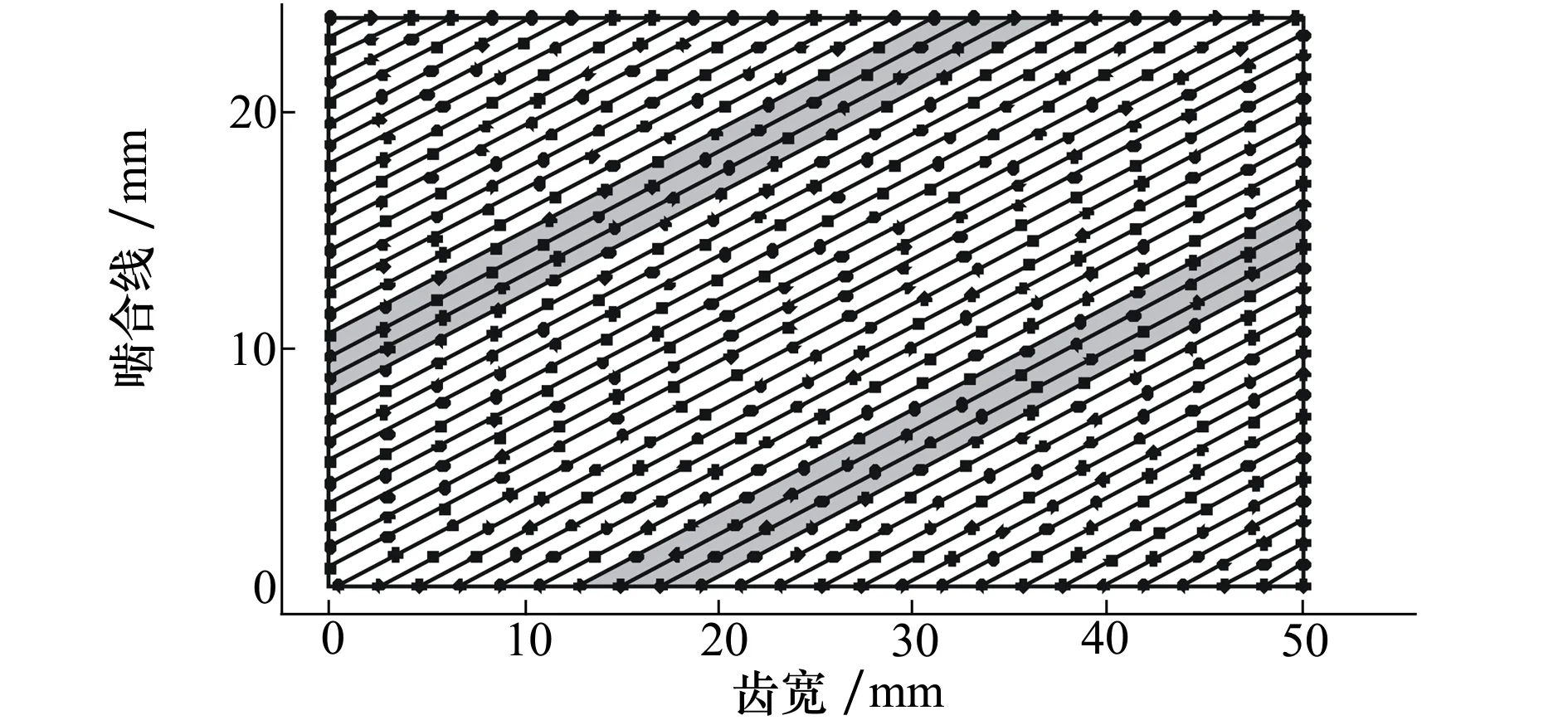
图3 斜齿轮副啮合面及接触点布置

基于有限元子结构法计算考察齿面法向宏观变形柔度矩阵,再通过二元插值得到各啮合位置的接触点法向宏观变形柔度矩阵。通过接触力学理论计算考察接触点的局部接触变形,根据齿轮各啮合位置接触点的变形协调条件,可建立齿面承载接触方程为

(2)

式中,λglobal为接触点宏观变形柔度矩阵,ulocal为接触点局部接触变形向量,F为接触点载荷向量,xs为静态传递误差,ε为接触点初始间隙向量,对于啮合齿轮副,各接触点的间隙量即为啮合齿面该位置的轮齿误差量或修形量,d为加载后接触点剩余间隙向量。通过迭代法求解该非线性方程组,可得到各啮合位置齿面载荷分布和静态传递误差,进而计算齿轮时变啮合刚度和综合啮合误差[12]。

3.2 振动激振力的确定

忽略箱体柔性和齿轮系统的耦合关系,则斜齿轮系统为齿轮-转子-轴承系统。考虑齿轮系统的功率流动方向以及质量和惯量呈空间分布的特点,基于有限元法基本思想,将系统分解为啮合单元,轴段单元和轴承单元3种基本单元。轴段单元采用2节点12自由度的空间Timoshenko梁模拟,轴承单元由轴承刚度和轴承阻尼组成,从而使轴段节点与箱体或基础相连接。

建立各单元的动力学模型之后,通过有限单元法可组装得到斜齿轮系统的广义有限元动力学模型[13]。系统运动微分方程可表示为

(3)

式中,X为系统广义坐标,MG为系统质量矩阵,CG为系统阻尼矩阵,KG为系统刚度矩阵,EG为系统综合啮合误差列向量,FG为外载荷列向量。

(3)式为参变微分方程组,通过近似变换[14],可近似改写为

(4)

式中,KG0为系统刚度均值矩阵,Xs(t)为系统静位移列向量。

(4)式右端项可改写为由均值项与波动项叠加形式

KG0Xs(t)=KG0Xs0+KG0ΔXs(t)

(5)

式中,将KG0ΔXs(t)定义为振动激振力,其决定了系统振动的剧烈程度。

(4)式为定常微分方程组,可通过傅里叶级数法快速求得系统振动响应稳态解[12]。

4 模型对比验证

齿面承载接触分析的计算结果为齿轮-转子-轴承系统提供动态激励,进而预测系统振动,而静态传递误差是齿面承载接触分析的直接计算结果,其波动量一直是国内外科研人员重点关注的参数之一。因此,为验证本文计算模型的正确性,分别计算了文献[15]中未修形和齿廓齿向均进行7.5 μm鼓形修形的斜齿轮副在不同负载扭矩下的静态传递误差波动量,并与文献[15]中的计算结果进行对比,如图4所示。结果表明:对于无修形和有修形斜齿轮副,本文方法的计算结果和文献的计算结果均具有较高的吻合度。因此,本文方法可以用来计算无误差和有误差的斜齿轮副的齿面承载接触特性。

图4 不同负载扭矩下静态传递误差波动量对比

5 算例分析

5.1 算例描述

图5所示为斜齿轮-转子-轴承系统示意图,系统由2根阶梯轴,1对斜齿轮副和2对轴承组成,功率从轴1左端输入,由轴2右端输出。齿轮基本参数如表1所示,轴系基本参数如表2所示。

图5 斜齿轮-转子-轴承系统

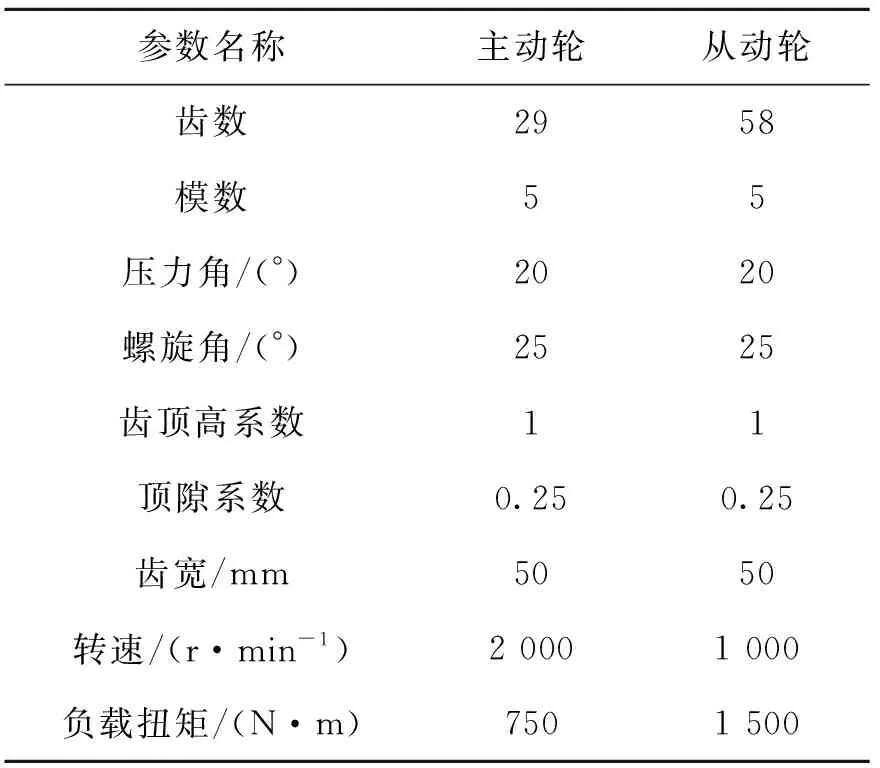
参数名称主动轮从动轮 齿数2958 模数55 压力角/(°)2020 螺旋角/(°)2525 齿顶高系数11 顶隙系数0.250.25 齿宽/mm5050 转速/(r·min-1)2 0001 000 负载扭矩/(N·m)7501 500

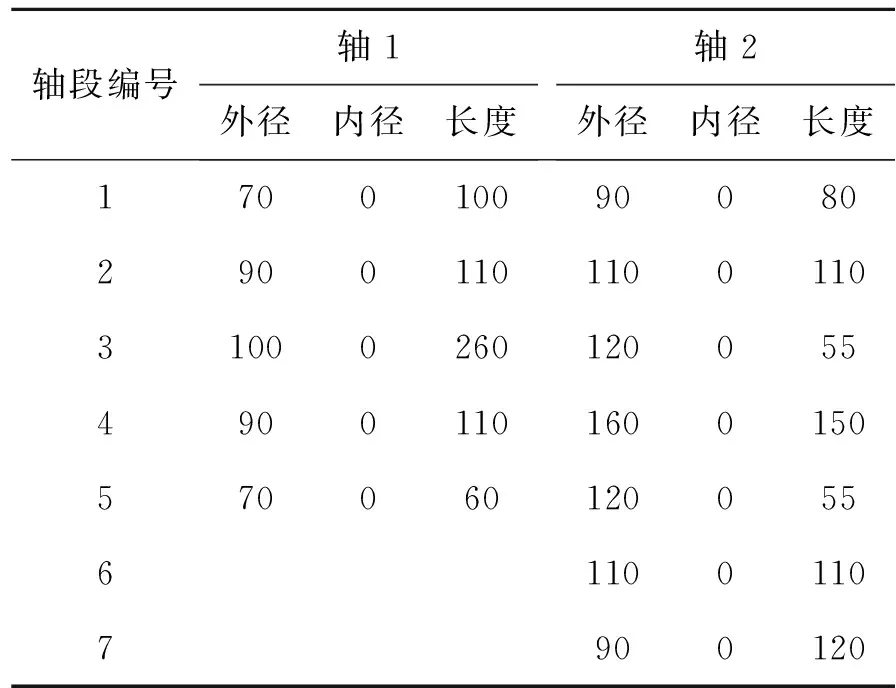
表2 轴系参数 mm

根据轴段结构,将轴1和轴2均离散为13个轴段单元,共26个轴段单元。有限元节点从轴1左端开始编号,在轴2右端终止编号,共28个节点,168个自由度。轴承1～4分别位于4,12,17和25号节点,主动轮和从动轮分别位于8和21号节点处,通过斜齿轮副时变啮合刚度和综合啮合误差相连接。2和27号节点分别为功率输入节点和功率输出节点。

5.2 最佳修形参数

本文在3.2节确定了决定系统振动的振动激振力表达式，其由齿轮时变啮合刚度和静态传递误差波动量的乘积决定。因此，最佳修形参数的确定实际上是求解以振动激振力波动量最小为目标的数学规划问题，即在修形参数的变化范围内寻求使振动激振力波动量最小的最优解。

由于振动激振力采用齿面承载接触分析方法计算且计算效率较高，同时为更直观地观察修形参数变化对目标函数的影响，本文采用直接扫略计算的方法确定设计负载扭矩和理想啮合状况下的最佳修形参数。将修形长度搜索区间均匀离散化，以斜齿轮啮入位置综合变形量的两倍作为修形量的上边界，修形量以1 μm为步长进行二维扫略计算，可得到齿廓修形、齿向修形和对角修形修形参数对振动激振力波动量的影响。可以发现，在3种修形方式相应的云图中，均存在一条窄带区域使系统振动激振力波动量降至200 N以下。限于篇幅，仅给出振动激振力波动量随齿廓修形参数的变化图，如图6所示。可得到齿廓修形最佳修形量为15 μm，最佳修形长度为11.97 mm，齿向修形最佳修形量为13 μm，最佳修形长度为21 mm，对角修形最佳修形量为10 μm，最佳修形长度为17.09 mm。

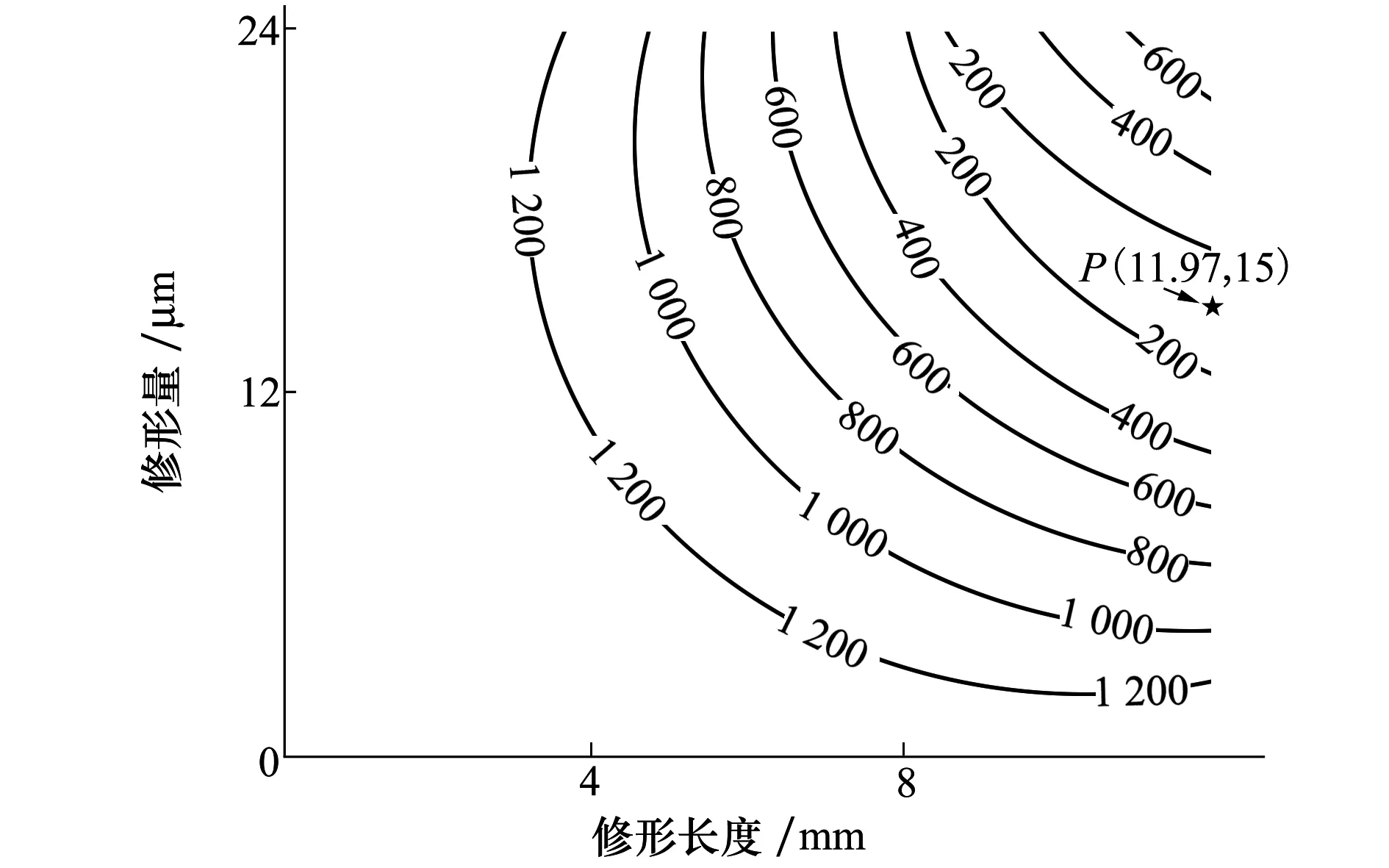
图6 齿廓修形参数对振动激振力波动量的影响

5.3 修形对齿面接触的影响

在设计负载扭矩和理想啮合状况下，齿廓修形、齿向修形和对角修形对斜齿轮时变啮合刚度的影响如图 7所示。可以看出，齿廓修形和齿向修形均使斜齿轮啮合刚度明显降低，这是由于齿廓修形最大修形量位于轮齿的齿顶和齿根，齿向修形最大修形量位于齿宽方向的两端，轮齿受载后齿面局部区域并不参与接触。而对角修形的最大修形量位于斜齿轮的啮入和啮出位置，轮齿受载后处于全齿面接触状态。

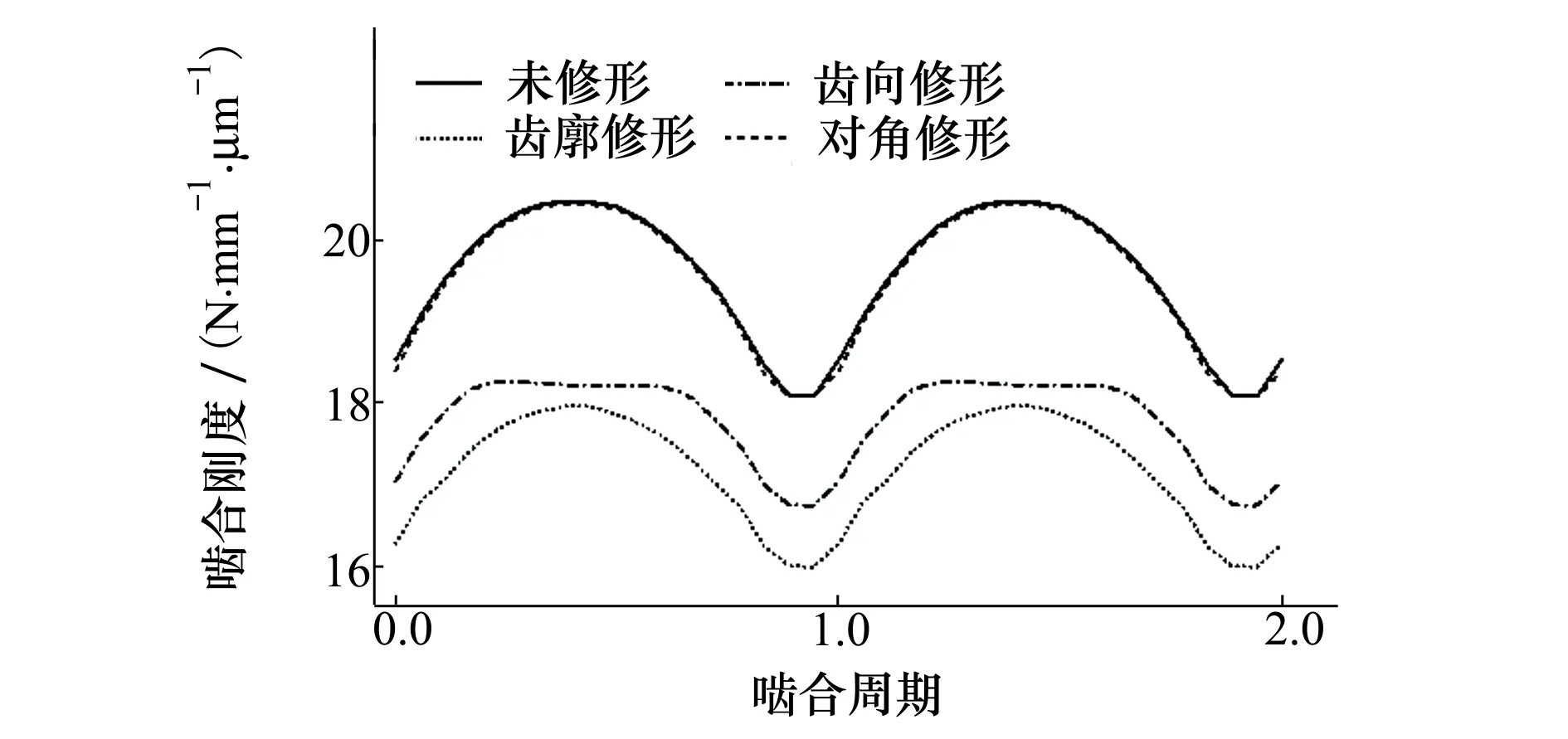
图7 不同修形方式下时变啮合刚度

在设计负载扭矩和理想啮合状况下，3种修形方式对斜齿轮静态传递误差和综合啮合误差的影响分别如图8和图9所示。可以看出，3种修形方式均使静态传递误差波动量明显降低，而齿廓修形斜齿轮传递误差均值最大，齿向修形次之，对角修形最小且在部分啮合位置与理想齿轮非常接近。综合啮合误差为考虑斜齿轮多对轮齿交替啮合时的齿面误差实际作用量，可以发现，3种修形方式相应的综合啮合误差曲线与时变啮合刚度曲线形状非常接近，同时相应的齿轮综合啮合误差均明显小于齿轮的最大修形量。

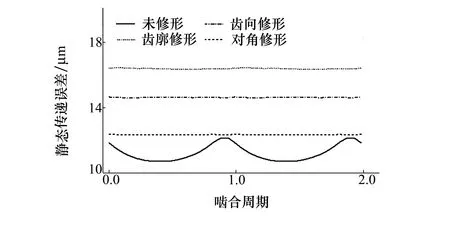
图8 不同修形方式下静态传递误差

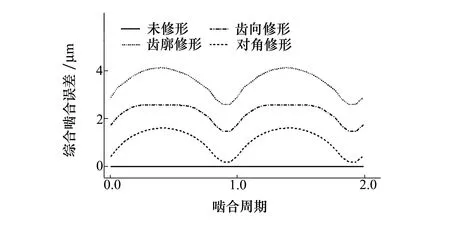
图9 不同修形方式下综合啮合误差

5.4 修形对负载扭矩的敏感性

本节采用5.2节所得最佳修形参数对斜齿轮进行修形，通过考察修形斜齿轮系统在7种不同的负载扭矩工况下的系统振动激振力和动态响应来研究修形对负载扭矩的敏感性。负载扭矩分别为250 N·m,500 N·m,1 000 N·m,1 500 N·m,2 000 N·m,2 500 N·m和3 000 N·m时，系统振动激振力波动量如图10所示。

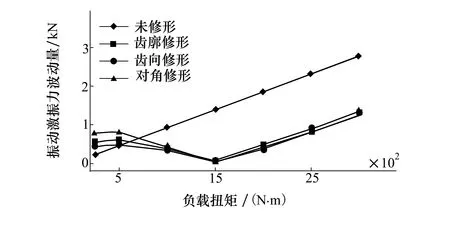
图10 不同负载扭矩下振动激振力波动量

可以看出，未修形齿轮系统的振动激振力波动量随着负载扭矩的增大呈线性增加趋势。在额定负载扭矩1 500 N·m工况下，3种修形方式的系统振动激振力波动量均达到最小且非常接近。随着负载扭矩的减小，振动激振力呈现增大趋势，当负载扭矩小于500 N·m时，3种修形方式的振动激振力波动量将大于未修形齿轮系统。当负载扭矩大于1 500 N·m时，修形齿轮系统的振动激振力波动量呈线性增加趋势，但均明显小于未修形齿轮系统。当负载扭矩达到2 500 N·m时，与未修形齿轮系统相比，齿廓修形、齿向修形和对角修形齿轮系统的振动激振力波动量分别下降了61.6%，65.3%和61.5%。

负载扭矩为500 N·m,1 500 N·m和2 500 N·m时，不同转速下的动态传递误差均方根值依次如图11～图13所示。

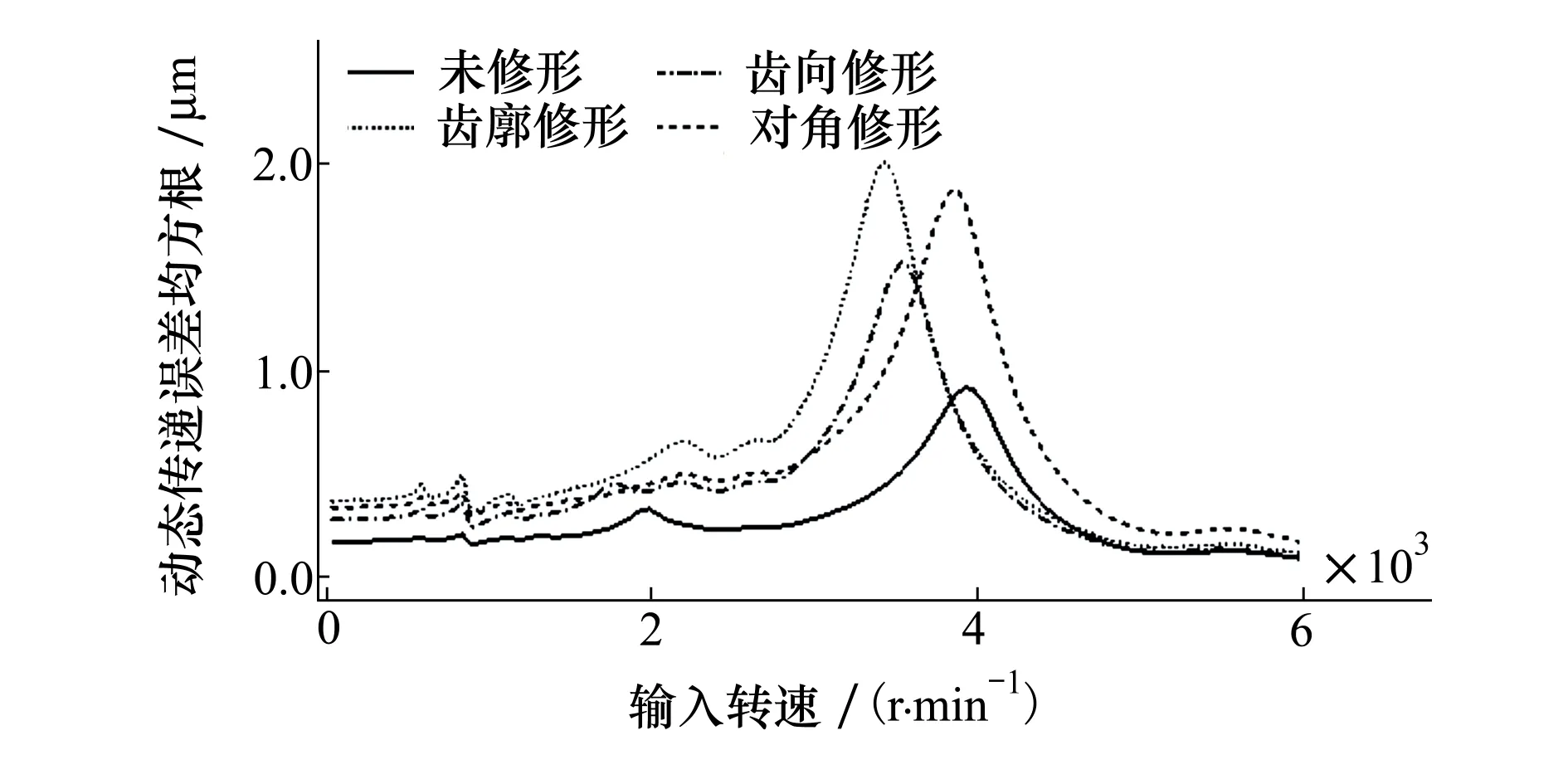
图11 负载扭矩为500 N·m时动态传递误差均方根

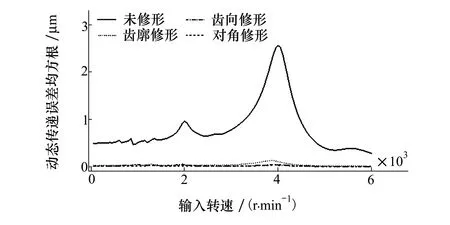
图12 负载扭矩为1 500 N·m时动态传递误差均方根

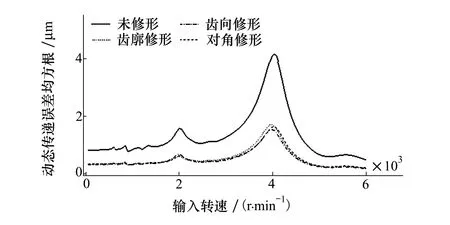
图13 负载扭矩为2 500 N·m时动态传递误差均方根

可以发现，当负载扭矩为500 N·m时，在大多数转速下，3种修形齿轮系统振动均大于理想齿轮，这是由于修形引入了过大的主动误差激励。齿廓修形和齿向修形斜齿轮系统共振转速明显降低，这是由于轻载时这2种修形使齿面实际接触的区域减小过多而导致啮合刚度均值下降过多造成的。当负载扭矩为1 500 N·m时，不同转速下的3种修形齿轮系统振动均明显小于理想齿轮系统，在额定转速下，动态传递误差均方根值分别降低了94.8%,96.5%和97.4%。当齿轮系统处于重载工况下，即负载扭矩为2 500 N·m时，3种修形方式均仍旧表现出较

好的减振效果，动态传递误差均方根值分别降低了60.1%,61.7%和61.0%。

5.5 修形对啮合错位的敏感性

本节采用5.2节所得最佳修形参数对斜齿轮进行修形，通过考察修形斜齿轮系统在7种不同的啮合错位工况下的系统振动激振力和动态响应来研究修形对啮合错位的敏感性。啮合错位分别为0 μm,10 μm,20 μm,30 μm,40 μm,50 μm和60μm时，系统振动激振力波动量如图14所示。

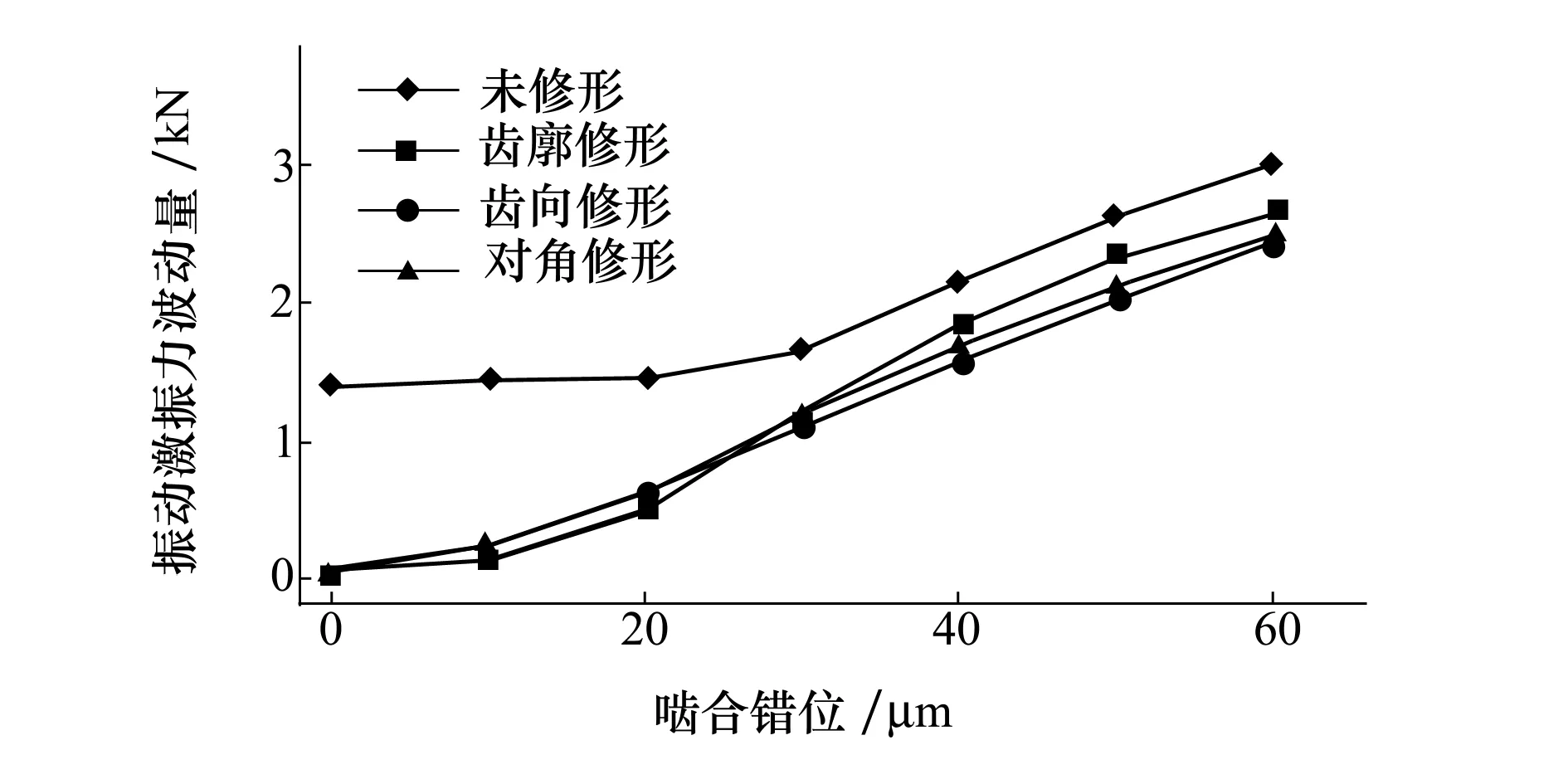
图14 不同啮合错位量下振动激振力波动量

可以看出，当啮合错位量小于30 μm时，理想齿轮的振动激振力波动量变化较小，当啮合错位量大于30 μm时，其振动激振力波动量呈近似线性增加趋势。随着啮合错位量的增加，3种修形齿轮系统的振动激振力均近似线性增加。当啮合错位量为30 μm时，3种修形方式使系统振动激振力仅降低了28.9%，33.3%和29.4%。

啮合错位量为10 μm,30 μm和50 μm时，不同转速下的动态传递误差均方根值分别如图15～图17所示。

图15 啮合错位为10 μm时动态传递误差均方根 图16 啮合错位为30 μm时动态传递误差均方根 图17 啮合错位为50 μm时动态传递误差均方根

可以看出，当啮合错位量为10 μm时，3种修形方式均有较好的减振效果，在额定转速下，动态传递误差均方根值分别降低了88.7%,80.6%和83.9%。当啮合错位量为30 μm时，系统共振转速略有降低，3种修形齿轮系统振动均显著增大，仅略小于理想齿轮，在额定转速下，3种修形方式使动态传递误差均方根值分别仅降低了26.1%,31.6%和23.4%。当啮合错位量为50 μm时，系统共振转速进一步降低，齿廓修形和对角修形几乎不再有减振效果，在部分转速下，3种修形齿轮系统的振动与理想齿轮系统基本相等。

6 结 论

1) 基于齿面承载接触分析方法和齿轮-转子-轴承系统动力学模型，通过近似变换分离出了系统振动激振力。以振动激振力波动量最小为目标，通过绘制振动激振力波动量随修形量和修形长度的变化图，确定了设计负载扭矩和理想啮合状况下齿廓修形、齿向修形和对角修形的最佳修形参数。

2) 3种修形方式对齿面接触的影响差别较大。齿廓修形和齿向修形均会显著降低齿轮啮合刚度，而对角修形斜齿轮啮合刚度与未修形齿轮副非常接近。3种修形方式均使静态传递误差波动量显著减小，齿廓修形引入齿面综合啮合误差最大，齿向修形次之，对角修形最小。

3) 在设计负载扭矩和理想啮合状况下，3种修形方式均可显著降低斜齿轮系统动态传递误差均方根值。当负载扭矩大于设计扭矩时，3种修形方式均依旧表现出较好的减振效果。而当负载扭矩过小时，由于齿面修形引入相对过大的主动误差激励，修形齿轮系统的振动将大于未修形齿轮系统，且系统共振转速降低。随着啮合错位量的增加，3种修形方式的减振效果均逐步下降，直至不再具有减振效果，同时，系统共振转速降低。