考虑弯扭耦合效应的复合材料叶片铺层优化方法

张龙, 贾普荣, 王波, 徐斌

(1.西北工业大学 力学与土木建筑学院, 陕西 西安 710072; 2.西北工业大学 航空学院, 陕西 西安 710072)

风扇叶片是航空发动机、船用推进器以及风力发电机的重要组成部分[1-3]。传统风扇叶片是由金属材料制成，但对于发动机而言，减轻结构重量能有效提高发动机的性能，因此为满足日益增长的这一需求，采用复合材料替换传统金属材料是一种有效且可行的途径[4-5]。相比于金属材料，复合材料具有质量轻、比模量高、比强度高、耐腐蚀、耐疲劳以及抗振动等优点。同时复合材料具有各向异性这一特点，在受载时会产生拉伸、剪切、弯曲和扭转之间互相的耦合效应，这使得复合材料结构设计具有更多灵活性，但也使设计更加复杂[6]。

由于传统金属叶片模量高，受载时叶片变形较小，因此在设计过程中一般忽略叶片气动外形的变化对结构性能的影响[7]。然而复合材料叶片的变形较大，并且不同铺层方案的变形差异也较大，过大的变形会导致叶片不再满足气动弹性外形的设计，进而导致叶片结构效率下降。因此在铺层设计时必须考虑变形对叶片气动弹性结构效率的影响[8]。周邢银等人对复合材料悬臂梁不同区域上的弯扭耦合效应对结构变形的影响进行了研究[9]。彭峰和Xiao等人分别对船用复合材料叶片和发动机叶片进行了研究，结果表明铺层角度、铺层厚度、铺层顺序对复合材料叶片结构的性能有显著影响[10-11]。Abdul等人通过不同铺层顺序的试验与仿真研究表明铺层顺序对叶片结构变形的影响很大[12]。同时相比于弯曲变形，叶片的扭转变形会改变叶片的攻角，而攻角的改变会显著降低叶片结构的效率[13]。为了提高叶片结构效率，必须减小叶片气动外形的改变，尤其是减小扭转变形。因此可以利用复合材料对称层合板结构中的弯扭耦合效应，通过调整铺层角度和铺层顺序，使结构中由弯矩通过耦合效应产生的扭转变形，与扭矩产生的扭转变形相互抵消，减小叶片的整体扭转变形，从而提高叶片气动弹性结构的效率[14-15]，达到铺层优化设计的目的。

本文基于经典层合板理论，提出了2个分析参数：刚度权值和载荷系数。通过设计弯扭耦合试验，研究了2个分析参数对弯扭耦合效应的影响，并结合有限元模拟对试验数据与理论结果进行了对比验证。进一步采用刚度权值和载荷系数对弯扭耦合效应进行了定量分析，将求解满足最小曲率目标函数时的最优铺层顺序转化为求解最优刚度权值，得到随载荷系数变化的最优刚度权值曲线。在给定任意弯扭载荷系数下，通过对最优刚度权值曲线的逆向计算，能够直接得到满足结构设计条件的最优铺层顺序，为复合材料叶片的铺层优化设计提供了参考和依据。

1 刚度权值和载荷系数的定义

1.1 刚度权值

为了分析对称层合板结构中相同铺层角度所在铺层位置对弯扭耦合效应的影响，基于经典层合板理论(CLT)，将面内刚度矩阵A和弯曲刚度矩阵D中相同的铺层角度进行合并,刚度矩阵表述如下:

(1)

式中，H为层合板总厚度,r为铺层角度种类的数量;i为铺层角度的编号,Qi为对应角度的偏轴刚度矩阵,αi和δi分别为该角度的面内和弯曲刚度权值,由公式(2)给出:

(2)

式中，mi为第i个角度的铺层数量,hi, t和hi, t-1分别为该角度下第t层的上下表面的Z坐标值。根据公式(2)的定义,αi与铺层含量意义相同,且αi和δi满足如下关系

(3)

1.2 载荷系数

为了分析不同载荷比例对耦合效应的影响,采用单位化对载荷进行变量代换,如公式(4)所示:

(4)

由此分别引入了体现铺层因素的分析变量:刚度权值α和δ,以及体现载荷因素的分析变量:比例系数ω。

2 试验与有限元模拟分析研究

2.1 弯扭耦合试验方案

图1为弯扭耦合试验加载方式示意图。图2为复合材料试件尺寸示意图。如图所示,通过在复合材料悬臂板加载端5个不同位置施加载荷分别为LN2,LN1,P0,LP1和LP2。实现扭矩由负到正的5种弯扭载荷比例,试验采用Instron1196电子万能试验机加载,试验速度为2 mm/min,当载荷达到60 N时,结束试验,保存数据。层合板选用M40J/CYCOM970高模量碳纤维复合材料,单层厚度0.125 mm,其单层属性见表1。

图1 试验加载方式示意图

图2 复合材料试件尺寸示意图(单位: mm)

E11/GPaE22=E33/GPaν12=v13ν23G12=G13/GPaG23/GPa179.1111.320.2540.455.262.76

表2为4种试件铺层顺序和对应铺层角度的δ。通过改变试件铺层顺序,实现δ的变化。在设计试件偏轴铺层角度时,为提高试验数据的可分析性,即在改变ω和δ时,提高曲率和扭率的变化量,应选择耦合效应较强的偏轴角度,同时考虑偏轴角度铺设的难易,偏轴角度以整数为宜,最终根据本文所用复合材料属性,选择30°作为偏轴铺层角度。

表2 试件铺层顺序和弯曲刚度权值δ

2.2 有限元分析模型

由于试验只能通过计算应变得到测点曲率,无法测得内力矩,因此不能直接对CLT理论进行计算验证。通过引入有限元(FEA)仿真计算,可以同时得到测点曲率和内力矩。通过对比试验与FEA的曲率数据,验证FEA的计算结果的正确性。再将试验曲率通过CLT理论计算得到的内力矩与FEA的内力矩进行对比分析,并以此来验证采用CLT理论对弯扭耦合效应进行分析计算是否可行。

本文采用ABAQUS商业有限元件对试验进行仿真模拟。模型尺寸和加载方式与图2、图1一致,材料属性和铺层顺序与表1、表2一致,采用C3D20单元,单元数为720 000。模型边界条件及加载方式如表3所示,均与试验条件尽可能保持一致。

表3 有限元模型边界条件及加载方式

2.3 试验与有限元结果对比分析

图3为4种试件试验和FEA的曲率κ-加载点曲线。结合表2中的权值与图中曲线可以看出:

1) 对比4种试件在P0纯弯曲加载时,随δ0增大,|κx|和|κy|减小;随|δ30-δ-30|增大,|κxy|增大;在δ30-δ-30>0的ABD型中κxy<0,反之在δ30-δ-30<0的C型中κxy>0。

2) 在δ30-δ-30>0的ABD型中,随Mxy增大κx减小,反之在δ30-δ-30<0的C型中κx增大,随|δ30-δ-30|增大,κx和κxy的斜率增大。

3) 对应5种不同弯扭载荷比例时,|κxy|最小值对应不同的铺层顺序。A型和B型|κxy|最小值对应在LP2加载点,其中A型|κxy|更小,C型和D型|κxy|最小值分别对应LN1和LP1加载点。

从以上分析可以发现,①δ0控制抗弯曲性能;②|δ30-δ-30|的大小控制耦合效应的强弱,δ30-δ-30的正负控制耦合效应的正负。③在不同弯扭载荷比例下,最小|κxy|对应的铺层也不相同。由此可将非连续的铺层顺序转化为连续的刚度权值,对复合材料弯扭耦合效应进行定量分析和研究。

图3 4种试件试验和有限元的曲率κ-加载点曲线

图4为4种试件试验和FEA的力矩M-加载点曲线,其中试验的合内力矩M是由试验的曲率数据通过CLT理论计算得到的。从图中可以看出4种试件的受载情况基本一致。对4种试件的M求平均并计算得到平均ω,如表4所示。结合表4可以看出,在5种加载方式下:①Mx数值最大,且大小基本相同;②My数值很小,几乎为0;③在P0加载点下,力矩Mxy几乎为0,基本为纯弯曲状态;加载点由LN2至LP2,Mxy由负变正。

图4 4种试件试验和有限元的力矩M-加载点曲线

Test/FEAωxωyωxyLN20.094/0.0920.987/0.9861.093/1.091 LN10.045/0.0460.995/0.9931.045/1.046 P00.002/0.0040.997/0.9961.000/1.000 LP10.050/0.0480.996/0.9940.950/0.952 LP20.096/0.0940.987/0.9860.905/0.906

为比较试验和FEA 2组曲线的数据误差,采用积分绝对值误差准则(IAE)对数据进行分析,计算方法如公式(5)所示,式中DTest表示试验数据,DFEA表示有限元数据,n为数据的数量。误差计算结果如表5所示。

(5)

从表5中可以看出,试验与FEA的κx和κy误差较小,κxy误差相对较大,这可能是由于κxy是通过应变转轴公式计算得到,误差被进一步放大。表5中试验和FEA的Mx和Mxy误差相对较小,My的误差很大,但从图4b)中可以看出My基本接近0,因此数据差异可能不大,但得到的误差会较大。通过误差分析可以看出,试验与FEA的曲率数据基本一致,并且通过CLT理论计算得到的力矩与有限元仿真计算得到的力矩也相对一致。因此间接通过FEA模拟对CLT理论与试验数据进行了验证,可认为采用CLT理论对弯扭耦合效应的分析是可行的。

3 弯曲刚度权值的最优路径研究

3.1 问题描述

本文以工程中常用的由0°,90°,±45°组成的对称层合板为例,以优先满足min(|κxy|),其次满足min(|κx|)为目标函数,进一步定量研究在不同ω下,δ的比例关系。由公式(1)可得层合板弯曲刚度矩阵如下

(6)

式中,Qi为i=0°,90°,±45°时单层板的偏轴刚度矩阵。根据试验分析结果,取My=0对问题进行简化,由公式(4)可得公式(7),独立载荷因子剩下ωx,简记为ω。

(7)

当铺层角度确定后,κx和κxy分别是关于δ和ω的函数。根据对称性分析可知,将ω最优铺层中的±θ°层的角度互换可得-ω的最优铺层。因此在公式(7)中只需讨论ω∈[0, 1]的情况。

为满足最小的|κx|和|κxy|条件,须满足δ-45取值最小,根据层合板铺层含量的约束,假设满足α0≥0.6,其余铺层角度含量α≥0.1时,根据公式(3)中条件,4个δ中只有3个相互独立,此时权值可行域满足如下关系:

(8)

根据公式(8)可知,δ的可行域如图5所示,其中可行域边界点的权值坐标如表6所示。

图5 权值δ的可行域

可行域边界点权值δ坐标δ0δ90F10.9730.025 F20.9730.001 F30.5100.001 F40.2160.295 F50.2160.488 F60.5100.488

3.2 权值最优路径的求解计算

本文采用Maple数学工程计算软件对所需求解的方程进行计算。令H3/12=1，对公式(6)进行简化，由此可得κx和κxy分别是关于δ和ω的函数κx(δ0,δ90,ω)和κxy(δ0,δ90,ω)。令κxy=0可得不同ω下δ关于κxy=0的等高曲线方程,如公式(9)所示

(9)

根据公式(9)作图可得等高曲线δ90-δ0,如图6所示。从图中可以看出,ω存在一个临界值ω1:当ω∈[0,ω1]时,存在等高曲线δ90-δ0使得κxy=0,当ω=ω1时,等高曲线δ90-δ0与可行域相交于点F4;将点F4的权值带入公式(9)可得ω1=0.144;当ω∈[ω1, 1]时,κxy恒大于0。

图6 不同ω下可行域上κxy=0的δ等高曲线δ90-δ0

1) 当ω∈[0,ω1]时:

求解公式(9)分别可得δ90和δ0的函数表达式:

δ90|κxy=0=f(δ0,ω),ω∈[0,ω1]

(10)

δ0|κxy=0=g(δ90,ω),ω∈[0,ω1]

(11)

将公式(10)带入κx(δ0,δ90,ω)可得:

κx|κxy=0=κx(δ0,f(δ0,ω),ω),ω∈[0,ω1]

(12)

根据公式(12)可得在满足κxy=0的条件下,κx-δ0关于ω的曲线族,如图7所示。结合图6与图7可知,当ω∈[0,ω1]时,部分等高曲线关于δ0分为上下2个部分,部分等高曲线只有上半部分。且δ0取最大值时κx取得最小值。

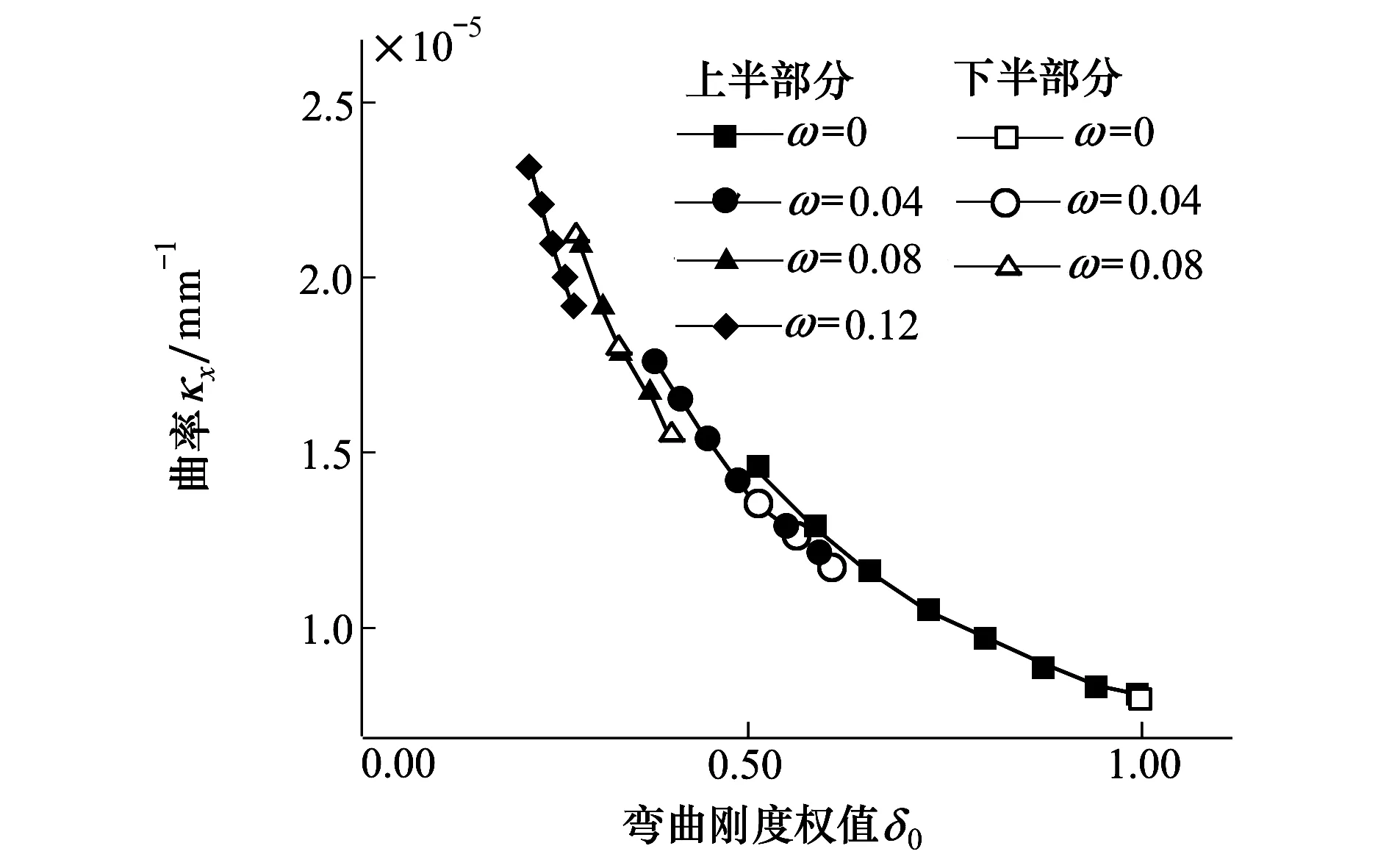
图7 不同ω下κxy=0时的κx-δ0曲线

为求得等高曲线上δ0的最大值,对图6进行分析可以看出,受可行域的约束,随ω增大,等高曲线上δ0的最大值被分为3个部分,分别在可行域边界F1F2F3,可行域内和可行域边界F3F4上。令方程(11)关于δ90求导为0,如公式(13)所示:

(13)

将方程(13)带入方程(11)并分别与F2F3和F3F4曲线方程联立求解,可得对应临界的ω分别为0.002和0.008。

分别对ω∈[0, 0.008],[0.008, 0.1]和[0.1,ω1]3个区间求解δ0的最大值,可得δ0(ω)函数方程。进一步带入公式(11)可得δ90(ω)函数方程,再根据公式(3)可得δ45(ω)函数方程。通过以上计算可得ω∈[0,ω1]时,满足κxy=0,且κx最小条件时,δ(ω)的最优路径。

2) 当∈[ω1, 1]时:

κxy恒大于0,根据图6可以看出,当ω=ω1时,κxy最小值在点F4。过点F4的κxy等高曲线方程如公式(14)所示

κxy(δ0,δ90,ω)=κxy|δ=F4,ω∈[ω1,1]

(14)

根据公式(14)可得不同ω下过边界点F4的κxy等高曲线族,如图8所示。从图中可以看出,存在一个临界值ω2,当ω∈[ω1,ω2]时,κxy最小值取在点F4处,当ω∈[ω2, 1]时,κxy最小值由点F4沿可行域边界向F3移动。

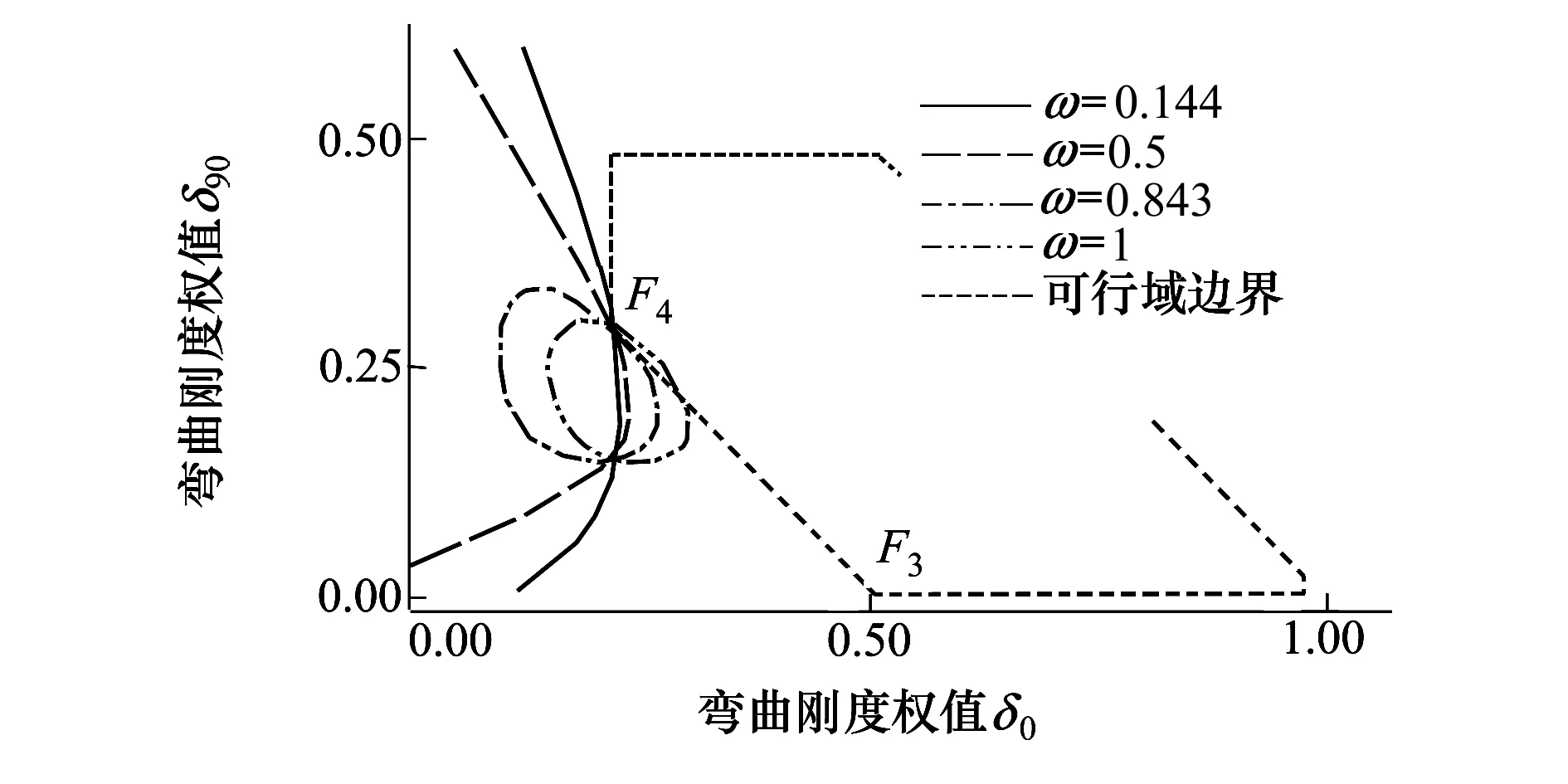
图8 不同ω下过边界点F4的κxy等高曲线族

将公式(8)中可行域边界F3F4带入κxy,并令κxy关于δ0求导为0,如公式(15)所示

(15)

将点F4的δ0带入公式(15)求解可得临界值ω2=0.843。对公式(15)求解可得ω∈[ω2, 1]范围内κxy最小值的δ0(ω)函数方程,带入公式(8)中可行域边界F3F4可得δ90(ω)函数方程,进一步可得δ45(ω)函数方程。

3.3 权值最优路径计算结果与分析

通过以上分析可得,在可行域约束下的δ最优路径,如图9所示。

图9 不同比例系数ω下可行域内权值δ的最优路径

图中虚线为可行域边界带有形状符号的曲线为对应不同ω时κxy=0的等高曲线,实曲线H1F2H2H3F4H4为整体δ最优路径δ90-δ0曲线。在该最优路径上,能够优先保证|κxy|最小,其次保证|κx|最小。由于受可行域边界的约束,δ最优路径被分为6个部分。当ω∈[0.008, 0.1]时,最优路径在可行域内的曲线H2H3上,当ω不在该范围时,最优路径在可行域的边界上。δ最优路径的拐点坐标与对应的ω如表7所示。

通过δ最优路径,可得δ(ω)曲线,如图10所示。结合表7与图10可以看出:

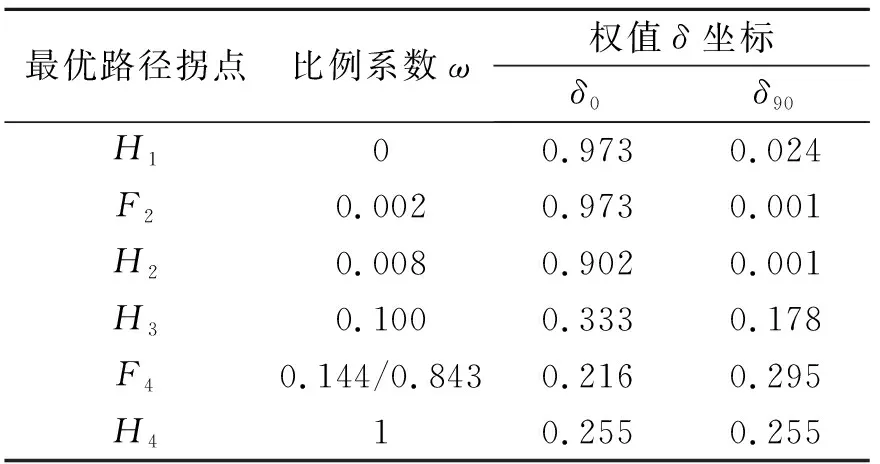
表7 权值δ最优路径拐点坐标与对应比例系数ω

图10 可行域上最优权值路径的δ-ω曲线

1) 当ω∈[0, 0.002]时,随ω增大,δ0不变,δ90减小,δ45增大。δ最优路径为可行域边界H1F1。

2) 当ω∈[0.002, 0.008]时,随ω增大,δ0减小,δ90不变,δ45增大。δ最优路径为可行域边界F1H2。

3) 当ω∈[0.008,ω1]时,随ω增大δ0减小,δ90和δ45增大,且δ45增幅大于δ90。以ω=0.1为分界,δ最优路径分为2个部分:可行域内的H2H3和可行域边界上的H3F4。

4) 当ω∈[ω1,ω2]时,随ω增大,δ0,δ90和δ45保持不变,δ最优路径停留在可行域边界点F4上。

5) 当ω∈[ω2, 1]时,随ω增大,δ0增大,δ90减

小,δ45保持不变,δ最优路径由点F4沿可行域边界向H4移动。

通过最优路径δ(ω),可以计算得到在最优路径上κ-ω曲线,如图11所示。从图中可以看出,在最优路径δ(ω)上:

1) 当ω∈[0,ω1]时,通过改变δ可以保证,随ω增大,κxy=0,κx取得最小值。

2) 当ω∈[ω1, 1]时,随ω增大,κxy开始增大,κx开始减小。

图11 可行域上最优权值路径的κ-ω曲线

3.4 权值最优路径的算例验证与讨论

本文以16层对称层合板为例,对最优路径δ(ω)进行验证。以试验中P0,LP1和LP2 3种情况的载荷因子为基础,分别选取ω=0,0.05,0.1以及ω1进行分析计算。根据铺层含量的约束关系可知4种角度的铺层数分别为0°铺层有10层,90°和±45°铺层各2层。

由于实际情况中δ的取值是在三维空间中的离散点(δ0,δ90,δ45)上,不一定刚好取在理论最优δ点上,因此实际最优δ点是离散的三维空间点中包围理论最优δ点最小六面体8个顶点中的1个。通过计算实际与理论δ最优点的距离可以计算得到六面体8个顶点的权值δ,从8种情况中选取满足最优条件的最优实际δ,即为所求最优实际最优解。

表8 对应比例系数ω下权值δ,曲率κ的理论与实际最优解及铺层顺序

表8为采用Maple编程计算得到对应ω的δ和κ的理论、实际最优解,及对应的实际铺层顺序。从表中可以看出,最优解的理论与实际的δ和κ非常接近。①当ω=0纯弯曲时,0°层在最外层,±45°层在最内层;②随ω增大,45°层最先移动到外层,90°和-45°层相继向外层移动。当ω=0.05时,δ45的实际值为0.330,已经达到实际的最大值,但仍小于δ45的理论值0.341,随ω增大,二者差异增大,κxy也开始增大。这是由于实际铺层的非连续性以及受到铺层含量的约束导致δ的实际最优值不能完全与理论最优值重合。

4 结 论

本文基于经典层合板理论提出了2个分析参数：①将非量化的铺层顺序转化为可量化分析的刚度权值；②将合内力矩转化为归一化的载荷系数。并通过弯扭耦合试验与有限元模拟讨论了2个分析参数对弯扭耦合效应的影响。

以弯曲刚度权值的可行域为约束条件,结构曲率最小为目标函数,对含有0°,90°,±45°的层合板进行了优化分析,得到了弯曲刚度权值的最优路径。受到可行域的限制,弯曲刚度权值最优路径被分成6个部分。①在前4个部分中,即ω∈[0,ω1]时,存在优化权值比例使得曲率κxy=0,|κx|取得最小值。②当ω∈[ω1, 1]时,受到可行域的限制,在弯曲刚度权值最优路径上,随ω增大,曲率κxy开始增大,κx开始减小。

根据本文提出的刚度权值最优路径,在给定任意的弯扭载荷条件下,可以得到对应的理论最优刚度权值,经过逆向计算可以得到实际最优铺层顺序。通过该方法能够快速有效地找到满足曲率设计目标的最优铺层顺序,能够对复合材料叶片弯扭耦合效应的优化设计提供一定的参考和依据。在本文的分析研究中,将叶片模型简化假设为层合板,忽略曲面叶形结构的影响,因此在后续的工作中需要进一步研究在曲面叶形结构上弯扭耦合效应的优化分析。