舰船空气流场数值模拟及特性分析

郭佳豪, 祝小平, 周洲, 许晓平

(1.西北工业大学 航空学院, 陕西 西安 710072; 2.西北工业大学 无人机特种技术重点实验室, 陕西 西安 710065)

舰船上复杂的气流直接影响舰载飞行器的正常起降,导致驾驶难度增加,严重时甚至威胁到驾驶员的生命,因此对舰船空气流场特性的研究有着重要意义。

风洞实验是舰船空气流场特性研究的有效手段。Zan等[1-2]通过油膜成像法及热线风速仪分别对简单护卫舰SFS 1∶60缩比模型与SFS2 1∶100缩比模型的流场进行了测量。Rajagopalan等[3]采用粒子图像测速法(particle image velocimetry,PIV)测量了两栖攻击舰LHA 1∶48缩比模型在不同风速和不同风向下的流场。国内方面,刘航等[4]在风洞中观测到了舰船飞行甲板上方流动强烈的随机性。赵维义等[5-6]均开展了舰船空气流场的PIV测量实验。但风洞实验存在周期长、成本高的缺点。

随着计算流体力学(CFD)技术的发展,数值模拟方法已广泛应用于舰船流场计算之中。Reddy等[7]基于结构网格定常计算,分析了简单护卫舰模型甲板上方不同位置的速度分布。Polsky等[8]对LHA进行了数值模拟,发现非定常取得的时均结果与实验数据更加符合,且舰船流场结构表现出雷诺数无关性。陆超等[9-10]通过对LHA缩比模型进行数值模拟,探讨了相似准数对舰面空气流场的影响,并对比了2种不同飞行甲板的流场特征。贲亮亮等[11]通过求解定常雷诺平均Navier-Stokes方程(RANS),分析了不同风向和风速下舰载机进舰轨迹上的速度分布特征,但由于舰船流场体现出非稳态特征,速度分布随着时间推进会产生较大的波动,定常计算并不能得到这种速度变化。郜冶等[12-14]则通过求解非定常雷诺平均Navier-Stokes方程(URANS)对不同风向下甲板涡结构进行了分析,并模拟了舰载机滑跃起飞过程中舰面流场变化,但其在验证数值方法时与实验数据对比仍有较大差距。上述研究大多采用RANS求解,但局限于RANS自身的数值耗散,对舰船流场非定常现象模拟及涡结构捕捉的精度有待进一步提高。而Forrest[15]和操戈等[16]通过模拟SFS2的流场,验证了分离涡模拟(detached eddy simulation,DES)捕捉舰船流场涡结构的能力。

本文将分别采用RANS与DES方法,对比其在舰船空气流场研究中的特点。并通过DES数值模拟方法分析航母空气流场的主要特征及复杂流动在舰载机进舰轨迹上引起的速度波动,以此探究舰载机的着舰环境。

1 DES模型简介

DES方法是将RANS与大涡模拟(large eddy simulation,LES)结合起来进行求解的一种混合方法[17-18]。其将RANS湍流模型中的长度尺度lR与LES长度尺度lL用新的长度尺度lD替换:

lD=min(lR,lL)

(1)

对于S-A湍流模型,长度尺度即距壁面的距离:

lR=d

(2)

k-ωSST湍流模型的长度尺度为:

(3)

β*为SST模型中的一个常数,k与ω分别为湍动能及湍流比耗散率。LES长度尺度为:

lL=CDESΔ

(4)

式中，Δ为局部网格尺度,是网格单元的三维尺寸的最大值;CDES为DES模型中的校准常数,取值为0.65。从lD的构造中可以看出,DES模型在近壁面区域采用传统RANS求解高频小尺度运动,在其余区域采用LES求解低频大尺度运动。

由于网格疏密程度的不同,LES计算可能在边界层中被激活,但LES求解边界层时需要相比RANS更大的网格密度。此时若被激活会导致求解中产生过小的湍流黏性,从而导致模化应力损耗(modeled stress depletion,MSD)的发生,致使网格诱导分离[19]。

为解决该问题,DES方法增加了避免在边界层中激活LES的延迟选项[19],采用新的长度尺度lN:

lN=lR-fdmax(0,lR-CDESΔ)

(5)

fd为延迟函数:

fd=1-tanh([8rd]3)

(6)

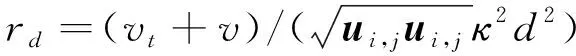
(7)

式中，vt为动涡黏性,v为分子黏性,ui,j为速度梯度,κ为Kármán常数,d为距壁面距离。当fd接近0时采用RANS求解,fd接近1时变为传统DES求解方法。本文采用增加延迟选项的DES方法。

2 几何模型及计算条件

2.1 计算模型与网格划分

采用简单护卫舰SFS2模型,该模型由标准的几何体组成,如图1所示。其船长l=138.684 m,船宽b=13.716 m,机库高h=6.096 m。计算采用结构网格。由于DES求解中局部网格尺度Δ取决于网格单元三维最大尺寸,因此对船体及周边区域网格划分时需保证3个方向网格尺度的统一。参考文献[15,20],保证舰船周围区域的目标网格尺度(Δ0)为:Δ0/b=0.05。对甲板上方这样的“重点关注区域”,网格加密处理,取Δ0/b=0.03,如图2所示。调整第一层网格距离,保证y+≈1,最终生成网格单元总量为486万。

图2 SFS2网格局部示意

2.2 计算条件

计算采用理想气体模型,计算高度为海平面,自由来流速度V0=20 m/s,来流方向沿舰艏(x轴)无偏转。船体采用无滑移边界条件,计算域下表面选用零剪切应力壁面(与风洞实验条件相对应[15]),其余边界设置为压力远场。

3 数值方法验证

分别采用RANS和DES方法对SFS2全尺寸模型进行非定常计算。时间步长采用来流速度及船宽进行无量纲化:

Δt*=ΔtV0/b

(8)

式中，Δt为实际时间步长。参考文献[15,16,19]中采用的时间步长,选取Δt*=2.9×10-2,子迭代步数取10。计算基于定常模拟结果,在500个时间步之后对每个时间步的结果进行采样平均,共采样1 000个时间步,最终将得到时均结果与文献[15]中实验数据进行对比。

3.1 URANS数值模拟

采用k-ωSST湍流模型进行定常与非定常模拟。在飞行甲板长度50%、高度与机库平齐处取一条沿船宽的直线,读取该直线上的速度,并与实验数据进行对比。横坐标采用船宽进行无量纲化,纵坐标采用来流速度V0无量纲化,结果如图3所示。

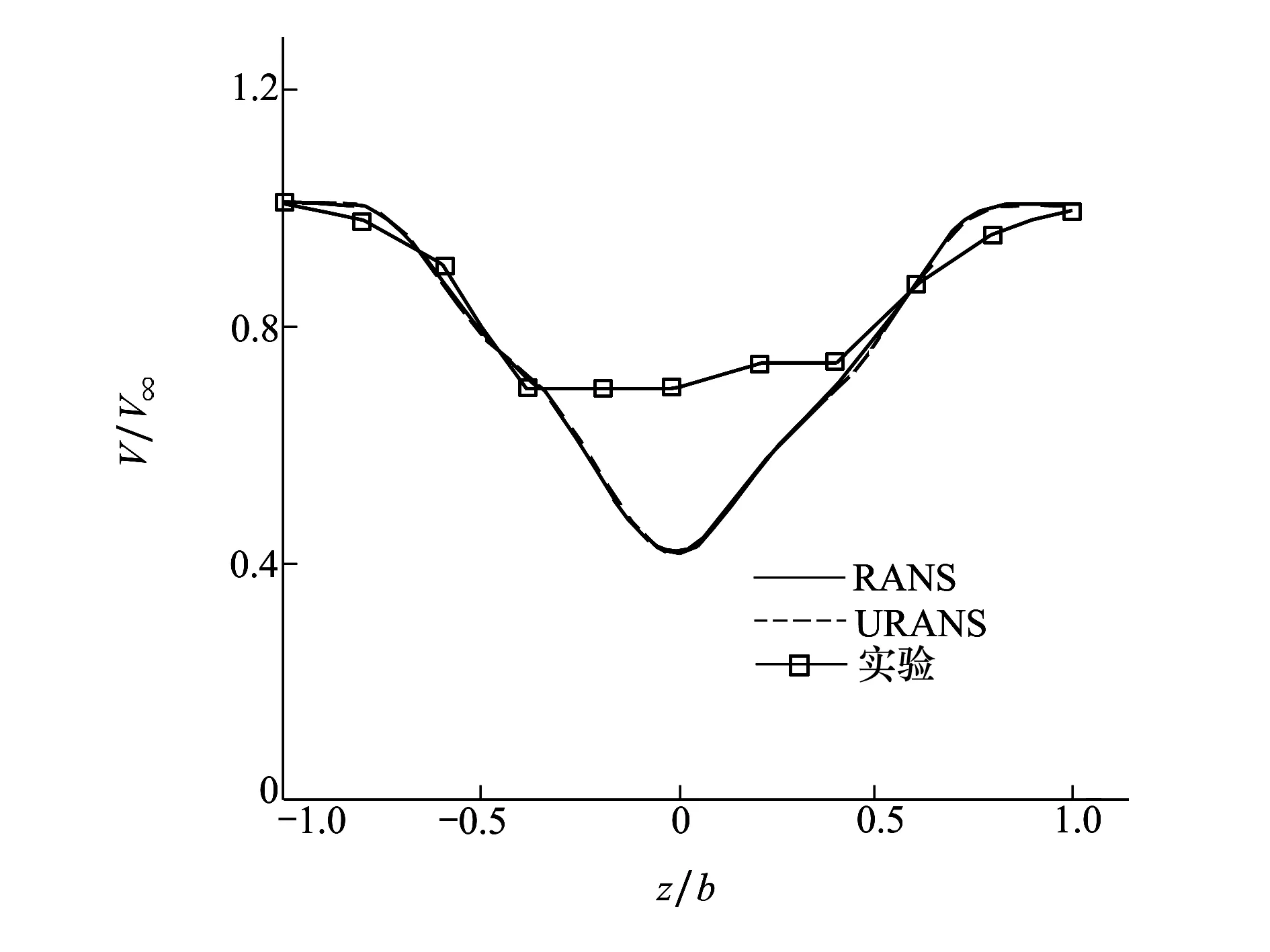
图3 不同方法Vx速度对比

k-ωSST湍流模型非定常计算所得时均速度分量Vx在船中轴附近同实验结果差距较大,而同定常计算结果基本一致。这是由于其计算并未捕捉到舰船流场的非定常流动特征,计算过程中阻力几乎没有波动,也说明了这一点。图4为定常计算z=0 m截面的速度云图,而非定常计算所得瞬态流场与其结果基本一致,这里便不再给出。因此,基于RANS的数值模拟对舰船空气流场的计算精度有待进一步提高。

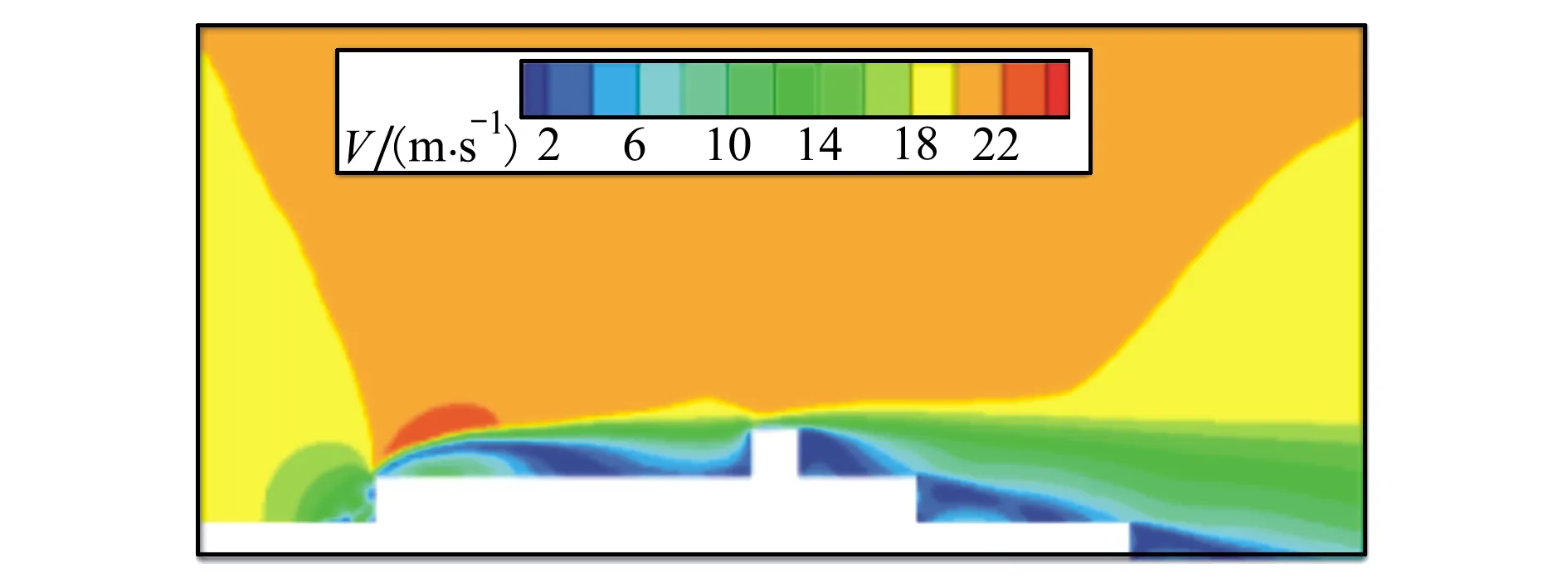
图4 RANS定常计算所得z=0 m截面速度云图

3.2 DES数值模拟

采用基于S-A和k-ωSST湍流模型的2种DES方法进行模拟。从图5展示的速度对比中可以看出,基于k-ωSST湍流模型的DES-SST方法得到的结果更加精确,其得到的瞬态速度云图显示出了舰船流场的非稳态特征,而时均结果与图4中RANS定常计算所得的流场结构基本相似,如图6所示。

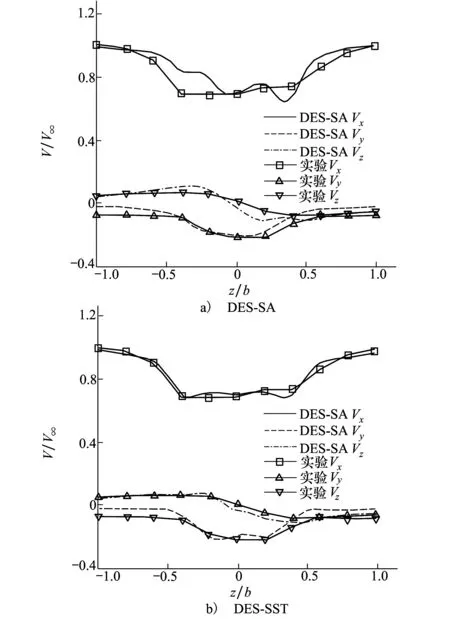
图5 2种DES计算结果速度分量对比

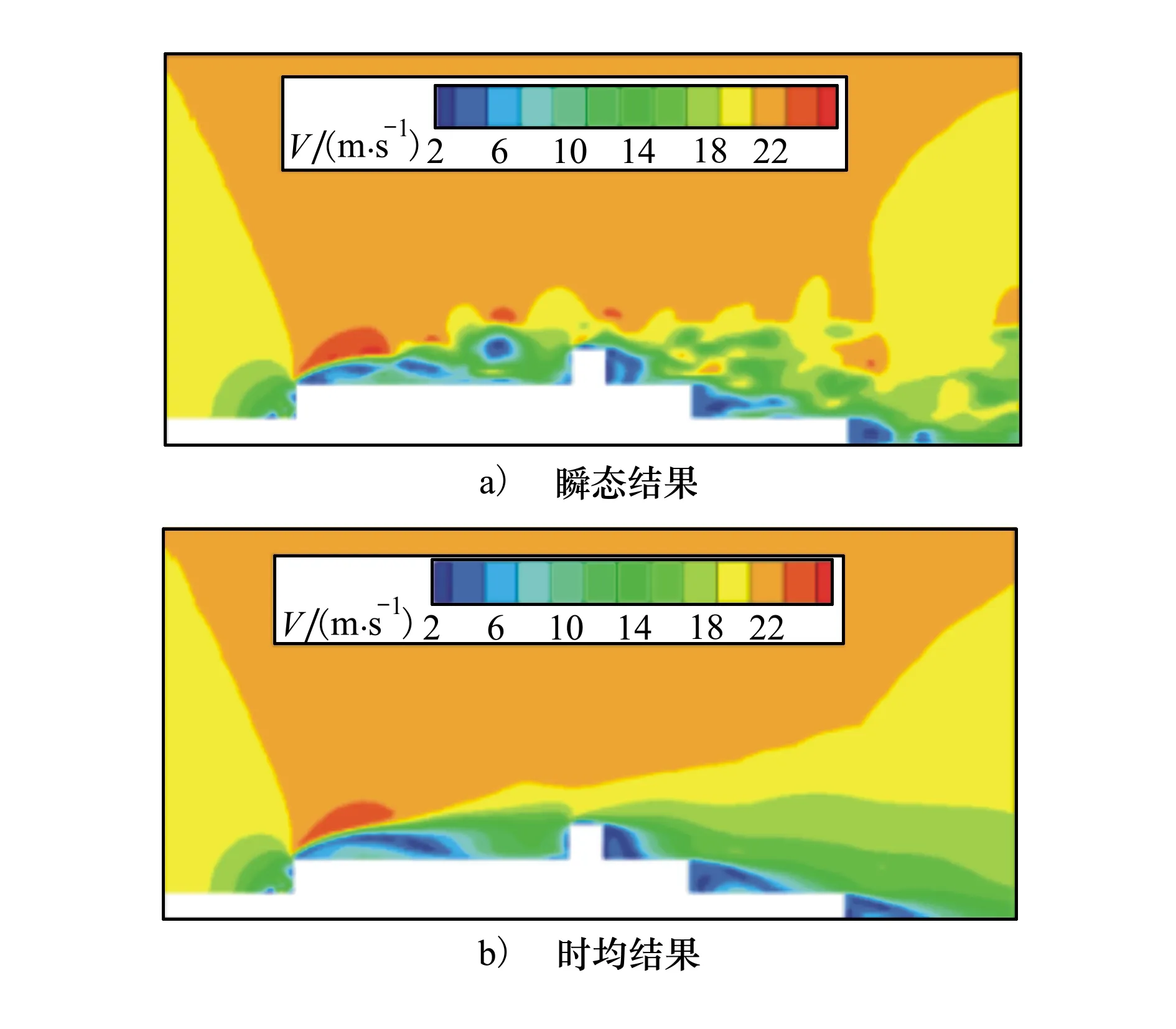
图6 z=0 m截面速度云图(DES-SST)

4 航母空气流场数值模拟

通过以上计算可知,由于RANS求解存在数值耗散,对旋涡主导的非定常流动具有阻尼抑制作用,不能捕捉到舰船流场的非稳态特征,而DES方法对这类高雷诺数大分离流动的处理有着较好的精度。因此采用DES方法对航母空气流场进行模拟。

4.1 几何模型与网格生成

计算选用简化航母模型,模型甲板长l0=260 m,宽b0=60 m,甲板高h0=17 m,采用斜角甲板,倾斜角为9°,舰载机的理想进舰轨迹正对斜角甲板中部,下滑角为4°。选择第2根和第3根阻拦索之间,距甲板3 m高的位置为理想着舰点,如图7所示。

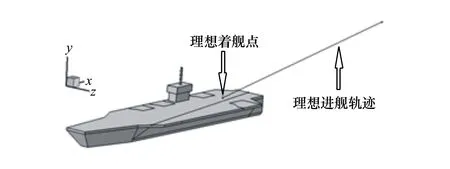
图7 航母简化模型及理想进舰轨迹示意图

采用结构化网格对整个计算域进行网格划分。参考SFS2算例验证,对航母周边及尾流区进行加密,选取网格尺度Δ0/b0=0.05,对舰岛后部甲板区域选取Δ0/b0=0.03。调整第一层网格距离保证y+≈1,生成网格单元总量为780万。

4.2 计算条件

为模拟航母在真实海面上的流场特征,考虑海面上风的影响,参考文献[21]对来流速度进行建模:

V=Vref(y/yref)α

(9)

式中，yref,Vref为参考高度及参考高度对应的速度,对于海平面常数α建议取为0.13[21],此外取Vref=21.8 m/s,yref=300 m,使甲板高度对应的风速为V=15 m/s。忽略航母的六自由度运动,对平行于海平面0°、左舷9°和右舷15°，这3个风向的空气流场进行模拟。计算采用DES-SST模型,取无量纲时间步长Δt*=2×10-2,其余计算条件同上。

4.3 三维流场结构分析

为分析流场的涡结构,采用Q准则[22]对涡核进行判断。Q值的定义为:

Q=1/2(‖Ω‖2-‖S‖2)

(10)

式中，Ω和S分别为速度梯度张量矩阵的反对称和对称部分,涡核存在于Q>0的区域。Q准则反映了流场中流体微元旋转和变形之间的平衡,定义了旋转占主导地位的涡核区域。

分析0°、左舷9°和右舷15°，这3个风向的甲板流场涡结构,如图8所示。从图中可以看出,航母流场中的涡流主要在甲板、舰岛等钝体的边缘产生,主要有:舰艏处的分离涡、舰岛处周期脱落的涡、尾部甲板后方由于陡壁效应形成的涡以及甲板两侧卷起的涡。

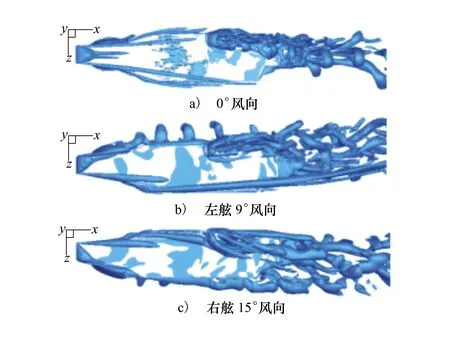
图8 不同风向航母流场涡结构

在舰艏舰载机起飞区域,涡流主要出现在甲板前端与两侧,其中处于前端的涡流对舰载机的起飞影响最大。而在航母后部舰载机降落区,由于舰岛的存在,产生周期性脱落的涡,并与右侧甲板卷起的涡相互作用,严重影响甲板右后方区域,之后其又与舰艉后方的涡流产生进一步耦合,在航母尾流区域形成复杂的涡系。其中,0°风向下涡流主要存在于右后方甲板及其后方的尾流区;右舷15°风向下,右侧甲板产生的涡向左翻起作用在舰岛与后方甲板,受其影响的甲板区域增加;而在左舷9°风向下,左侧甲板涡流的强度增大,而舰岛产生的涡向右偏离舰载机着舰区域。

4.4 进舰剖面流场分析

为了进一步明确舰载机进舰轨迹区域的流场特征,沿理想进舰轨迹垂直于xy平面截取进舰轨迹剖面,并通过Q值云图显示不同风向下该剖面的瞬态涡结构,如图9所示。图中直线为理想进舰轨迹,着舰点位于x=210 m处。

可以看出,0°风向下甲板后部及尾流中的进舰运动轨迹区域存在多处涡流,这将对舰载机着舰产生不利的影响;同样在右舷15°风向下,涡流向左偏移,在舰载机降落区域产生的影响也随之变大;而在左舷9°风向下,进舰轨迹区域的涡流相对较少,而左侧甲板卷起的涡尚未影响到降落区域,此时有利于舰载机的安全降落。

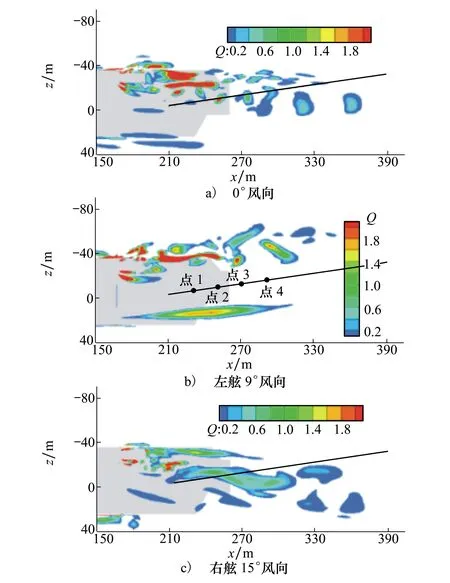
图9 理想进舰轨迹剖面瞬态Q值云图

4.5 进舰轨迹速度分布对比

图10展示了不同风向进舰轨迹上的速度分布时均值,从图中可以看出,左舷9°风向下速度分布的波动最小,这也进一步说明了该风向对舰载机的降落有利;而在右舷15°风向下,速度波动的幅值最大,其中在接近航母尾部时,3个速度分量均产生较大的变化,此时由于进舰轨迹末端处于舰岛产生涡流之中,Vy由上洗变为下洗,对舰载机的安全降落提出挑战。

4.6 0°风向进舰轨迹速度波动

以0°风向角计算状态为例,图11展示了t=48 s,t=49.2 s及t=50.4 s 3种瞬态下理想进舰轨迹上的速度分布,并将其同时均结果相比较。结果表明,速度波动主要存在于着舰前的200 m,即x=210～410 m范围内;而瞬态与时均速度分布的差异主要存在于后部甲板及其临近的尾流区,尤其是在侧向和垂向,大强度的侧风与上下洗将严重影响舰载机的降落,这是定常计算所不能得到的。

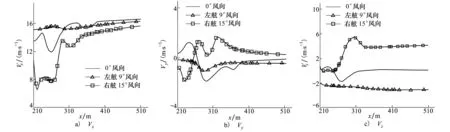
图10 理想进舰轨迹上的时均速度分布对比

图11 理想进舰轨迹上不同时刻瞬态速度分布对比

从图11中可以看出,相比于时均结果,瞬态速度的波动主要存在于临近船尾的范围内,在该范围进舰轨迹上选取4个点,如图9b)所示,于数据采样平均过程监视其速度变化情况,得到速度波动范围如表1所示。

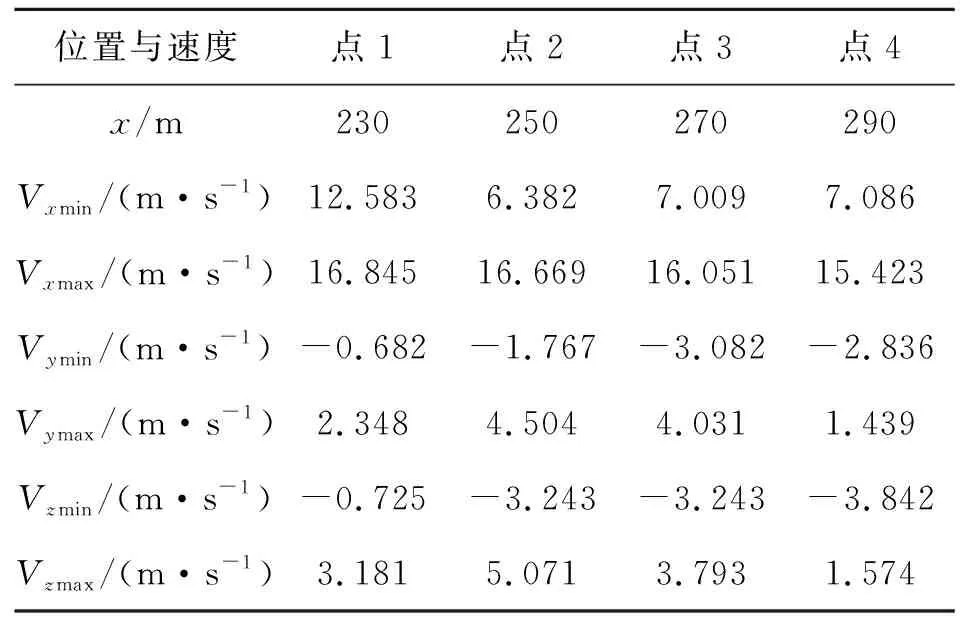
表1 监视点速度波动范围

表1表明进舰轨迹上各点速度的大小及方向随着时间推进而变化。点2、3接近甲板末端,3个方向速度的波动幅值较其他两点大。而随着远离甲板末端,进舰轨迹上各点速度波动逐渐放缓。

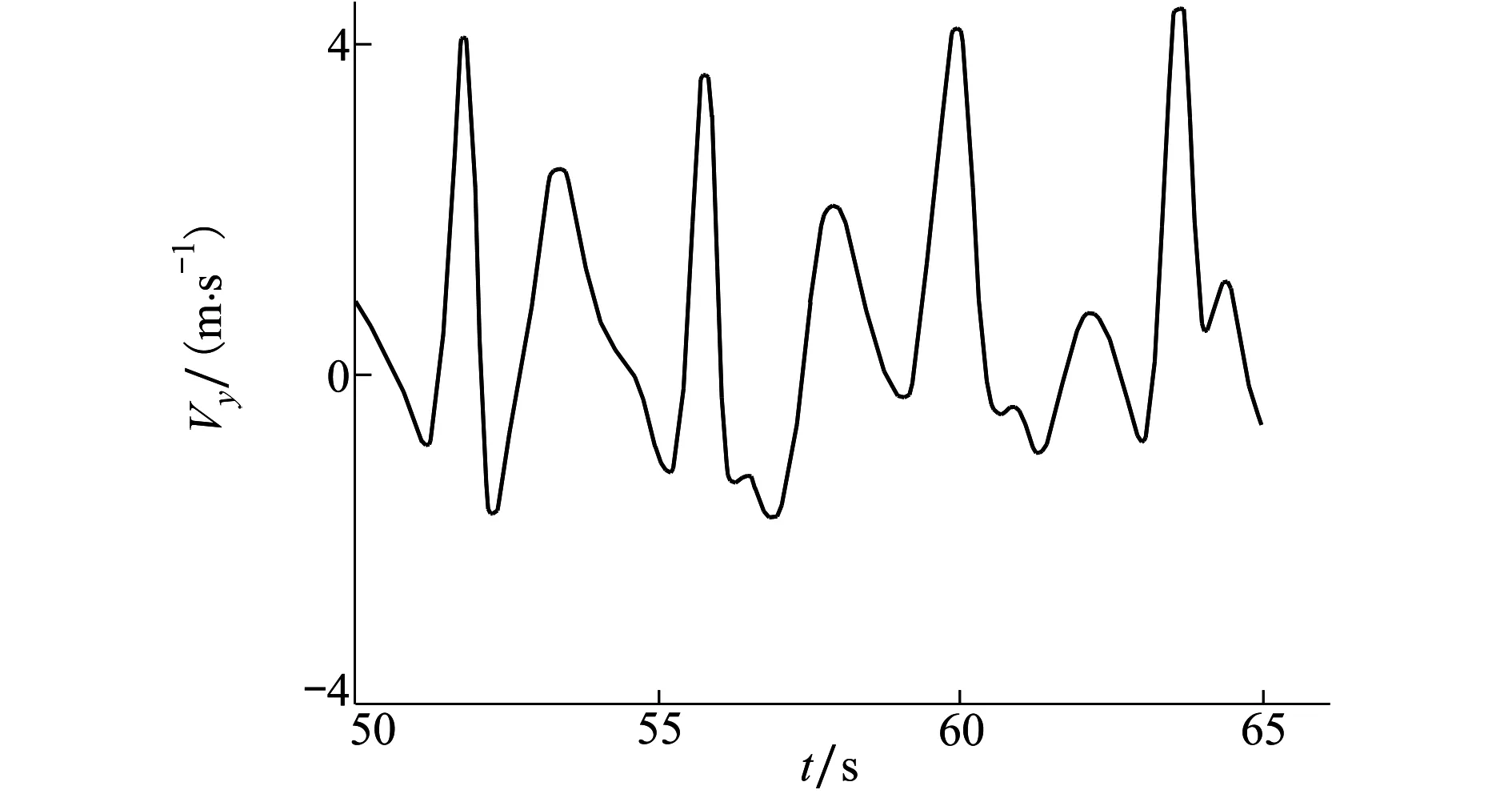
图12 点2处Vy速度随时间的波动

观察t=50～65 s时间段内点2处Vy速度随时间的变化,如图12所示。该状态下速度波动的周期为4 s左右,且存在短时间内上下洗的变化,这将影响舰载机的安全降落。

5 结 论

本文对比了不同数值方法对舰船空气流场的模拟结果,对舰船空气流场数值模拟方法及流场特征进行了探索,得出的结论如下:

1) 舰船空气流场体现出非稳态特征,基于RANS的非定常计算并不能够模拟出该特征,但基于RANS定常计算得到的流场结构与DES方法取得的时均结果相似。而基于DES的数值模拟能够较好地捕捉舰船空气流场中涡的生成和发展,其中基于k-ωSST湍流模型的DES-SST方法所得结果更为准确;

2) 航母流场中最为突出的是舰岛处周期性脱落的涡,及其与甲板边缘、尾部涡流相互作用形成的复杂涡系。这些涡流在舰载机进舰轨迹上引起较为强烈的且随着时间推进的速度波动,导致在航母后部甲板及其临近的尾流区产生大的侧风及上下洗变化,其中甲板末端表现最为显著;

3) 不同风向下,航母甲板受涡流影响的区域范围不同,其中左舷9°风向下舰载机进舰轨迹区域的涡流相对较少,且进舰轨迹上的时均速度波动较为平缓,对舰载机着舰有利。