高动态环境下联合开环捕获和闭环跟踪的载波同步算法

韩春雷, 白滢钰, 司江勃

(1.中国电子科技集团公司 第二十研究所, 陕西 西安 710068; 2.西安邮电大学, 陕西 西安 710100;3.西安电子科技大学, 陕西 西安 710071)

在高动态环境中，通信双方之间的高速相对运动往往会在接收机接收信号上引入较大的多普勒频率及其高阶变化率。为了适应高动态环境，捕获和跟踪接收信号中的多普勒频率及其变化率，就必须加宽中低动态接收机载波跟踪环路的环路带宽。然而环路带宽的加大势必降低载波跟踪精度，当跟踪环路处于低信噪比通信环境中时尤为如此。噪声的引入甚至会导致载波跟踪环失锁。因此，在动态适应力和跟踪精度之间的权衡，一直吸引着许多学者进行深入的研究。 高动态环境下常用的跟踪技术包括基于Kalman滤波器的跟踪技术、基于最大似然的跟踪环技术以及基于锁频环(FLL)辅助的锁相环(PLL)技术等等。其中，基于Kalman滤波器的跟踪方法通过自适应地调整环路参数对载波相位差、多普勒频率及其变化率进行估计。然而，由于高动态环境对系统稳定性的影响较大，该方法无法实现快速捕获[1-2]。基于最大似然辅助的环路跟踪算法是一种渐进无偏估计，其参数的估计方差接近于Cramer-Rao下界(CRLB)，但由于进行二维或三维搜索所需的存储量和计算量很大，导致算法跟踪速度变慢[3-4]。在FLL辅助PLL的结构中，FLL和PLL分别用作载波参数的同步和细同步，并由PLL决定最终的跟踪精度。这种方法的结构相对简单，但由于FLL环路带宽较大，引入附加的噪声功率，降低了跟踪精度[5]。为了解决这些问题，本文提出了一种联合开环捕获和闭环跟踪的高动态载波同步算法。即通过开环阶段能够实现快速捕获，同时通过PLL实现高精度载波跟踪。该算法不仅具有较高动态适应能力，也具有较大的多普勒频率及其变化率的估计范围。本文的贡献有以下2点：①适用于高动态通信环境的线性频率变化情况；②估计范围大，精度高。

1 系统模型

接收机的结构框图如图1所示。该接收系统的包括开环捕获和闭环跟踪2个部分。其中开环部分采用前导序列粗略估算出多普勒频率和多普勒变化率，闭环部分采用三阶PLL跟踪剩余多普勒频率和多普勒变化率并解调得到译码信息。

图1 接收机载波同步系统框图

2 开环捕获

在捕获操作中，利用了最小均方误差(MMSE)方法获得多普勒频率偏移及其变化率偏移粗估计值。假设接收到的复基带信号可以表示为：

r(t)=s(t)·ej(θ+Δft+0.5Δat2)+n(t)

(1)

式中，s(t)是已调信号,θ是载波的初始相位,Δf是多普勒频率偏移,Δa是多普勒变化率偏移,n(t)表示高斯白噪声,导频长度为N,符号周期为T。Δf和Δa相应的对数似然函数为[6]

(2)

基带信号相位为[7]

(3)

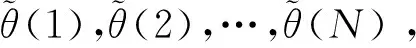
(4)

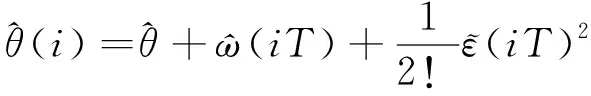
(5)

(6)

(-iT)

(7)

(8)

结合(6)～(8)式可以得到最终结果:

式中,计算系数αN,βN,γN分别表示如下

由于(9)式和(10)式推导出的多普勒频率偏移和多普勒变化率偏移估计公式是闭式解形式,因此其复杂性是相当低的,能够实现快速捕获,适应高动态环境,快速得出多普勒频率偏移和多普勒变化率偏移粗估计值。

3 闭环跟踪

虽然经过开环捕获后,剩余多普勒频率偏移与变化率偏移已经控制在一个很小的范围之内,但相位误差仍会随着时间推移而增加。由于三阶环拥有跟踪加速度的能力[8],因此可以用来跟踪多普勒变化率。本文的闭环跟踪三阶环路滤波器的结构如图2所示[9]。

图2 三阶环路滤波器

其中,Z-1表示延时器,NCO表示数控振荡器,C1,C2,C3表示滤波器参数,其值如下所示

(14)

(15)

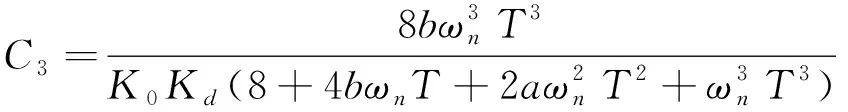
(16)

式中，Kd为鉴相器增益,K0为NCO增益,a=1.1,b=2.4为阻尼系数等于0.707的经验值,ωn为环路固有频率,与环路的等效噪声带宽的关系为

(17)

4 仿真分析

基于图1所示的系统模型对本文提出的联合开环捕获闭环跟踪算法进行仿真验证。系统的各个仿真参数如下:采用QPSK调制,每帧1 000 bit数据,128 bit导频,信噪比范围设为(6 dB,12 dB),归一化多普勒频率偏移和多普勒变化率偏移范围分别为(-0.25,0.25)和(-10-4,10-4)。为验证本文提出的载波同步算法,分别对相位跟踪曲线和误码率进行数值仿真。

在图3中,当环路带宽Bp=0.02时,约在700个数据符号之后该系统能稳定跟踪参数。而当Bp=0.04时,达到稳定跟踪需要约420个数据符号长度。当Bp=0.06时,该系统跟踪载波信号仅需要300个数据符号。由该三阶锁相环的相位跟踪曲线图可以看出,三阶锁相环的环路带宽Bp越高,系统进入跟踪阶段的速度越快。

图4给出了,在归一化多普勒变化率偏移ΔaT2=0.000 1,不同的环路带宽Bp,以及不同的多普勒频率偏移条件下,系统的误码率随着信噪比变化的曲线,其中理论值为不存在多普勒频率偏移和多普率变化率偏移的理想情况。从图4a)可以看出,当Es/N0≥8 dB,Bp=0.04和Bp=0.02时,误码率曲线和理论值非常接近;同时环路带宽越高,误码率越高。结合考虑图2中的跟踪时间和图3中的误码率,我们认为选择环路带宽Bp=0.04更适合于进一步分析。由图4b)可知,当Es/N0=8 dB,归一化多普勒频率偏移ΔfT=0.2时,误码率相比理论值仅损失1.1 dB。当归一化多普勒频率偏移ΔfT=0.15时,误码率相比理论值仅损失0.7 dB。

图3 相位跟踪曲线 图4 误码率曲线

5 结 论

本文提出了在高动态环境下联合开环捕获和闭环跟踪的载波同步算法。该算法将两者结合并发挥两者各自的优势,从而可以实现快速捕获和精确跟踪。当信噪比为8 dB,归一化多普勒频率偏移ΔfT=0.15和归一化多普勒变化率偏移ΔaT2=10-4时,误码率相比理论值仅损失0.7 dB。