一种可变流量系数的通气短舱匹配方法

2019-01-18闫海津杜玺

航空学报 2018年12期

闫海津，杜玺

中国商飞北京民用飞机技术研究中心民用飞机设计数字仿真技术北京市重点实验室，北京 102211

为了降低飞机的使用成本，满足绿色航空的要求，耗油率较低的大涵道比发动机得到普遍应用，更大的涵道比意味着更大的发动机短舱尺寸，因此对于发动机短舱本身以及短舱对机翼机身影响的研究越发重要，飞机发动机一体化设计成为了大家关注的焦点[1]。发动机的内部工作过程是相当复杂的[2-3]，在飞机气动设计及飞机发动机一体化研究中通常更加关注短舱外罩和进气道的气动特性以及短舱对飞机的影响[4-6]，通常在机翼气动设计以及全机测力测压风洞试验中，使用通气短舱(Through-Flow Nacelle, TFN)代替动力短舱(Powered Nacelle, PN)模拟短舱和进气道效应，以简化设计流程和降低试验成本[7-9]，对于飞机气动化设计和风洞试验都有重要意义。

传统的通气短舱匹配方案是保留短舱外罩和进气道外形不变，简化动力短舱的进排气系统，在短舱内部增加一个通气内涵，或者将风扇涵道形面沿其倾角延伸或截短，再用等直段取代原来的喷管曲面，前缘过渡保证曲率连续[9]。两种方法都是通过改变内涵的出口面积控制通气短舱的流量系数(Mass Flow Ratio, MFR)，该方法在改变流量系数的情况下需要重新匹配通气内涵。

在民机巡航状态下，随着飞机燃油消耗，飞机总重降低，包含几个不同飞行高度，飞机实时配平所需的推力会发生变化，进气道进口流量随之变化。为了在风洞试验和气动计算时实现连续、快速地改变流量，在独立短舱风洞试验中分析流量系数变化对短舱进气道和外表面流动的影响，本文采用锥形堵块的方式替代通气内涵，通过改变堵锥位置可以快速获得不同流量系数的通气短舱。该方法目前在民机气动设计与试验验证过程中还未发现先例。与传统通气内涵方法相比较，本文的方法在结构上更加简单，风洞试验中可连续地改变流量系数，气动计算中的网格拓扑更加简洁，在设计、计算和试验等各环节中都可节约成本。

1 通气短舱流量匹配原理

通气短舱流量匹配主要是控制通气短舱的流量，使其流量系数与所对应的动力短舱特定状态下的流量系数一致，只要保证了流量系数一致，那么就可以获得与动力短舱外罩和进气道基本相同的压力分布与激波形态。传统通气短舱的匹配方案是保留短舱外罩和进气道外形不变，简化动力短舱的进排气系统，在短舱内部增加一个通气内涵，如图1所示。

流量系数是指进入进气道的实际空气质量流量与同一马赫数下能够进入进气道的理论最大质量流量之比，即

(1)

式中：ρ∞为远场空气密度，其数值根据飞行高度得出，kg/m3；V∞为远场来流速度，其数值根据马赫数与当地声速的乘积得出，m/s；A∞为进气道的自由流管面积，反映了实际进入进气道的空气流量，m2；AHL为进气道的进口面积，反映了能够进入进气道的最大流量，m2。

对于通气短舱而言，进气道的进口面积即唇口面积已经确定，远场条件已知，那么根据流量系数的定义可以计算得出能够进入进气道的最大流量。通气短舱与自由流管形成流道，自由流管面积难以捕获。根据连续性方程，自由流管内的流量不会发生变化。其空气流量可在通气短舱内截取某一通流截面进行积分得到。通气短舱的流量系数可转化为通气短舱内任一截面积分得到的流量与计算得出能够进入进气道的最大流量的比值。

本文工况下，通气短舱堵锥形成的流动为亚声速气流，其流量与流道的最小面积密切相关。因此只需通过改变堵锥与短舱出口的轴向相对位置，利用堵锥调节实际出口面积即可实现流量系数的调节[9]。想要快速获得不同流量系数的通气短舱只需保证短舱出口面积能够连续变化。基于以上分析，本文提出了以堵锥的方式匹配流量系数，如图2所示，通过前后移动堵锥可便捷、连续地在试验和计算中获得不同流量系数的通气短舱方案。

图1 传统通气短舱匹配方案Fig.1 Traditional matching method for TFN

图2 通气短舱堵锥匹配方案Fig.2 Conical plug matching method for TFN

2 通气短舱堵锥设计

通气短舱堵锥的设计原则是表面无激波，流场无分离，在能够保证出口面积连续变化的情况下尽量靠近短舱出口处。堵锥的设计参数包括：堵锥半径、等直段长度、尾部长度、尾部收缩角、头部长度等。堵锥面的轮廓曲线采用SPLINE样条曲线，堵锥半径决定了最小流量系数，因此半径值可根据流量系数所需变化范围给定，等直段长度可尽量减小，尾部长度以不产生流动分离为标准，尾部收缩角度参考动力短舱尾锥角度，一般不超过20°，各条曲线过渡段保证曲率连续，可以使得流动平稳，避免激波出现和发生分离。图3给出了本文使用的堵锥轮廓线。堵锥型面由轮廓线绕流向轴线旋转而成。

图3 堵锥轮廓线示意图Fig.3 Contour of conical plug

3 边界条件及网格

为了证明通气短舱在流量系数与动力短舱一致的情况下能够反映短舱的气动特性，本文针对动力短舱在巡航工况下进行了数值模拟分析，并与相同流量系数下的通气短舱的结果进行了对比分析。图4和图5分别给出了动力短舱模型示意图和通气短舱在两个不同流量系数状态下的示意图。

图4 动力短舱模型示意图Fig.4 Schematic diagram of PN model

图5 通气短舱不同状态示意图Fig.5 Schematic diagram of TFN in different statuses

3.1 边界条件

本文数值模拟的通气短舱由于不涉及发动机进排气系统，因此除远场设置自由流动和对称边界条件外，短舱和堵锥表面均设置为无滑移壁面边界条件。远场来流工况根据巡航状态环境条件给出，具体参数设置如表1所示。

本文数值模拟的动力短舱巡航状态进排气的边界条件根据发动机的实际流量得出。风扇入口(图6中红色部分)作为流场出口条件给定压比。风扇出口、核心机出口(图6中绿色部分)作为流场入口条件分别给定总压比、总温比和攻角，其余短舱表面与通气短舱相同，均设置无滑移壁面边界条件[10-12]。进排气边界条件的具体参数见表2。

表1 巡航工况来流条件Table 1 Flow condition of cruise status

图6 边界条件设置示意图Fig.6 Schematic diagram of boundary condition settings

表2 动力短舱巡航工况边界条件Table 2 Boundary conditions of powered nacelle in cruise status

边界静压比总压比总温比风扇入口1.24风扇出口2.451.38核心机出口1.943.16排气出口1.202.68

3.2 网格

本文利用ICEM软件对动力短舱和通气短舱的半模三维流场生成了结构化网格，通气短舱包括最大流量状态、中间流量状态和最小流量状态3套网格。远场边界前后距离为短舱长度的50倍左右，周向距离为短舱最大直径的50倍左右。为了准确地模拟附面层内的复杂流动，对短舱近壁面处进行了加密处理，第1层网格高度约为0.001 mm，网格增长率为1.15。另外对进气道唇口处、堵锥周围、动力短舱进排气系统以及短舱外罩周围等流场参数变化较为剧烈的区域网格进行了适当的加密处理[13-15]，通气短舱网格数量为320万左右，动力短舱网格数量为960万左右[16-17]，其中通气短舱3种状态下的网格拓扑结构相同。图7和图8给出了动力短舱和通气短舱在巡航流量系数状态下的表面网格及其对称面切面网格的示意图。

图7 动力短舱网格示意图Fig.7 Schematic diagram of PN mesh

图8 通气短舱网格示意图Fig.8 Schematic diagram of TFN mesh

4 计算结果与分析

本文以数值模拟的方法对动力短舱和通气短舱进行分析研究。采用的内部结构化网格CFD程序为基于三维雷诺平均Navier-Stokes方程的求解器，该程序采用有限体积方法，空间离散采用二阶精度，通量计算采用Roe格式，时间推进为LU-SGS(Lower-Upper Symmetric Gauss-Seidel)隐式方法。该程序已经通过了大量算例的计算验证，其计算精度能够满足工程需求[18]。本文数值模拟选取Menter’sk-ωSST(Shear Stress Transport)湍流模型[19-22]，并采用了多重网格技术和并行计算技术以加速收敛。

4.1 同流量系数下通气短舱与动力短舱的结果

图9给出了动力短舱与通气短舱相同流量系数状态下在0°、90°和180°这3个不同站位短舱外罩和进气道压力系数(Cp)分布对比情况，横坐标(x)为短舱的弦向坐标归一化值，可以看出通气短舱和动力短舱的压力系数分布在不同站位都吻合良好，激波位置和强度基本重合，由于短舱尾缘存在一定厚度，导致了压力系数在最右侧突然上升。

图9 相同流量系数下动力短舱与通气短舱压力系数分布对比Fig.9 Comparison of pressure coefficient distributions of PN and TFN at same MFR

4.2 通气短舱不同堵锥位置的结果

在以上研究的基础上，针对通气短舱堵锥的不同位置开展数值模拟工作，来流条件为马赫数为0.85、攻角为4°，分别模拟了最大流量系数状态、中间流量系数状态和最小流量系数状态这3种典型状态。图10给出了3种典型状态通气短舱对称面上的马赫数云图和流线图，可以看出在3种状态下通气短舱的流线形态过渡平稳，流场结构合理，堵锥表面没有出现激波和流动分离的情况。随着堵锥的向后移动，通气短舱的出口面积逐渐减小，所以流量系数逐渐减小，流经喉道的气流速度减小，喉道附近的超声速区域消失。短舱外罩的激波形态变化不明显。

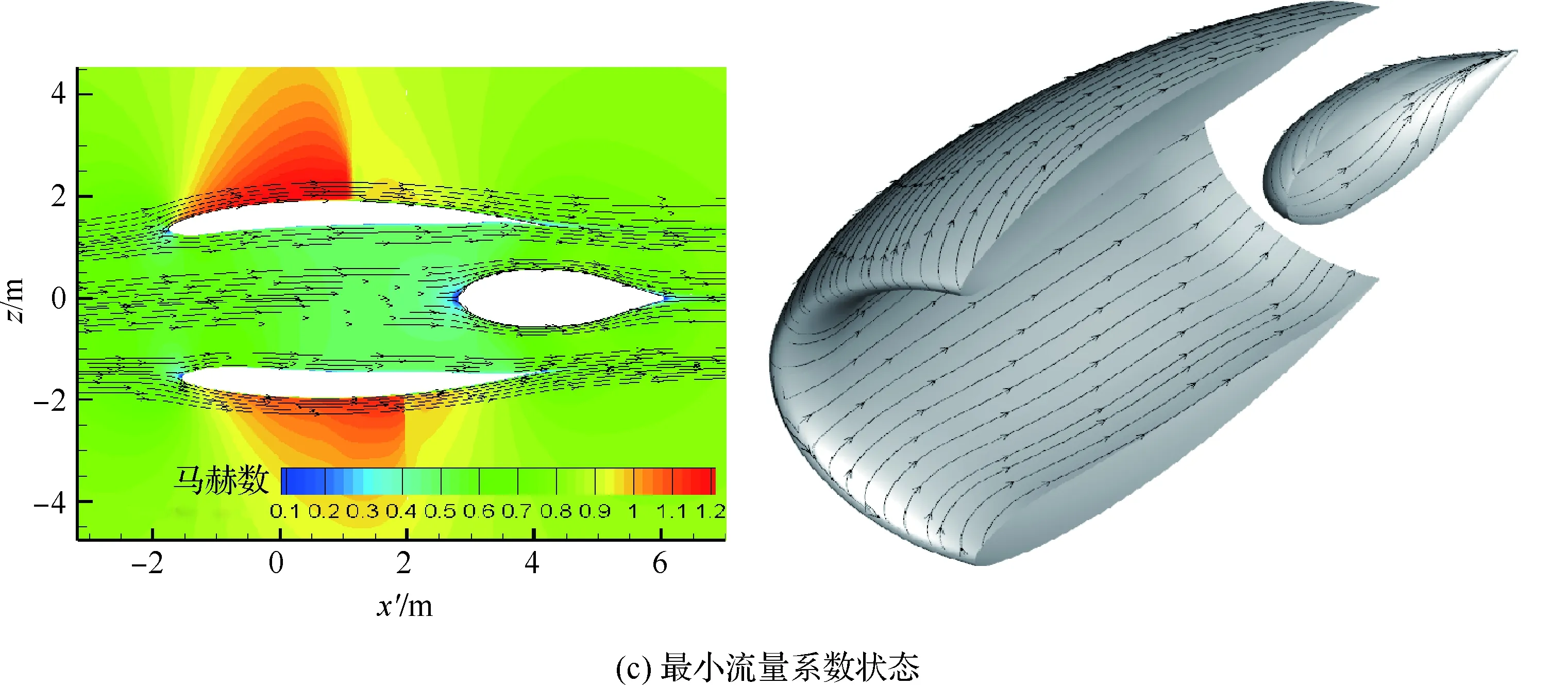
图10 3种典型状态通气短舱对称面马赫数云图和流线Fig.10 Mach contours and streamlines at symmetrical plane of TFN under three typical statuses

图11给出了3种典型状态下通气短舱0°站位的短舱外罩和进气道压力系数分布情况，通过该图可以更加直观地反映出在不同流量系数下短舱和进气道气动特性。可见随着流量系数减小，进气道内的流速明显减小，同样随着进气量的减少，短舱外罩靠近唇口处的流速有所增加，但总体而言流量系数的变化对短舱外罩的激波位置和激波强度影响不大。

图11 3种典型状态下通气短舱0° 站位压力系数分布Fig.11 Pressure coefficient distributions of TFN with three typical statuses at 0° position

4.3 流量系数与通气短舱出口面积的关系

通过对比分析通气短舱不同堵锥位置下的流量系数可以看出，流量系数与通气短舱出口面积呈正比关系。图12给出了不同堵锥位置下对应的通气短舱出口面积(S)与流量系数(φ)的关系，可见流量系数与短舱出口面积基本呈线性关系，但在后期的工作中发现，当通气短舱内部出现激波时该结论不再适用，原因是激波对流动造成的影响改变了通气短舱流量。根据该结论，在以后的通气短舱匹配工作中如果短舱内无激波出现，那么只需计算两个不同出口面积下的流量系数，然后就可以利用这种线性关系进行插值得出任意出口面积对应的流量系数。

图12 通气短舱出口面积与流量系数关系Fig.12 Variation of MFR with exhaust area of TFN

4.4 通气短舱方案鲁棒性分析

为了验证该方法得出通气短舱方案的鲁棒性，本文在马赫数为0.85、攻角α为0°～6°变化范围内和攻角为4°、马赫数为0.83～0.87变化范围内对通气短舱进行了数值模拟，分析了攻角变化以及马赫数变化对通气短舱流量系数的影响。

如图13所示，在马赫数为0.85、攻角为0°～6°的范围内，流量系数变化只有0.15%，可见，在巡航状态附近攻角变化对该通气短舱流量系数几乎没有影响。

如图14所示，在攻角为4°、马赫数Ma为0.83～0.87的范围内，流量系数变化只有0.56%，可见，在巡航状态附近马赫数变化对该通气短舱流量系数的影响也很小。

图13 流量系数随攻角的变化Fig.13 Variation of MFR with angle of attack

图14 流量系数随马赫数的变化Fig.14 Variation of MFR with Mach number

5 设计方法验证

该设计方法已经应用在单独通气短舱风洞试验中，该试验目的旨在验证设计的短舱在巡航状态下的气动性能，主要测量短舱表面压力分布，研究马赫数、雷诺数、攻角、流量系数对短舱气动特性的影响。马赫数、雷诺数和攻角等参数的变化可由风洞实现，流量系数的变化由本文的设计思路完成的方案实现。具体方案如图15所示。

试验模型由一个类似吊挂的装置连接到风洞的支撑设备上。图15中灰色部分为固定结构，堵锥由3个叶片支撑，堵锥的红色部分通过安装在堵锥内的遥控步进电机控制前后移动，实现流量系数的连续变化，所有测试点一次性全部完成，缩短了约75%的试验时间，大大节约了试验成本。

在马赫数为0.85、攻角为4°、雷诺数为3×107、温度为138 K、总压为290 kPa的风洞试验条件下，针对试验构型同样进行了详细的CFD分析，其过程与前文相似，这里不再赘述，图16反映了不同堵锥位置下试验和CFD计算流量系数的对比情况，横坐标(l)为堵锥伸缩长度归一化值，纵坐标为试验测试和计算所得流量系数。可见试验测得流量系数与相同构型下CFD计算值吻合良好，验证了本文设计方法的可行性。