纯电动船复合储能系统的设计与优化*

徐宏东，高海波，林治国，杜康立，卢炳岐，杨再明

（武汉理工大学 能源与动力工程学院，武汉 430063）

0 引 言

随着储能技术的进步，由储能装置作为动力源的纯电动船舶发展迅速，目前纯电动船舶上的储能系统大多采用动力电池。航行时电网的功率需求会频繁产生波动，动力电池组受到瞬态大电流的冲击，会加快其容量衰减的速度。对此，学者们提出了复合储能装置的构想以达到提高船舶动力系统性能、延长电池使用寿命的目的。

国内外对复合储能装置的应用进行了大量研究。TROVÃO等[1]采用被动式复合电源结构，对复合电源中的超级电容与电池的容量配比进行研究，但未能充分发挥超级电容的作用。SHIN等[2]利用空间搜索算法，对电池和超级电容的容量进行了协同优化，提高了系统的能量密度。宋子由[3]利用动态规划算法，对复合储能机构进行参数和能量管理策略的联合优化，提高了优化的有效性。但针对纯电动船舶具体工况进行复合储能的系统设计与优化还鲜有报道。

本文以100客座的纯电动客船为研究对象，开展储能系统配置方案的论证，进行复合储能装置中电池和超级电容的选型配比方法以及系统优化设计的相关研究，并设计仿真实验进行验证。

1 纯电动船复合储能理论论证

在优先满足安全性能的前提下，可以采用锂离子蓄电池及超级电容器组成的复合电池作为纯电动船舶的储能装置[4]。复合储能装置的连接方式主要有直接并联、通过DC/DC变换器并联、通过电感并联等。由于并联电感的方式与直接并联结构类似，且输出电压波动较大，因此本文只研究直接并联式和通过DC/DC变换器并联两种连接方式。

1.1 直接并联混合储能的理论计算

1.1.1 磷酸铁锂电池选择及容量计算论证

以100客位的 Arsterwasser号的功率需求为参考进行计算，该船舶1 h的功率需求如图1所示[5]。

图1 母型船功率需求曲线[5]Fig.1 Parent ship power demand curve

从图1中可以看出，船舶工作时的功率呈现周期性变化且有时周期较短，为了便于后续计算和能量管理策略的仿真分析，从图中截取350 s典型功率需求，包含定速航行、加减速及停船工况，如图 2所示[6]。图中功率需求曲线可大致分为定速航行工况和机动航行工况，其中0 ～ 85 s和200 ～ 350 s为定速航行工况，功率需求为42 kW，由电池模块承担。纯电动船舶每天工作8 h，大部分功率需求由电池承担，所需电池容量Q1为42 kW × 8 h = 336 kW·h。考虑到安全余量，电池的总容量设计为400 kW·h，安全裕度为 13.4%。机动航行工况的功率需求波动较大，大部分应由超级电容所承担，对功率图谱中机动航行工况的功率需求进行积分计算，每个典型工况周期中超级电容所应提供的能量为1 kW·h。

参考船舶直流母线电压为580 V，计算出电池所需要的总容量为PAh= 689.4 A·h，满足电池容量要求，按照700 A·h容量来配置电池，采用中航锂电公司的CA100型动力电池。磷酸铁锂单体的标称电压为3.2 V，需要串联的单体个数为N：

182个电池串联成一组，可提供的电池平均电压为582.4 V，可以满足直流母线的供电需求。电池的单组容量为100 A·h，故需要并联的电池组为7组。

图2 典型工况功率需求曲线[6]Fig.2 Power demand curve of typical working condition

1.1.2 超级电容选择及容量计算论证

综合考虑等效串联电阻、漏电流、电容器体积等因素，选用表1所列超级电容器进行设计计算。

表1 超级电容系列规格Table 1 Super-capacitor series specifications

根据电容最大放电量Ec为1 kW·h可计算出各型号理论个数n=EcWc，Wc为单个电容的放电量，每组串联数n=UUc，并联组数m=Ec（Wc⋅n） ，实际电容元件总数n×m。各备选型号电容的配置方式见表2。

表2 各型号超级电容理论配置方式Table 2 The theoretical configuration of various super-capacitor

1.2 联合供电特性分析论证

本研究的设计思想是稳定负载由磷酸铁锂电池组承担，瞬态负载主要由超级电容所承担。

对应表2中6种超级电容，可以有6种不同的配置方案。整个混合供电系统可提供的瞬时功率可表达为：

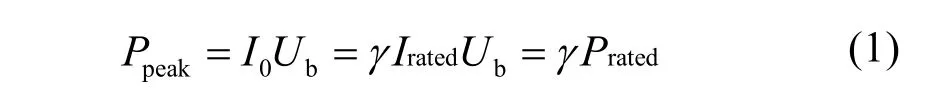
其中，Prated为磷酸铁锂电池可提供的额定功率，Irated为磷酸铁锂电池提供的额定电流，Ub为磷酸铁锂电池的等效电压，I0为负载的电流幅值，γ为功率增强因子，衡量应对脉冲性负载时超级电容的响应情况[7]。采用联合供电模式，铁锂电池和超级电容全部投入。依照文献[2]，混合动力系统的固有频率为：

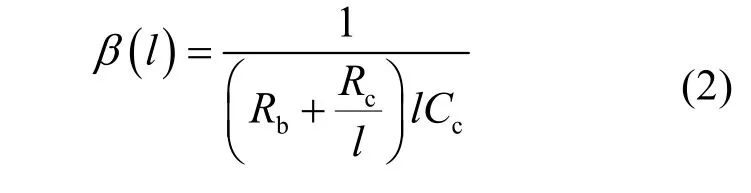
其中，Rb是整个电池组的等效内阻，Rc是单个电容模块的内阻，Cc是单个电容的电容值，l为电容并联支路数量与串联单体数量的比值。

根据文献[2]，功率增强因子可以表示为：

其中，D为脉冲负载的占空比；T为脉冲负载的周期，若定义f为脉冲负载的频率，则T= 1/f。

分别计算每种型号的超级电容与铁锂电池组直接并联的功率增强因子，计算结果如表3所示。可知在电池组上直接并联不同型号超级电容的6种方案来应对脉冲性负载时，瞬态功率改善情况均不明显，主要是超级电容串联组数太多，导致等效内阻远远大于铁锂电池组的等效内阻所致。

表3 不同配置方案下的功率增强因子Table 3 Power enhancement factors for different configuration schemes

为使超级电容的优势得以发挥，可以采用加入双向 DC/DC变换器的方式控制超级电容器的输出功率和电压。为进一步降低超级电容等效内阻，选择降低超级电容器组的电压等级，增加电容器并联支路，经过双向DC/DC变换器升压后，再与直流母线相连接的方式。目标船舶的储能系统结构如图3。

双向DC/DC变换器按结构类型可分为非隔离型和隔离型两种。隔离型双向DC/DC变换器结构复杂、电力元件多、控制复杂导致成本较高，功率密度较低，不适用于船舶的复合储能装置中。在非隔离式的Buck型拓扑、Boost型拓扑、Buck-Boost组合型拓扑三种拓扑结构中，Buck-Boost结构具有较小的电感和较低的开关导通损耗，效率也比另外两种更高，更符合纯电动船舶复合储能装置的需求，故选用双向Buck-Boost型变换器。双向DC/DC变换器匹配超级电容可以提供稳定的电压输出，与动力电池并联供电时，能够有效减少环流问题。

图3 纯电动船舶储能系统结构Fig.3 Structure of all-electric ship energy storage system

2 复合储能装置的多目标优化设计

纯电动船舶在储能系统的设计中，应综合考虑成本、功率限制、装置使用寿命、重量等多方面因素，因此该类纯电动船舶储能系统中复合储能装置的优化选型是一个多目标的优化问题。

采用第二代带精英策略的非支配排序遗传算法（NSGA-II），对船舶储能系统复合储能装置进行设备选型和优化配置，确定磷酸铁锂电池和超级电容的型号及串并联个数。

2.1 NSGA-II优化变量与目标确定

DEB教授等[8]在第一代遗传算法（NSGA）的基础上改进，得到第二代带精英策略的非支配排序遗传算法（NSGA-II）。相对于第一代遗传算法，第二代遗传算法具有降低计算的复杂度、提高优化结果的精确度及保证种群的多样性等优点。

采用NSGA-II优化算法对混合储能设备的容量配比进行选型，首先要确定优化设备参数量。表 4和表 5分别是磷酸铁锂电池和超级电容的备选参数，遗传算法中优化变量的相关参数见表6。

表4 电池备选参数表Table 4 Battery optional parameter list

表5 超级电容的备选参数表Table 5 Super capacitor optional parameter list

表6 优化设计变量的相关参数Table 6 Related parameters in the optimization design variables

将储能设备总价格、总重量和一个典型工况周期耗能作为优化目标，其数学表达式如下：

式中：fprice(X)、fenergy(X)、fweight(X) 分别表示储能设备总价格、一个典型工况周期消耗的总能量、设备总重量；X为储能设备的选型方案；tj≥ 0 为储能系统及纯电动船整体性能的约束函数。约束函数主要考虑：①最低容量约束；②超级电容荷电状态SOC约束；③最大瞬时功率约束。

2.2 仿真模型及变量传递

采用仿真的手段，使用Matlab/Simulink模块搭建纯电动船的能量消耗模型。并用该模型得到一个典型周期的能量消耗量。模型主要包括储能装置模块、负载模块以及能量管理模块。

在优化的过程中，NSGA-II算法优化与Simulink模型仿真交替进行，在使用sim命令时将simset设置中的SrcWorkspace和DsrWork2space的属性改为current，将仿真与算法的优化结合起来，自动传递算法与模型之间的变量。

2.3 选型优化结果

以纯电动船舶储能系统的总成本、设备重量和一个典型工况下的总耗电量为选型优化目标，设置种群规模为 50、进化迭代次数为 50、交叉概率为0.5、变异概率为0.1、染色体长度为5。

经过 NSGA-II算法迭代50次后，由于备选设备库容量相对较小，出现部分解的重叠现象，最终得到27个Pareto最优解，如图4所示。以设备的总价格最低为标准，选型最优的4个点在图中用箭头标出。4个Pareto的最优解见表7。

图4 选型最优解集分布图Fig.4 Distribution diagram of the optimal solutions

表7 选型最优解集Table 7 The optimal solutions

在选型策略中，首要考虑的是价格目标。方案1的价格最低，但由于方案1中电容串联的个数过多，可靠性较差；方案2价格与方案1相差并不多，且耗电量相对较低，重量也在可以接受的范围内。综合考虑，确定方案2为最佳选型方案。

3 能量管理模糊控制策略

为了充分发挥超级电容功率密度大的优势，设计了一种基于滤波器的模糊逻辑控制器。如图5所示，负载功率的需求先通过低通滤波器的滤波作用，分离出功率需求中的高频负载Pt、低频负载Pr。

图5 能量管理系统示意图Fig.5 Schematic diagram of energy management system

选择的低通滤波器为：

式中，Ld(s)为传递函数，T0为时间常数。根文献[9]中的评价公式，试验不同的低通滤波器的滤波效果，滤波时间常数为18时结果较为满意，所得到的滤波效果如图6所示。图中，低频部分中分配给电池承担的负载功率仍然有较高的功率需求，而此时高频部分负载功率并不大，所以在滤波器后又设计了模糊控制器来进一步处理低频部分。

模糊控制流程是先将输入变量进行模糊化处理，之后进入预先设定的知识库，进行模糊推理处理，输出模糊的变量，最后对输出的模糊变量进行解模糊化处理，得到精确输出[10]。

模糊控制器的输入分别为滤波后船舶的功率需求Pr、电池模块的荷电状态SOCb、超级电容模块的荷电状态SOCc，输出为超级电容模块的功率分配因子Kc。定义Kc为超级电容模块所提供的功率占功率需求的比例。

根据图6中低频功率需求图谱，确定功率需求的范围为[0, 100]，将其划分为4个子集Pr= { TS、S、M、B}；基于磷酸铁锂电池的工作原理和特性，确定SOCb在[0.3, 0.9]之间，将其划分为3个子集SOCb={L、M、H}；基于超级电容的工作原理和特性，通过双向DC/DC变换器对超级电容进行升压控制，扩大了超级电容的工作电位窗，其正常的工作范围为[0.2, 0.9]，同样分3个模糊子集SOCc= {L、M、H}；Kc的基本取值范围为 [0, 1]，分为4个模糊子集Kc={TS、S、M、B}。

各隶属度函数如图7所示，最后写入制定的模糊规则，按照规则输出变量。

图6 滤波器滤波效果图Fig.6 Filter effect diagram

图7 隶属度函数Fig.7 Membership degree functions

4 仿真分析

在Matlab/Simulink中搭建目标船舶的电力推进系统模型，模型主要包括电池模块、超级电容模块、双向DC/DC变换器模块、能量管理模块和负载模块五个部分。该模型中电池模块和超级电容模块采用2.3中的选型优化方案。

仿真模型的功率输入为图2所展示的典型工况的功率图谱。电池和超级电容分配的功率如图8所示。可以看出，在0 ～ 85 s和200 ～ 350 s的定速航行工况时，超级电容的充放电功率近似为 0，主要由电池承担复合储能装置的功率需求；在85 ～ 200 s的机动航行工况，复合储能装置中的低频功率需求由电池承担，高频功率需求由超级电容承担；图8b超级电容功率曲线中的负值部分，为负载功率需求不大时，电池向超级电容充电，为超级电容下次放电应对瞬态加速工况做准备。功率增强因子γ最大为 2.34，表明储能装置经过优化选型并结合模糊控制的能量管理策略能在磷酸铁锂电池和超级电容间合理分配功率输出，较好地应对波动性负载，达到保护电池组的目的。

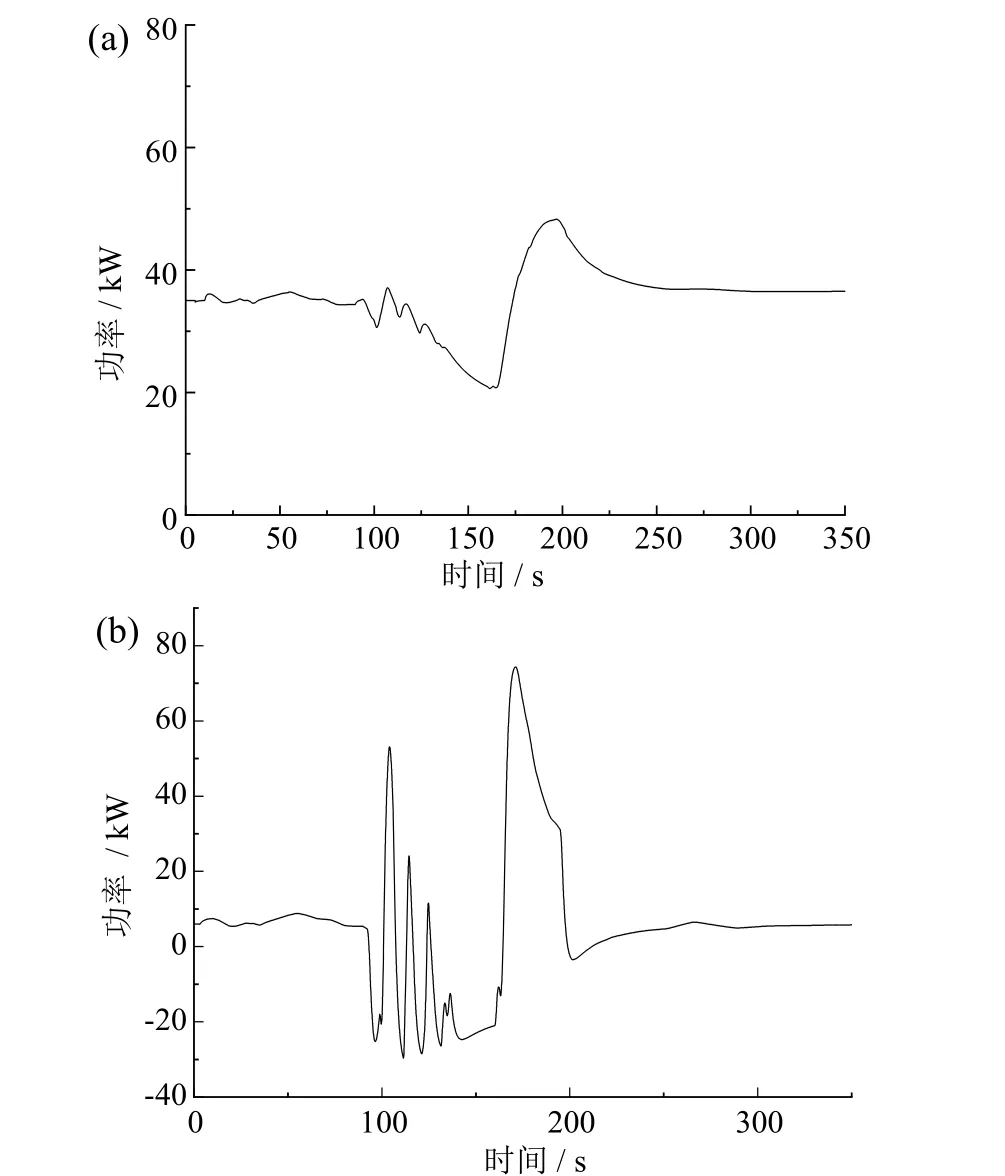
图8 （a）电池和（b）超级电容功率分配图Fig.8 Power distribution diagrams of (a) the battery and (b) the super-capacitor module

5 结 语

对100客座纯电动船舶的储能系统进行计算论证，选择采用核心元件由锂电池、超级电容和DC/DC变换器组成的复合储能装置为动力源，采用遗传算法对元件进行了多目标优化选型配置，并提出了能量管理策略。搭建仿真模型，利用典型工况功率需求作为输入，对选型结果进行验证分析。结果表明，所述的选型方法选出的配置方案，结合能量管理策略，能够满足船舶的典型功率需求。