浅海沉积层探针测量系统

孙浩添，黄楷伦，孟艳丽，王连明，吴金荣

(1.东北师范大学物理学院，吉林 长春 130024；2.中国科学院声学研究所，北京 100190)

0 引言

浅海是现阶段人类海洋活动的主要区域，搭建海上钻井平台、水产养殖、铺设海底光缆等海洋作业都需要了解浅海沉积结构.传统测量海底沉积结构的方法操作复杂、耗时长、受海洋环境影响严重，因此，迫切需要一种能够快速、准确获得海底沉积结构的仪器[1].国外研发了多普勒式探针[2]、多波速测深探针[3]、枪插入延迟计[4]等多种基于不同原理的探针.其中多普勒式探针与多波速探针依靠声学原理进行测量，测量范围广，但由于水声性质的影响，精度逊色，价格昂贵，不利于进行大规模投放与阵列式测量；枪插入式探针依靠力学原理进行测量，精度较高，但结构复杂，成本高，且受到最小插入深度的限制，不利于在浅海区使用.国内浅海探测技术主要依赖于国外产品，不但价格昂贵，而且在使用过程中受到国外技术制约.[5-6]

因此需要设计一种针对水下20～200 m浅海沉积层测量系统[7].它通过采集探针与沉积层撞击加速度的变化，计算被测沉积层弹性模量，从而建立基于弹性模量的浅海沉积层结构定性的分类方法.[8-10]从系统建模与机械结构、信号采集与数据传输综合考虑，设计探针测量系统，并通过与已知弹性模量的软黏土比对，进行性能测试.最后根据实测结果建立基于弹性模量的浅海沉积层定性分类方法.在浅海沉积层测量方面，浅海沉积层探针测量系统与传统测量方法相比，成本低廉，受海洋环境影响小，是一种快速远距离定性测量方法；与其他探针系统相比，抗干扰能力强，不受插入深度的影响，并且建立了利用浅海沉积层探针系统测量，基于弹性模量的浅海沉积层定性分类方法.

1 系统建模与机械结构

由海面以自由落体方式下投的探针，下落过程中受到重力、浮力、海水的阻力作用，在发生碰撞前，需探针达到匀速运动状态.因此可以得到匀速运动状态下的简化运动方程为

(1)

其中：m为探针质量，g为常数，c为海水的阻力系数，v为探针碰撞前的速度，s为探针截面积，B为探针所受的浮力.

如果要保证探针碰撞前匀速阶段速度为5～7 m/s，取海水对探针的阻力系数为0.25～0.4，海水的密度近似为1.03×103kg/m3，则可估算探针的质量；根据探针所用材料，可以确定探针的体积.

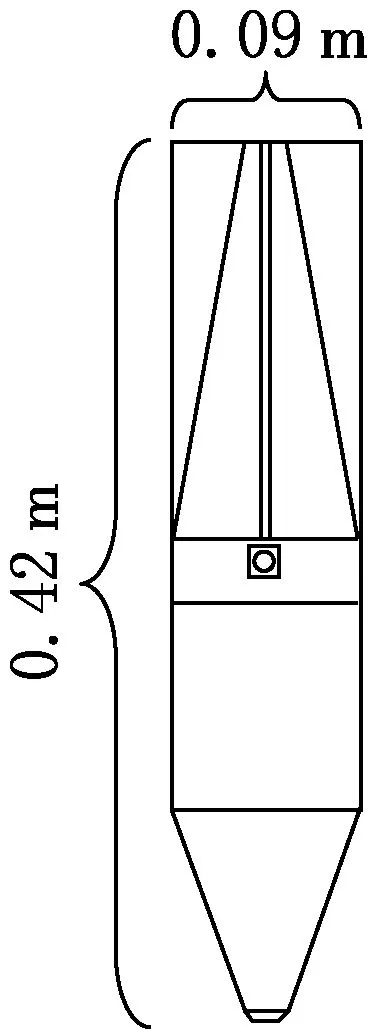
图1 探针外观

最终探针设计为体积为9.69×10-4m3，直径为9×10-2m，高度为0.42 m的近似圆柱体，如图1所示.

质量m约为5.05 kg，探头为合金钢，尾翼为轻质铝.可实现探针碰撞前v的范围为5.5～6 m/s.

实际撞击过程可以近似为完全非弹性碰撞的球板模型，探针相当于球体，沉积层相当于板，计算公式为[11]

(2)

其中：μ1，μ2分别为撞击双方各自的泊松系数；E1，E2分别为撞击双方的弹性模量；R为探针的等效半径；m为探针的质量；v为探针碰撞前的速度；t为碰撞持续时间，t不包含探针回弹时间.

实际沉积层情况是多变的，可以将其抽象为饱和但弹性模量不同的黏土进行加速度范围的计算[12].

极端软的情况：取饱和很软黏土作为模型，即缝隙被水填满的很软黏土，泊松比为0.5，弹性模量为0.30～0.35 MPa；合金钢的泊松比为0.25～0.3，弹性模量为205 GPa；探针质心到前端的等效半径R为0.05 m.由此计算出碰撞时间的最大值为0.020 8 s.将碰撞理解为瞬时过程，平均最大加速度为265.7 m/s2.

极端硬的情况：取饱和沙质黏土作为模型，即缝隙被水注满的沙质黏土，泊松比为0.5，弹性模量为30～40 MPa；合金钢的泊松比为0.25～0.3，弹性模量为205 GPa；探针质心到前端的等效半径R为0.05 m.由此可计算出碰撞持续时间的最小值为0.002 8 s.将碰撞理解为瞬时过程，平均最大加速度为2 493.818 m/s2.

实际被测的湖底或海底沉积层，其撞击时间与加速度应该介于上述两种极端情况之间.

2 信号采集与数据传输

信号采集与传输系统分为水下采集单元与水上甲板单元，水下采集单元负责信号采集，内部搭载采集电路.甲板单元负责信号的接收与处理，由接收器和处理器构成(见图2).

由于是定性分析，在撞击持续时间内采集的数据点的数量，以能绘制不失真的撞击曲线为宜，因此可根据撞击持续时间确定传感器的采样频率.根据推算的最大平均撞击加速度确定传感器量程.在同样采样位数的情况下，量程选取较小将导致测量范围减少，量程选取过大将导致测量精度降低，因此综合上述因素，选择加速度传感器ADXL375，它的量程为-2 000～2 000 m/s2，最高采样频率为3 kHz.

水下采集单元由STC单片机作为主控制器，甲板单元的接收器由STM32F207单片机作为主控器[13]，通过RS-485通信协议完成数据传输，处理器为PC机，如图3所示.

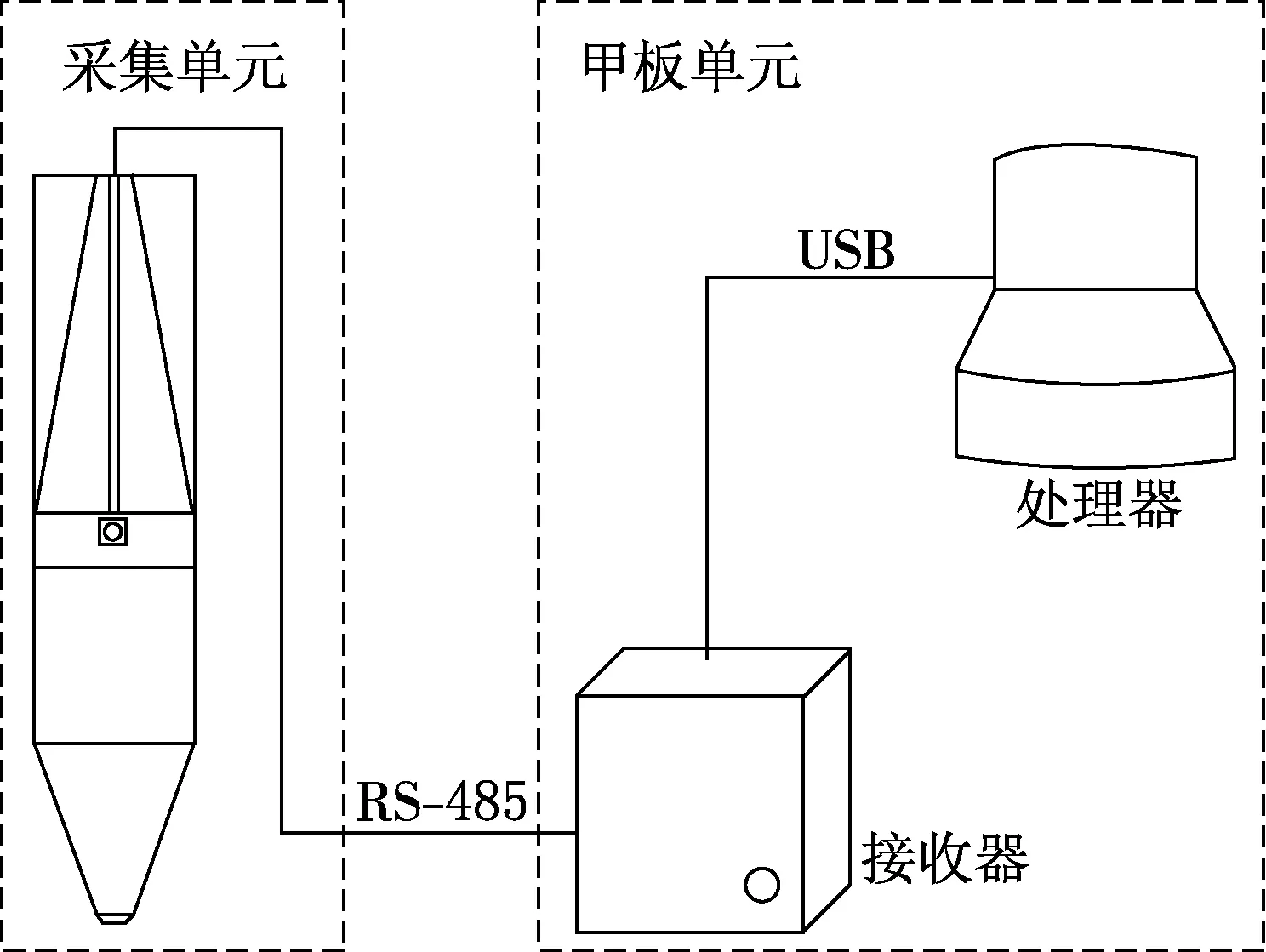
图2 采集与传输系统

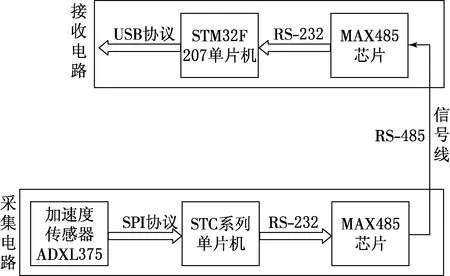
图3 采集与传输电路

3 性能测试

首先，在已知水下沉积层类型的湖泊采用本系统，采集撞击加速度数据并绘制加速度曲线，形成标准样本，然后对未知沉积层类型的海底进行测试.

图4是撞击沉积淤泥的加速度变化曲线，横轴表示时间，纵轴表示加速度，曲线的形状则与待测沉积层特性有关，能够定性反映沉积层特性.[14]

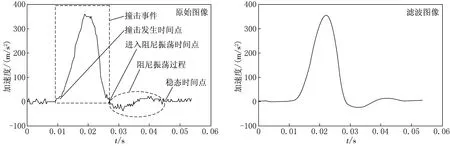
图4 沉积淤泥的加速度曲线

曲线中有3个关键的时间点和2个重要过程：

撞击发生时间点：探针自由落体下落后撞击开始的时间点，在实际测量中这点很难捕捉的到，因此是一个近似点.

撞击事件过程：加速度由0开始向数轴正方向增大到峰值并随后减小到0的时间区域.在这个区域中，探针的加速度是由0逐渐增大至峰值随后逐渐减小至0，曲线的形状与沉积层的结构有关.

进入阻尼振荡时间点：探针在撞击时间后，由此点进入阻尼振荡过程，这一点即是探针的加速度第2次为0的时间点.

阻尼振荡过程：阻尼振荡过程的强度与沉积层的性质有关.探针测量数据中阻尼振荡阶段的分析，对浅海沉积层强度相关研究人员以及海洋地理学和地声学人员具重要的意义[15].

稳态时间点：探针的阻尼振荡过程结束，最终进入合加速度为0的稳态.

滤波后的图像与原始图像非常相似，这说明采样所得的加速度几乎是平滑连续的.这是因为实测事件中，在相同采样频率的情况下，越是相对平缓的撞击过程，采样点越能较好地描述加速度变化.

图5是撞击淤泥与细沙混合物的加速度变化曲线.由于含有细沙，图5更加松散.由图5中可以看出，加速度的峰值较低，形状与图4过程类似，阻尼振荡的过程略有不同.这种相似性是由于同样的沉积淤泥造成的.不同则是因为区域混有少量的细沙.

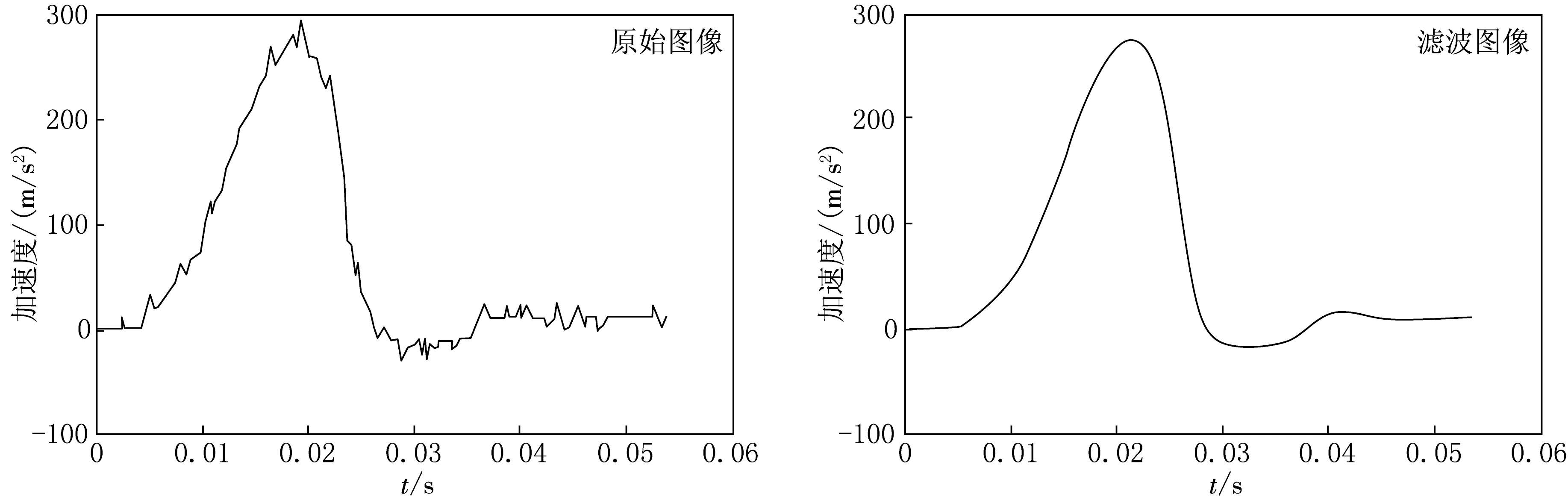
图5 撞击淤泥与细沙混合物的加速度曲线

图6是撞击硬质沙土的加速度变化曲线，由于水分蒸发，沙土已经略微板结成块.由图6可以看出，加速度的峰值较大，曲线形成了一个尖峰.而且曲线无阻尼振荡事件，加速度以一个过阻尼过程直接降低至稳态.

图7是在辽宁老铁山海湾对水下沉积层的测试结果，老铁山海湾水下80 m深区域为老铁山余脉，以大块光滑岩石为主.因此从图7可以看出，加速度的峰值超过了100 m/s2.本次采集到的加速度已经不能看做是一个平滑连续曲线.但在实际中加速度值是不能突变的，原因在于传感器的采集频率偏低，快速变化的信号导致采样点过少造成的.

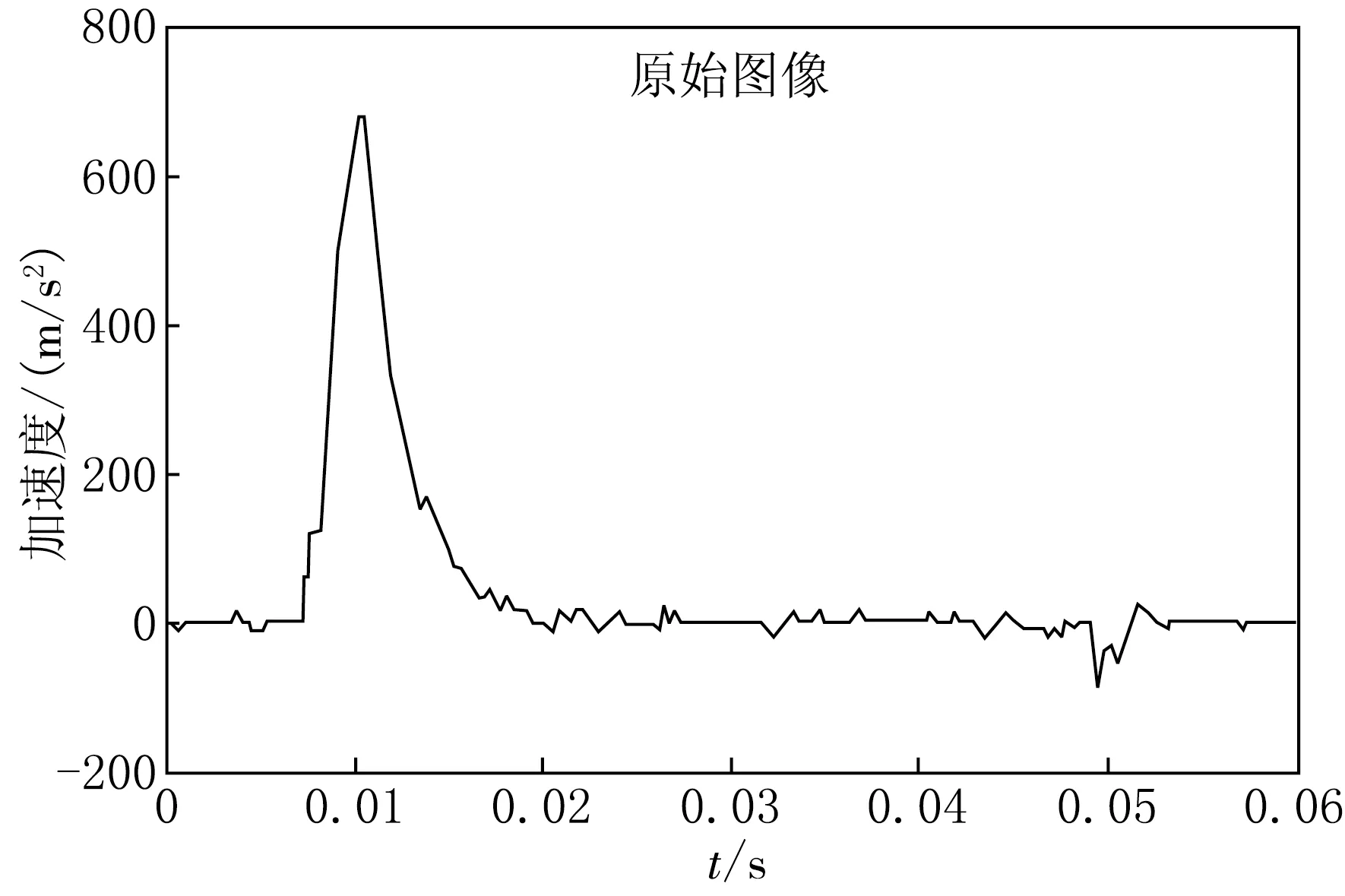
图6 撞击硬质沙土的加速度曲线

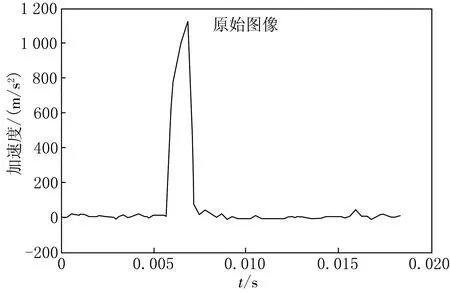
图7 老铁山海湾的测试结果

4 沉积层的定性分类方法

综上所述，并结合数学模型中的(2)式采用弹性模量对沉积层进行定性分类.在一次撞击事件中，若探针的形状、材质及质量已确定，即探针等效半径R、前端材质泊松比μ1、弹性模量E1、探针整体质量m已确定，则碰撞持续时间t是由撞击速度v、待测物泊松比μ2、待测物弹性模量E2决定的.

根据(2)式可推导出

(3)

其中对于传统材料，在弹性工作范围内，泊松比一般为常数，但超越弹性范围以后，泊松比随应力的增大而增大，最大值为0.5.碰撞持续时间t和撞击速度v可根据撞击曲线进行确定，因此，根据(3)式计算出弹性模量E2.

通过将待测物的弹性模量E2与已知标准样本的弹性模量进行比较，定性地对待测物进行分类.在当前采样频率下，且不严重失真的前提下，根据撞击事件时间，计算出探针可测饱和沉积层的弹性模量范围.

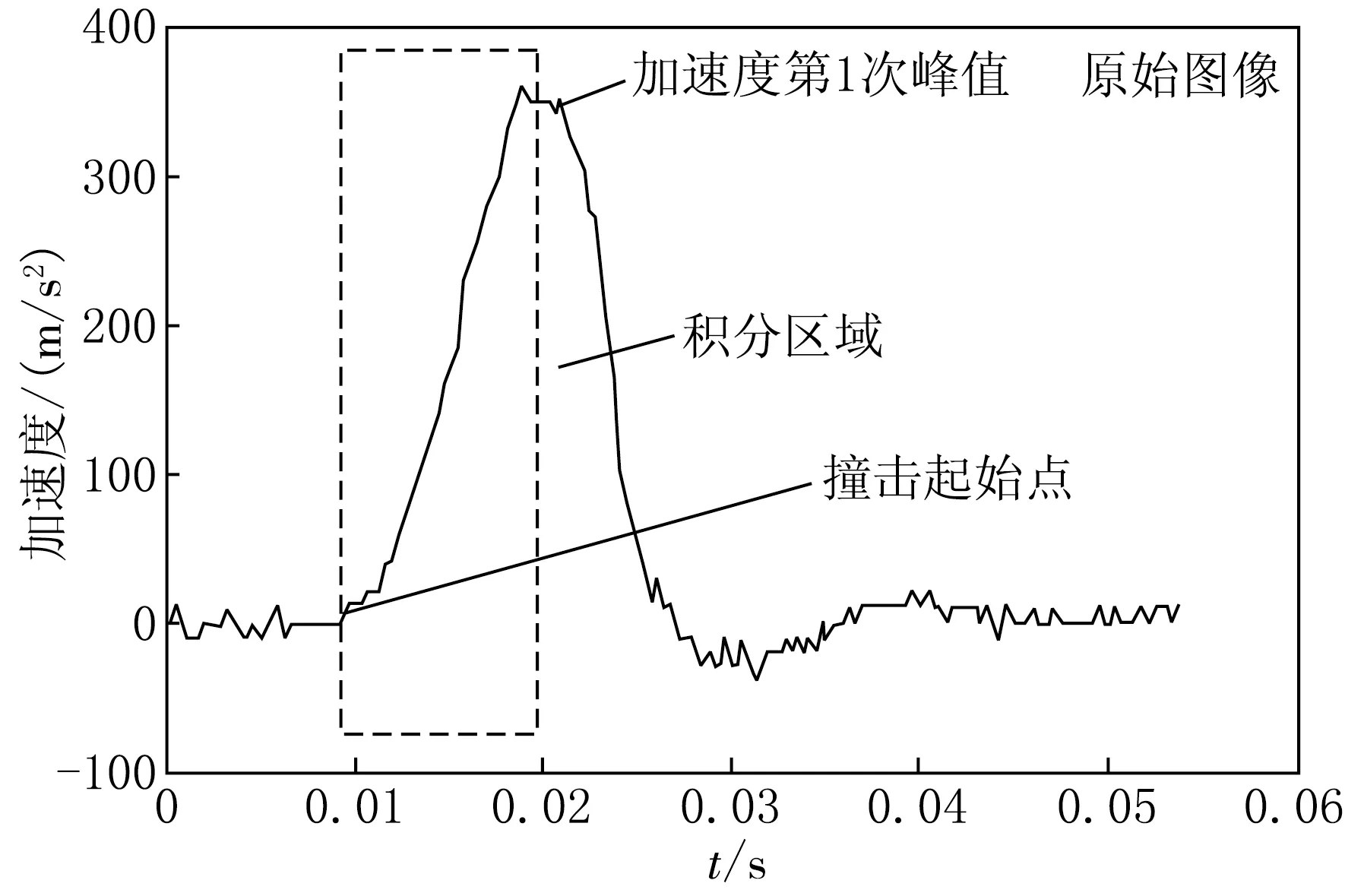
图8 计算撞击速度的积分区域

以图4为例说明计算方法.图4中探针处于正常工作状态，撞击过程可等效为一个有阻尼的弹簧振子振荡过程，所以对图4的数据进行如图8的积分，积分结果近似为探针的撞击速度v=1.59 m/s，计算碰撞时间为0.009 3 s，弹性模量为4.13 MPa.经过查询黏土的弹性模量表，可以得知饱和软的黏土弹性模量为4～5 MPa，可见沉积淤泥的弹性模量与饱和软黏土相似.

对各种已知沉积层进行测试，测定的撞击速度、第1次达到峰值时间及计算的弹性模量结果见表1.

取撞击速度为表1中撞击速度平均值1.87 m/s，将其作为v代入(3)式可以得到碰撞时间t与弹性模量E的关系，如图9所示.

由数学模型可知，所讨论碰撞时间并未包含回弹过程.因此，第1次达到峰值的时间即为数学模型中的碰撞时间，将碰撞前的速度和相应的第1次达到峰值时间代入数学模型，计算出相应的弹性模量，绘制在图9中，以星号表示各测量点.

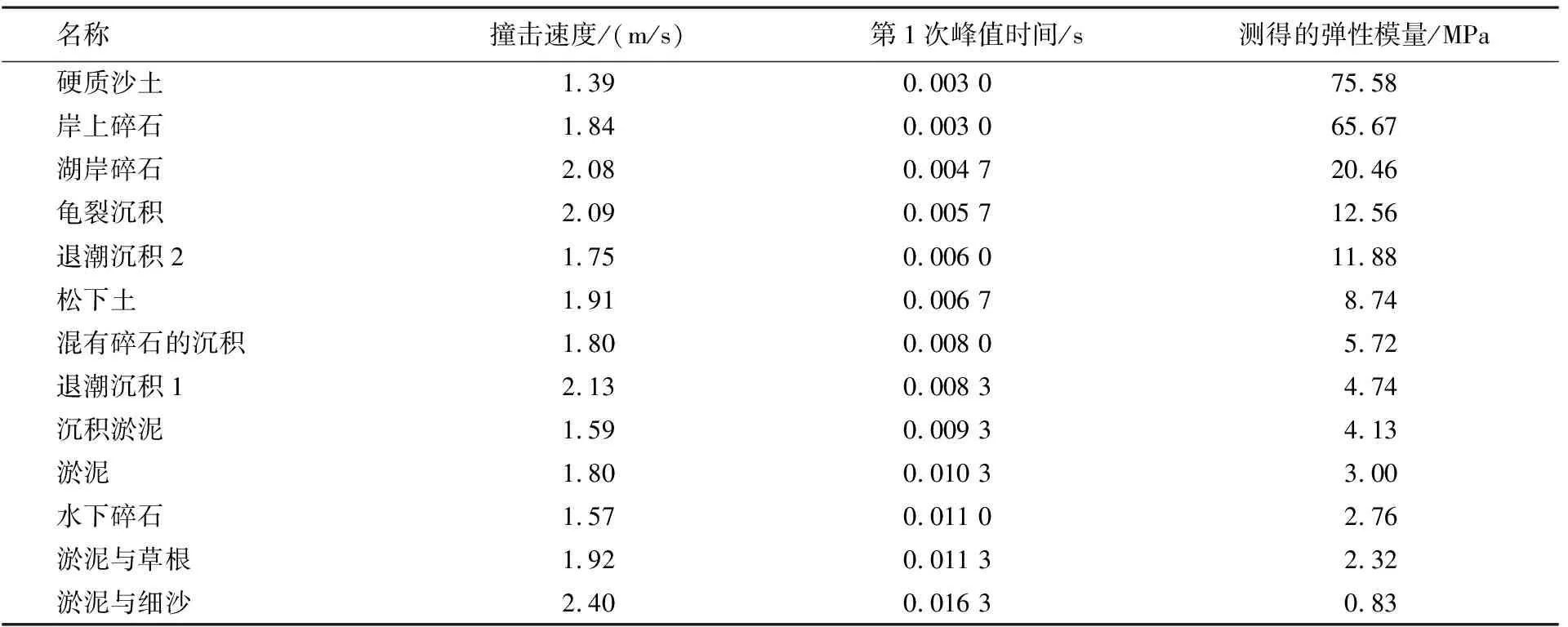
表1 相同高度测量不同待测物的弹性模量

由图9中可以看出，通过估算所得弹性模量变化趋势基本符合理论模型中的固定速度下的弹性模量变化趋势.其中撞击时间小于0.004 7 s(左侧第3点)，传感器已经失真，无法再正确地描述加速度变化，因此本文设计的探针系统可测饱和沉积层的弹性模量范围应小于20.46 MPa，且大于传感器噪声门限.在其可测范围内，可以根据弹性模量对待测沉积层进行定性分析.

对同一实验对象，进行了3组重复实验，将测得叠加曲线绘制在图10中.

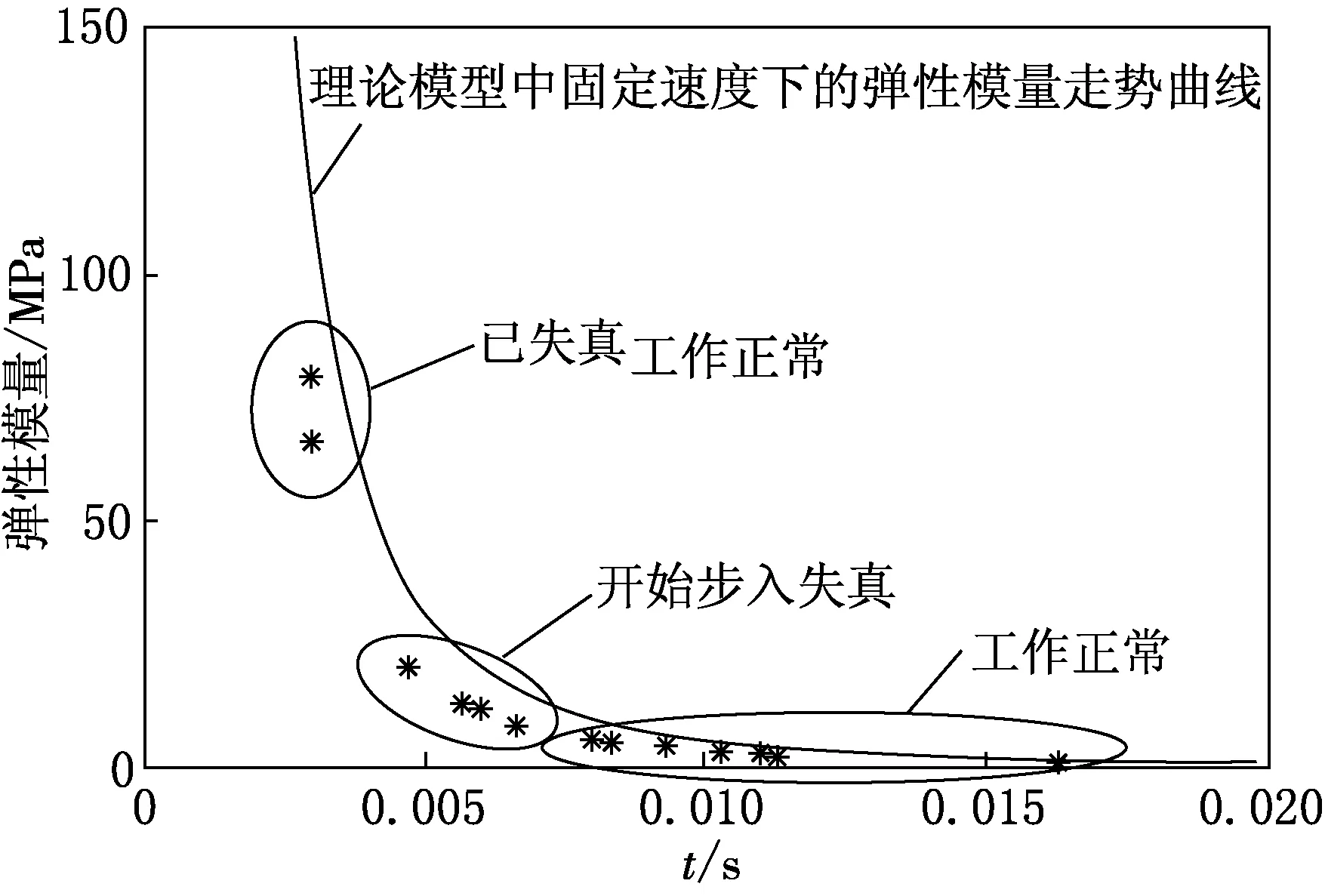
图9 测得弹性模量与理论计算弹性模量

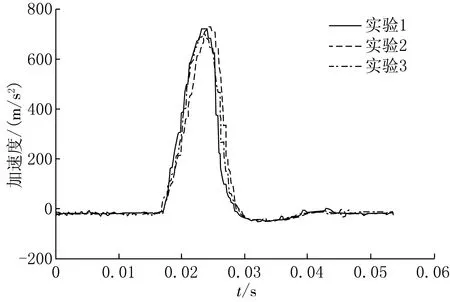
图10 3次重复实验叠加曲线

3组重复实验所测曲线能够很好地叠加在一起.这说明了探针对于同一待测对象，具有很好的可重现性.

5 结果与讨论

对于不同的待测沉积层，在探针不失真的情况下，所产生的阻尼振荡过程与沉积层的性质有关，根据撞击阻尼振荡的曲线可确定弹性模量，根据弹性模量在泊松比接近0.5的情况下，对待测物进行定性分析.

从探针本身来说，探针采样频率为3 kHz，能有效检测加速度小于200 m/s2的撞击事件，下限为传感器的噪音门限.

从待测沉积层来说，在沉积层弹性模量小于20.46 MPa的范围内，探针工作正常，在沉积层的弹性模量大于 20.46 MPa时，探针开始失真.

数学模型中的理论收尾速度与积分所得的速度相差较大，这是因为数学模型中的板是理想的，不会因为撞击而发生挤压、变形、移动.而实际撞击过程，在探针撞击土壤时，土壤会被挤压、变形、移动.因此，实际过程中采集到的加速度传感器事件的积分并不能完全表示探针达到收尾速度.受撞击事件影响的土壤的总质量越大，则积分所得速度与探针匀速运动时的收尾速度相差就越远.

为使探针测量更准确，可从以下两个方面进行改进：

(1) 提高传感器的采样频率.更高的采样频率可以更真实地描绘撞击事件.

(2) 因地制宜，针对不同的待测结构，采用不同的探针.比如本文中的传感器量程之所以选择如此之大，是因为在大范围内浅海沉积层整体结构复杂多变.因此，可先用量程较大、采样频率较低的探针进行粗测，然后再使用量程较小、采样频率较高的探针做更高精度的测量.