复杂管路油水两相流动的统一机理模型

2019-01-02赵麟汪志明曾泉树

石油科学通报 2018年4期

赵麟，汪志明，曾泉树

1 胜利石油管理局博士后科研工作站，东营 257001

2 中国石油大学(北京)石油工程学院，北京 102249

0 引言

石油行业中的复杂管路通常由各种不同的管道和管件通过串联或并联组合而成，在开采和运输过程中，油水两相和油气水多相混合流动是其中最常见的流动形式[1-3]。多相流系统内的结构及分布具有不均匀性，状态具有非平衡性和多值性，且各相间存在可变形相界面。相界面及其引发的特征受各相流体的流体参数、管道几何参数等因素的影响，流动十分复杂，理论研究工作面临着很大的困难。随着我国对西部沙漠油田和东部海上油田开发需求的进一步增大，对油水两相和油气水多相流动规律的研究显得更加迫切[4-6]。

油水两相流研究是油气水多相流研究的基础，深入研究油水两相在复杂管路中的流动规律，特别是分流情况和压降规律，既可解决石油生产过程中的重要问题，同时对完善多相流理论具有重要意义。徐道振等[7]对国内外水平管内的油水两相流流型进行了总结，并给出了流型划分和转换的准则。郭松林等[8]研究了页岩气在水平井中的流动，通过Fluent模拟了水平井筒中气水两相的流动规律。Hana fi zadeh等[9]对倾斜管中的油水两相流型进行了研究，发现了管道倾角对流型过渡边界的影响规律，并指出上升流中非分层流(如泡状流、段塞流)占主导地位，下降流中分层流占主导地位。Pouraria等[10]利用计算流体力学模型研究了两相流在井下不同工况下的流型，数值模拟结果和已有实验数据吻合良好。Han等[11]发现压差法是预测油水两相在低流速、高含水率情况下流速的最有效方法，基于流型划分准则和持水率，利用漂移模型预测了单相的表面速度。Karami等[12]结合气液两相流模型和油水两相混合模型，得到了水平管中油气水三相流动模型。Zhai Lusheng等[13]开展了水平井筒小直径圆管中的油水两相流动实验。Pietrzak等[14]研究了垂直管中油气水三相流动规律，给出了油气水三相上升流压降计算的新方法。

尽管国内外学者对油水两相流流型转变[15]、压降预测[16]、反相规律[17]等进行了大量的实验和理论研究，但这些模型都只在一定范围内具有较高的精度，通用性较差，没有成熟的统一理论模型。目前对油水两相流动的研究主要局限于单一恒径管道内，而复杂管路中的油水两相流动仍有待进一步研究。本文基于管路串并联理论、流型转变准则、双流体模型和均相流模型。建立了复杂管路油水两相流动的统一机理模型，通过实例对该模型进行了验证，并与数值模拟结果对比，分析了油水混合物在不同油相黏度和含水率下的分流情况，对其压降进行了预测。

1 模型构建

本文中油水两相分层流动考虑了油水纯分层(O &W)，上层油包水下层纯水的拟分层(W/O & W)，上层油包水下层水包油的拟分层(W/O & O/W)和上层纯油下层水包油的拟分层(O & O/W)这4种流型。油水两相分散流动考虑了油包水(W/O)和水包油(O/W)这两种流型，如图1所示。

模型的基本假设为：(1)油、水均为牛顿不可压缩流体；(2)流体与外界无热传导或做功现象，系统处于等温流动状态；(3)稳定流动；(4)油水界面假设为平面；(5)不考虑各管道和管件之间的相互作用；(6)不同通道的流体性质保持一致。

1.1 流型转变准则

由于油水密度差较小，其界面张力较低，油水界面易发生波动，转化为其他流型。而从分层流到分散流的转换主要取决于连续相总湍动能和分散相总自由能之间的平衡关系。若湍动能较大，分散相将以球形液滴形式分散在连续相中，并在湍流运动下相互碰撞，产生融合。如果液滴尺寸过大，在湍流力的作用下，液滴会破裂。因此，每个流动单元所能包含的最大分散相量取决于连续相的湍流强度。根据Atmaca的研究[18]，当油水混合液流速大于某一临界值时，流体会从油水两相分层流转变为油水两相分散流。另外，分散相的液滴融合和连续相的破碎可能导致系统出现反相现象，反相时系统的界面自由能最大。根据王玮和宫敬的研究[17]，如果分散相体积大于临界体积，分散相将转为连续相。

图1 油水两相流型转换示意图Fig. 1 The transformation diagram of oil/water two-phase fl ow patterns

其中，vm为混合液流速，m/s；Ce为倾斜系数，无量纲；ηd为分散相体积含率，无量纲；σo/w为油水两相表面张力，N/m；ρw为水相密度，kg/m3；ρo为油相密度，kg/m3；g为重力加速度，m/s2；fm为混合液壁面摩擦系数，无量纲；ρm为混合液密度，kg/m3；ηw为水相体积含率，无量纲；ηo为油相体积含率，无量纲；ηcr为临界体积含率，无量纲。

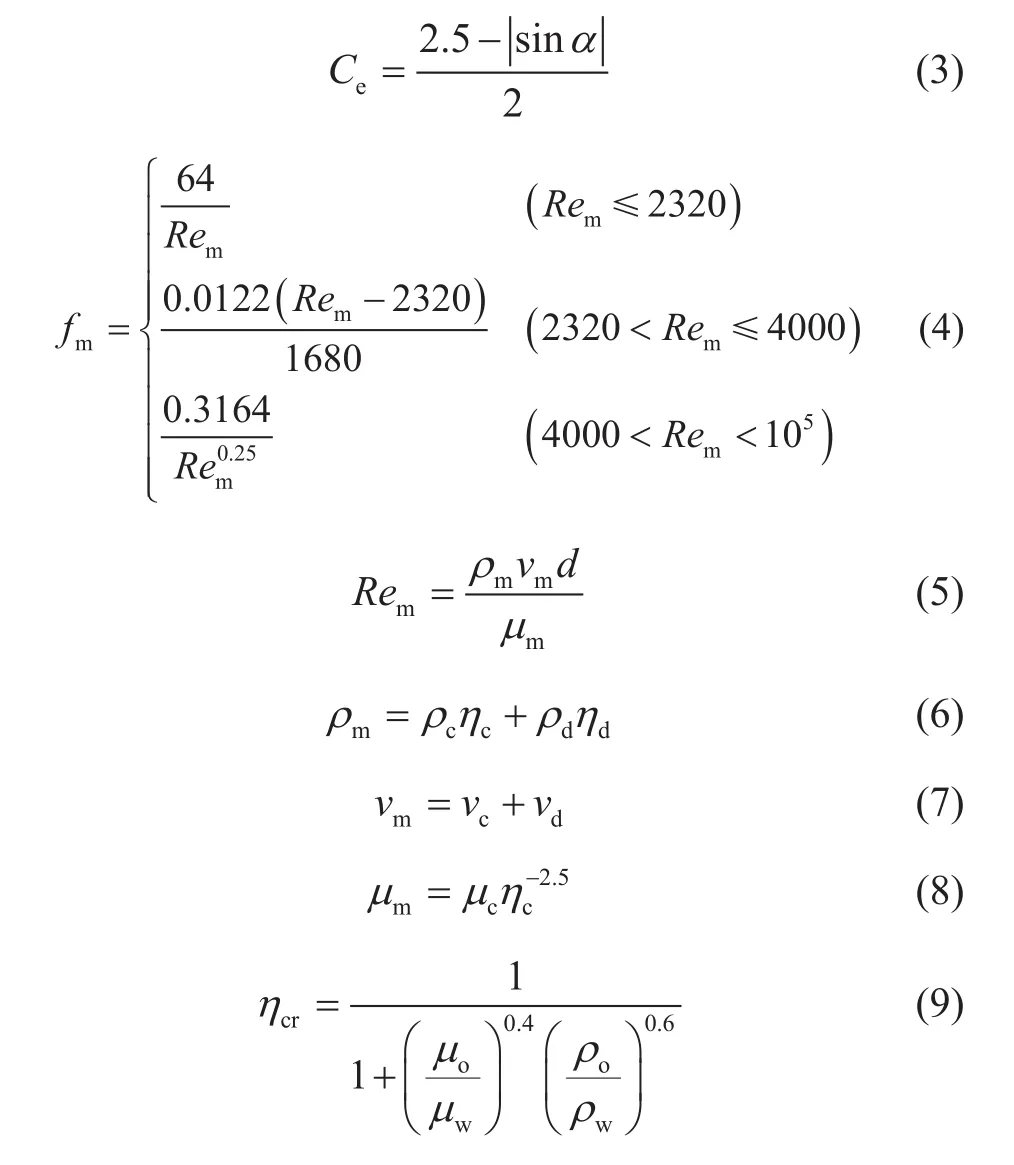
其中，α为管道偏离水平角，°；Rem为混合液雷诺数，无量纲；d为过流面积直径，m；µm为混合液黏度，Pa·s；ρc为连续相密度，kg/m3；ρd为分散相密度，kg/m3；vc为连续相流速，m/s；vd为分散相流速，m/s；µc为连续相黏度，Pa·s。

图2 水平管道油水两相流动控制体示意图Fig. 2 Control volume of oil-water two-phase fl ow in the horizontal pipe

1.2 流体在水平管道中的流动

水平直管中油水两相流动的控制体如图2所示。水平直管油水两相分散流动模型是基于均相流模型建立的，列动量平衡方程，如式(10)所示

其中，τm为混合液与井筒壁面的摩擦应力，Pa。

对式(10)进行积分，可得水平直管油水两相分散流动的通用压降方程。

其中，L为水平直管的长度，m。

流体从分散流动转变为分层流动时会发生分层现象，上述方程不再适用，需要基于双流体模型重新对压降方程进行推导。由于O & O/W、W/O & W和O &W这3种流型是W/O & O/W的特殊情况，因此本研究仅介绍W/O & O/W的建模过程。

对上层油包和水下层水包油的拟分层流动，分别列W/O层和O/W层的动量方程，如式(13)和(14)所示

其中，A1、A2分别为W/O层和O/W层所占的管道横截面面积，m2；p为x截面处的平均压力，Pa；τ1、τ2分别为W/O层和O/W层与井筒壁面的摩擦应力，Pa；S1、S2分别为W/O层和O/W层的润湿周，m；τi为油水两相分层流动的W/O层与O/W层的界面摩擦应力，Pa；Si为W/O层与O/W层的截面弦长，m。

将式(13)和(14)相加并进行积分，可得水平直管油水两相分层流动的通用压降方程。将式(13)和(14)相减并消去压力梯度项，可得水平直管油水两相分层流动的联合动量方程。

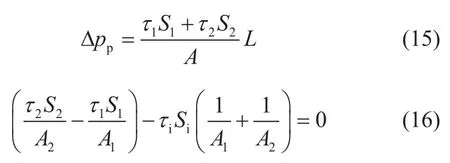
基于流体力学理论，结合图2中的控制体，则油相和水相的体积流量可分别表示如下。

其中，Qo、Qw分别为油相、水相的体积流量，m3/s；v1、v2分别为W/O层、O/W层的实际流速，m/s；αw1、αo2分别为W/O层、O/W层的分散相浓度，无量纲。

然而，要使上述模型封闭仍需确定几个关键参数，包括截面几何参数、摩擦应力参数和分散相含率参数。

截面几何参数包括上下两层的润湿周和横截面积。油水两相分层流动时，上下两层的润湿周分别如式(19)和(20)所示，而横截面积分别如式(21)和(22)所示

其中，γ为下部O/W层的湿周所对应的半弧度，无量纲。

同样可得W/O层与O/W层的截面弦长。

摩擦应力仍然引用摩擦系数的公式进行计算。

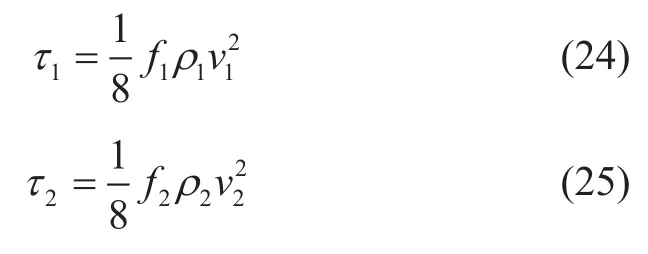
其中，

其中，f1、f2分别为W/O层和O/W层的Moody型壁面摩擦系数，无量纲；ρ1、ρ2分别为W/O层和O/W层的有效密度，kg/m3。

油水两相分层流动上下两层的有效雷诺数分别如式(30)和(31)所示。

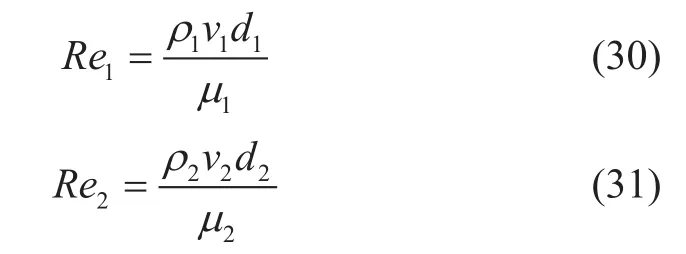
其中，d1、d2分别为W/O层和O/W层的水力直径，m；µ1、µ2分别为W/O层和O/W层的有效黏度，Pa·s。

油水两相分层流动W/O层和O/W层的水力直径根据各层的流速不同，计算公式亦有所不同[5]。

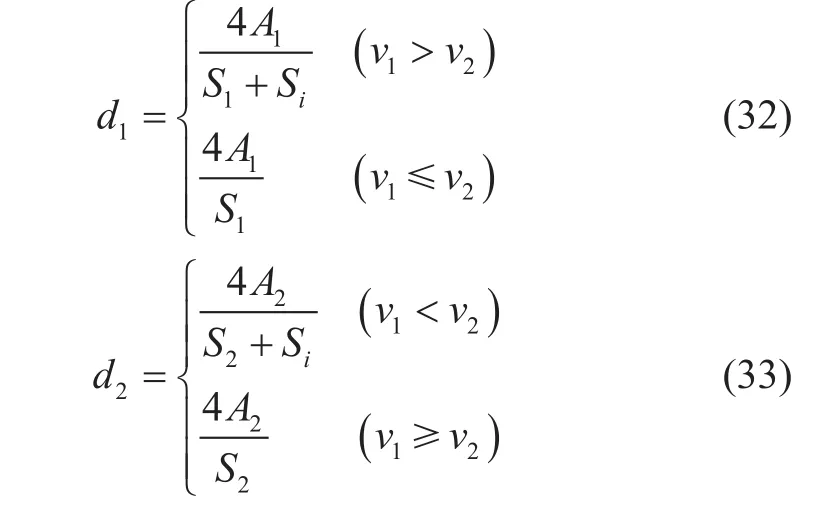
运用Roscoe-Brinkman公式计算W/O层和O/W层的有效黏度[19]。

1.3 流体在弯管中的流动

弯管中油水两相流动的控制体如图3所示。与水平管道油水两相流动相似，沿径向对压力梯度方程重新积分即可分别求得弯管中油水两相分散和分层流动的通用压降方程。

其中，R为弯管的弯曲半径，m；θ为弯管的弯曲弧度，rad。

1.4 流体通过突扩接头的流动

突扩接头油水两相流动的控制体如图4所示。忽略摩擦应力和重力，并且假设上下两层不发生质量交换。

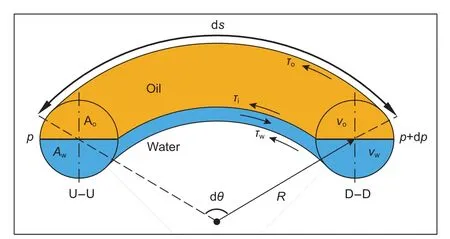
图3 弯管油水两相流动控制体示意图Fig. 3 Control volume of oil/water two-phase flow in the elbow

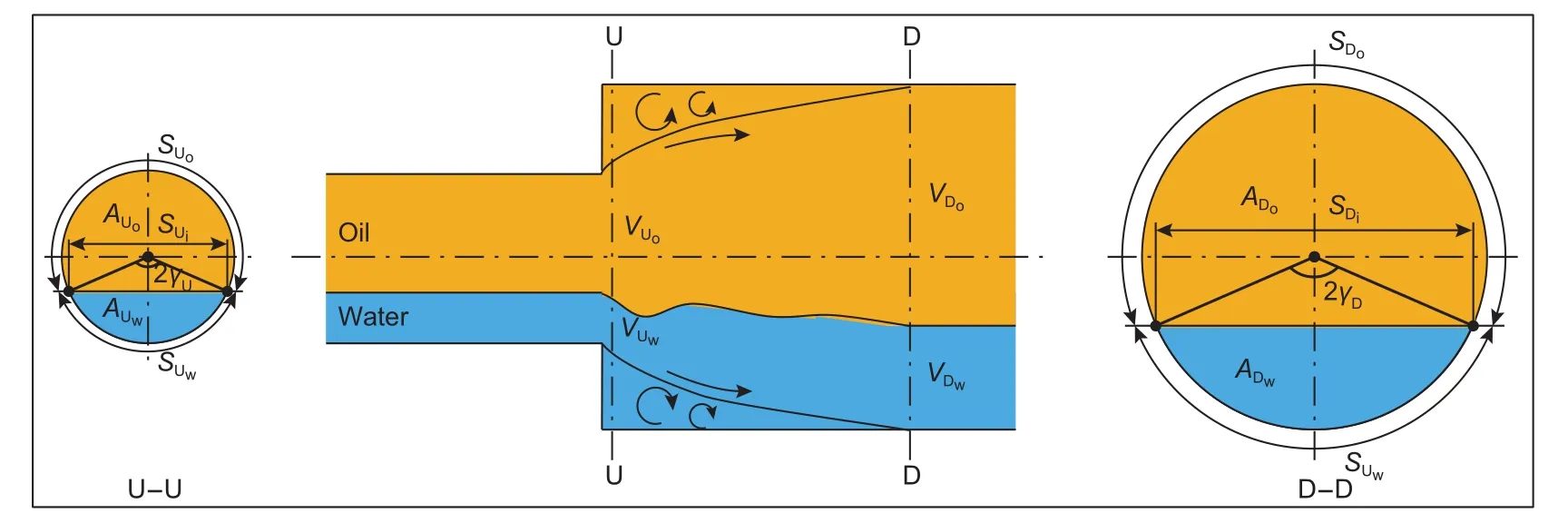
图4 突扩接头油水两相流动控制体示意图Fig. 4 Control volume of oil-water two-phase fl ow in the sudden expanded fi tting

基于均相流模型可建立突扩接头油水两相分散流动的通用压降方程，如式(38)所示。

相似地，流体从分散流动转变为分层流动时会发生分层现象，上述方程不再适用，基于双流体模型重新列出突扩接头油水两相分层流动的动量方程。

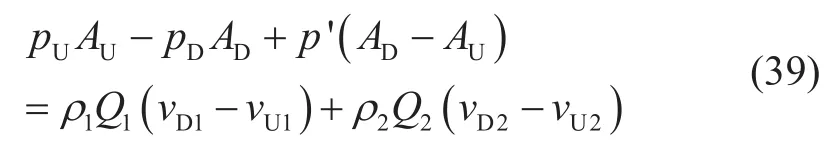
其中，Q1、Q2分别为W/O层和O/W层的流量，m3/s。

根据车得福的研究可知[2]，U-U截面的压力与突扩接头前横截面积较小的出口处压力相等，代入式(39)，整理得到突扩接头油水两相分层流动的通用压降方程。

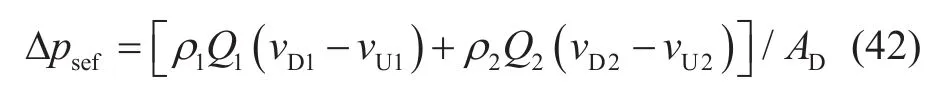
1.5 流体通过突缩接头的流动

突缩接头油水两相流动的控制体如图5所示。忽略摩擦应力和重力，并且假设上下两层不发生质量交换。

当流体从U-U截面流入，从最小收缩断面C-C截面流出时，流体加速，压力能转化为动能，在此过程中，只有少部分甚至没有摩擦耗散。而当流体流过收缩断面C-C截面后，流体的流动状态和突扩接头内流动状态相似，且伴有摩擦耗散的产生。基于均相流模型可建立突缩接头油水两相分散流动的通用压降方程，如式(43)所示。

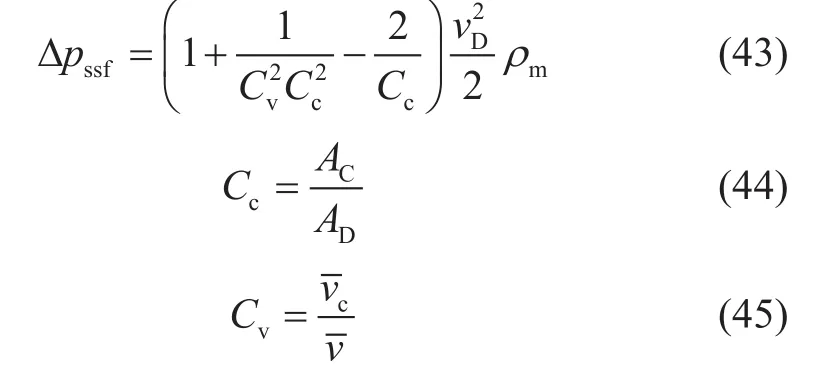
其中，Cc为收缩系数，无量纲；Cv为速度系数，无量纲；为流体在收缩断面的实际平均流速，m/s；为流体在收缩断面的理想平均流速，m/s。根据Oertel等人[20]的研究，对于AU=4AD的情况，Cc取0.637，Cv取 0.985。

基于双流体模型可列出突缩接头油水两相分层流动的动量方程。

其中，

相似地，C-C截面的压力与突缩接头前面横截面积较大的出口处压力相等，代入式(46)，并整理得到突缩接头油水两相分层流动的通用压降方程。

1.6 管路串并联理论

当直管和各种管件串联在一起时，有两个重要规律：

而当它们并联在一起时，这两个规律发生变化：

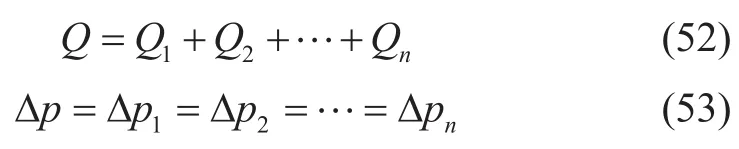
通过联立式(50)～(53)可求得复杂管路中油水两相流动的分流情况和压降。

1.7 模型闭合与求解

为了进一步区分4种分层流流型，还需引入一个附加条件。本文利用最小能值法概念[21]，认为系统能量最小时最稳定，对模型进行数值求解。该模型的求解流程如图6所示。首先，输入复杂管路的结构参数、流体性质和流量大小，对通道1的流量赋初值，并根据管路串并联理论计算通道2的流量。其次，判断流体在各通道中的流型，若为分散流，则计算混合液的性质，并根据均相流模型计算分流情况和压降。若为分层流，首先对上层含水率赋初值，并计算下层润湿周所对应的圆心角，根据双流体模型计算分流情况和压降。第三，判断两个通道的压降是否相等。若相等，输出流体参数并计算系统总势能；若不相等，更新通道1的流量。最后，迭代上层的含水率直至系统总势能最小，输出各通道的流型、流量和压降。

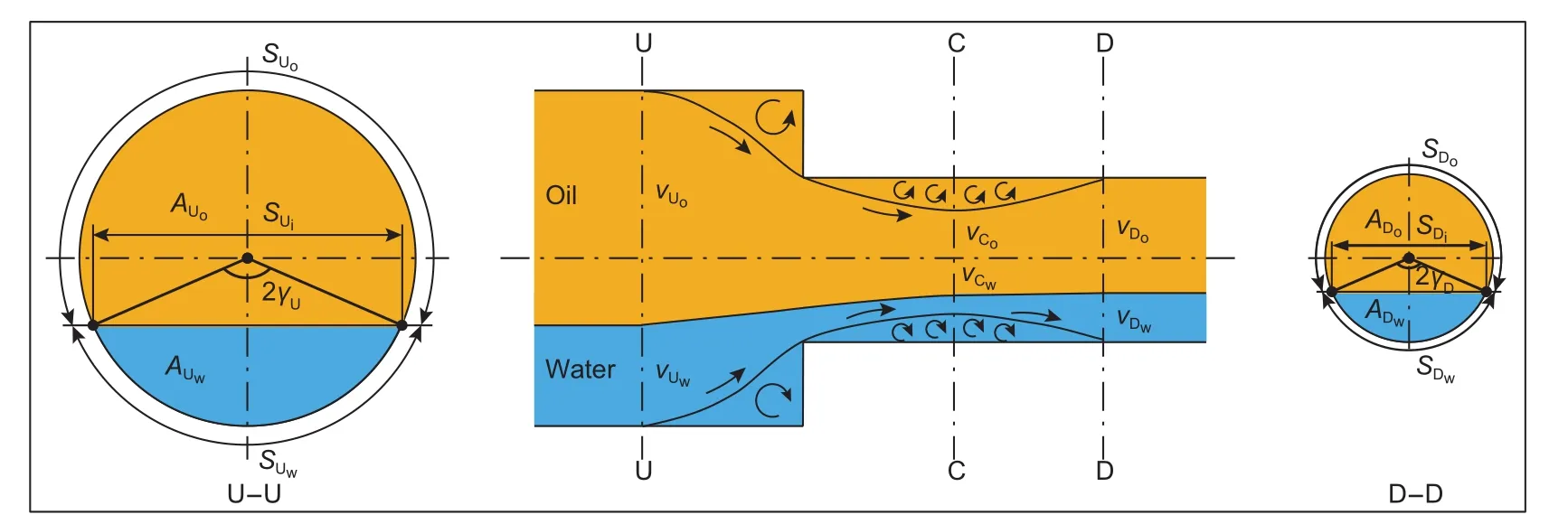
图5 突缩接头油水两相流动控制体示意图Fig. 5 Control volume of oil-water two-phase fl ow in the sudden shrunken fi tting

2 案例研究

图7为复杂管路的示意图，管路包含2个并联通道，各通道均由各种管道和管件串联而成，该实例包含了石油行业中常见的管件及连接方式。利用该实例对本文模型进行了验证，并与数值模拟结果进行了比较。

复杂管路的结构参数如表1所示，这些参数是在专业CAD软件SOLIDWORKS中生成的，通过CAD接口调入到FLUENT的前处理软件GAMBIT中，再通过布尔运算得到其内部流动模型并进行网格划分，计算单元总数约为300万。用FLUENT软件计算时，入口设为速度入口(Velocity-inlet)条件，出口设为出流(Out fl ow)条件，其他默认为壁面(Wall)条件。根据流体运动状态，分别采用层流模型和标准κ-ε模型模拟层流和湍流。而针对油水两相分散和分层流动，分别采用混合模型和VOF模型进行模拟。并设置入口流量为30 m3/d，可分别得到油相和水相通过复杂管路的速度流线图，如图8所示。

根据图8可以看出，油相和水相通过复杂管路后，分流情况差别很大，这是因为该实例中两并联管路的压降构成不同。通道1主要为局部摩阻，对水相阻力较大；通道2主要为沿程摩阻，其对油相阻力较大。油水混合物在不同油相黏度和含水率条件下，性质差别很大。为了准确描述含水率和油相黏度对分流情况和压降的影响，本文还研究了不同含水率和油相黏度条件下，油水两相流的分流情况和压降。含水率(%)取值如下：0、10、20、30、40、50、60、70、80、90、100；油相黏度(cP)取值如下：1、10、100，其他参数见表2。

将上述参数分别代入本模型和数值模拟中，求得油水两相通过复杂管路的分流情况和压降，如图9和图10所示。

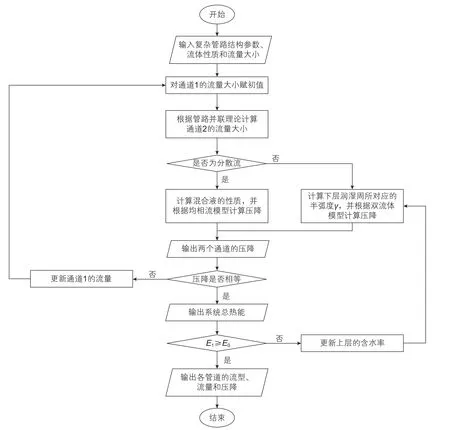
图6 复杂管路油/水两相流动的统一机理模型的求解流程图Fig. 6 Solving procedure for oil/water two-phase uni fi ed model in complex pipeline

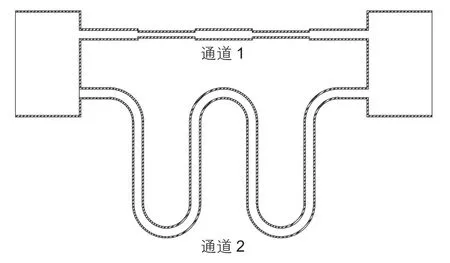
图7 复杂管路示意图Fig. 7 Diagram of the complex pipeline

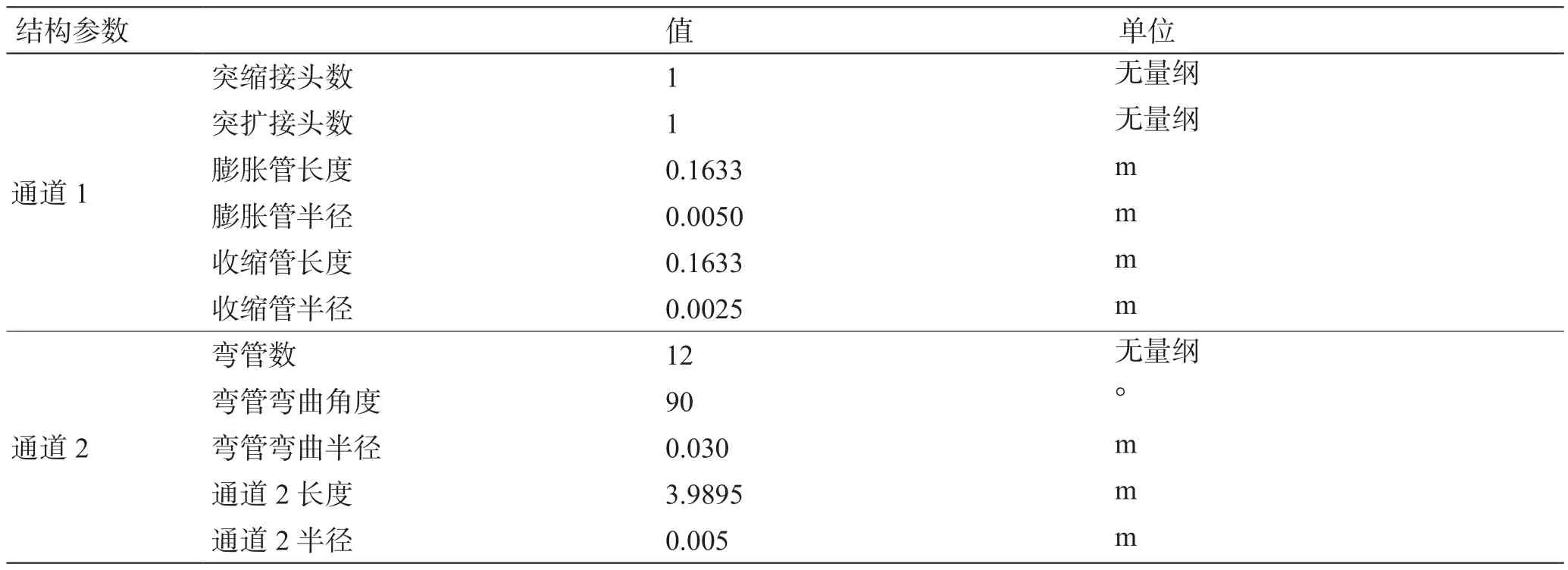
表1 复杂管路的结构参数Table 1 Structure parameters for the present complex pipeline

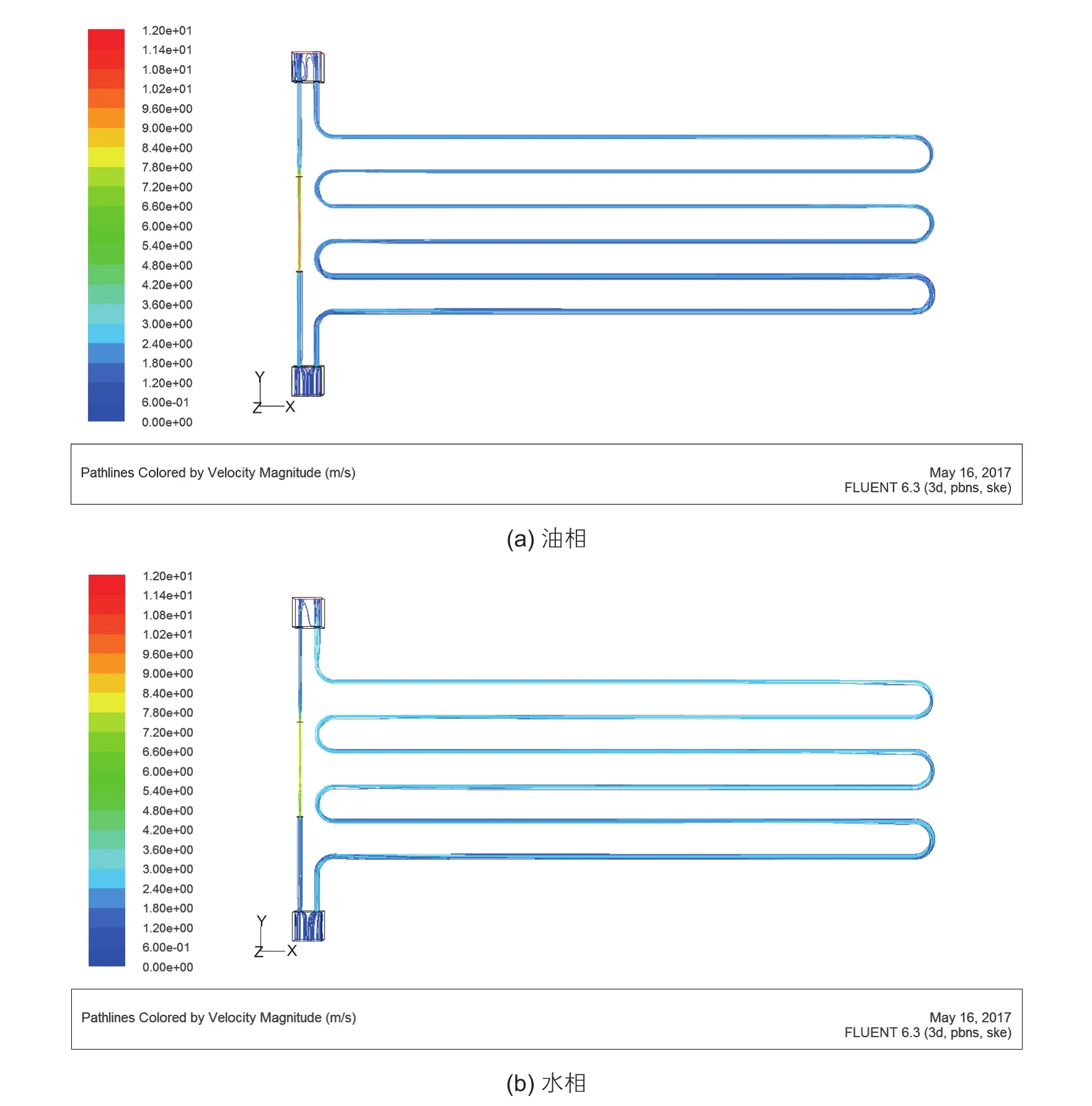
图8 速度流线图Fig. 8 Flow line colored by velocity magnitude

表2 复杂管路油水两相流动的流体参数Table 2 Fluid parameters for oil-water two-phase fl ow in the complex pipeline

图9 不同性质流体通过复杂管路的分流情况Fig. 9 Flow distribution through the complex pipeline with varying fl uid properties

图10 不同性质流体通过复杂管路所产生的压降Fig. 10 Pressure drop through the complex pipeline with varying fl uid properties

根据图9和图10可知，本文模型和数值模拟结果吻合良好，在体积含水率为0%～100%的条件下，绝对平均偏差最高为14.4%，总体平均偏差为9.8%。这些曲线都有3个主要的转折点：第1个为反相点，油相黏度越大，临界体积含水率越小，则反相点的位置越靠前；第2和3个点分别为流体从层流区过渡到湍流过渡区和从湍流过渡区过渡到湍流区的转折点。此外，如果混合液流速大于某一临界值时，流型也会发生转变，从而影响分流情况。

若混合液含水率大于临界含水率，由于此时水相占主导，油相黏度对分流情况和压降几乎没影响，所以油水两相流的分流情况和压降基本一致。当油相占主导时，不同油相黏度下，两相流分流情况和压降差别很大。且分流效果随油相黏度的增大而变好；随含水率的增加先变好后变坏，在临界含水率处最优。与之对应，油水两相流的压降随油相黏度的增大而变大；随含水率的增加先变大后变小，在临界含水率处最大。