基于正交试验设计的压裂管线冲蚀磨损参数效应分析
2019-01-02胡瑾秋李思洋张来斌
胡瑾秋,李思洋,张来斌
1 中国石油大学(北京)安全与海洋工程学院,北京 102249
2 中国石油大学(北京)油气资源与探测国家重点实验室,北京 102249
0 引言
随着页岩气勘探与开发技术地不断发展,以克服页岩储层低孔特征和低基质渗透率等缺陷[1]、提高油气产量为目的的大规模水力压裂技术的工艺、人员及设备安全日益受到人们的关注。就设备而言,水力压裂过程中的冲蚀磨损是引起材料破坏、设备失效的重要原因之一[2]。支撑剂颗粒在高速压裂液的携载下以切削、撞击、挤压等形式反复作用于固体管壁,极易导致管材刺漏、破裂,设备损坏等严重后果[3]。对此,众多学者基于实验及数值仿真模拟等方法对压裂过程中管道冲蚀磨损的作用机理、影响因素、预防措施等展开研究。
文献[4]探究了不同射流冲击角对冲蚀速率的影响。文献[5]通过对比数值模拟与失效分析的结果证实了基于粒子小角度切削及大角度碰撞引发塑性变形的冲蚀磨损机制。文献[6]分析了支撑剂浓度、携砂液流速、流体动力黏度、支撑剂粒径等参数对冲蚀结果的影响。在此基础上,文献[7]基于管道的应力状态提出了新的冲蚀磨损计算模型。文献[8]则通过分析质量载荷对冲蚀结果的影响解释了高颗粒浓度下冲蚀穿透率的衰减效应。文献[9]讨论了多相流入口流量和管径对弯管冲蚀和位移的影响。文献[10]基于数值模拟的结果分析了高压汇管液固两相流及支撑剂粒子的流动状态,从机理层面解释了管内压力、速度、冲蚀磨损等参数的分布状态及其对冲蚀结果造成的影响。文献[11]探究了冲蚀介质对冲蚀结果的影响。文献[12]针对八通注入头部件探究了压裂液流速差与冲蚀速率的关系。此外,针对直角弯管[13]、双弯头弯管[14]、连续管[15-16]、多种连接方式弯管[17]等对冲蚀磨损效应的影响研究也取得了一定成果。综上所述,目前压裂管线抗冲蚀磨损方面的理论研究多是讨论特定因素对冲蚀结果的影响(包括单一参数对冲蚀磨损结果的影响以及基于控制变量法的多参数作用对冲蚀磨损结果的影响)。其中“多参数作用对冲蚀磨损结果的影响研究”缺乏各参数间作用效果的横向比较,未讨论各参数对冲蚀磨损结果的影响力大小。
有鉴于此,本文采用基于正交试验设计的方法研究多种因素与管线冲蚀磨损结果之间的显著性关系,对比得出各因素对冲蚀磨损结果的影响力排序,为工程管线抗冲蚀磨损方案设计中各控制因素、操作步骤的优先级设置提供依据。
1 正交试验设计
正交试验设计(Orthogonal Design)是由日本质量管理专家田口玄一博士在多因素试验设计方法基础上提出的一种优化试验设计技术[18],旨在基于正交表的优越特性(正交性、代表性、综合可比性)通过较少次数的多因素试验取得较为准确、可靠的优选结论。
对于常规的单输入单输出系统,作为输入的初始状态、特征等,在一些因素的影响下会产生不同的响应输出。人们关注于不同因素及某一因素在不同水平对系统响应输出的影响,最直接的方法是进行多因素全面试验,即穷举所有对试验结果可能有影响的原因或要素(试验因素)及其变化的状态和条件(因素水平)分别进行试验以获取与响应输出对应的试验结果特性值(试验指标)。多因素全面试验能够完整覆盖与所选系统相关的全部因素水平,结果准确可靠、原理简单易懂,但试验次数随考察因素水平数的增加呈爆炸性增长,运算成本太高且效率低下。
正交试验设计基于均衡分布的思想,按照科学的构造准则从全面试验水平组合中挑选具有代表性的部分组合进行试验,既保证分析结果的准确性,又能大幅缩减试验次数,提高分析效率,是一种应用性极强的多因素系统分析处理的工具。其工作原理为:针对m因素n水平的试验对象(待考察试验指标有m个影响因素,每个因素有n个水平,全面试验共需nm次试验)建立正交表Lq(nm),其中L表示正交表,q表示水平组合数,即该试验基于正交试验设计需进行的试验次数,或称正交表行数;n为各因素的水平数,即某列不同信息的个数;m为因素数,即正交表的列数。根据生成正交表Lq(nm)的q个水平组合进行q次试验,分别得到q组对应的试验指标,再由正交试验结果分析确定优化水平组合,为进一步试验明确目标和方向。其中,基于均值主效应分析的计算方法如式(1)所示。
其中,x——试验指标代号,不同试验指标用不同字母表示;
m——因素序号;
n——第m个因素包含的水平序号;
——第m个因素对应的试验指标均值主效应值;
xim——第m个因素第i个水平对应的试验指标值。
正交试验方差分析计算方法如(2)~式(7)所示。

其中,SST,SSi,SSe——总平方和、各因素项平方和、误差平方和;
x——各水平组合对应试验指标值;
T——各水平组合对应试验指标之和;
n——水平组合数;
Ti——第i个因素项各水平对应试验指标之和;
ki——第i个因素项水平数;
dfT,dfi,dfe—— 总体自由度、各因素项自由度、误差自由度;
m——第i个因素项各水平重复数;
F——F检验值。
2 试验因素及试验指标选取
鉴于管道弯头部分冲蚀磨损比直管段严重约50倍[19],描述弯管形态的参数可作为试验因素,本文以“管径”[20]和“弯头圆角半径”因素为例;除管道形态外,描述流体性质的参数也应作为试验因素,本文选取“介质入口流速”和“支撑剂粒径”[21]因素为例。因此,本文研究的试验因素组合为:(1)管径;(2)弯头圆角半径;(3)介质入口流速;(4)支撑剂粒径。
就液体介质对管道的冲蚀效果而言,液体介质的速度场变化、对管壁的压力场变化以及管壁最大冲蚀率可作为管壁冲蚀磨损程度的评价指标[22]。则本文选取“径向流速”、“切向流速”、“管壁总压力”、“管壁最大冲蚀率”作为试验指标,衡量管线冲蚀磨损程度。
其中,径向流速表征液体介质经过弯头处时受离心力作用沿垂直于管壁方向的转移能力,数值越小,液体介质中支撑剂颗粒向管壁方向的冲击能力越弱,冲蚀效果越弱。
切向流速表征液体介质经过弯头处后受离心力作用沿平行于管壁方向的转移能力,数值越大,液体介质中支撑剂颗粒向管壁方向的冲击能力越弱,冲蚀效果越弱。
管壁总压力表征液体介质对管壁的垂向作用,数值越大,冲蚀效果越强。
管壁最大冲蚀率即管材单位时间、单位面积受冲蚀作用损失的材料质量,数值越大,冲蚀效果越强。
3 分析步骤
结合前文选定的试验因素、试验指标及正交试验设计的基本原理,本文分析步骤如下:
【步骤1】选定管道冲蚀磨损过程待考察的试验指标,即径向流速(m/s)、切向流速(m/s)、管壁总压力(Pa)、壁面最大冲蚀率(kg/(m2·s))。选定管道冲蚀磨损过程中影响试验指标的试验因素为:管径(mm)、圆角半径(mm)、支撑剂粒径(mm)、入口流速(m/s)。
【步骤2】设定各试验因素的水平,并基于设定因素、水平设计正交试验表。
【步骤3】根据正交试验表各行的因素水平安排试验方案,建立不同管径及圆角半径的钢管模型,调整冲蚀模型中的离散相粒径及入口流速对应于支撑剂粒径因素及入口流速因素的各水平数值,应用Fluent软件仿真模拟求出各实验条件下的试验指标值填入正交表中。
【步骤4】对正交试验结果进行均值主效应分析(如式1)及方差分析,确定管径、圆角半径、支撑剂粒径、入口流速等因素对各试验指标影响的显著程度并排序。
4 案例分析
针对选定的试验因素“管径”、“弯头圆角半径”、“介质入口流速”、“支撑剂粒径”,案例分析中设定其因素水平如表1所示。
则研究对象为四因素四水平,总试验次数应为44=256次。为缩减仿真试验次数,提高分析效率,可采取正交试验的设计方法建立正交表,按正交试验原理则只需进行16次仿真试验。压裂管线冲蚀磨损参数效应分析正交试验表(含试验指标值)如表2所示。

表1 案例分析试验因素及因素水平Table 1 Test factors and levels of factors in the case analysis
4.1 均值主效应分析
根据表2做正交试验分析。以径向流速为响应数据时,均值主效应如图1(a)所示。均值主效应表如表3(a)所示。以切向流速、管壁总压力、管壁最大冲蚀率为响应数据时均值主效应图及表分别如图1(b)~1(d)及表 3(b)~3(d)所示
由表3“排序”结果可知,选取不同试验指标作研究对象时,各因素对试验指标的效应优先级排序有所不同。即:
(1)以径向流速作为试验指标来衡量管线冲蚀磨损严重度时,入口流速因素的影响最大(排序1),且当入口流速因素选择水平1(10 m/s)时,径向流速最小,即冲蚀效果最弱。弯角半径因素影响排第二(排序2),
且当弯角半径因素选择水平1(60 mm)时,径向流速最小,冲蚀效果最弱。同理,管径因素影响排第三(排序3),当其选择水平2(45 mm)时,冲蚀效果最弱。支撑剂粒径因素影响排第四(排序4),且当其选择水平1(0.10mm)时,冲蚀效果最弱。

表2 冲蚀磨损多参数效应分析正交试验表Table 2 Orthogonal test table of effect analysis of multiple parameters on erosion wear
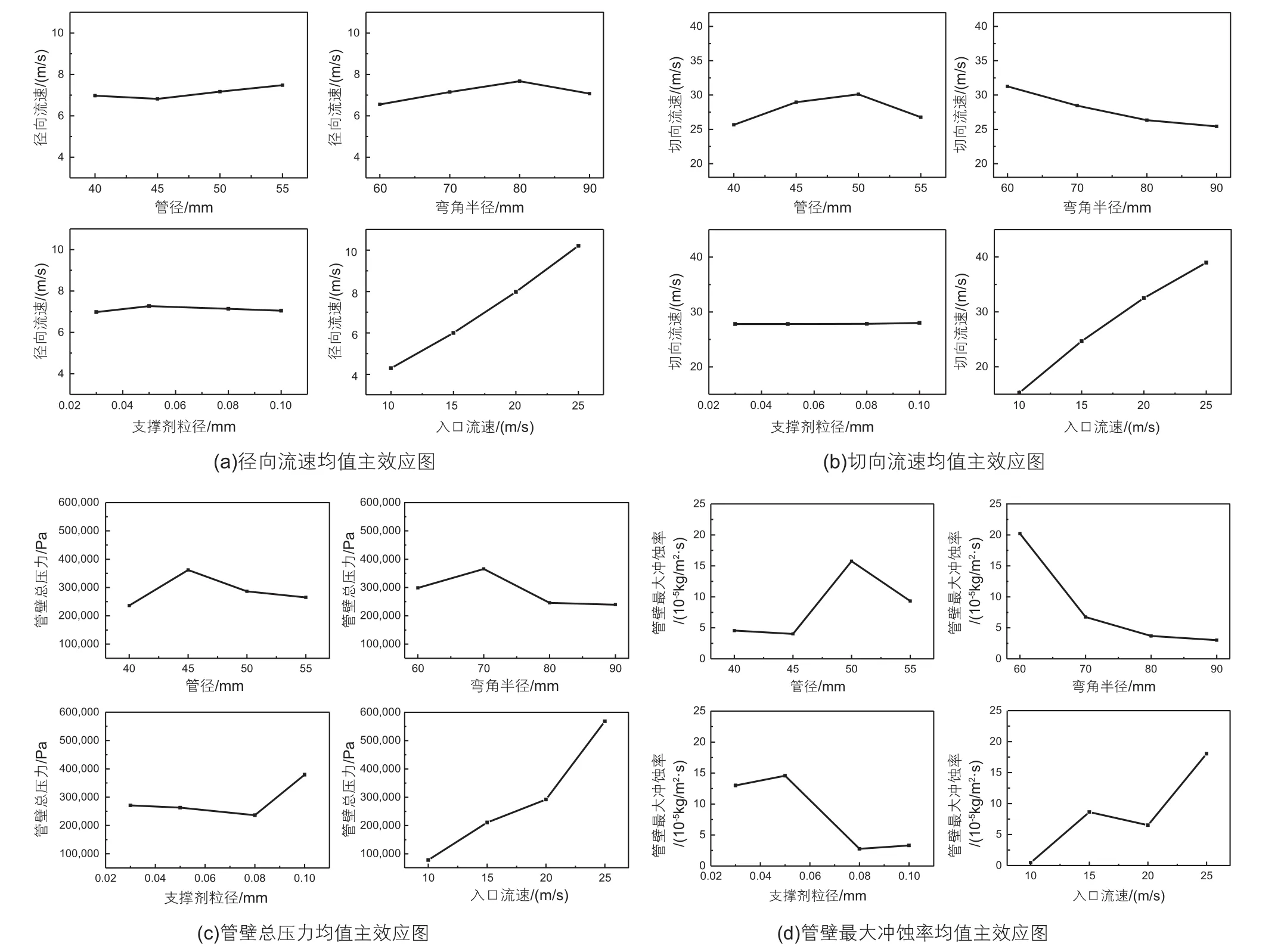
图1 正交试验分析均值主效应图Fig. 1 The mean main effect map of orthogonal test analysis

表3 正交试验分析均值主效应表Table 3 The mean main effect table of orthogonal test analysis
(2)以切向流速作为试验指标来衡量管线冲蚀磨损严重度时,入口流速因素的影响最大(排序1),当选择水平4(25 m/s)时,切向流速最大,冲蚀效果最弱。弯角半径因素影响排第二(排序2),且当弯角半径因素选择水平1(60 mm)时,切向流速最大,即冲蚀效果最弱。管径因素影响排第三(排序3),且当其选择水平3(55mm)时,冲蚀效果最弱。支撑剂粒径因素影响排第四(排序4),当其选择水平4(0.03 mm)时,冲蚀效果最弱。
(3)以管壁总压力作为试验指标来衡量管线冲蚀磨损严重度时,入口流速因素的影响最大(排序1),且当选择水平1(10 m/s)时,管壁总压力最小,冲蚀效果最弱。支撑剂粒径因素影响排第二(排序2),当选择水平3(0.05 mm)时,冲蚀效果最弱。弯角半径因素影响排第三(排序3),选择水平4(90 mm)时,冲蚀效果最弱。管径因素影响排第四(排序4),且当其选择水平1(40 mm)时,冲蚀效果最弱。
(4)以管壁最大冲蚀率作为试验指标衡量管线冲蚀磨损严重度时,入口流速因素的影响最大(排序1),且当入口流速因素选择水平1(10 m/s)时,管壁最大冲蚀率最小,即冲蚀效果最弱;弯角半径因素影响第二(排序2),且当弯角半径因素选择水平4(90 mm)时,冲蚀效果最弱;支撑剂粒径因素影响第三(排序3),且当其选择水平3(0.05 mm)时冲蚀效果最弱;管径因素影响第四(排序4),且当其选择水平2(45 mm)时,冲蚀效果最弱。
4.2 方差分析
对径向流速、切向流速、管壁总压力、管壁最大冲蚀率四项指标作方差分析见表4~表7所示。其中,F、P为F检验的临界值及概率值;S为回归模型偏差的标准方差。R-Sq为回归模型偏差占总偏差的百分比,取值在0和1之间,数值越接近于1,表明回归模型与数据吻合得越好。R-Sq(Adj)即调整R-Sq,取值在0和1之间,R-Sq(Adj)与R-Sq越接近,表明回归模型越可靠。
(1)针对径向流速的方差分析结果如表4所示,入口流速F值85.43最大,显著性水平P=0.002,<0.05,即在95%的置信水平上,说明入口流速因素与径向流速指标存在显著性相关。该模型中R-Sq=98.89%,表明回归模型与数据拟合良好,R-Sq(Adj)=94.47%与98.89%较为接近,表明回归模型可靠性高。则以径向流速为考察指标来评价冲蚀磨损程度时,入口流速因素的影响效应最大。
(2)针对切向流速的方差分析结果如表5所示,入口流速F值173.23最大,且显著性水平P=0.001,<0.05,即在95%的置信水平上,入口流速因素与切向流速指标存在显著性相关。模型中R-Sq=99.48%,表明回归模型与数据拟合良好,R-Sq(Adj)=97.40%与99.48%较为接近,表明回归模型可靠性高。以切向流速为考察指标来评价冲蚀磨损程度时,入口流速因素的影响效应最大。
(3)针对管壁总压力的方差分析结果如表6所示,入口流速F值7.97最大,显著性水平0.05<P<0.1,即在90%的置信水平上,入口流速因素与管壁总压力指标存在显著性相关。该模型中R-Sq=90.81%,表明回归模型与数据拟合较好,但R-Sq(Adj)=54.07%与90.81%相差较大,表明回归模型可靠性低。以管壁总压力为考察指标评价冲蚀磨损程度时,入口流速因素的影响效应最大,但结果可信度比“径向流速”和“切向流速”分析低。

表4 径向流速方差分析Table 4 Variance analysis of radial fl ow velocity

表5 切向流速方差分析Table 5 Variance analysis of axial fl ow velocity
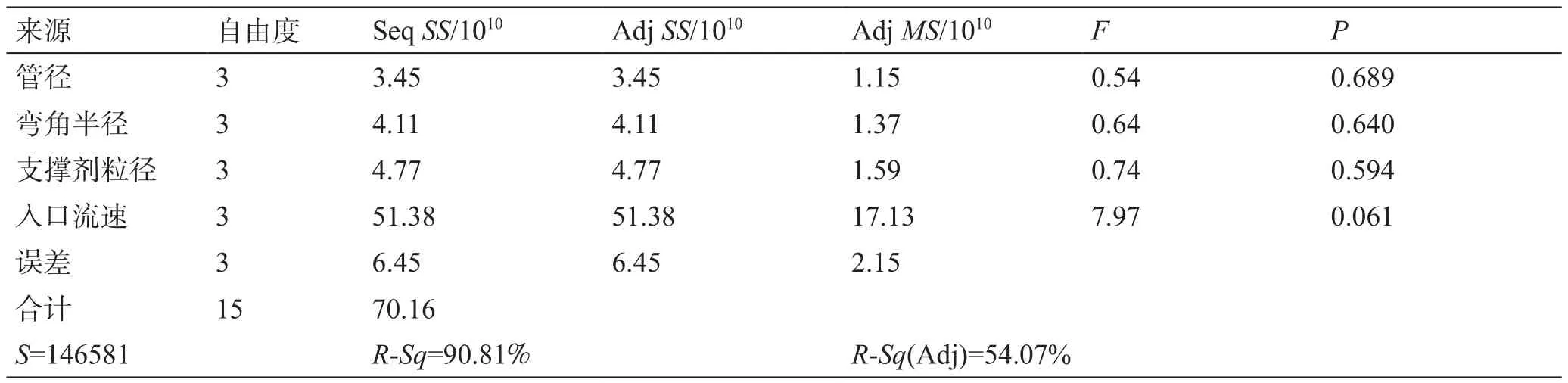
表6 管壁总压力方差分析Table 6 Variance analysis of total pressure on the wall
(4)针对管壁最大冲蚀率的方差分析结果如表7所示,弯角半径F值2.99最大,显著性水平0.1<P<0.2,即在80%的置信水平上,弯角半径与管壁最大冲蚀率指标存在显著性相关。此外,入口流速F值为2.47,显著性水平0.2<P<0.25,说明在75%的置信水平上,入口流速与管壁最大冲蚀率指标存在显著性相关。该模型中R-Sq=89.63%,表明回归模型与数据拟合较好,但R-Sq(Adj)=48.14%与89.63%相差较大,表明回归模型可靠性低。
综上所述,以管壁最大冲蚀率为考察指标评价冲蚀磨损程度时,弯角半径因素的影响效应最大,但与入口流速因素的影响效应相差不大,且结果可信度相比“径向流速”和“切向流速”分析而言较低。
针对四项试验指标的方差分析结果评价如表8所示。分析可知,入口流速因素与四项试验指标都存在显著性相关,即入口流速因素对冲蚀磨损严重程度的效应最明显;弯头圆角半径与四项试验指标存在一定程度的相关,但相关性小于入口流速因素;支撑剂粒径与四项试验指标不存在显著性相关,说明其对冲蚀磨损程度的效应相比其它三个因素最弱。
5 结论
(1) 本文针对压裂管线的冲蚀磨损问题,基于正交试验设计方法,研究了管径、弯头圆角半径、支撑剂粒径、入口流速等因素与管线冲蚀磨损严重度之间的显著性关系。比较了各因素对冲蚀磨损结果的影响力排序,为工程管线抗冲蚀磨损方案设计中各控制因素、操作步骤的优先级设置提供依据。
(2) 由主效应分析可知,入口流速对径向流速、切向流速、管壁总压力、管壁最大冲蚀磨损率等指标的影响最大(对四项试验指标的主效应优先级排序分别为1、1、1、1),弯角半径影响其次(对四项试验指标的主效应优先级排序分别为2、2、3、2),支撑剂粒径和管径影响较小。
(3) 由方差分析结果可知,入口流速因素与四项试验指标都存在显著性相关(最大置信度95%,最小置信度75%),即入口流速因素对冲蚀磨损严重程度的效应最明显;弯头圆角半径与三项试验指标存在一定程度的相关性(最大置信度95%,最小置信度75%),但相关性弱于入口流速因素;支撑剂粒径与四项试验指标不存在显著性相关,说明其对冲蚀磨损程度的效应相比其它三个因素最弱。
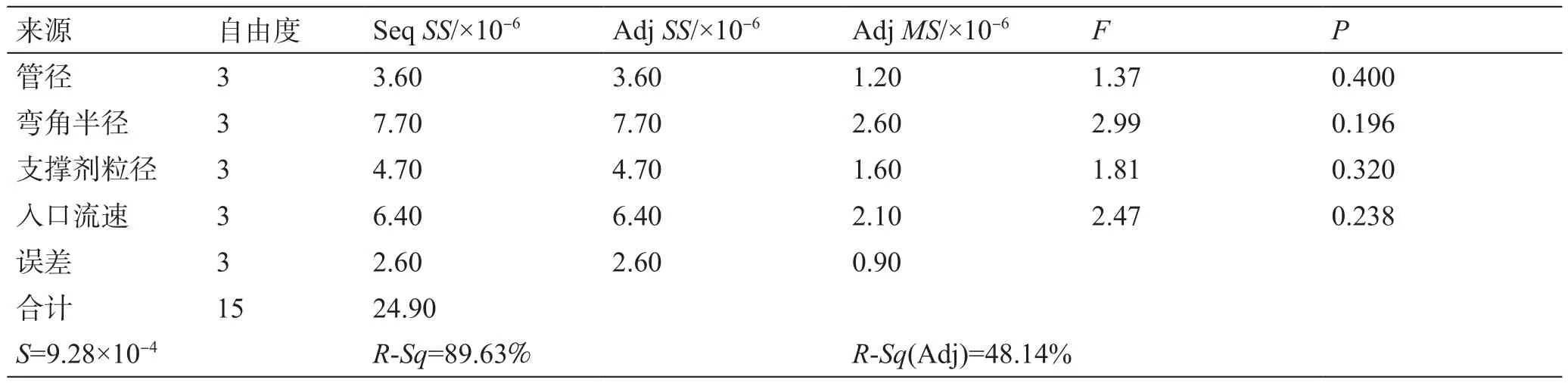
表7 管壁最大冲蚀率方差分析Table 7 Variance analysis of the maximum erosion rate of pipe wall
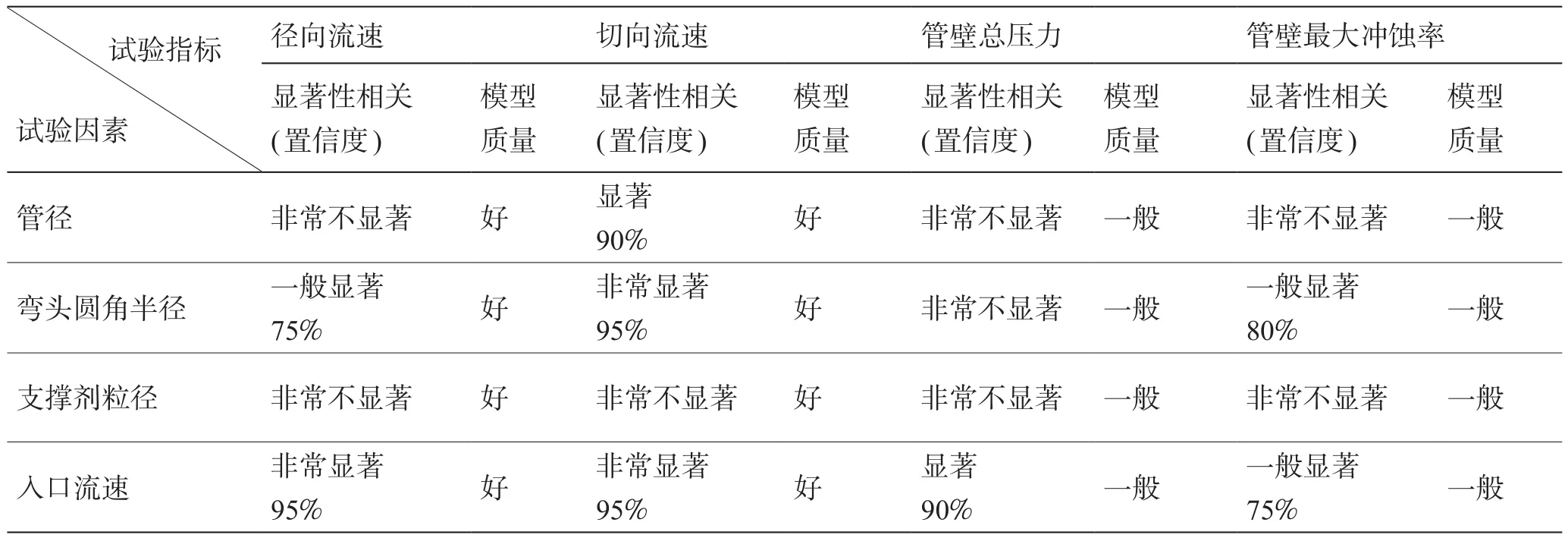
表8 试验指标方差分析结果评价Table 8 Evaluation of variance analysis results of test indexes
