双重有效应力再认识及其综合作用

毛小龙，刘月田，冯月丽，郑文宽，刘思平

中国石油大学油气资源与探测国家重点实验室，北京 102249

0 引言

Terzaghi[1-3]有效应力原理是土力学的奠基石，是土力学成为一门独立学科的重要标志。Terzaghi有效应力原理是基于实验观察结果提出的，实验中多孔介质(如砂土、黏土和混凝土)在静水压中是似乎不可压缩的，其引起的土体体积和强度变化几乎观察不到；土体体积和强度变化仅仅由总应力与孔隙流压力的差值变化引起；定义孔隙流体压力为中和应力，有效应力为总应力与孔隙流压之差：

式中，σeff为有效应力，σ为总应力，p为孔隙流压，单位为Pa或者MPa。

Terzaghi实验测试压力为0到数百个大气压，假设土颗粒不可压缩(土颗粒压缩系数相对于土体压缩系数极小)，土体变形完全由颗粒间变形引起。基于Terzaghi有效应力原理不考虑颗粒变形，李传亮[4]于1999年提出了双重有效应力这一概念：定义因骨架颗粒的变形而导致的介质整体变形为本体变形，对应于本体有效应力；因介质骨架颗粒空间结构上的变化即骨架颗粒之间的相对位移而导致的介质整体变形为结构变形，对应于结构有效应力，多孔介质总变形是这两种变形的代数和。本体有效应力和结构有效应力分别为：

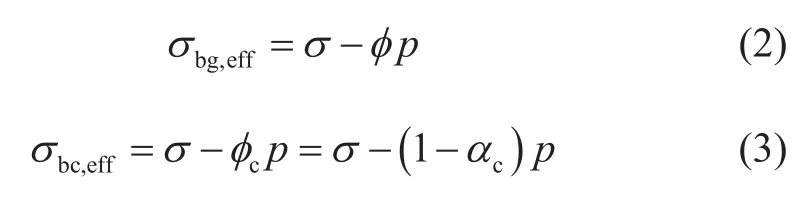
式中，σbg,eff为本体有效应力，σbc,eff为结构有效应力，单位为Pa或者MPa；φ为孔隙度，φc接触孔隙度，αc为颗粒间接触面积与总横截面积的比值。

双重有效应力概念的提出为多孔介质力学的发展起到了一定的推动作用。双重有效应力本体变形和结构变形与国外许多学者50～60年代提出的颗粒变形和颗粒间变形内涵相同，而油藏工程中，由于有双重介质这一相近名词，使得双重有效应力这个概念简洁易懂，被国内许多油藏工程学者引用。据中国知网统计，截至2018年5月，提出双重有效应力的文献[4]直接引用量已达到189次，基于双重有效应力的压缩系数和应力敏感等各种相关研究则更为广泛。然而，两个有效应力表达式与Biot[5-6]、Bishop[7]等学者早期提出的两个有效应力表达式相同，而这两个表达式与1955年Laughton[8]经典铅粒高压实验相矛盾，在60年代后被逐渐弃用，Skempton[9]、Biship[10]等人提出的有效应力表达式则渐渐被接受。此外，由李传亮双重有效应力原理导出的相关理论体系出现了许多与实验相矛盾的认识。首先，其认为岩石孔隙压缩系数比岩石颗粒压缩系数低，其值应该在10-7～10-5MPa-1级别，而不是实验测试得到的10-4～10-3MPa-1级别[11]；同时，认为岩石孔隙压缩系数应该与孔隙度成正比，即认为传统实验测试和Hall[12]图版存在逻辑反转问题[13-14]；而且还认为低渗透储集层应力敏感比高渗透储层应力敏感更低，而不是低渗透储层应力敏感更强[15]。这些认识引发了极大的争议[16-19]，给油藏工程研究造成了困扰，因此十分有必要重新推导双重有效应力的正确表达式，从而方便其在油藏工程中正确应用。

本文将在多孔介质应力应变分析基础上，推导出新的双重有效应力表达式，并分析其综合作用效果得到其总有效应力表达式，并与Laughton[8]等实验、Hall[12]图版结果对比，论证其正确性和适用性。

1 多孔介质应力应变分析

先分析颗粒应力和颗粒间应力：

(1)以穿过颗粒的宏观界面为受力对象，总应力为σ，受力面积为A，孔隙流压p，孔隙流体受力面积为φA，颗粒真实平均应力为σg，颗粒受力面积为(1-)φA。横截面上受力平衡有：

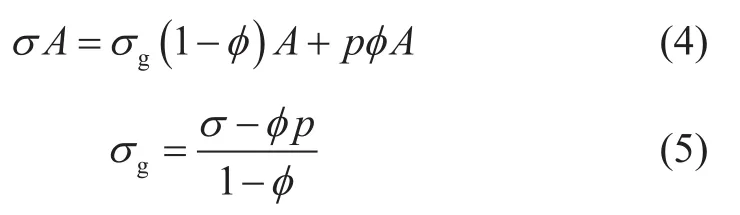
等效平均到整个介质横截面积之上，颗粒等效平均应力σs为：

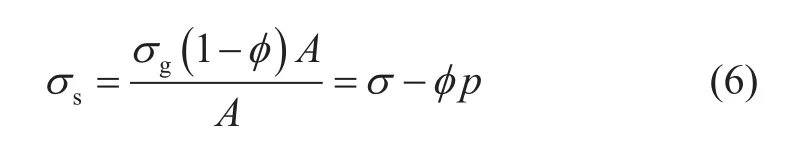
Biot[5-6]在1955年曾认为低渗多孔介质有效应力系数η=φ，方程(6)为有效应力方程，而李传亮[4]则将其看作本体有效应力方程,即本体有效应力等于颗粒等效平均应力σs。

(2)取颗粒间的接触界面作受力分析，总应力为σ，受力面积为A，颗粒间真实平均应力为σij，颗粒间接触面积为Aij=αcA，孔隙流体压力p，受力面积为(1-αc)A。

颗粒间接触面受力平衡有：

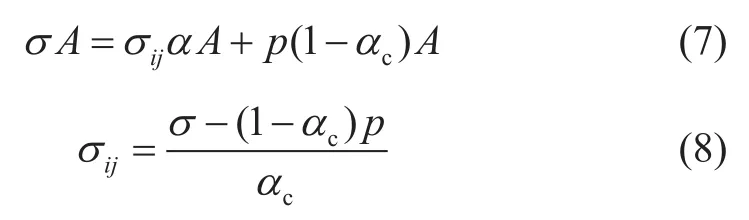
等效平均到整个介质横截面积之上，颗粒间等效平均应力σc为：

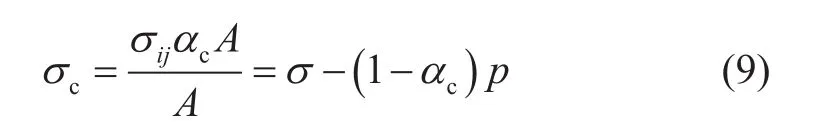
Bishop[7]1959年曾认为颗粒间等效平均应力σc为有效应力方程，而李传亮[4]则将其看作结构有效应力方程,即结构有效应力等于颗粒等效平均应力σc。

然而，颗粒等效平均应力和颗粒间等效平均应力是否为引起骨架本体变形和结构变形的有效应力呢？李广信[20]、邵龙潭[21]等学者详细分析了有效应力内涵，并指出这是一个常见的认识误区。实际上，颗粒等效平均应力并不能决定介质整体本体变形，颗粒间等效平均应力也不能决定骨架整体结构变形。以多孔介质浸没在静水压中为例，此时总应力和孔隙流压均为p，代入方程(5)和(8)，颗粒真实平均应力σg、颗粒间真实平均应力σg为：

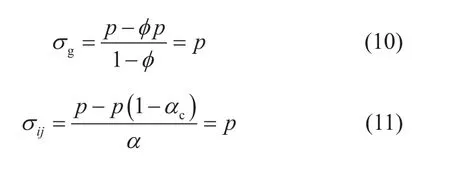
而对于完全浸没在静水压中的多孔介质，无论其微观颗粒间接触面积和孔隙度为多少，多孔介质各处所受应力均为p。其微观颗粒和宏观整体都在应力p下均匀压缩，本体有效应力应为p，无颗粒间变形或结构变形，结构有效应力应为0。而总应力和孔隙流压均为p时，代入方程(6)和方程(9)得到颗粒等效平均应力和颗粒间等效平均应力分别为：

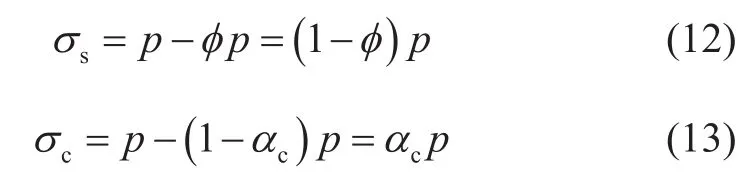
这与本体有效应力应为p、结构有效应力为0的实际情况不一致，颗粒等效平均应力、颗粒间等效平均应力大小均不能决定本体变形和结构变形大小，需要重新认识。此外，颗粒等效平均应力和颗粒间等效平均应力表达式分别与孔隙度、颗粒间接触面积有关，而1955年Laughton[8]经典铅粒高压实验表明：改变总应力和流压，无论颗粒接触面积为0.03、0.11还是0.95，孔隙度为0.4、0.31还是0.03，铅粒多孔介质有效应力系数均接近于1，其有效应力与孔隙度、接触面积均无直接关系，这也说明旧双重有效应力存在问题。

2 新双重有效应力及其综合作用

本文在研究新双重有效应力时仍分为本体有效有效力和结构有效应力，分别对应本体应变和结构应变，然后两个有效应力综合起来得到总有效应力和总应变。

2.1 新结构有效应力

从上文分析可知，在静水压中，颗粒均匀受力，颗粒间真实平均应力为p，但结构变形为0，这说明于颗粒间真实平均应力p并不会引起颗粒间变形。颗粒间作用力中至少有一部分用来平衡流压p，这部分应力与孔隙流压共同作用，均匀压缩颗粒从而不产生结构变形；只有平衡流压之外的净应力集中作用在颗粒接触面上产生额外的偏应力，从而引起颗粒间滑动变形，产生介质结构变形。即引起颗粒间变形的真正有效的应力为超出平衡孔隙流压之外的颗粒间应力，由方程(8)可得：

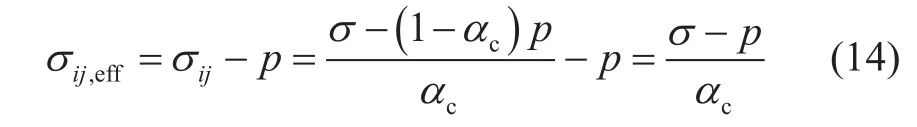
等效平均到整个介质横截面积之上，其对应的等效平均应力σc,eff即为结构有效应力：

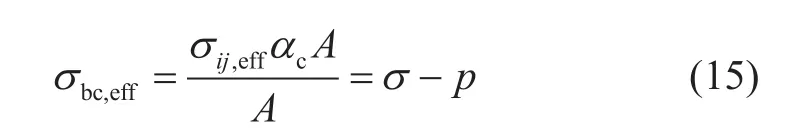
结构有效应力表达式与Terzaghi有效应力原理表达式完全一致, 这说明当颗粒变形可忽略时，Terzaghi有效应力即为结构有效应力，其物理意义为超出平衡孔隙流压之外的颗粒间等效平均应力，大小为总应力与孔隙流压的差值。定义结构变形(颗粒间变形)引起的介质整体体积结构压缩系数为Cbc，对应的介质整体体积结构应变为：

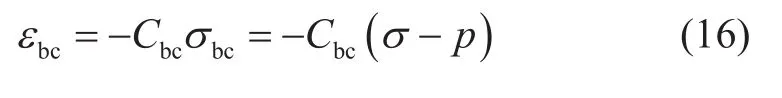
2.2 新本体有效应力

本体变形中为颗粒变形引起的介质整体变形，除了颗粒体积变形，本文新提出一种由颗粒形状变形引起的介质整体变形。颗粒体积变形和形状变形受力示意图如图1所示。

颗粒受到孔隙流压和颗粒间应力的共同作用。为方便计算，将颗粒间应力分为两部分来计算：一部分用来平衡孔隙流压p，与孔隙流压共同作用均匀压缩颗粒，只引起颗粒体积变形，不引起颗粒形状变形；另外一部分为超出平衡孔隙流压之外的颗粒间应力(σij-p)，这部分作用力集中作用在颗粒间接触面积上，不但引起颗粒体积变形，还引起颗粒形状变形。根据方程(5)、(14)，颗粒真实平均应力为这两部分之和：

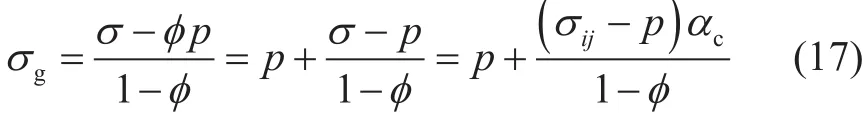
方程(17)中分为两部分作用力具有重要意义，两部分作用力效果不同：前部分p均匀压缩颗粒，只引起颗粒体积变形；后部分集中作用于颗粒间接触面，同时引起颗粒体积变形和颗粒形状变形。由接触力学可知，颗粒真实平均应力大小无法反应出颗粒不均匀受力(应力集中)而产生的形状变形，从而无法计算由颗粒形状变形引起的骨架整体应变，因此不能用颗粒真实平均应力作为本体有效应力。

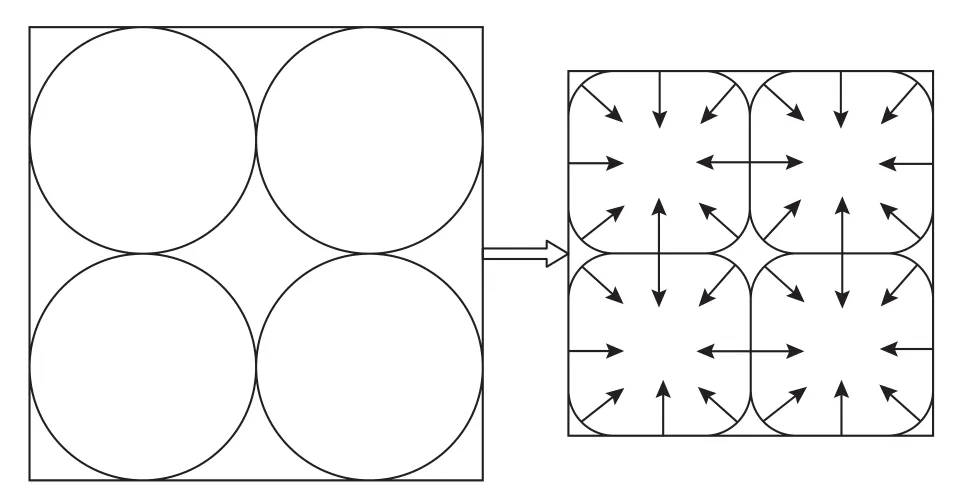
图1 颗粒体积变形和形状变形受力示意图Fig. 1 Stress schematic diagram of grain volume deformation and shape deformation

颗粒体积压缩系数Cs只能用于计算颗粒体积变形及其引起的多孔介质整体等比例变形，引起颗粒体积变形为孔隙流压和颗粒间集中应力两部分引起，根据方程(17),由颗粒体积变形引起的整体体积变形εbs为：

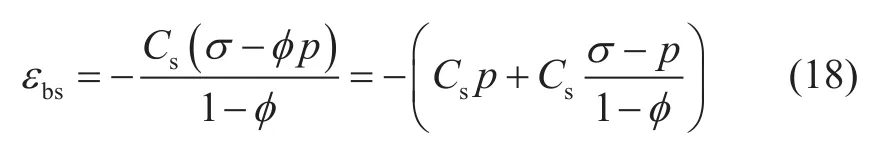
方程(18)与文献[13-14]中应变表达式一致。定义因颗粒形状变形引起的整体体积应变压缩系数为Cbsc，只有颗粒间集中应力(σij-p)会引起颗粒形状变形，颗粒形状变形引起的整体体积应变εbsc为：

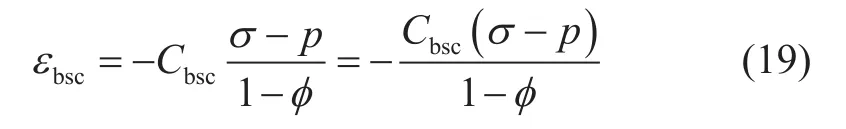
将方程(18)和(19)相加，颗粒体积变形和颗粒形状变形共同引起的整体本体应变εbg为：

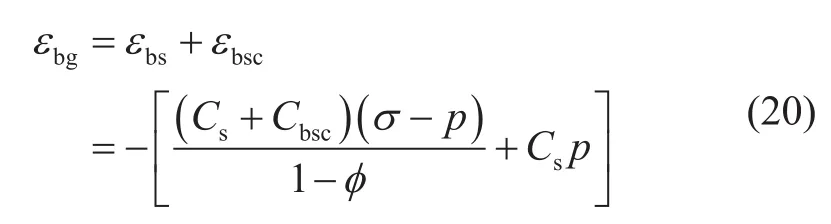
定义恒流压变总应力条件下，由颗粒体积变形和颗粒形状变形引起的整体应变压缩系数Cbg为：

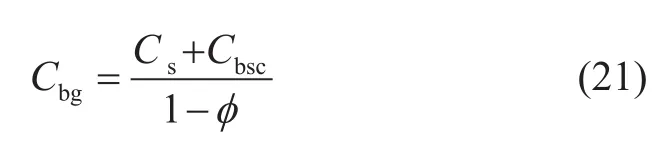
方程(21)代入方程(20)计算得到：

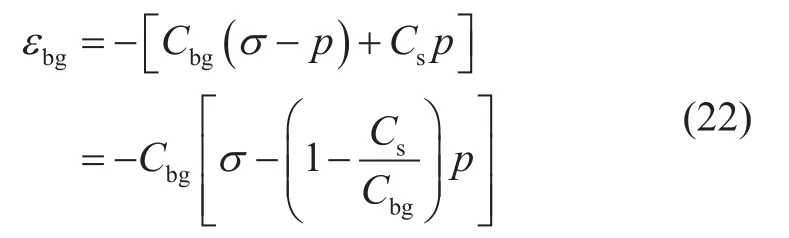
与颗粒变形(包括颗粒体积变形和颗粒形状变形)对应的本体有效应力σbg,eff为：

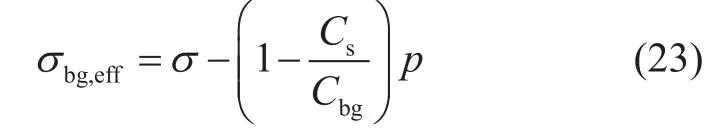
2.3 综合作用及总有效应力

从新双重有效应力方程可知，多孔介质变形由颗粒体积变形、颗粒形状变形和颗粒间变形引起，受均匀应力p和颗粒间集中应力(σij-p)两部分影响。其中均匀应力p只引起颗粒体积变形，颗粒间集中应力(σij-p)同时引起颗粒体积变形、颗粒形状变形和颗粒间变形。两个有效应力方程综合作用共同引起多孔介质总应变，本构有效应力和结构有效应力综合作用得到总应变，将方程(22)，(16)相加，介质整体体积总应变εb为：

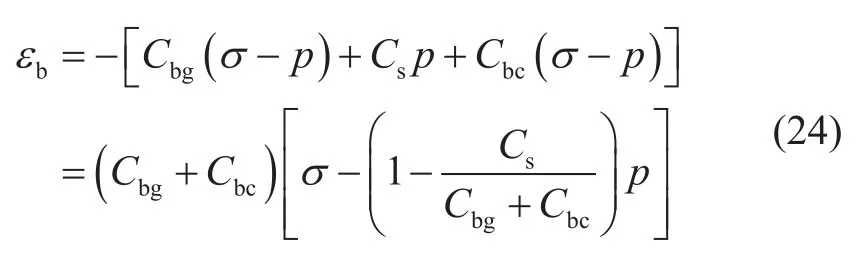
定义本体变形和结构变形引起的整体综合压缩系数C为：

方程(25)代入(24)得到：

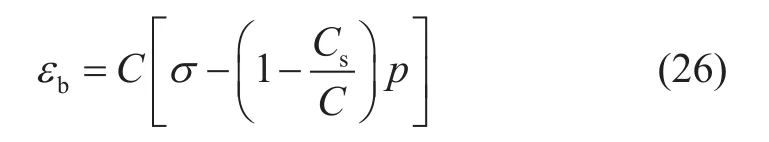
对应的总有效应力σb,eff为：

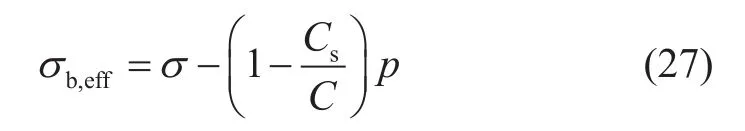
整体体积综合压缩系数C即为Skempton有效应力方程定义的骨架总体积在恒流压变总应力条件下的介质总压缩系数。两个新双重有效应力(本构有效应力和结构有效应力)综合作用得到的总有效应力表达式(27)与Skempton有效应力方程完全一致，此外，Biot& Willis (1957)[22]、Bishop(1973)[10]等学者从岩石地震声波传播和岩石体积模量关系等不同角度研究也得到了相同的有效应力表达式。

总之，利用新双重有效应力理论研究多孔介质应力应变机理时，可将其则分为颗粒变形(颗粒体积变形和颗粒形状变形)和颗粒间变形讨论和分析，在计算多孔总应变时，则可直接从多孔介质两部分作用力作用效果和两部分压缩系数出发直接计算：一部分为各处均匀压缩多孔介质颗粒的多孔介质净流压p，其压缩系数为Cs，只引起颗粒体积变形；超出平衡流压并作用在颗粒间接触面的等效平均应力(σ-p)，其压缩系数为C，同时引起颗粒体积变形、颗粒形状变形和颗粒间变形；两部分应力引起的应变直接相加即总应变，其对应的等效应力为总有效应力。

旧双重有效应力在研究岩石变形时认为其变形主要为颗粒体积变形，忽略了颗粒形状变形和颗粒间变形的影响，在多数情况下，会出现较大的计算误差，其得出的相关理论规律与实验结果相矛盾，而新计算出的公式则能很好的与实验结果相吻合，并能很好的应用到孔隙压缩系数及应力敏感研究中，下面两部分将对此进行详细阐述。

3 新理论解释实验测试结果

目前，实验测试很难直接精确测量得到颗粒变形、颗粒形状变形和颗粒间变形对应的压缩系数分量。在实验测试中常用的两种测试方法为夹持测试和不夹持测试，即将试样浸没在水中加流体压力、测试得到颗粒压缩系数Cs和恒流压变总应力测试综合压缩系数C的两种测试。虽然很难定义精确测试得到多孔介质三种变形的分量大小，但在不同条件下，颗粒变形、颗粒形状变形和颗粒间的变形相对大小则很容易分辨，可用于分析和解释经典实验中不同介质变形的主要变形机理和规律。

下面对一些经典实验结果进行解释分析。

(1)1955年Laughton经典铅粒高压实验

实验测试结果见表1。其为松散铅粒压实固结实验，铅颗粒泊松比0.44，极易形状变形，杨氏模量16.4 GPa，体积模量45.6 GPa，体积压缩系数为0.02 GPa-1，即使100 MPa高压下，其颗粒体积应变量也只有0.002。实验测试中随着有效应力不断增大，孔隙度大幅度减小，颗粒间接触面积在不断增大，有效应力系数却一直接近于1，这是因为铅粒多孔介质变形主要由颗粒形状变形和颗粒间变形引起，其有效应力为控制颗粒形状变形和颗粒间变形的净应力(σ-p)。没有颗粒形状变形机理，则无法解释孔隙度被压缩到接近于0的实验过程，用旧双重有效应力理论也无法解释有效应力系数在孔隙为0时依然接近1的测试结果。

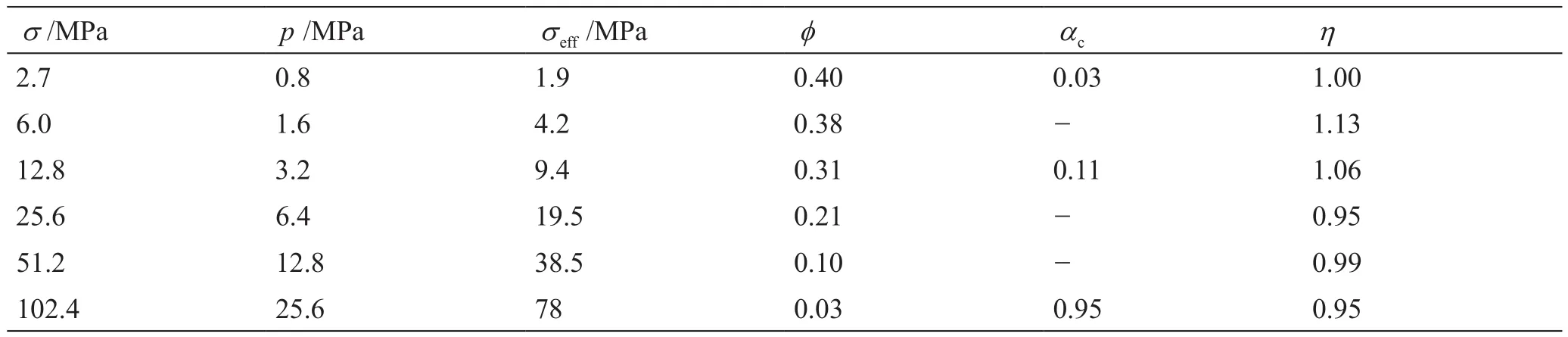
表1 铅粒高压测试结果Table 1 High pressure test results of lead shot

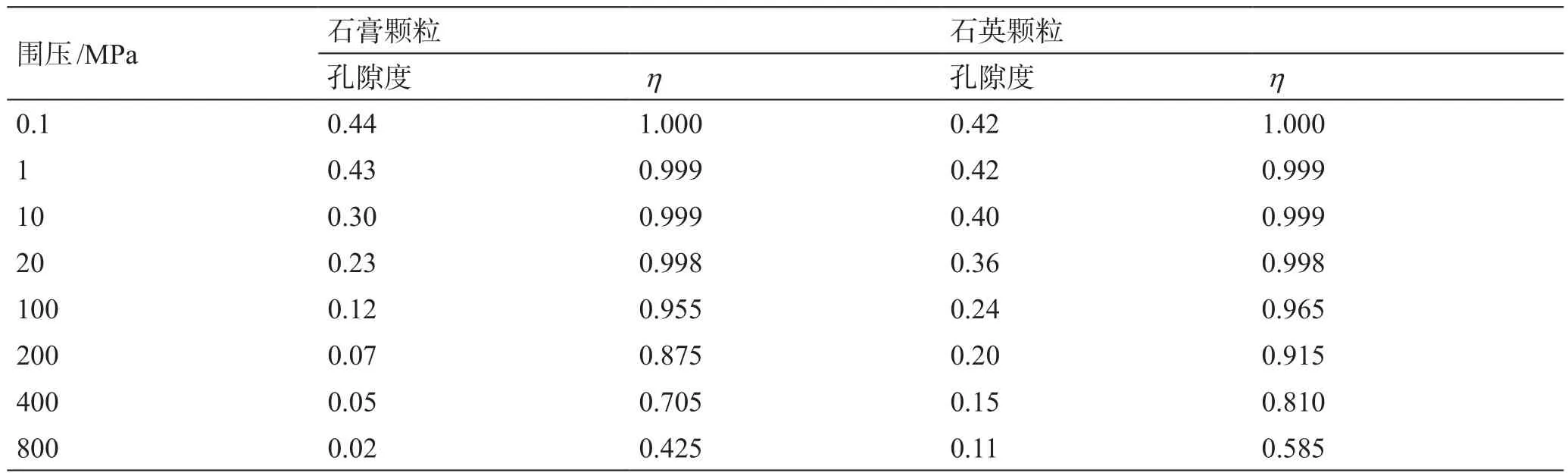
表2 石英和石膏颗粒高压测试结果Table 2 High pressure test results of quartz and gypsum grains

(2)1993 年Yamamuro[23]、1994 Bopp[24]石英颗粒和石膏颗粒高压实验

实验结果如表2所示。石膏颗粒在800 MPa由于形状变形较大可压缩孔隙度至0.02，石英颗粒在800 MPa孔隙度却仍大于0.1，石膏颗粒孔隙度下降较快的原因用新理论解释为石膏颗粒泊松比更大更易发生颗粒形状变形。此外，在20 MPa以内，两者的有效应力系数都几乎为1，其颗粒体积变形在低压可忽略不计，控制多孔介质变形的主要为引起颗粒间变形和颗粒形状变形的有效应力(σ-p)。而随着压力继续增大，颗粒体积变形影响不断增大，800 MPa时石膏颗粒体积变形达到57.5%，石英颗粒体积变形达到41.5%，则高压时需要综合考虑颗粒体积变形、颗粒形状变形和颗粒间变形。

(3)1933年Zisman[25]石英砂岩和大理石压缩实验

1933年Zisman[25]对石英砂岩和大理石分别进行了围压压缩系数测试实验，实验测试结果见图2。

从围压压缩系数图可知，随着围压增大，石英砂岩和大理石的压缩系数均下降且下降的速度越来越慢，这是因为：在低围压时岩石压缩系数远大于岩石颗粒压缩系数，主要为颗粒间变形和颗粒形状变形，随着压力不断增大，岩石压缩系数逐渐向颗粒矿物的压缩系数靠近。此外，大理石的组成矿物方解石相对石英砂岩的组成矿物石英更易形状变形，因此其初期压缩系数下降的幅度更大；而方解石的体积压缩系数1.34×10-5MPa-1相对石英2.7×10-5MPa-1也更小，最终大理石在高压下的压缩系数也比石英砂岩的压缩系数小。因此，岩石只有同时考虑颗粒间变形、颗粒形状变形和颗粒间变形才能解释和分析不同岩石的压缩系数变化规律。

常见岩土和颗粒的矿物压缩系数见表3所示。

一般情况下，岩石加围压后再降围压会有一部分体积变形不能恢复，这部分塑性变化损失掉的体积是由颗粒间变形造成的。而扣除这部分塑性变形的影响，只研究岩石弹性变形时，岩石弹性压缩系数超出颗粒压缩系数的那部分则为颗粒形状变形引起。从中可知，多数情况下，岩石总体积压缩系数大于颗粒体积压缩系数，岩石变形的机理为颗粒变形、颗粒形状变形和颗粒间变形综合作用，岩石颗粒间变形和颗粒形状变形不可忽略。旧双重有效应力研究岩石应变时只考虑颗粒体积变形从而严重低估了岩石体积应变和压缩系数大小。

图2 石英砂岩和大理石压缩系数Fig. 2 Compressibility of quartz sandstone and marble

表3 常见矿物颗粒和岩石的压缩系数表Table 3 Compressibility of common mineral particles and rocks

4 新理论应用举例

新双重有效应力和总有效应力方程可广泛应用于土力学、岩石力学等多孔介质力学中。本文重点举例其在油藏工程的应用，有效应力常被应用于岩石孔隙压缩系数和油藏应力敏感研究中。旧双重有效应力理论在研究岩石的孔隙压缩系数，仅以颗粒平均应力、颗粒体积变形为基础进行理论推导：

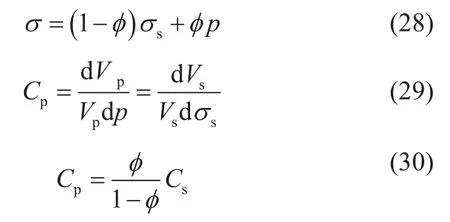
其中，Cp为孔隙压缩系数，Vp为孔隙体积，Vs颗粒体积。

基于上述理论推导，其得出了一些与实验矛盾的认识。其认为岩石孔隙压缩应为10-7～10-5MPa-1级别，而岩石颗粒压缩系数一般1×10-5MPa-1～3×10-5MPa-1，孔隙度0.02～0.35，实验室所测岩石孔隙压缩系数10-4～10-3MPa-1级别，其认识与实验所测存在较大偏差；基于方程(30)，其认为孔隙压缩系数与孔隙度成正相关，孔隙度越大，孔隙压缩系数越大、应力敏感程度越强，即认为高渗透储层的应力敏感程度大于低渗透储藏。而从前文分析可知，岩石孔隙体积变化主要由颗粒间变形和颗粒形状变形引起，颗粒体积变形引起的只是其中很小的一部分，未考虑颗粒间变形和颗粒变形是旧孔隙压缩系数理论计算值远小于实验测试结果的根本原因。基于新双重有效应力体系，恒总应力、变孔隙流压条件下的孔隙压缩系数理论推导如下：

根据方程(16)、(22)、(26)，在恒定总应力、变流压条件下，综合考虑颗粒体积变形、颗粒形状变形和颗粒间变形的总体积变化量ΔVb为：

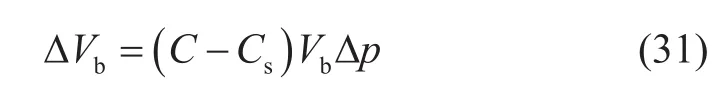
颗粒形状变形和颗粒间变形不影响颗粒体积变化，颗粒体积变化量ΔVs只跟颗粒体积变形有关，在恒总应力、变流压条件下，根据方程(18)有：

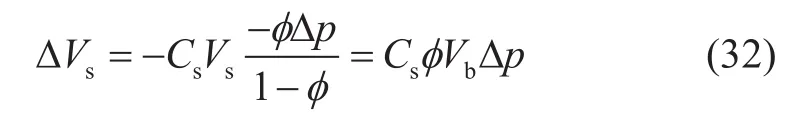
孔隙体积变化量ΔVp为总体积变化量与颗粒体积变化量之差，方程(31)减去方程(32)得：

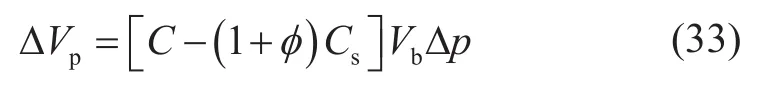
根据方程(33)，在恒定总应力、变流压条件下，综合考虑颗粒体积变形、形状变形和颗粒间变形的孔隙体积压缩系数Cp为：

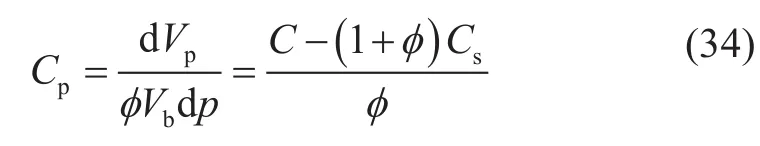
根据表3，岩石颗粒压缩系数一般1×10-5～3×10-5MPa-1，石英取 2.7×10-5MPa-1，孔隙度0.02～0.35，代入方程(34)，得到孔隙压缩系数理论值10-4～10-3MPa-1级别，这与实验测试范围一致。孔隙压缩系数理论计算式(34)所反应的规律与Hall[12]曲线图版的规律也一致，Hall图版如图3所示，孔隙压缩系数与孔隙度负相关，这是因为孔隙体积自身也是孔隙压缩系数的分母。基于新双重有效应力理论体系，一般储层渗透率越低，其孔隙压缩系数越大，其对应的储层应力敏感程度越高，理论计算与实验测试结果、Hall图版均一致。

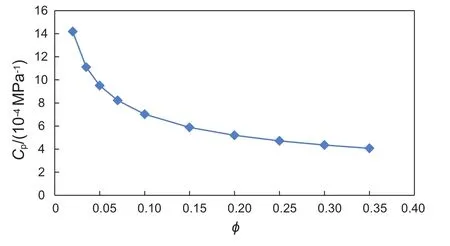
图3 Hall图版曲线Fig. 3 Hall Chart Curve

5 结论

(1)旧双重有效应力表达式与Biot、Bishop早期提出的有效应力表达式相同，与Laughton等高压实验认识相矛盾；新结构有效应力表达式与Terzaghi有效应力方程一致，其物理意义为超出平衡孔隙流压之外的颗粒间等效平均应力；新本体有效应力表达式综合考虑颗粒体积变形和颗粒形状变形，与颗粒等效平均应力、真实平均应力均不相等。

(2)新双重有效应力与Skempton有效应力内涵相同，其综合作用得到的总有效应力方程与Skempton有效应力方程一致。

(3)新双重有效应力首次提出了颗粒形状变形及其对岩石体积总变形的重大影响，未能考虑颗粒间变形和颗粒形状变形是李传亮孔隙压缩系数理论计算值远小于实验测试值的根本原因。

(4)新双重有效应力很好地解释了Laughton等经典实验测试结果，其推导出的新孔隙压缩系数与Hall图版认识一致，从应变机理上论证了岩石孔隙压缩系数与孔隙度负相关、低渗透油藏应力敏感程度更强的实验认识。研究成果为岩土工程等多孔介质力学以及油藏工程研究开启了新篇章。